Second Order Differential Evolution Algorithm

Xinchao Zhao, Guangzhi Xu, Dongyue Liu, and Xingquan Zuo

SecondOrderDifferentialEvolutionAlgorithm

Xinchao Zhao*, Guangzhi Xu, Dongyue Liu, and Xingquan Zuo

Differential evolution (DE) is a simple, efficient and robust Evolutionary Algorithm (EA) for various optimization problems, which has several outstanding features, such as low time complexity, ease to use and robust steadiness. So it is becoming more and more popular and being widely used in more and more applications. However, many questions are deserving to consider the balance between exploration and exploitation behaviors. The difference vector of mutation operator for the neighborhood and direction information has not been completely utilized. Therefore, a second order differential evolution algorithm, SODE, is proposed, which can efficiently utilize the search direction information from the second order difference vector. The optimal second order difference mechanisms are proposed for DE/rand/1 and DE/best/1 to utilize the neighborhood and direction information of the difference vector. Then it will guide the individuals toward the possible more encouraging areas. Extensive experiments and comprehensive comparisons show that the second order difference mechanism in SODE is much better than the classical first order difference mechanisms based mutation strategy-“DE/rand/1” and “DE/best/1” as far as the converging and steady performance.

differential evolution; second order difference vector; memory storage; swarm intelligence

1 Introduction

Many kinds of metaheuristic optimization algorithms are proposed for various increasing optimization problems in the recent few decades, which include Evolutionary Algorithms (EAs)[1], Particle Swarm Optimization (PSO)[2], Simulated Annealing (SA)[3], Ant Colony Optimization (ACO)[4]and Differential Evolution (DE)[5]etc.. Although these algorithms have better performance when solving various scientific and engineering problems involving nonlinear, multidimensional and no differentiable problems, many of them are still possible to be trapped in a local optimum when the current solution closes to the local trap or the optimal solution is far from the true optimum[6,7], especially for multimodal optimization problems[8].

Differential evolution, a simple, yet very efficient evolutionary algorithm for many complex optimization problems, was proposed by Price and Storn[5]. It has been proved that DE has a series of advantages, such as lower computational complexity, higher robustness and simplexes, which made it used to find the satisfactory or approximate solutions for optimization problems and real-world applications[9,10]. DE searches for optimal or satisfactory solutions with three operations: mutation, crossover and selection, in which mutation is the core operation of DE. In DE, the offspring is generated by perturbing the solutions with a scaled difference of selected population individuals followed by a crossover strategy. And DE has several control parameters such as population size (NP), the scaling factor (F) and crossover probability (CR).

However, the performance of classical DE algorithm is highly dependent on the mutation’s strategy and control parameter’s selection according to experimental studies[11]and theoretical analysis[12], which may lead to premature convergence and degradation of performance. Because basic and different vectors are randomly chosen from the current population, which does not utilize any neighborhood structure and/or beneficial direction information to guide the individuals toward the potential promising regions. This drawback will increase the possibility of being trapped in a local optimum when the current position is next to local trap or the optimal individual is far from the global optimum[13,14], especially for multimodal optimization problems[15].

Consequently, in order to apply DE successfully to solve the optimization problems and alleviate its disadvantages, various DE variants and a trial and error search for the strategies are proposed by many researchers and engineers. For example, Fan and Lampinen[16]proposed a trigonometric mutation operator to enhance the performance of DE algorithm. This modification enables the algorithm to get a better trade-off between convergence rate and robustness. Thus, it can be possible to increase the convergence speed and thereby obtain an acceptable solution with a lower number of objective function evaluations. Sun et al.[17]proposed a hybrid of DE and estimation of distribution algorithm, called DE/EDA. They designed DE algorithm from a new aspect, which utilized local information and global information respectively. The local information was obtained by modified mutation operation, while the global information was acquired from population’s solution by the proposed model. Three different learning strategies for conventional DE, one is for selecting the base vector and the other two are for constructing the difference vectors that were proposed by Wang and Xiang[18]. Zhao et al.[19]proposed a new hybrid differential evolution with simulated annealing and self-adaptive immune operation which introduced simulated annealing idea to escape from possible local optimum attraction. Lu et al.[20]combined corpus-based and Word Net-based similarity methods based on differential evolution algorithm and assessed semantic similarity between terms in a continuous vector space to improve similarity computation in terms of accuracy. Michael et al.[21]illustrated how the relative simple constrained multi-objective optimization algorithm Generalized Differential Evolution 3, can assist the practical sizing of mechatronic components used in e.g. digital displacement fluid power machinery. The robustness and convergence speed of the algorithm are investigated using different optimization control parameter settings and it is concluded that Generalized Differential Evolution 3 is a reliable optimization tool that can assist the mechatronic engineers in the design and decision making process. Shilpi and Karambir[22]implemented an optimizing technique called Differential Evolution to improve the effectiveness of test cases using Average Percentage of Fault Detection (APFD) metric. Wei Du et al.[23]proposed an Event-Triggered Impulsive (ETI) control scheme to improve the performance of DE. By introducing Impulsive control and event-triggered mechanism into DE, they hope to change the search performance of the population in a positive way after revising the positions of some individuals at certain moments.

In this paper, the second order differential evolution algorithm is proposed. What’s more, the optimal second order differential mechanisms are proposed for DE/rand/1 and DE/best/1. The major contributions of this paper are as follows:

• The second order difference vector mechanism is proposed: Introducing the second order difference vector which is based on the classical mutation strategy and analyze the effect of the proposed mechanism through the experiment.

• Different optimal second order differential mechanisms for DE/rand/1 and DE/best/1 is proposed: Two difference vectors of the second order difference vector are associated with each individual, which can be individually selected according to different classical mutation strategies.

This idea is powered by making use of the beneficial exploration direction of individual and employing different mutation strategies that support the production of new search moves that promote the detection of promising regions.

The rest of the paper is structured as follows. The basic concepts and formulations of differential evolution are described in Section 2. The proposed DE algorithm with new strategies is presented in Section 3. Section 4 presents the experimental results, analysis and evolutionary behavior comparisons. Finally, concluding remarks and future researches are summarized in Section 5.

2 Classical Differential Evolution

In this section, the basic operations of differential evolution will be introduced to better understand our new algorithm, which is proposed in Section 4. DE is an optimization algorithm based on the principles of natural evolution, using a population P with individuals encoded in floating point, as indicated in Eq.(1).

(1)

(2)

The four main steps in DE are initialization, mutation, crossover and selection.

2.1 Initialization

i=1,2,…,Np,j=1,2,…,D

(3)

2.2 Mutation operation

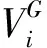
“DE/rand/1:”

Vi=Xr1+F(Xr2-Xr3)

(4)

“DE/best/1:”

Vi=Xbest+F(Xr2-Xr3)

(5)

“DE/best/2:”

Vi=Xbest+F(Xr2-Xr3)+F(Xr4-Xr5)

(6)

“DE/rand/2:”

Vi=Xr1+F(Xr2-Xr3)+F(Xr4-Xr5)

(7)

“DE/current-to-best/1:”

Vi=Xi+F(Xbest-Xi)+F(Xr2-Xr3)

(8)

“DE/rand-to-best/1:”

Vi=Xr1+F(Xbest-Xr1)+F(Xr2-Xr3)

(9)

wherei=1,2,…,Np,rk∈[1,Np],k=1,2,…,5,k≠i, are different random integers, and they are also different from vector indexi. The scaling parameterFis usually in [0.4, 1] and is used to adjust the exploration or exploitation step size. Eqs.(5&6) generate a new individual around the current best solution to exploit the current neighborhood. In order to enlarge the exploring region, Eqs.(7,8,9) provide two different vectors which are randomly selected to obtain a new solution. In this way, the population diversity can be maintained and more heuristic information can be utilized.

2.3 Crossover operation

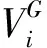
(10)

2.4 Selection operation

Selection operator contains a greedy mechanism according to their fitness of the trial vector and the parent individual. Then the better one, whose fitness is higher, is selected to survive for next generation. This operation is shown in Eq.(11) for minimization.

(11)

The above three operations repeat until the termination condition is met and a final solution is given.

3 SODE Algorithm

A novel second order differential evolution optimization algorithm, SODE, is proposed. The aim of proposing second order difference vector is to better utilize the search direction information. There is one word to say that, the motivation of this paper is not to propose a DE variant with powerful performance, but a distinct second order differential evolution algorithm model for the extensive subsequent research.

3.1Thesecondorderdifferencevectormechanism

Both classical mutation operations DE/rand/1 and DE/best/1 are used as the analytic generation strategies, which are the most successful and widely used schemes. Now, the beneficial heuristic direction information of the second order difference vector will be exploited. The second order difference vector information is indicated in Eqs.(12)-(16)， which are based on the two classical mutation strategies.

(12)

(13)

(14)

(15)

(16)

(17)

(18)

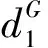
3.2AddthesecondorderdifferencevectortoDE/rand/1

The first component pattern ofdrGis made by Eqs.(14) and (15). The second component pattern ofdrGis made by Eqs.(13) and (15). In order to evaluate the performance of the proposed mechanism for DE/rand/1, a suit of benchmark functions[13] [20] [21]are selected as the test suit. The discussion on the performance of second order difference vector to DE/rand/1 will be presented in section 4.4.

3.3AddthesecondorderdifferencevectortoDE/best/1

The first component pattern ofdrGis made up by Eqs.(14&15). The second component pattern ofdrGis made up by Eqs.(13&15). In order to evaluate the performance of the proposed mechanism for DE/best/1, a suit of benchmark functions[13,20,21]are selected as the test suit. The discussion on the performance of second order difference vector to DE/best/1 will be presented in section 4.5.

4 Performance Comparison and Analysis

In order to discuss the performance of the proposed second difference strategy, 20 functions[13,20,21]with dimension 30 are used as the test suite and three DE variants are also adopted.

4.1 Benchmark functions

The test suit contains 6 unimodal functions and 14 multimodal functions. Functionsf1-f7, butf5, are unimodal functions, because Rosenbrock’s functionf5is a multimodal function when its dimension is larger than three.f8-f20are multimodal functions, and the number of local minima increases exponentially with the increase of problem dimension.f19is an unimodal, separable, scalable function.f20is a multi-modal, non-separable, scalable function. They are described in Table 1.

Table 1 Benchmark functions.

Continue table 1

4.2 Parameters setting

The parameters in this paper are as follows without the special situation.

• Number of independent runs: RUN=30

• Population size: SIZE=50

• Benchmark dimension: D=30 • Maximal iteration number: MAXFUNNUM=100000

Both parameters, scale factorFand crossover probabilityCRClassical DE are initialized to 0.5 for all the algorithms[22,23]. Parameterλis also simply initialized as 0.1 according to our experiments for parameterλ, which will be discussed in the next part.

4.3 Simulation results of parameter λ

The influence of the selection of parameterλwill be discussed in this section. The parameter ofλmay have an important influence on the population evolving for the current solutions. 5 unimodal functions(f1,f2,f3,f4,f6) and 3 multimodal functions(f5,f19,f20)are chosen to empirically analyze its effects. In order to achieve more reliable results and rule out other interference factors, the conventional parameters are set as 0.1, 0.3, 0.5, 0.7 and 0.9 respectively. Then the comparison ofλfor DE/best/1 among five different selections is plotted in Fig. 1 and indicated in Table 2. The comparison ofλfor DE/rand/1 among five different selections is plotted in Fig. 2 and summarized in Table 3.

Fig.1 indicates that parameterλfor DE/best/1 is very sensitive to the algorithmic performance. It can also be found that the evolving line ofλbeing 0.1 is located at the bottom of 6 functions for all 8 functions. At the same time, numerical results in Table 2 present the item comparisons for the parameterλ=0.1, 0.3, 0.5, 0.7 and 0.9 respectively. The first column gives the test functions for the experiments and the second column gives five different values ofλ. In order to clearly compare the results, the items of “min”, “median”, “mean” and “std” are presented, which are the minimal, median, average and standard deviation of all the final results in multiple runs. The experimental comparison in Table 2 clearly indicates that the algorithm withλ=0.1 performs best among all five choices for benchmark functions. Therefore, parameterλwill be chosen 0.1 in the following parts of the paper for DE/best/1.

Fig.2 indicates that parameterλfor DE/rand/1 is very sensitive to the algorithmic performance. It can also be found that the evolving line ofλbeing 0.1 is located at the bottom of 7 functions for all 8 functions. At the same time, numerical results in Table 3 present the item comparisons for the parameterλ=0.1, 0.3, 0.5, 0.7 and 0.9 respectively. The first column gives the test functions for the experiments and the second column gives five different values ofλ. In order to clearly compare the results, the items of “min”, “median”, “mean” and “std” are presented, which are the minimal, median, average and standard deviation of all the final results in multiple runs. The experimental comparison in Table 3 clearly indicates that the algorithm withλ=0.1 performs best among all five choices for benchmark functions. Therefore, parameterλwill be chosen 0.1 in the following parts of this paper for DE/rand/1.

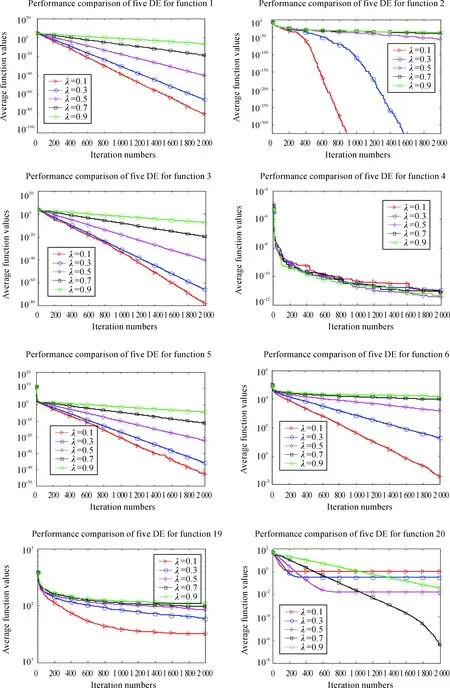
Fig.1 The comparative results of five parameters for DE/best/1.

λminmedianmeanstdf10．17．6280E-883．7454E-834．2049E-811．5281E-800．31．0475E-672．3247E-667．7773E-661．6136E-650．52．6880E-421．0036E-402．0878E-402．8538E-400．75．1106E-226．1659E-202．5106E-197．9992E-190．91．5754E-081．8418E-074．0466E-075．6518E-07f20．100000．300000．503．6999E-1454．2169E-582．1639E-570．71．3860E-667．2021E-441．9170E-396．5289E-390．91．4098E-432．8229E-398．2623E-374．3042E-36f30．14．5662E-872．3404E-835．4124E-792．6894E-780．32．6757E-691．9110E-678．4957E-671．6537E-660．51．1221E-438．1183E-425．3251E-411．1465E-400．71．0777E-224．2005E-211．3310E-201．8184E-200．94．7704E-092．9580E-083．4931E-082．5498E-08f40．12．7243E-155．9614E-129．4215E-129．8802E-120．34．2264E-152．1585E-121．0855E-111．6199E-110．53．2122E-151．5035E-123．7824E-127．7762E-120．72．7415E-151．3349E-127．0320E-121．8126E-110．91．1311E-141．0752E-124．2807E-127．8175E-12f50．12．2961E-488．0137E-461．6030E-434．0219E-430．31．2503E-371．1379E-361．8007E-362．1690E-360．55．2571E-248．1466E-231．0110E-229．9515E-230．75．9604E-133．4265E-124．6367E-124．0468E-120．91．1712E-052．8896E-053．2185E-051．7502E-05f60．12．9851E-032．1524E-023．5706E-024．0382E-020．31．8904E+001．1480E+011．8764E+011．7771E+010．53．8857E+021．2201E+031．5098E+039．6477E+020．73．3185E+038．5714E+039．1987E+033．2159E+030．98．3880E+031．5735E+041．5399E+043．1669E+03f190．11．8000E+013．1500E+013．1948E+017．8176E+000．33．0394E+016．2696E+015．9496E+011．4822E+010．56．6305E+018．7471E+018．5458E+011．0208E+010．77．4042E+019．7326E+019．6190E+011．1099E+010．98．4952E+011．0724E+021．0759E+021．0986E+01f200．11．0794E-034．4602E-019．2243E-011．0634E+000．301．9998E-022．9057E-015．4398E-010．5001．5462E-028．3828E-020．73．2024E-095．9876E-083．6123E-079．4670E-070．99．6550E-033．4770E-023．4410E-021．2583E-02

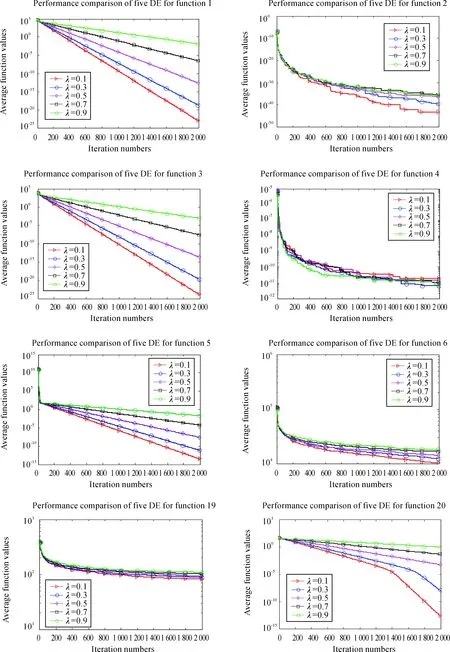
Fig.2 The comparative results of five parameters for DE/rand/1.

minmedianmeanstdf10．12．3748E-248．9364E-241．0791E-237．4357E-240．32．2481E-201．7031E-191．9115E-191．3418E-190．57．7264E-142．5173E-132．8213E-131．4254E-130．71．1364E-073．0378E-073．1974E-071．2165E-070．95．2271E-031．1470E-021．2312E-024．2024E-03f20．12．5920E-842．0303E-545．5454E-443．0339E-430．32．7092E-492．8089E-423．7573E-409．9621E-400．59．4267E-446．3708E-394．1188E-371．7745E-360．75．8460E-421．3581E-373．5245E-361．6267E-350．91．3643E-422．2592E-381．6980E-365．2681E-36f30．15．6101E-251．2114E-241．5209E-248．7373E-250．36．9903E-211．8458E-202．2353E-201．4554E-200．55．6471E-152．4238E-142．6119E-141．6640E-140．71．2183E-082．5242E-082．8771E-081．2787E-080．93．8878E-049．3069E-041．0003E-033．7333E-04f40．13．7035E-153．4163E-121．8382E-113．7888E-110．35．1973E-171．4428E-126．4210E-121．0733E-110．51．8682E-135．7236E-121．4242E-112．2713E-110．75．4746E-154．3894E-121．0482E-111．5998E-110．92．1840E-157．4248E-137．1842E-121．3502E-11f50．11．0619E-142．5203E-142．9253E-141．3661E-140．33．0948E-126．5844E-126．7447E-121．6803E-120．51．2988E-082．3529E-082．4017E-086．8930E-090．73．2190E-055．0411E-055．5018E-051．4460E-050．91．0708E-021．9155E-021．9515E-024．2629E-03f60．17．1855E+031．0725E+041．0462E+041．9158E+030．38．8619E+031．2352E+041．2469E+041．6214E+030．59．1152E+031．4289E+041．4252E+042．2462E+030．71．4035E+041．6941E+041．6884E+041．7970E+030．91．1992E+041．8700E+041．8360E+042．8819E+03f190．15．3188E+018．2814E+018．2523E+018．6160E+000．36．4938E+019．1962E+018．8314E+011．0019E+010．56．2106E+019．6627E+019．3259E+011．2688E+010．78．4442E+011．0173E+021．0276E+027．7944E+000．98．2279E+011．0524E+021．0671E+029．6852E+00f200．15．6843E-141．7764E-132．0440E-131．3113E-130．31．4024E-097．3160E-099．6733E-097．1346E-090．53．3792E-045．2640E-045．5936E-041．3135E-040．73．1780E-024．3001E-024．4544E-027．9437E-030．97．2583E-019．2463E-019．2312E-011．1465E-01

4.4SimulationresultsandcomparisonanalysisforDE/rand/1

In this paper, we propose the second order difference vector differential evolution. The new proposed algorithm is analyzed and verified with different algorithm variants and various benchmark functions.

(1) algorithms for comparison: In order to show the performance of the proposed algorithm, three DE algorithms are chosen to compare each other, and are described as follows:

• DE1: differential evolution using generation strategy “DE/rand/1”

• SODE11: adding the second order difference vector as Eqs.(14) (15) to differential evolution using generation strategy “DE/rand/1”.

• SODE12: adding the second order difference vector as Eqs.(13) (15) to differential evolution using generation strategy “DE/rand /1”.

(2) Results analysis and performance comparison:

All of the above algorithms are executed 30 independent runs on 20 functions. The final numeric comparison is presented in Table 4, which includes the items of Min, Median, Mean and STD in multiple runs. Observed from Table 4, it can be found that SODE11 and SODE12 algorithms outperform the classical DE1 algorithms. As the results shown, SODE11 performs best for 7 functions and SODE12 performs best for 9 functions for all functions. These results sufficiently indicate that the second order difference vector greatly benefits the search for the optimization process.

Table 4 Results of three algorithms for DE/rand/1.

functionItemDE1SODE11SODE12f6min000medi⁃an000mean000std000f7min1．1215E-027．3852E-034．6170E-03medi⁃an2．0762E-021．1231E-021．1918E-02mean2．0471E-021．1229E-021．1493E-02std4．5320E-032．2653E-033．0677E-03f8min2．1673E+0200medi⁃an4．2394E+031．3642E-111．3642E-11mean3．8753E+033．9479E+001．8596E-09std1．1944E+032．1624E+017．7577E-09f9min1．4425E+021．0046E+021．0216E+02medi⁃an1．8032E+021．1750E+021．1815E+02mean1．7831E+021．1711E+021．1711E+02std1．2415E+018．5869E+007．2292E+00f10min3．7434E-063．3129E-133．9879E-13medi⁃an7．9597E-067．1854E-136．8123E-13mean9．1488E-068．5674E-137．3369E-13std4．4827E-063．1726E-132．7606E-13

Continue table 4

functionItemDE1SODE11SODE12f16min-7．8332E+01-7．8332E+01-7．8332E+01medi⁃an-7．8332E+01-7．8332E+01-7．8332E+01mean-7．8332E+01-7．8332E+01-7．8332E+01std1．1574E-083．8332E-143．5108E-14f17min9．8575E+016．7058E+016．3962E+01medi⁃an1．5142E+028．5857E+018．0006E+01mean1．4583E+028．5083E+018．2750E+01std1．6545E+017．9043E+009．2737E+00f18min1．3254E-022．8422E-141．4211E-14medi⁃an2．1337E-021．4566E-131．5277E-13mean2．2176E-021．8143E-131．6366E-13std5．4823E-031．7485E-131．2841E-13f19min4．1448E-149．2787E-286．7387E-28medi⁃an1．9896E-132．9217E-273．1668E-27mean2．6145E-133．2166E-273．7943E-27std1．9673E-131．4735E-273．4331E-27f20min6．2181E-163．5249E-141．2903E-14medi⁃an5．0791E-115．9096E-111．8509E-11mean1．9275E-101．0588E-101．6550E-10std2．8449E-101．4707E-102．9653E-10

In general, SODE11 and SODE12 perform better than DE1 which indicates that the second order difference vector has a significant influence on the convergence ability and accuracy. The fact of SODE11 and SODE12 being better than DE1 indicates that the second order difference vector has a significant influence on the expansion of population’s diversity. These progressive phenomena verifies the excellent effects of the proposed second order difference information strategy.

(3) Online evolving performance comparison and analysis:

The online performance comparison among four DE algorithms is shown in Fig. 3, which further supports the previous numerical results and the related analysis. Observed from Fig. 3, SODE11 and SODE12 based on DE1 algorithm performs better for 16 from 20 benchmarks for the final results, except forf3,f5,f15,f16. The evolving lines of SODE11 and SODE12 decline faster than DE1 and they steadily obtain even better function values than the classical DE algorithms for all the functions. As the results shown, SODE11 performs best for 7 functions and SODE12 performs best for 9 functions for all functions. What’s more, it can be seen that DE1 suffers from frequent premature convergence for several functions significantly. In general, SODE11 and SODE12 present more robust performance and faster convergence speed when the second order difference information is considered, which shows the necessity and validity of the proposed strategy.

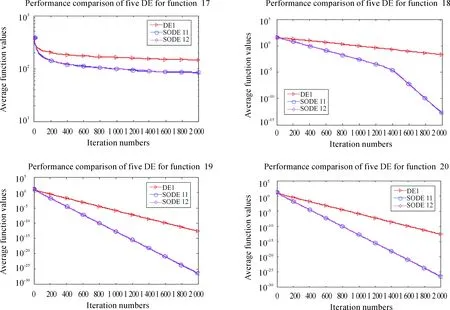
Fig.3 The comparative results of three algorithms for DE/rand/1.

4.5SimulationresultsandcomparisonanalysisforDE/best/1

(1) algorithms for comparison: In order to show the performance of the proposed algorithm, four DE algorithms are chosen to compare each other, which are described as follows:

• DE2: differential evolution using generation strategy “DE/best/1”

• SODE21: adding the second order difference vector as Eqs.(14) (15) to differential evolution using generation strategy “DE/best/1”.

• SODE22: adding the second order difference vector as Eqs.(13) (15) to differential evolution using generation strategy “DE/best/1”.

(2) Results analysis and performance comparison:

All of the above algorithms are executed 30 independent runs on 20 functions. The final numeric comparison is presented in Table 5, which includes the items of Min, Median, Mean and Std in multiple runs. Observed from Table 5, it can be found that SODE21 and SODE22 algorithms outperform the classical DE2 algorithms. As the results shown, SODE21 performs best for 15 functions and SODE22 performs best for 3 functions for all functions. These results sufficiently indicate that the second order difference vector greatly benefits the search for the optimization process.

In general, SODE21 and SODE22 perform better than DE2 which indicates that the second order difference vector has a significant influence on the convergence ability and accuracy. The fact of SODE21 and SODE22 being better than DE2 indicates that the second order difference vector has a significant influence on the expansion of population’s diversity. These progressive phenomena verify the excellent effects of the proposed second order difference information strategy.

Table 5 Results of three algorithms.

functionItemDE2SODE21SODE22f9min3．0844E+011．6914E+018．9546E+00medi⁃an4．8753E+012．7859E+012．3879E+01mean50．90882．8721E+012．4907E+01std14．71618．9859E+009．2249E+00f10min4．2419E-054．4409E-157．9936E-15medi⁃an2．6592E+009．3130E-011．3404E+00mean2．6462E+008．3009E-011．0513E+00std1．3577E+007．2911E-017．7577E-01f11min2．7850E-0900medi⁃an1．7235E-027．3960E-038．6267E-03mean4．6388E-021．0407E-022．3740E-02std7．6763E-021．4420E-024．0320E-02f12min1．7399E-051．5705E-321．5705E-32medi⁃an2．9201E+001．0367E-011．0367E-01mean3．9499E+004．6011E-013．0457E-01std4．1432E+009．2490E-014．4431E-01f13min1．0988E-021．3498E-321．3498E-32medi⁃an3．9747E+001．0987E-021．6006E-02mean5．7266E+006．7217E-016．8796E-01std5．8384E+001．0854E+001．2302E+00f14min-2．6750E+01-2．8102E+01-2．8405E+01medi⁃an-2．5150E+01-2．3511E+01-2．3859E+01mean-2．5104E+01-2．3378E+01-2．3943E+01std9．1336E-012．2108E+002．3589E+00f15min1．8645E+031．5039E+035．3399E+03medi⁃an1．6296E+041．0190E+041．6617E+04mean1．9935E+041．5895E+041．9065E+04std1．5947E+041．8682E+041．1499E+04f16min-7．2678E+01-7．5505E+01-7．5505E+01medi⁃an-6．8908E+01-7．1264E+01-7．0793E+01mean-6．8876E+01-7．1295E+01-7．1076E+01std2．5177E+002．2648E+002．6674E+00

Continue table 5

functionItemDE2SODE21SODE22f19min1．2313E-209．9433E-909．1163E-92medi⁃an6．8305E-121．0004E-862．8009E-84mean6．8196E-069．4213E-848．4675E-75std2．5980E-053．7331E-834．6378E-74f20min1．0139E-131．8771E-142．9769E-13medi⁃an1．9232E-113．6794E-113．6652E-11mean3．5644E-111．6194E-101．0081E-10std5．4285E-112．3891E-101．3582E-10

(3)Online evolving performance comparison and analysis:

The evolutionary performance comparison among several DE variants can be found in Fig. 4, which will further support the previous numerical comparison and the relative analysis. Observed from Fig. 4, SODE21 and SODE22 based on DE1 outperforms its competitors for 17 from 20 benchmarks for the final results. The evolulary curves of SODE21, SODE22 decline faster than DE2 and they steadily obtain even better function values than the classical DE algorithms for all the functions. As shown in the results, SODE21 performs best for 15 functions and SODE22 performs best for 3 functions. What’s more, it can be seen that DE1 suffers from frequent premature convergence for several functions significantly. In general, SODE21 and SODE22 present more robust performance and faster convergence speed when the second order difference information is considered, which shows the necessity and validity of the proposed strategy.

5 Conclusion and Future Work

In this paper, a novel DE variant, SODE, with the second order information of the difference vector, is proposed and investigated which expands the current research scope of the classical (first order) DE algorithms effectively. It is possible to efficiently utilize the second order direction information of difference vector and the beneficial population information for even better solution location and to enhance the adaptability of DE search mechanism. It is possible to spark even more interesting and challenging research topics in future. This strategy has distinct advantages on avoiding premature convergence. SODE is verified on some classic benchmark functions when compared with other DE algorithms. The simulation results indicate that its performance is very competitive and better than other classical algorithms. It also indicates the proposed strategies’ effectiveness and cooperation.

The better utilization of the second order information from the difference vector is an interesting topic for future research.

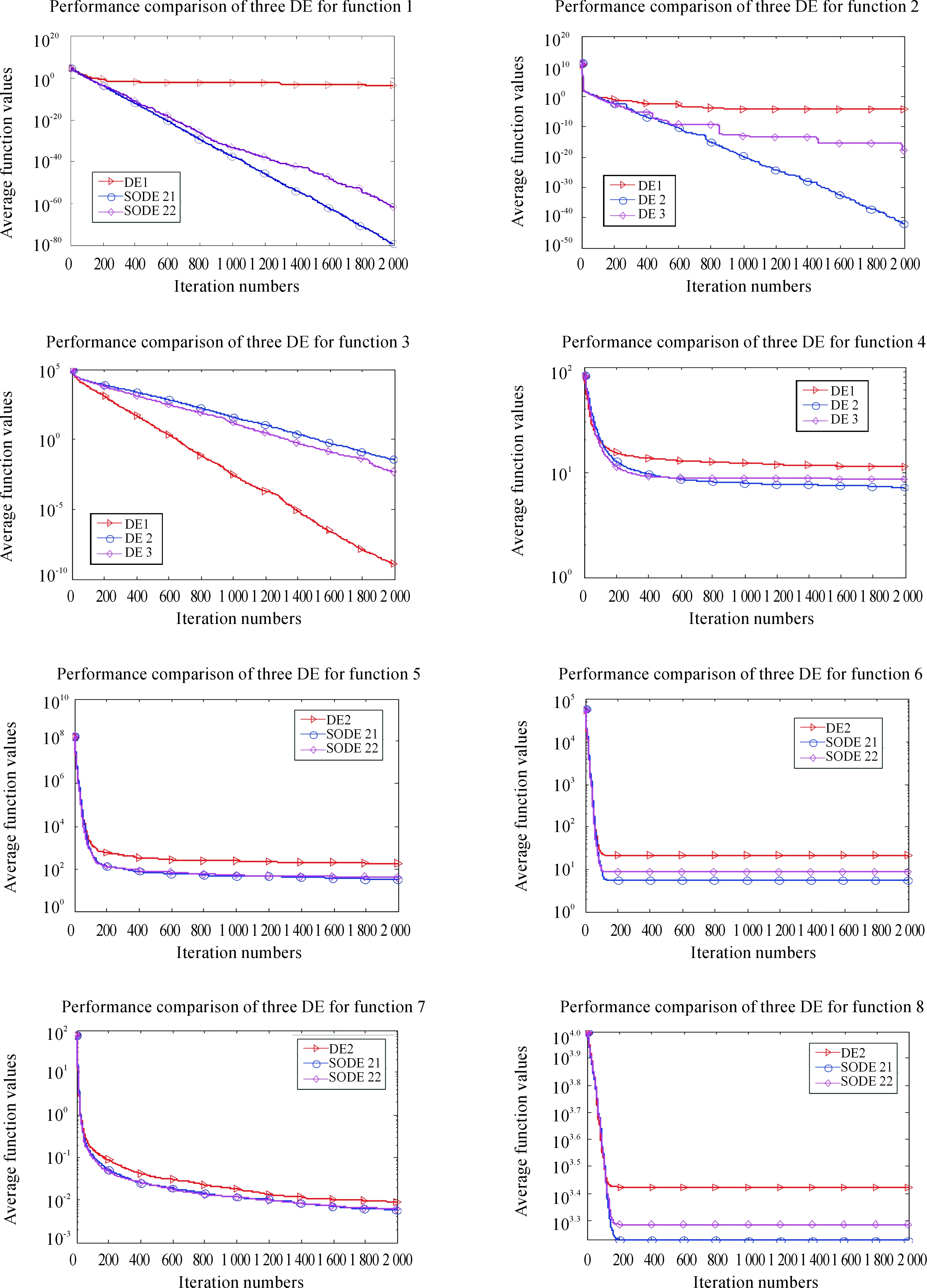
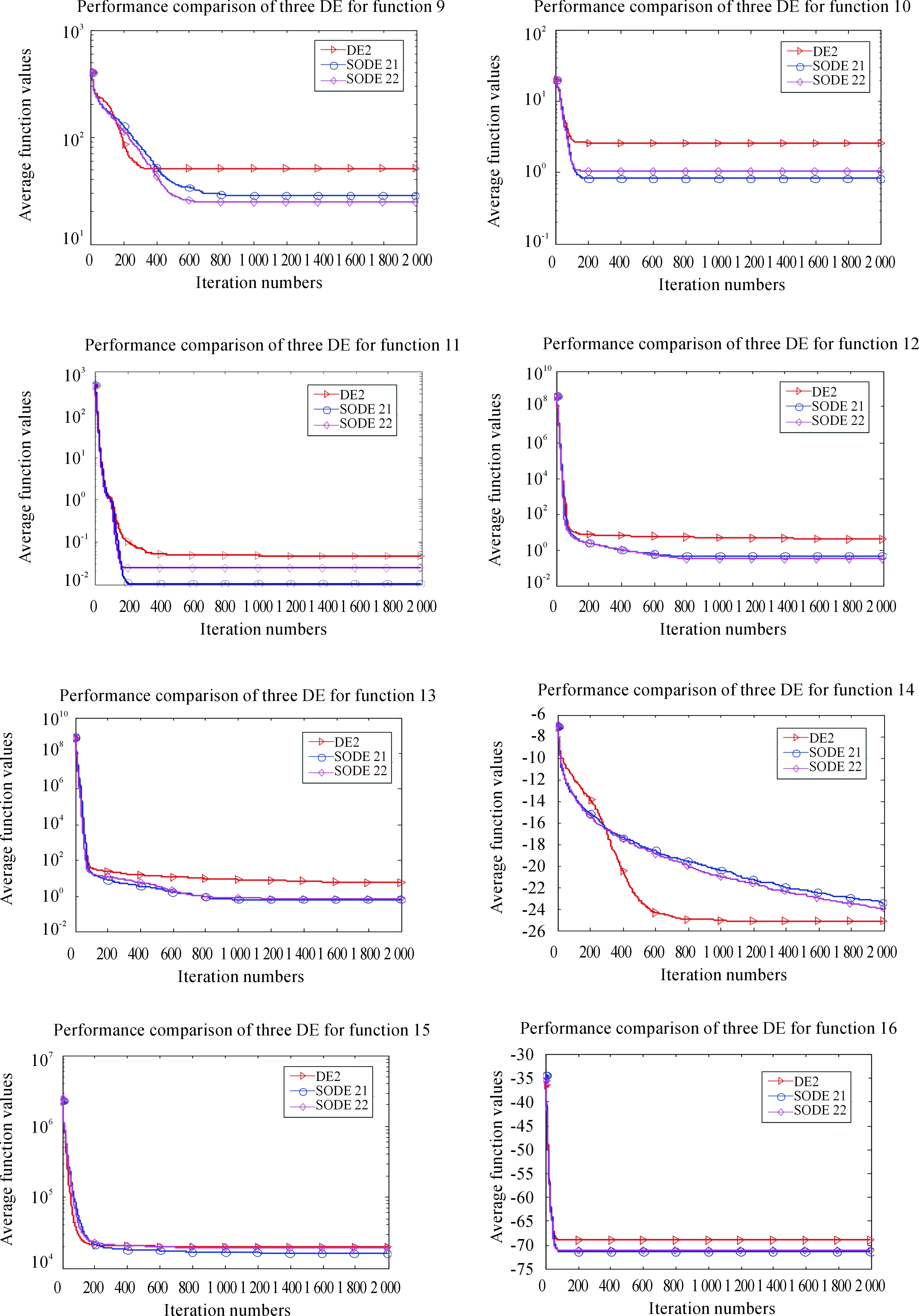
Fig.4 The comparative results of three algorithms for DE/best/1.

Acknowledgment

This research is supported by National Natural Science Foundation of China (61375066, 61374204). We will express our awfully thanks to our Swarm Intelligence Research Team of BeiYou University.

[1]T.Back, Evolutionary algorithms in theory and practice: evolution strategies, evolutionary programming, genetic algorithms, New York, USA:Oxford University Press, 1996.

[2]J.Kennedy, R.Poli, and T.Blackwell, Particle swarm optimization,SwarmIntelligence, vol.1,no.1, pp.33-57, 2007.

[3]S.Kirkpatrick, C.D.Gelatt, and M.P.Vecchi, Optimization by simulated annealing,Science, vol.220,no.4598.pp.671-680, 1983.

[4]M.Dorigo, V.Maniezzo, and A.Colorni, Ant system: optimization by a colony of cooperating agents,IEEETransactionsonSystems,Man,andCybernetics-PartB, vol.26,no.1,pp.29-41, 1996.

[5]R.Storn and K.Price, Differential evolution: A simple and efficient heuristic for global optimization over continuous spaces,JournalofGlobalOptimization, vol.11,no.4, pp.341-359, 1997.

[6]O.Hrstka and A.Kucerova, Improvement of real coded genetic algorithm based on differential operators preventing premature convergence,AdvancesinEngineeringSoftware, vol.35,no.3,pp.237-246, 2004.

[7]J.J.Liang, A.K.Qin, P.N.Suganthan, and S.Baskar, Comprehensive learning particle swarm optimizer for global optimization of multimodal functions,IEEETransactionsonEvolutionaryComputation, vol.10.no.3,pp.281-295, 2006.

[8]W.F.Sacco, N.Henderson, and A.C.Rios-Coelho, Topographical clearing differential evolution: A new method to solve multimodal optimization problems,ProgressinNuclearEnergy, vol.71,pp.269-278, 2014.

[9]Y.Wang, B.Li, and T.Weise, Estimation of distribution and differential evolution cooperation for large scale economic load dispatch optimization of powers systems,InformationSciences, vol.180,no.12, pp.2405-2420, 2010.

[10] M.Zhang, W.Luo, and X.Wang, Differential evolution with dynamic stochastic selection for constrained optimization,InformationSciences, vol.178,no.15,pp.3043-3074, 2008.

[11] K.Zielinski, P.Weitkemper, R.Laur, and K.D.Kammeyer, Parameter study for differential evolution using a power allocation problem including interference cancellation,InProceedingsofIEEEInternationalConferenceonEvolutionaryComputation,pp.1857-1864, 2009.

[12] J.Zhang and A.C.Sanderson, An approximate Gaussian model of differential evolution with spherical fitness functions, InProceedingsoftheIEEECongressonEvolutionaryComputation, Singapore, pp.2220-2228,2007.

[13] H.Y.Fan and J.Lampinen, A trigonometric mutation operation to differential evolution,JournalofGlobalOptimization, vol.27, no.1, pp.105-129, 2003.

[14] J.Y.Sun, Q.F.Zhang, and E.P.K.Tsang, DE/EDA: A new evolutionary algorithm for global optimization,InformationSciences, vol.169,no: 3-4, pp.249-262, 2005.

[15] Y.X.Wang and Q.L.Xiang, Exploring new learning strategies in differential evolution algorithm,IEEECongressonEvolutionaryComputation, pp.204-209, 2008.

[16] X.C.Zhao, W.Q.Lin, C.C.Yu, J.Chen, and S.G.Wang, A new hybrid differential evolution with simulated annealing and self-adaptive immune operation,ComputersandMathematicswithApplications, vol.66, no.10, pp.1948-1960, 2013.

[17] W.Lu, Y.Y.Cai, X.P.Chen, and K.L.Shi, Semantic similarity assessment using differential evolution algorithm in continuous vector space,JournalofVisualLanguagesandComputing, vol.31, pp.246-251, 2015.

[18] W.H.Wei, J.H.Wang, and M.Tao, Constrained differential evolution with multi-objective sorting mutation operators for constrained optimization,AppliedSoftComputing,vol.33, pp.207-222, 2015.

[19] J.Q.Zhang and A.C.Sanderson, JADE: Adaptive differential evolution with optional external archive,IEEETransactionsonEvolutionaryComputation, vol.13,no.5, pp.945-958, 2009.

[20] Y.W.Leung and Y.P.Wang, An orthogonal genetic algorithm with quantization for global numerical optimization,IEEETransactionsonEvolutionaryComputation, vol.5, no.1,pp.41-53, 2001.

[21] M.B.Michael, N.Christian, and B.Daniel, A global multi-objective optimization tool for design of mechatronic components using Generalized Differential Evolution, Inproceedingsof42ndAnnualConferenceoftheIEEEIndustrialElectronicsSociety, Florence, Italy: IEEE Press, pp.475-481,2016.

[22] Shilpi and Karambir, Improvising the effectiveness of test suites using differential evolution technique,Inproceedingsof5thInternationalConferenceonReliability,InfocomTechnologiesandOptimization, Noida, India: IEEE Press, pp.52-56, 2016.

[23] W.Du, S.Y.Leung, Y.Tang, A.V.Vasilakos, Differential Evolution with Event-Triggered Impulsive Control,IEEETransactionsonCybernetics, vol.47, no.1, pp.244-257, 2016.

GuangzhiXuwas born in 1987.He is a Ph.D.in Beijing University of Posts and Telecommunications.He has visited University of Glasgow as joined Ph.D.student.His research interests are Evolutionary computation and intelligent control, big data system and industry 4.0.

DongyueLiureceived the B.Sc. degree in Qilu normal university, Jinan, China, in 2014. She is currently working towards the M.Sc. degree in Swarm intelligence optimization from Beijing University of Posts and Telecommunications, Beijing, China. Her current research is focused on Differential evolution and global optimization.XingquanZuois currently an Associate Professor in Computer School, Beijing University of Posts and Telecommunications. He received the Ph.D. degree in control theory and control engineering from Harbin Institute of Technology, Harbin, China, in 2004. From 2004 to 2006, he was a Postdoctoral Research Fellow in Automation Department of Tsinghua University. From 2012 to 2013, he was a Visiting Scholar in Industrial and System Engineering Department, Auburn University, AL, USA. His research interests are in system optimization and scheduling, evolutionary computation, data mining with applications and intelligent transportation systems. He has published more than 70 research papers in journals and conferences, two books and several book chapters. He has led or participated in 20 research and industrial projects.

2016-12-20; revised: 2017-01-20

the Ph.D.degree in Applied Mathematics from the Chinese Academy of Sciences, Beijing, China, in 2005.He is currently with the School of Science, Beijing University of Posts and Telecommunications.His research interests include swarm intelligence, evolutionary computation, operations research and applications.

•Xinchao Zhao and Dongyue Liu are with School of Science, Beijing University of Posts and Telecommunications, Beijing 100876, China.E-mail: xcbupt@126.com.

•Guangzhi Xu is with School of Automation，Beijing University of Posts and Telecommunications, Beijing 100876, China. E-mail: xgzegw@gmail.com.

•Xingquan Zuo is with School of Computer Science，Beijing University of Posts and Telecommunications, Beijing 100876, China.

*To whom correspondence should be addressed. Manuscript