EGM-BP网络模型在单变量时间序列预测中的应用——以四川省GDP为例

刘 攀，冯长焕

（西华师范大学，四川 南充 637002）

EGM-BP网络模型在单变量时间序列预测中的应用
——以四川省GDP为例

刘 攀，冯长焕

（西华师范大学，四川 南充 637002）

利用GM(1,1)模型需要的数据少，而BP网络模拟精度高且适合非线性系统的特点，基于GM(1,1)模型的均值形式，以1980—2016年四川省GDP值作为原始序列，其累加序列、均值序列和前一历史序列作为输入向量，原始序列作为输出向量，进行BP网络训练，建立EGM-BP网络模型，提出了一种灰色神经网络的新方法。利用2014—2016年的GDP数据进行验证，发现EGM-BP模型对于单变量时间序列预测的精度比传统单一模型预测精度更高。

GM（1,1）模型；BP神经网络；单变量时间序列；GDP预测

0 引言

GDP（Gross Domestic Product）是指一个国家或地区所有常驻单位在一定时期内生产活动的最终市场价值。它反映了一个国家或地区一定时期内的经济实力和市场规模状况，是国民经济核算体系的核心指标。精准地预测GDP不仅能加强国家宏观调控，而且能促进企业经营管理，使得经济决策科学化。国内学者对GDP数据预测的研究成果颇多，建立的数学模型主要有回归模型、指数平滑模型、灰色GM（1，1）模型、ARIMA 模型、神经网络模型以及它们的组合模型[1-4]。

神经网络近年来在数学、物理、工程等领域的应用十分广泛，并涌现了大量的成果。BP网络是使用最广泛的一种神经网络，它通过建立从输入到输出的映射关系，在自动学习之后，能在一定条件下以任意精度实现任意的非线性映射。BP网络需要一定数量的训练样本才能作较好的预测。灰色GM（1，1）模型对数据的要求较少，但不能直接用于非齐次指数序列和振荡序列的建模。笔者把GM（1，1）模型和BP网络结合，建立EGM-BP网络模型，该模型同时具有GM（1，1）和BP网络的特点，能在较少信息量的情况下对未来时间序列作出较好的预测。

本文把1978—2016年四川省GDP值作为原始序列，利用灰色GM（1，1）模型中累加生成和均值生成的思想，生成与原始序列相关的3组序列，以此作为输入向量。把原始GDP值作为输出向量，构建了结构为3-6-12-1的BP网络。利用2014—2016年的GDP数据进行模型精度的比较，结果表明EGMBP网络模型比传统单一模型误差更小，精度更高。

1 模型的原理和方法

1.1 EGM（1，1）模型

灰色系统理论由邓聚龙教授在1982年创立，目前已被广泛应用于自然科学、社会科学、工程技术等各个领域。GM（1，1）模型是灰色系统理论的核心部分，它有4种基本形式：均值形式（EGM）、原始差分形式（ODGM）、均值差分形式（EDGM）和离散形式（DGM）。人们提到的 GM（1，1）模型通常是指EGM（1，1）[5]。EGM（1，1）通过建立关于原始序列的特殊差分方程和微分方程，在一定程度上模拟单变量时间序列，能对未来时间序列做出预测。

EGM（1，1）的建模步骤如下：

设原始序列 X ( 0) = (x (1),x (2),⋅⋅⋅,x (n ))，x（0）（k）≥0，k=1，2，…，n。记 X（0）的累加序列为 X（1）=（x（1（）1），x（1）（2），…，x（1）（n）），记X（1）的紧邻均值序列为Z（1）=（z（1）（1），z（1）（2），…，

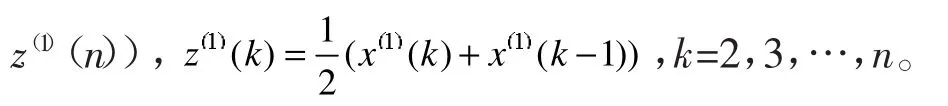
（1）建立白化微分方程：

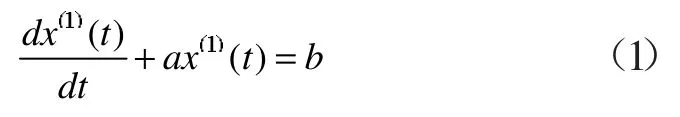
其中a，b满足差分方程：

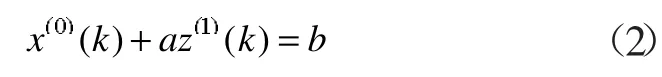
称 a 为发展系数，b 为灰色作用量，z（1）（k）为灰色背景值。

（2）利用最小二乘法求参数向量 a^ = [a, b]=（BTB）-1BTY，其中 BT，Y 分别为：

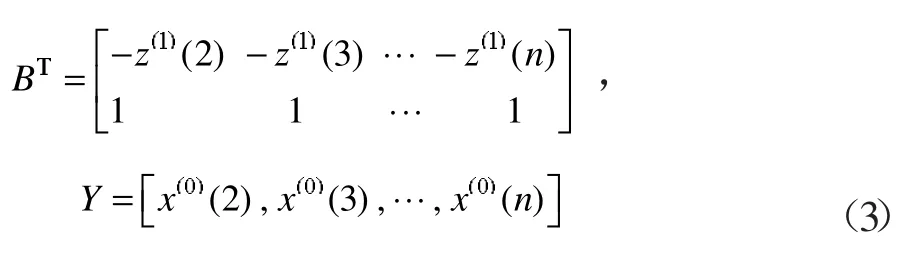
得到白化微分方程的解（也叫EGM（1，1）模型的时间响应式）：

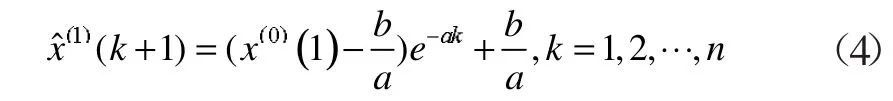
（3）求累减还原式，得到原始序列的模拟表达式：

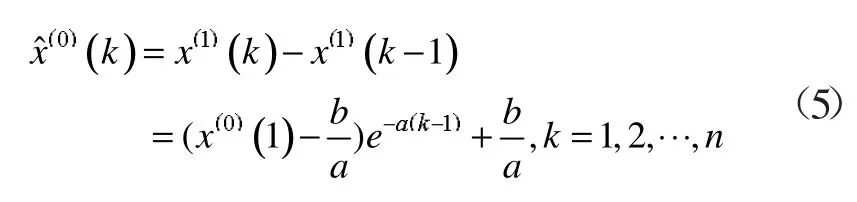
1.2 BP网络模型

BP网络(Back-Propagation Network)，即反向传播网络，由Rumelhart等人在1986提出，是目前使用最广泛的神经网络模型[6]。BP网络在函数逼近、模式识别、数据的压缩与分类等方面得到了大量的应用。

其模型的思想为：建立一个三层或三层以上的神经网络（输入层、隐层和输出层），使数据从输入层向隐层传输，隐层向输出层传输。层与层之间由激励函数和权值连接，在数据传输的过程中，通过误差的反馈，不断地反向调整各层之间的连接权值，直至达到指定的精度或运算次数。

MATLAB软件构建BP网络的步骤[6，7]：

（1）网络结构的设置

BP网络结构由输入层、隐层和输出层构成，隐层至少为一层。根据Kolmogorov定理，一个三层的前馈神经网络能以任意精度逼近任意连续的函数[7]。随着网络层数的增加，误差进一步降低。但这也会增加网络的复杂性和学习时间。所以，一般不增加网络的层数，而是通过增加隐层神经元的个数来尝试降低误差，提高精度。

（2）输入层和输出层的设置

输入向量为影响待预测序列的主要因素序列，输入层节点为主要因素的个数。输出向量为需要预测的序列，其节点数为待预测序列的个数。为了消除量纲的影响以及提高网络学习的收敛性，通常需要对数据作归一化处理，把数据规范在[-1,1]或[0,1]区间内。

（3）隐层节点的设置

目前，关于隐层节点的设置还没有一个具体的公式来确定，一般使用试凑法及以下经验公式[6]来确定：

3） N = l ogn ，其中n为输入层节点数。

（4）网络参数的设置

在MATLAB中，使用newff函数创建一个BP网络。层与层之间的激励函数主要有S型对数函数(logsig)、S型正切函数(tansig)和纯线性函数(purelin)等。BP网络训练函数默认为L-M算法训练函数(trainlm)。期望误差的学习目标默认为0，可以根据需要设置学习目标的精度。迭代次数一般不超过50000次。学习效率在0到1之间，并不是越大或越小越好，太大使系统不稳定，太小会使训练时间过长。

（5）网络训练与检验

（6）预测与误差分析

1.3 EGM-BP网络模型

（一）EGM-BP网络模型的原理

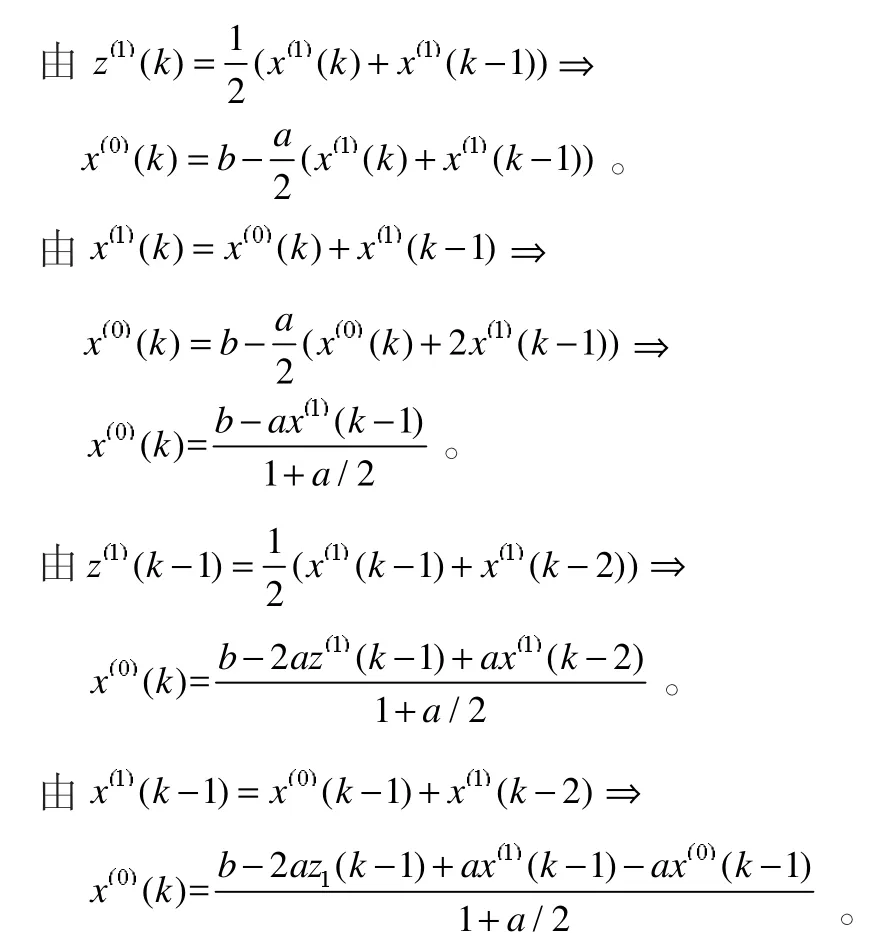
（二）EGM-BP网络模型主要步骤

（1）设原始序列 X（0）=（x（0）（1），x（0）（2），…，x（0）（n））,X（0）（k）≥0，k=1，2，…，n；

（2）计算X（0）的前一历史序列X'（0）、累加序列 X（1）、以及 X（1）的紧邻均值序列为 Z（1）；

（3）把X'（0）、X（1）、Z（1）作为输入向量，X（0）作为输出向量，构建BP网络；

（4）网络训练与检验；

（5）预测与误差分析。

2 实证分析

2.1 数据的选取

本文选取1978—2016年四川省GDP数据为研究对象（单位为亿元），数据来源于四川统计局。以2014—2016年的数据作为检验数据。

记1980—2016年的原始GDP值为输出向量T0=［t（1），t（2），…，t（37）］。分别记T0的累加序列、累加序列的均值序列、前一历史序列为pi（i=1，2，3），记输入向量 p0=［p1；p2；p3］。

2.2 EGM-BP网络模型步骤

（1）网络结构、输入层和输出层的设置

本文选择建立四层BP网络，由T0和P0知，输入和输出层节点分别为3和1。由于S型激励函数的输出值只能无限接近0或者1，而不能达到0或者1，为了增强网络的泛化能力，本文把数据规范在[0.1,0.9]区间内。归一化的方法是其中M和m分别为该序列的最大值和最小值。

（2）隐层节点的设置

本文采用试凑法，得出适合的两个隐层节点数分别为6和12，相应的BP网络结构为3-6-12-1。

（3）网络参数的设置

通过反复试验，得到适合的网络参数见表1。其他参数选择MATLAB默认设置。

表1 EGM-BP网络模型参数设置

（4）网络训练

（5）网络的检验与预测

利用2014—2016年四川省GDP数据对模型进行精度检验，结果见表2。结果显示，预测值与实际值的相对误差的绝对值都在0.3%以内，误差较小。

2017年四川省GDP的前一历史值为32680.5亿元，累积值为284519.71亿元，累加值的均值生成为268179.46亿元。把这三个值作为输入向量，得到2017年四川省GDP的预测值为35008.87亿元。相对2016年的增速约为7.12%，与四川省2017年1季度GDP实际增长接近。

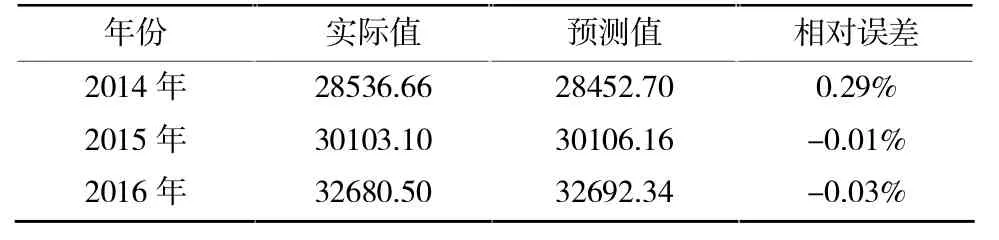
表2 EGM-BP网络模型检验结果

3 其他模型结果的对比

3.1 基于时间的曲线拟合模型

记1980—2013年四川省GDP值为y，时间t=1，2，…，34。分别对y关于t作一次曲线、二次曲线、三次曲线拟合，结果显示三次曲线的拟合度最高，为0.991。拟合曲线为：

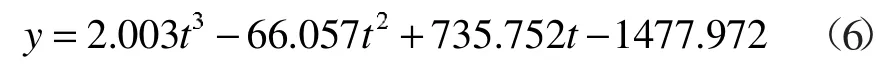
由于1980—2013年四川省GDP呈近指数增长，分别对y关于t作S型曲线、生长曲线拟合，生长曲线的拟合度最高为0.995。拟合曲线为：

3.2 GM（1,1）模型

由于旧信息历史久远，与新信息的相关程度可能不高，新信息显得更重要，因此建立灰色新陈代谢模型。分别建立4至10阶GM（1，1）模型，结果表明，4阶GM（1，1）模型的误差最小，其结果见表3和表4。

3.3 BP网络模型

针对1980—2013年四川省GDP数据，把年份作为输入向量，原始GDP作为输出向量，建立BP网络，结果见表3和表4。

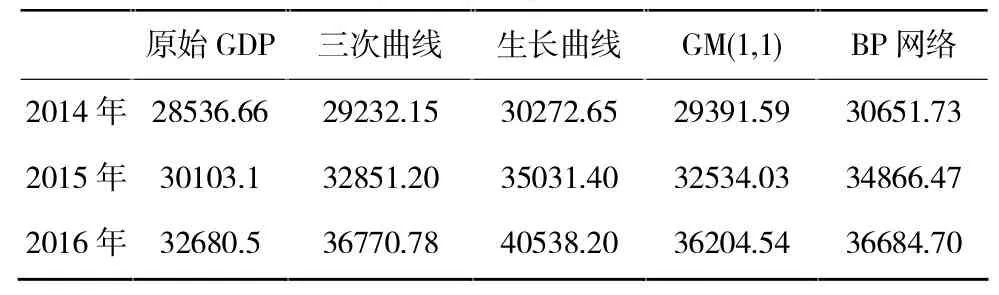
表3 传统单一模型预测结果

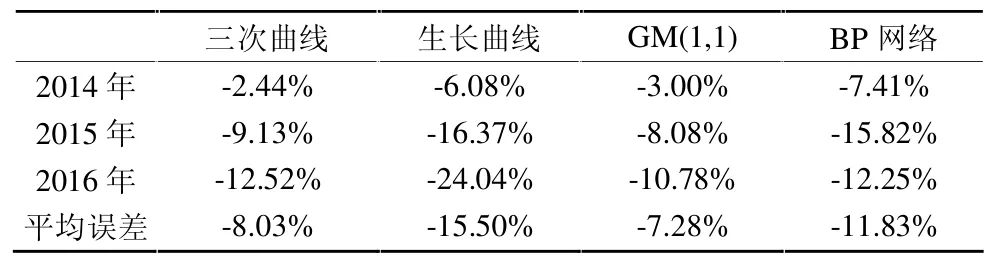
表4 传统单一模型预测相对误差

4 结语

四川省作为西部人口大省，科学地预测其GDP总量对于政府制定经济政策和企业规划有重要的意义和价值。预测结果表明2017年四川省GDP总量将持续增加，增长率将在7.12%左右。基于GM（1，1）模型的累加生成和均值生成的思想，结合BP网络，本文建立了EGM-BP网络模型，实验结果表明，EGM-BP模型比传统单一模型效果更好，精度更高。本文提出的EGM-BP模型还可用于其他单变量时间序列的预测。另外，人工神经网络中其他网络也具有良好的预测功能，如RBF网络、Elman网络、小波神经网络等，后续研究可考虑将累加生成和均值生成的思想与这些网络结合进行科学预测。

［1］龙会典，严广乐.基于 SARIMA、GM（1，1）和 BP 神经网络集成模型的GDP时间序列预测研究［J］.数理统计与管理，2013，32（5）:814-822.

［2］许金炜.基于虚拟变量回归与SARIMA组合模型的GDP预测［J］.统计与决策，2016，（24）:38-41.

［3］薛倩,牟凤云,涂植凤.组合预测方法在重庆市 GDP预测中的应用 ［J］.重庆工商大学学报 （自然科学版），2017，34（1）:56-63.

［4］龙会典,严广乐.基于改进的 GM（1，1）-Markov链组合模型广东省单位GDP能耗预测［J］.数理统计与管理，2017，36（2）:200-207.

［5］刘思峰，谢乃明，等.灰色系统理论及其应用（第六版）［M］.北京：科学出版社，2013:97-121.

［6］飞思科技产品研发中心.神经网络理论与MATLAB7实现［M］.北京：电子工业出版社，2005:99-107.

［7］施彦，韩力群，廉小亲.神经网络设计方法与实例分析［M］.北京：北京邮电大学出版社，2009:23-36.

EGM-BP Network Model in the Application of Single Variable Time Series Prediction——Taking Sichuan GDP as Example

LIU Pan,FENG Chang-huan
（China West Normal University，Nanchong 637002,China）

GM(1,1)model requires less data and BP network modeling is of high accuracy and suitable for the nonlinear systems.Thus，based on EGM(1,1)model，the GDP value of Sichuan Province from 1980 to 2016 was set as the original series,then its cumulative series，average series and the series of previous historical period was set as input vector，and the original series was set as the output vector to conduct the BP network training.EGM-BP network model was set up，proposed a new method for gray neural network.In the 2014-2016 GDP data verification，the results showed that EGM-BP model for single variable time series had higher precision than traditional single model.

GM(1,1)；BP neural network；single variable time series；GDP forecast

F224

A

1674-3229（2017）03-0008-04

2017-06-03

西华师范大学基本科研项目(14C004)；南充市社科规划一般规划项目（NC2013B027)

刘攀(1995-)，男，西华师范大学硕士研究生，研究方向：应用数理统计；冯长焕（1972-），女，硕士，西华师范大学数学与信息学院教授，研究方向：应用数理统计。