基于系统动力学的连锁零售多级库存优化与仿真

赵 川，张 浩

（北京工商大学商学院，北京市100048）

基于系统动力学的连锁零售多级库存优化与仿真

赵 川，张 浩

（北京工商大学商学院，北京市100048）

连锁零售企业多级库存系统中各节点存在着由于需求预测不准确、订货时间随意、订货量缺乏动态时变性等因素而导致的总体库存量高于理想水平、库存周转率低下、库存成本过高等问题。为解决此类问题，可从动态系统的角度构建由供应商、配送中心和门店组成的多级库存协同管理系统动力学模型，以超市发连锁零售门店的进销存数据为实证数据，应用Vensim平台对模型进行仿真研究。通过敏感性分析对库存调节周期、配送时间、需求预测权重、安全库存天数等参数进行改进，最终得到一个优化的连锁零售多级库存系统动力学模型。实验结果表明，该模型能够有效降低企业库存量，提高库存周转效率，降低库存成本。

系统动力学；连锁零售；多级库存优化

一、引言

库存管理是连锁零售企业运营管理中重要的一环，库存成本的高低直接影响着连锁零售企业的经济效益。目前我国连锁零售企业的多级库存管理存在着包括因销售量波动大导致的库存量居高不下、订货时间随意、库存周转时间长、库存周转效率低等问题[1-3]，库存成本在连锁零售企业运行费用中仍然占有很高的比例。连锁零售企业多级库存具有明显的非线性、多环路、动态性、延迟性等复杂动力学特征，而系统动力学擅长处理高阶复杂、多环路、非线性及时间延迟的动态问题，因此系统动力学具有应用于库存控制领域的基础条件，有助于解决连锁零售企业的多级库存管理问题[4-5]。

二、文献及理论分析

在供应链库存控制领域的系统动力学应用中，不同学者从不同角度进行了大量的研究。福瑞斯特（Forrest）[6]基于系统动力学原理，分析了消费需求波动沿供应链向上游企业逐级放大的系统特性，并分别分析了因决策延迟、需求波动、随机噪声、生产能力限制、广告等因素对库存的影响。多维尔（Towill）[7]在系统动力学基础上建立了著名的库存—订货控制系统（IOBPCS），解决了由需求波动引起的库存量增加等一系列问题。波勒斯（Poles）[8]从再制造供应链角度建立了生产和库存的系统动力学模型，分析和研究了库存量、交货时间等因素对系统的影响，比较了生产提前期和再制造提前期对系统的影响，并通过案例进行了验证。巴拉吉和詹姆斯（Balaji&James）[9]研究并建立了一个包含供应商和制造商的协同式供应链库存管理（CPFR）系统动力学模型，通过比较不同随机需求下该模型的供应链绩效，验证了协同式供应链库存管理的优化性能。

在国内学者中，张力菠、韩玉启等[10]在总结系统动力学的理论研究与应用发展的基础上，根据供应链管理相关问题的分类，指出了在供应链管理领域中系统动力学的应用方向。廖诺、张毕西、吴小结[11]建立了一个供应链节点企业的系统动力学模型，通过比较不同外部需求条件下模型的动态性能，提出了供应链优化的方案。汪小京、刘志学、徐娟[12]将第三方物流（TPL）引入供应商管理库存模型（VMI）中，建立了第三方物流管理库存（TMI）的系统动力学模型，通过仿真分析认为在需求相同的情况下，TMI比VMI能够进一步降低系统库存水平。成琼文和周璐[13]则从绿色供应链角度，从采购、库存、设计和管理四个方面建立了绿色供应链管理的系统动力学模型，实证研究了绿色供应链管理实践的因素相互关系和影响路径。以上文献主要在传统供应链的采购、生产、配送等环节运用系统动力学研究库存管理问题，但在连锁零售供应链多级库存方面的系统动力学研究还比较缺乏。本文在系统动力学的理论基础上，结合连锁零售企业多级库存网络化、连锁性、订货批量小、交易频繁和需求变化大的特点，考虑连锁零售企业多级库存管理系统中供应商、配送中心和门店库存信息流的内在因果关系，构造一个动态库存管理模型，并通过敏感性实验对模型进行了优化，力争为连锁零售企业多级库存管理提供决策依据。

三、多级库存系统动力学建模

（一）建模思想与假设

本文要建立的库存管理模型涵盖连锁零售企业的供应商、配送中心和门店三级库存管理系统，涉及以下相关决策要素：在供应商方面，包括发货量和送货时间；在配送中心方面，包括实际库存量、期望库存量、库存偏差、订货量、库存调节周期、配送时间、安全库存天数、收货量以及发货量；在门店方面，包括实际库存量、期望库存量、库存偏差、订货量、库存调节周期、收货量、发货量以及销售量。

为了更好地再现系统的内部结构、要素之间的相互关系及其动态相关行为模式，本文提出了系统动力学模型如下假设：

H1：供应商提供的商品合格率为100%，不考虑退货问题；

H2：供应商发货到配送中心、配送中心发货到门店需要一定的前置时间；

H3：不考虑连锁零售库存管理系统的采购、销售、运输、存储能力限制；

H4：供应商可按下游需要随时向配送中心提供任意数量的商品，不存在缺货问题。

（二）模型因果关系及变量的设定

对中小型连锁零售库存管理系统而言，如果门店销售量增加，则门店库存量减少，进而导致门店库存偏差增加；门店期望库存量越大，则门店库存偏差也越大；门店库存偏差增加将直接导致门店订货量增加，进而使配送中心发货量相应增加；配送中心发货量增加，使在途库存量I（配送中心至门店的在途库存量）增加，最终经过门店收货，在途库存变为门店库存量也相应增加。在此因果反馈回路中，门店库存量的减少会最终导致门店库存量增加。因此，该反馈回路是负因果反馈回路，具有内部调节和稳定库存的作用。

同样，配送中心发货量的增加直接导致配送中心库存量减少，进而使配送中心的库存偏差增加；配送中心期望库存量的增加也使配送中心库存偏差增加；而配送中心库存偏差越大，则配送中心的订货量就越大，进而导致供应商发货量的增加；在途库存量II（供应商至配送中心的在途库存量）直接受到供应商发货量的影响，随之增加；当在途库存量II转变成配送中心库存量时，配送中心的库存量也相应增加。在此因果反馈回路中，配送中心库存量减少，会最终使配送中心库存量增加。因此，该反馈回路是负因果反馈回路，具有内部调节和稳定库存的作用。

根据上述分析并结合前述对系统要素的界定，可以得到中小型连锁零售库存管理系统的因果关系图（参见图1），模型中的状态变量参见表1。

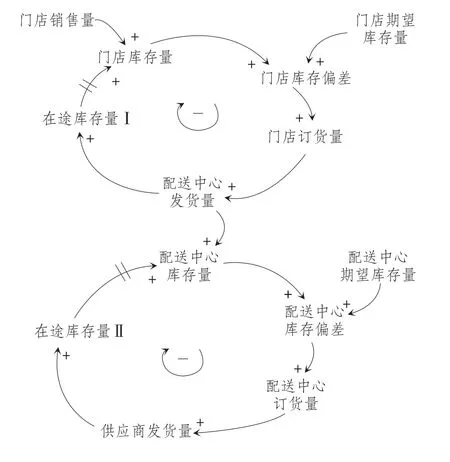
图1 连锁零售库存管理模型的因果关系

根据以上分析，在构建了连锁零售企业多级库存管理因果关系的基础上，进一步确定变量的类型和性质，建立连锁零售库存管理系统动力学流程图（参见图2）。

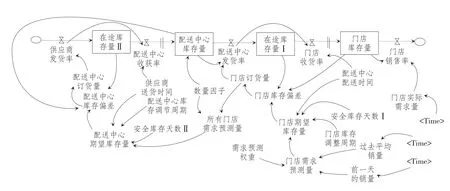
图2 连锁零售库存管理系统的总流程

（三）模型的主要方程体系

本文应用Vensim仿真平台提供的各函数表示变量间的关系：L表示状态变量方程，R表示速率变量方程，A表示辅助变量方程，C表示常量方程。其中速率变量方程的作用是把来自系统内外诸多影响系统状态的因素转化为改变系统状态的行动，而辅助变量方程的作用是描述系统中重要的信息量，并据此建立速率方程。本文建立模型相关的方程如表2所示。其中，延迟时间I是配送中心库存调节时间，是从配送中心发货到门店收到货物形成门店库存量所需的时间；延迟时间II是供应商送货时间，是从供应商发货到配送中心收到货物形成配送中心库存所需的时间；数量因子是系统中门店的数量。

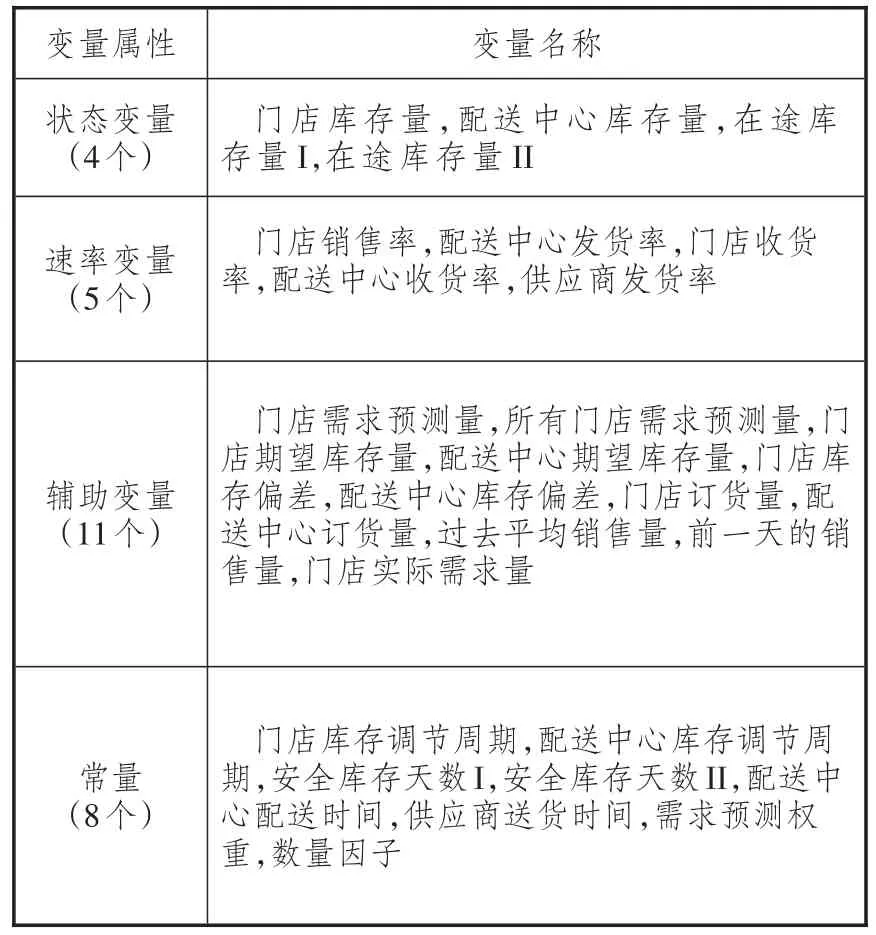
表1 模型变量汇总

四、数值仿真及分析

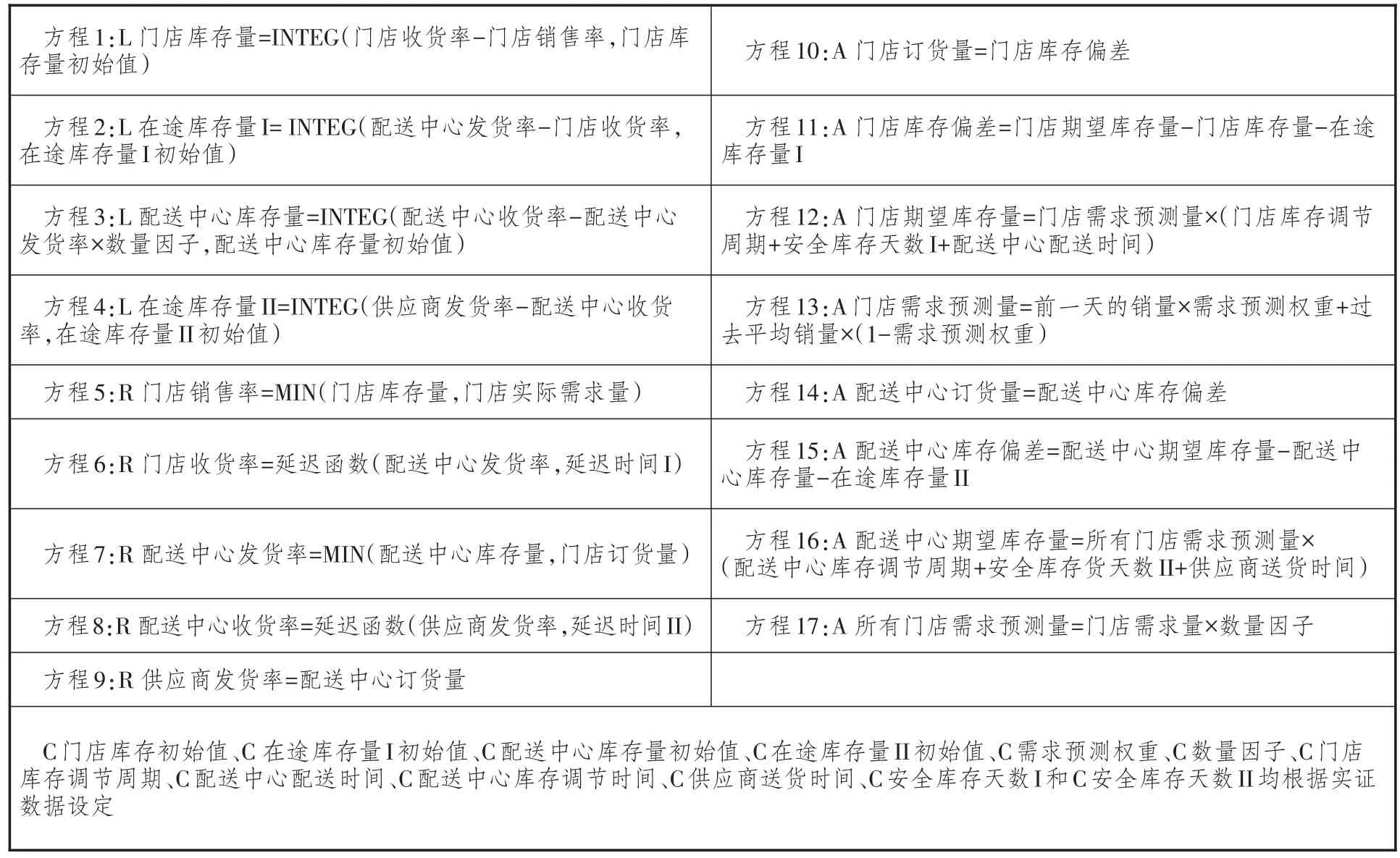
表2 库存系统动力学模型的主要方程关系

（一）模型的仿真

本文选用北京超市发连锁零售某门店食用油1个季度的销售、库存和订货数据作为实验数据，该商品在该季度的日销售量存在一定波动，平均销售量为2.5桶/天。门店订货量不规律，订货量忽高忽低，订货时间较随意，且该商品平均库存量大约为80桶/天，库存周转期为31.86天。由该门店的相关经营数据可以确定模型中各主要变量的初始值（参见表3）。

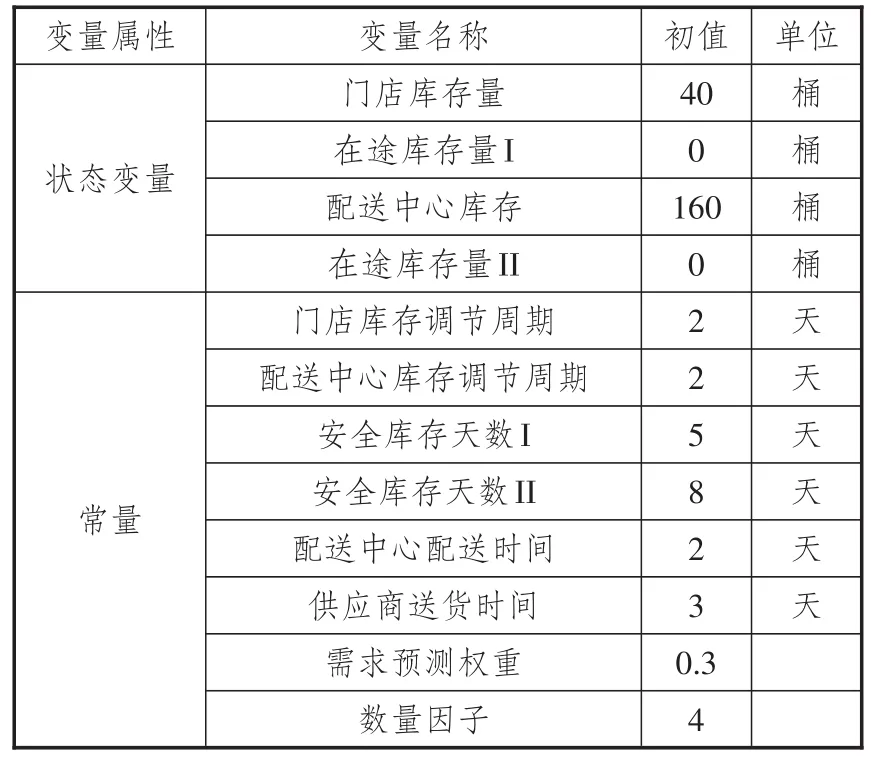
表3 设定模型变量初始值

在该初始值下的仿真结果如图3和图4所示。图3显示的是在模型初始条件下，门店库存量具有一定的波动性，平均库存量大约为28桶/天，相比于原始数据，库存量大幅下降，库存周转率为11.2天，也有了较大的提高。图4显示的是在初始情况下，订货次数和订货时间间隔较为平均，几次订货在数量上的差距也缩小了，与超市发原有的情况相比有较大优化。然而，这样的订货模式仍然存在小批次、大批量的问题。

（二）模型的优化与分析

对原模型进行敏感性分析，可以通过对常量的调整，看到它的变化对整个系统各个量的影响趋势，从而确定更为优化的取值。本文研究的多级库存各子系统具有一定相似性，故以下仿真实验仅以门店库存子系统和配送中心子系统为例分四种方案在不同参数下进行仿真实验，并对实验结果进行分析。模型整体敏感性实验如图5所示，相应实验结果如图6至图15所示，实验结果分析见表4：

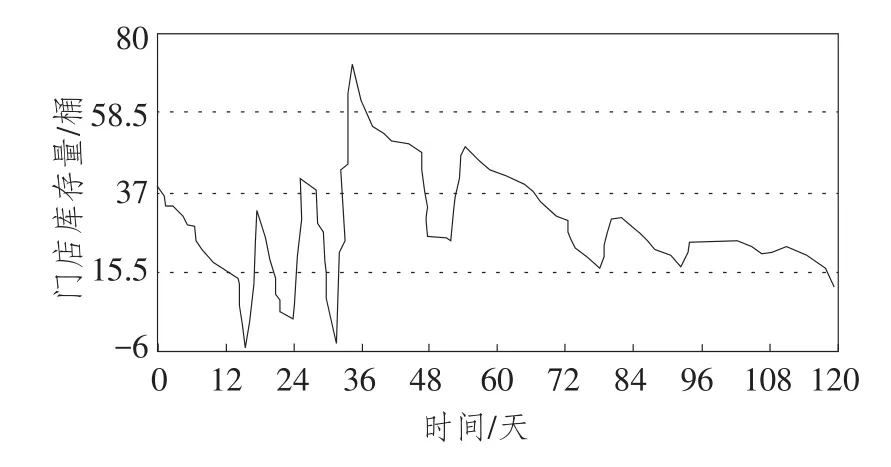
图3 门店库存量曲线

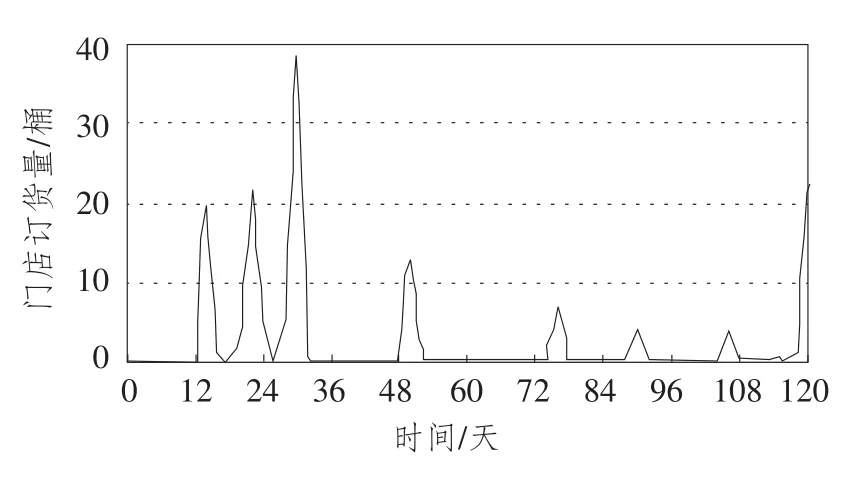
图4 门店订货曲线

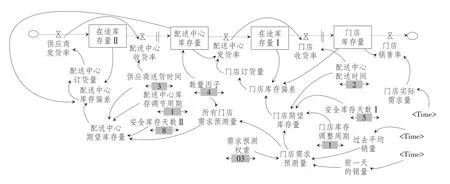
图5 模型的敏感性分析

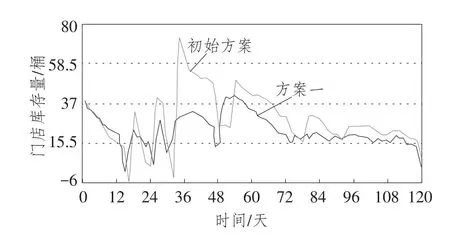
图6 初始方案与方案一门店库存量比较

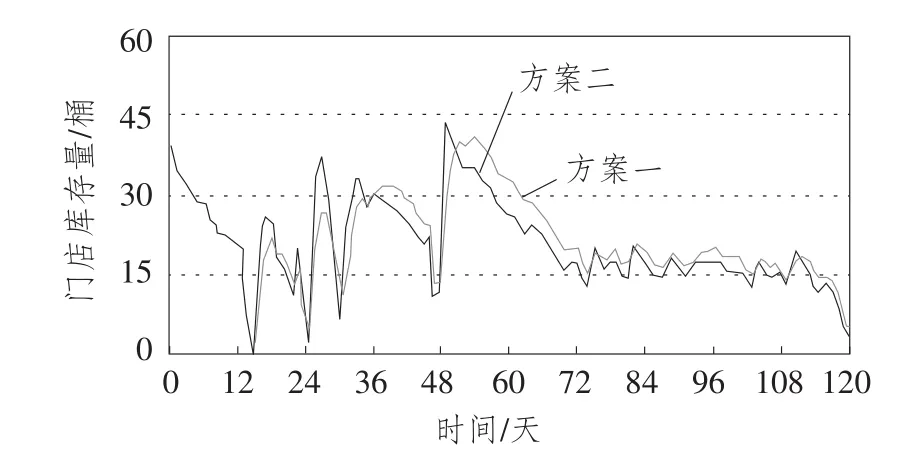
图7 方案二与方案一门店库存量比较

根据敏感性分析，本文对模型参数进行了反复修改，并根据每次修改的实验仿真结果，将时间步长（Time Step）、门店库存调节周期设为1，配送中心配送时间设为1，将需求预测权重设为0.4，安全库存天数设为6天。针对这一组经实验优化后的参数进行仿真，得到了一个较好的连锁零售多级库存动态优化模型，仿真结果如图16、图17、图18所示。

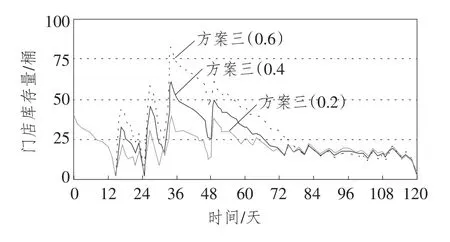
图8 方案三3种情况门店库存量比较

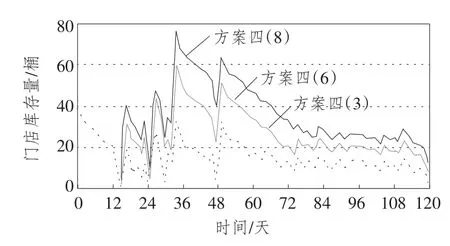
图9 方案四3种情况门店库存量比较

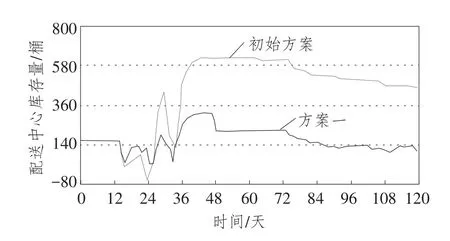
图10 初始方案与方案一配送中心库存量比较

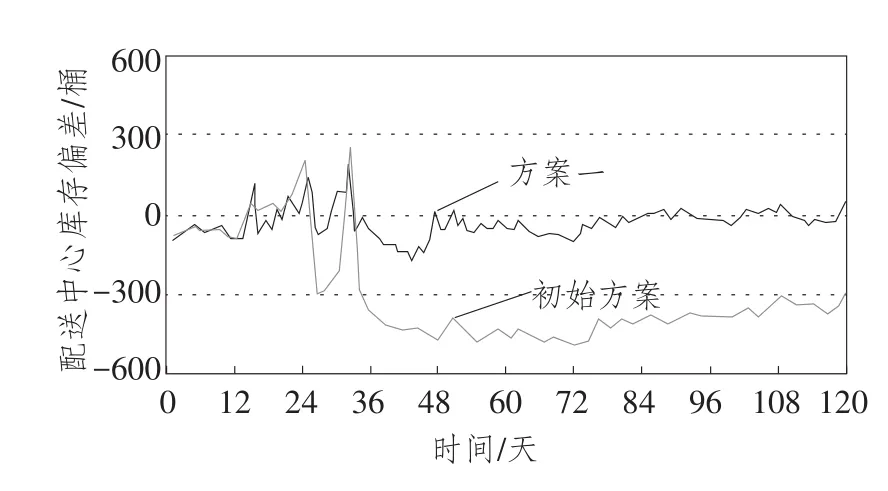
图11 初始方案与方案一配送中心库存偏差比较

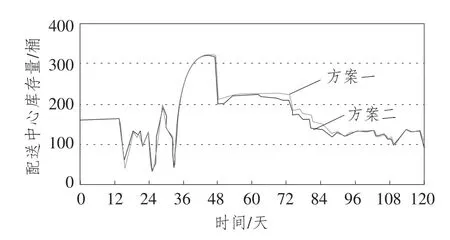
图12 方案二与方案一配送中心库存量比较

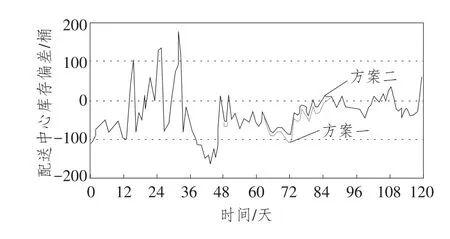
图13 方案二与方案一配送中心库存偏差比较

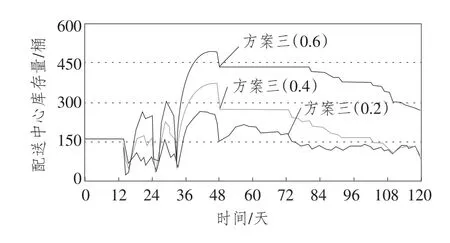
图14 方案三3种情况配送中心库存量比较

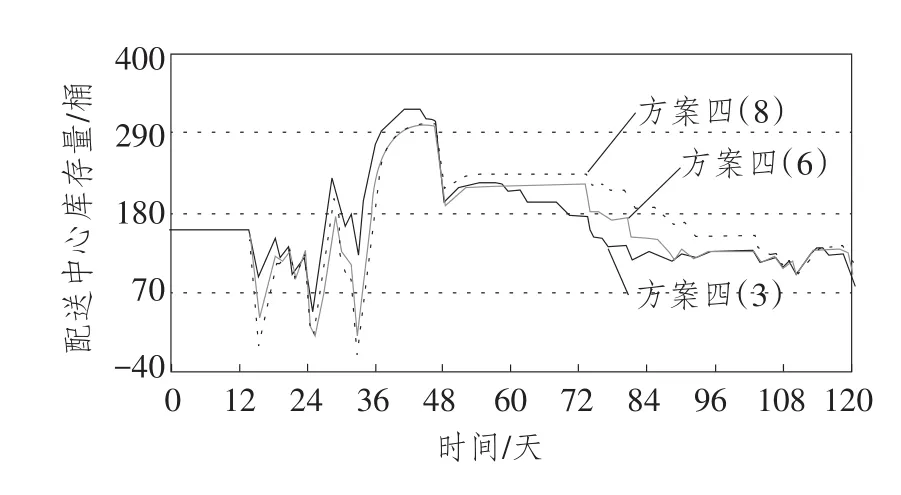
图15 方案四3种情况配送中心库存量比较

通过对仿真实验结果进行分析可以发现，改进后的多级库存系统与原有库存系统相比，无论是门店库存量还是配送中心库存量都大幅下降，多级库存各节点库存周转率也有所提高，在动态性、协同性、联动性、系统性等方面实现了多级库存系统的优化。综上所述，在连锁零售多级库存系统动力学的研究中，对于建立类似连锁零售商品的系统动力学模型可参考本系统设定需求预测权重、安全库存天数、门店库存调节周期等参数值。其他类型商品在进一步实验的基础上，也能取得较好的结果。

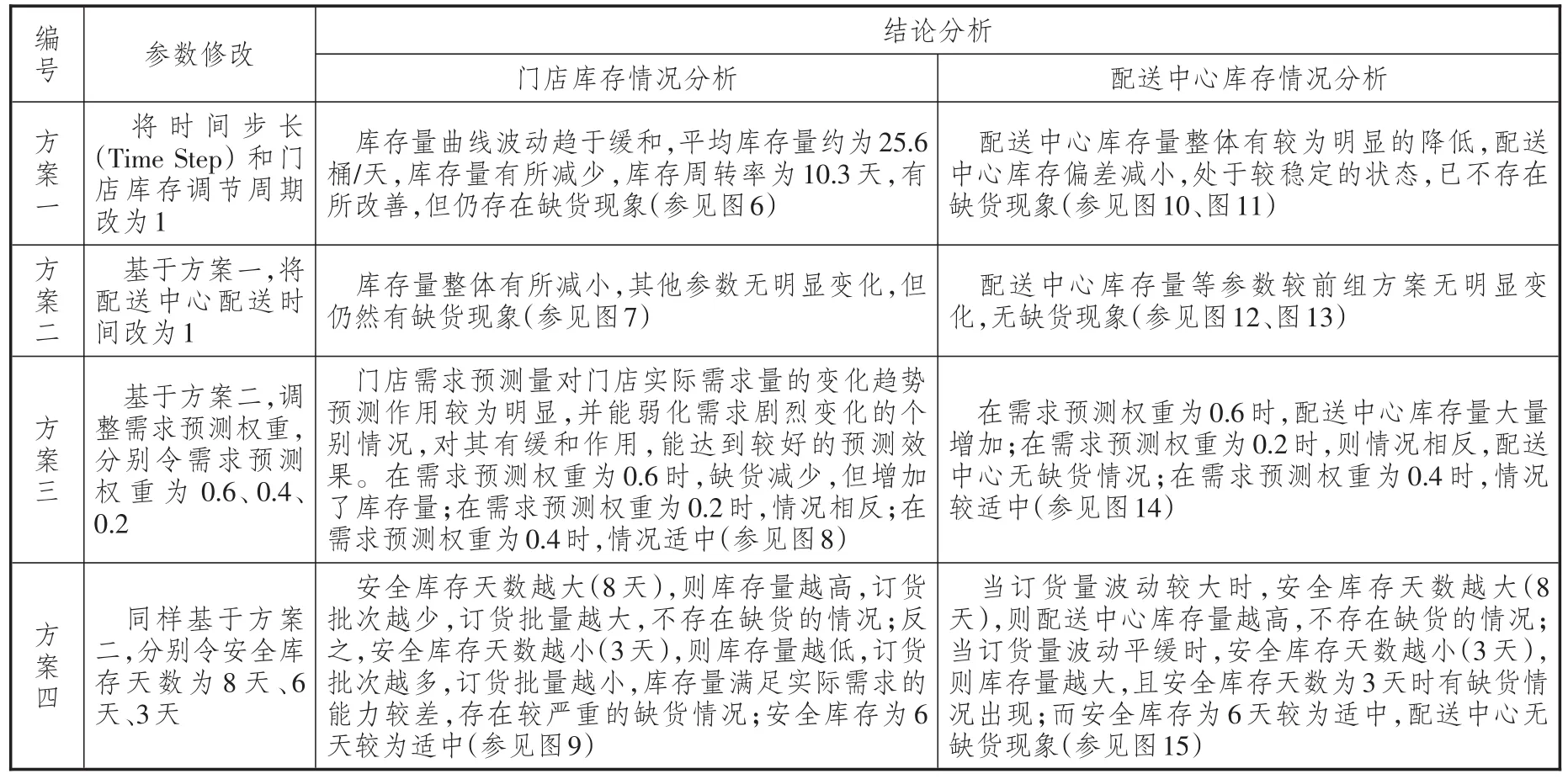
表4 敏感性实验结论分析

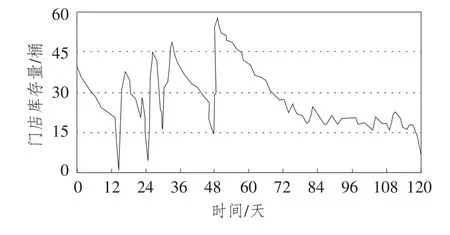
图16 改进后系统的门店库存量曲线

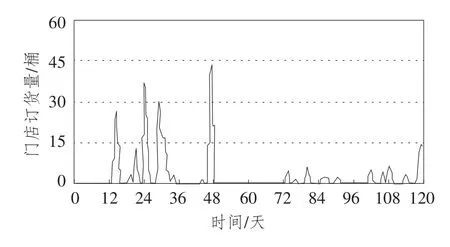
图17 改进后系统的门店订货量曲线

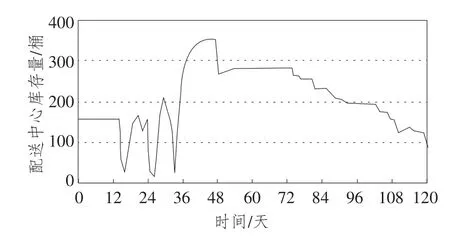
图18 改进后系统的配送中心库存量曲线

五、结论与展望

连锁零售多级库存管理是一项复杂的系统性工作，本文从实际应用和可操作性角度研究多级库存优化问题，建立了一个基于系统动力学的多级库存优化模型。通过敏感性分析和对需求预测权重、安全库存天数等参数的寻优，该模型有效兼顾了门店、配送中心等节点库存的优化，降低了整条供应链系统的库存量，减少了缺货情况，提高了库存周转效率，最终降低了库存成本。虽然得出的结论是基于对具体个案的仿真分析，但是由于所建立的系统动力学模型具有一般性的特点，仿真过程中又对个案给定的特征参数进行了大量的灵敏度测试，所以本文得出的结论对连锁零售多级库存具有一般性的指导和借鉴意义。

[1]柳键.基于时变需求的供应链基本库存水平优化研究[J].管理工程学报，2006（4）：146-148.

[2]郑霞忠，徐忠媛.中小型连锁超市物流系统优化研究[J].中国流通经济，2010（4）：30-33.

[3]赵川，薛红.MAS在连锁零售企业多级库存控制中的应用研究[J].运筹与管理，2013（1）：252-255.

[4]王其藩.高级系统动力学[M].北京：清华大学出版社，1995：79-86.

[5]赖新峰，陈志祥.营销策略对生产与库存决策影响的系统动力学仿真研究[J].中国管理科学，2012（20）：491-498.

[6]FORRESTER J W.Industrial dynamics：a major break⁃through for decision makers[J].Harvard business review，1958（4）：37-66.

[7]TOWILL D R.Dynamic analysis of an inventory and order based production control system[J].The international journal of production research，1982（6）：671-687.

[8]POLES R.System dynamics modelling of a production and inventory system for remanufacturing to evaluate system im⁃provement strategies[J].International journal of production economics，2013（1）：189-199.

[9]BALAJI J，JAMES R.Burns.Performance metric optimiza⁃tion advocates CPFR insupply chains：a system dynamics model basedstudy[J].Cogent business&management，2016（1）：1-20.

[10]张力菠，韩玉启，陈杰，等.供应链管理的系统动力学研究综述[J].系统工程，2005（6）：9-11.

[11]廖诺，张毕西，吴小结.不同需求条件下供应链系统动态仿真比较研究[J].运筹与管理，2010（4）：170-175.

[12]汪小京，刘志学，徐娟.基于系统动力学的第三方物流管理库存模型[J].系统管理学报，2016（2）：317-325.

[13]成琼文，周璐.基于系统动力学的绿色供应链管理实践路径仿真[J].科技管理研究，2016（23）：226-231.

责任编辑：方程

Abstract：In order to solve the problem of high inventory level，expensive inventory costs and low efficiency of inventory turnover in chain-retail industry due to inaccurate demand forecasting，inefficient reorder time and undynamic replenishment，we，from the view of system dynamics，proposed a multi-echelon inventory collaborative management model which consists of branch stores，distribution centers and suppliers.The raw data of inventory from a real chain retail company was collected to validate and simulate the proposed model on Vensim.Sensitivity analysis was carried out to optimize adjustment period，delivery time，demand forecast weight，safety inventory and other parameters.Results show that the proposed model can produce a lower inventory level，a more efficient inventory turnover rate and a lower inventory cost for multi-echelon inventory in retail chains.

Key words：system dynamics；chain retail；multi-echelon inventory optimization；Vensim

Research on Optimization and Simulation of Multi-echelon Inventory of Chain Retail based on System Dynamic

ZHAO Chuan and ZHANG Hao
（Beijing Technology and Business University，Beijing100048，China）

F713.1 文献标识码：A 文章编号：1007-8266（2017）10-0073-08

10.14089/j.cnki.cn11-3664/f.2017.10.009

赵川，张浩.基于系统动力学的连锁零售多级库存优化与仿真[J].中国流通经济，2017（10）：73-80.

2017-06-10

国家社会科学基金项目“我国生鲜农产品电子商务与传统流通体系的融合发展研究”（15BGL202）；北京市自然科学基金项目“深度不确定与大数据环境下连锁零售企业物流供应链预警决策研究”（9162002）；国家科技课题“农资物流安全配送关键技术与装备研究示范”（2015BAD18B01）

赵川（1988—），男，北京市人，北京工商大学商学院教师，博士，主要研究方向为库存控制与仿真，供应链管理；张浩（1978—），男，河北省唐山市人，北京工商大学商学院副教授，博士，主要研究方向为物流与供应链管理。