一种加权误差最小化的深度信念网络优化技术

吴 强，杨小兵

(中国计量大学 信息工程学院,浙江 杭州 310018)

一种加权误差最小化的深度信念网络优化技术

吴 强，杨小兵

(中国计量大学 信息工程学院,浙江 杭州 310018)

传统的深度信念网络模型缺乏并行有效的算法来确定网络层数以及隐藏层神经元的数目，实验时大多依据经验来选取，这样做不仅使得模型训练困难，且范化能力差，影响实验结果.针对此问题，通过比较重构误差和验证集错误分类率的乘积(加权误差)大小来选取网络层数，网络层数确定后，再根据重构误差使用渐增法或二分法来选择合适的隐层神经元数目，以使整个模型达到最优.实验结果表明，用上述方法确定模型网络层数及隐藏层神经元数目，能有效提高模型分类或预测的精度.

深度信念网络；网络层数；神经元数目；重构误差；加权误差

Abstract: The traditional deep belief network model lacks parallel and effective algorithm to determine the number of network layers and the number of hidden neurons. Most of the experiments chose them by experience. This makes the model training difficult. This paper chose the number of network layers according to the size of the reconstruction error and the product of the error classification rate of the verification set (weighted errors). After the network layers were determined, the number of hidden neurons was selected according to the reconstruction error by the incremental method or dichotomy method. The experimental results show that the number of model network layers and the number of hidden neurons with the method can improve the accuracy of model classification or prediction.

Keywords: deep belief network; network layers; number of neurons; reconstruction error; weighted error

人脑对事物的认知过程是逐层进行、逐步抽象的，大脑通过提取从外界接收到的信号，每次处理接收到信号中一个或多个的特征，最终将一个抽象的概念传递给人脑，形成了人对某种事物的认知.人工神经网络[1]通过模拟大脑的工作方式，在很多方面的表现甚至超过人脑，因此受到学者们的广泛关注.人工神经网络曾一度因为中间层网络权值调整困难而陷入低谷，后来在BP算法[2]出现后又再次活跃起来.在20世纪九十年代，又随着支持向量机[3]提出而再次陷入低谷.直到2006年，深层次神经网络的训练算法有了重大突破，并把神经网络的发展引入到一个完全新的领域——深度学习[4]，使得人工神经网络再次成为人们关注的焦点.深度学习作为人工智能和机器学习的一个新的领域，由于其优秀的特征学习能力而成为移动互联网和大数据的热潮，并取得了突破性进展.2012年11月，微软在中国天津的一次活动上展示了一个全自动同声翻译系统，演讲者用英文演讲，后台计算机自动地完成英文语音识别、英中翻译以及中文语音合成过程，效果十分流畅，而这台机器所使用的的关键技术正是深度学习.这大大鼓舞了深度学习的发展，目前深度学习已经成为人工智能未来发展的主要方向.

深度信念网络[5](Deep Belief Network, DBN)作为深度学习的重要模型，足够的隐藏层数保证网络能够学习到数据的本质特征，其逐层无监督训练算法克服了多隐层神经网络训练困难的问题，实现了多隐层神经网络建立工作的突破，目前已成为深度学习的研究热点.尽管深度信念网络已经成功应用于多个领域，如人脸表情识别[6]，自然语言处理[7]，时间序列预测[8]等，但仍存在着许多问题尚待解决.目前深度信念网络的网络层数及神经元数目缺乏科学有效的选取方法，大多依靠经验来人工选取，不能充分发挥深度信念网络的优势，有时实验结果甚至不如浅层网络.

本文以重构误差和验证集分类错误率的乘积(加权误差)大小作为选取网络隐藏层数的标准，再根据重构误差来调整隐藏层神经元数目，可以使网络层数及神经元数目处于较优的水平，能有效提高训练效率，使实验结果更准确.

1 深度信念网络

深度信念网络是一种包含多个隐层的神经网络模型，它通过训练数据来学习数据的有效特征，尤其在分类或预测方面，其优势更加明显.

受限玻尔兹曼机[9](Resteicted Boltzmann Machine, RBM)是DBN的基本组成元素，它是一种具有两层结构的二部图，包含可见层v和隐藏层h，同一层内神经元间无连接，不同层神经元间全连接，其结构如图1.

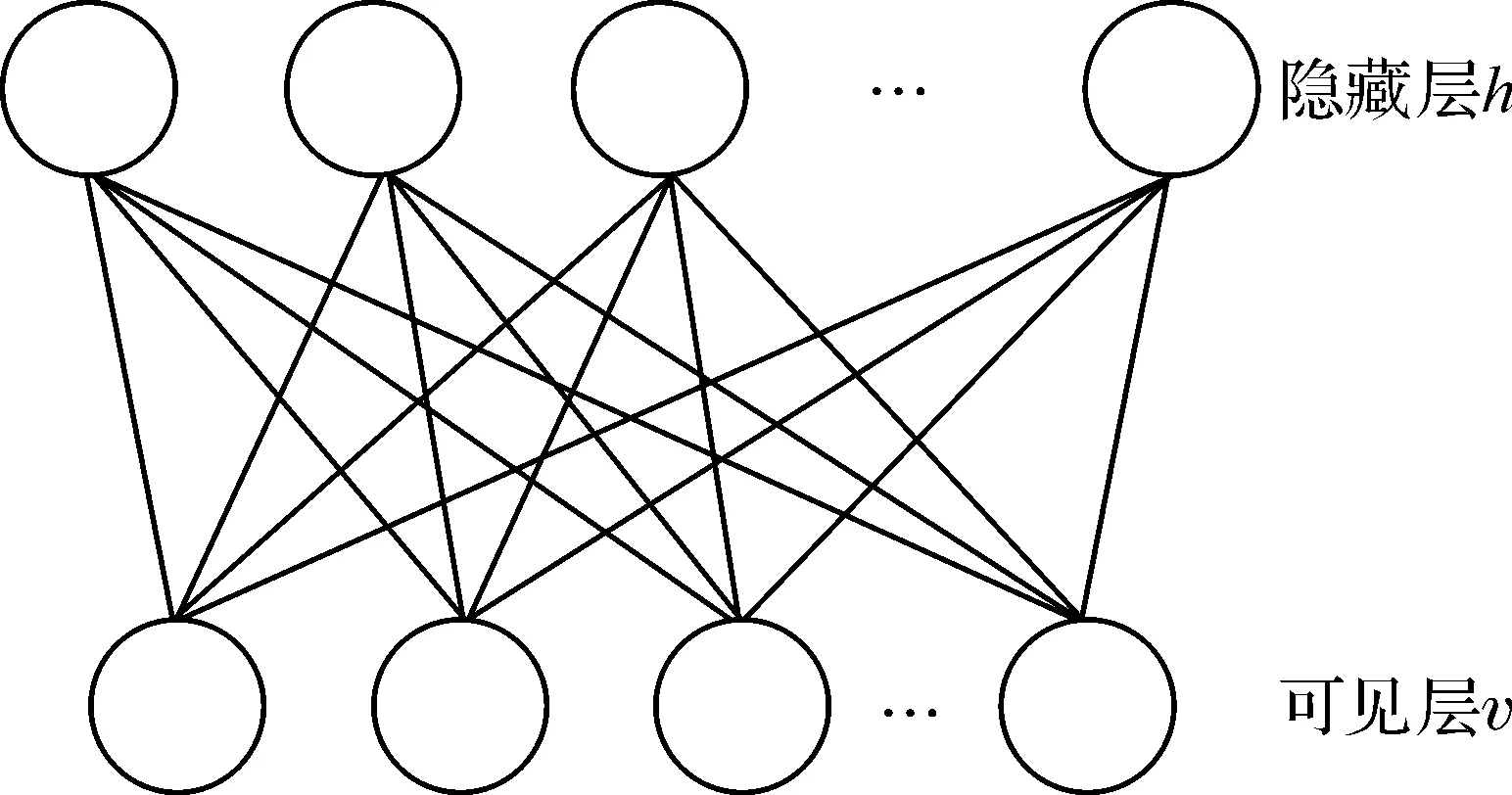
图1 受限玻尔兹曼机模型Figure 1 Resteicted Boltzmann Machine model

深度信念网络通常是由多个RBM依次叠加而形成，其结构如图2.

图2 深度信念网络模型Figure 2 Deep belief network model

DBN是一种基于能量的模型，其能量函数为

E(v,h|θ)=

(1)

其中vi、ai分别表示可见层节点及偏置，hj、bj分别表示隐藏层层节点及偏置，wij表示可见节点vi与隐藏节点hj间的连接权值.对于每个RBM，当我们给定可见层节点的值时，我们可以得到隐藏层节点的分布，即

(2)

同样，我们在知道隐藏层节点值时，也可以求出可见层节点的分布，即

(3)

其中sigm( )为Sigmoid函数.

DBN模型的训练算法为逐层无监督贪心算法，训练数据均为无标签数据.训练时，先用CD[10](Contrastive Divergence, CD)算法训练第一层RBM，得到第一层RBM的参数后，固定此参数，并将第一层RBM的输出作为下一个RBM的输入，继续训练下一层的RBM.如此反复，直到整个网络训练完成.由于模型使用逐层无监督算法来训练，模型获取了数据的潜在特征，使得模型参数已经处于一个较优的水平，避免了网络因随机初始化参数而训练困难和易陷入局部最小值的问题.最后，再使用有标签的数据来反向微调模型的参数，使整个模型达到最优.

2 深度信念网络优化技术

关于多隐层人工神经网络，我们可以知道[11]：

1)含有多个隐藏层的人工神经网络具有优秀的特征学习的能力，能更加准确地刻画学习数据的本质特征，提升分类或预测的准确性；

2)深层次的神经网络训练困难的问题可以通过逐层无监督训练算法解决.

这说明随着网络层数的增加，网络模型提取到的特征质量就越高，从而提升实验结果的准确性.但当网络层数超过某一个阈值后，模型的参数个数会超过训练样本个数，从而模型获取的是当前训练数据的特征而非数据的整体特征，从而出现过拟合(Over-fitting)现象，使得实验结果产生较大误差.因此，选取合适的网络层数和神经元数目非常重要.

深度信念网络有着优秀的特征学习能力，而重构误差(Reconstruction Error, RE)可以用来衡量模型提取到特征的好坏，重构误差是数据经过RBM的分布进行Gibbs转移[12]以后得到的结果与实际值之间的差异，即

(4)

WE=RE×ε.

(5)

其中ε是验证集错误分类率(error classification rate of the verification set,ε)，即DBN预训练完成后，将模型用于验证集分类，模型分类错误的个数所占比率.

当模型的隐藏层数以及神经元的数目较优时，模型能更好的拟合数据，相应的验证集错误分类率也会很小.通过比较加权误差的大小来选取网络隐藏层数，这个值越小，说明重构误差和错误分类率也越小，模型就越优秀.

网络模型隐藏层数确定以后，我们需要再确定每个隐层神经元的数目.前面我们提到，重构误差是衡量模型提取数据特征的标准，当神经元数目较优时，模型同样也会提取到优秀的特征，从而重构误差的值也较小.因此，我们可以根据重构误差来确定神经元的数目.我们先设定所有隐层神经元数目的初值，然后逐渐地增加或减少，比较不同数目神经元下重构误差的大小，然后选出最优神经元数目.在此，本文给出两种选取神经元数目方法，如算法1，算法2.

算法1：渐增法

1)设定所有隐层神经元数目的的初始值，并计算当前重构误差.

2)所有隐层神经元数目同时增加K个，比较重构误差大小，确定最优神经元数目所在区间.

3)重复步骤2)(K值可变)，直到确定的区间之间的距离小于给定阈值时执行下一步.

4)在步骤3)得到的区间中，每层神经元依次增加L个，考虑所有可能的排列组合，选择重构误差最小的组合作为隐藏层神经元数目.

5)结束.

算法2：二分法

1)通过实验确定隐藏层神经元数目的上限，并设为初始值，计算出重构误差.

2)将各层神经元数目变为原来的一半，比较重构误差大小，确定最优神经元数目所在区间.

3)重复步骤2)，直到选取区间的距离小于给定阈值时，执行下一步.

4)在步骤3)得到的区间中，将每层神经元数目依次增加L个，考虑所有的排列组合，选择重构误差最小的组合作为隐藏层神经元数目.

5)结束.

整个实验流程如图3.

图3 实验流程图Figure 3 Experimental process

至此，我们完成了网络层数及隐层神经元数目的选取.

3 实验结果分析

3.1MNIST手写字体分类实验

MNIST数据库是一个关于手写数字识别的数据库，将手写数字0～9归一化并集中在一个固定大小的图像上.本文选取其中的7 000张图片，其中5 000张作为训练集，1 000张作为验证集，1 000张作为测试集.首先我们需要确定网络的深度，通过不同隐藏层数的重构误差以及验证集错误分类率计算出WE，结果如表1.

表1 不同隐层数WE变化表

通过表1我们可以知道，在网络层数超过2层以后，重构误差虽然整体上有下降趋势，但波动较大，再通过比较验证集错误率我们发现，网络隐藏层数超过2层以后，其分类错误率不断上升，而此时WE也最小，因此，网络合适的隐藏层数目为2层.

接下来需要再确定隐层神经元的数目，先初始化神经元数目为[50,50]，然后每次增加50，比较它们重构误差以及分类错误率的大小，其重构误差变化如图4.

图4 MNIST数据RE变化图Figure 4 RE changes in MNIST data

观察图4，随着神经元数目的不断增加，第一层RBM的重构误差在缓慢减小后基本保持不变，第二层RBM的重构误差随着神经元数目的增加不断震荡，在神经元数目从300增加到350的过程中不断减小并达到最小值，因此最优神经元数目大致在300到350之间.我们将第一个隐藏层神经元数目从300开始，每次增加10个，第二隐藏层同样从300开始每次增加10个，即神经元数目的所有可能情况为[310,310]，[310,320]，[310,330]，...，[350,350]，共有25种，其重构误差图像如图5.

通过图5我们可以看到，在编号为17的组合即隐藏层神经元数目为[340,320]时，重构误差达到最小，故各层最优神经元数目依次为340、320.至此，模型构建完成.我们用此模型对测试集进行测试，其正确分类概率达到了96.76%.

图5 MNIST数据不同神经元RE变化图Figure 5 RE changes of different neurons in MNIST data

3.2 MAGIC伽马成像数据集分类实验

大气切伦科夫望远镜伽马成像数据集(MAGIC Gamma Telescope Data Set)是UCI中一个非常优秀的数据分类集，用来模拟大气切伦科夫望远镜中高能γ粒子的定位，这个数据集共有19 020个数据.部分数据集如表2

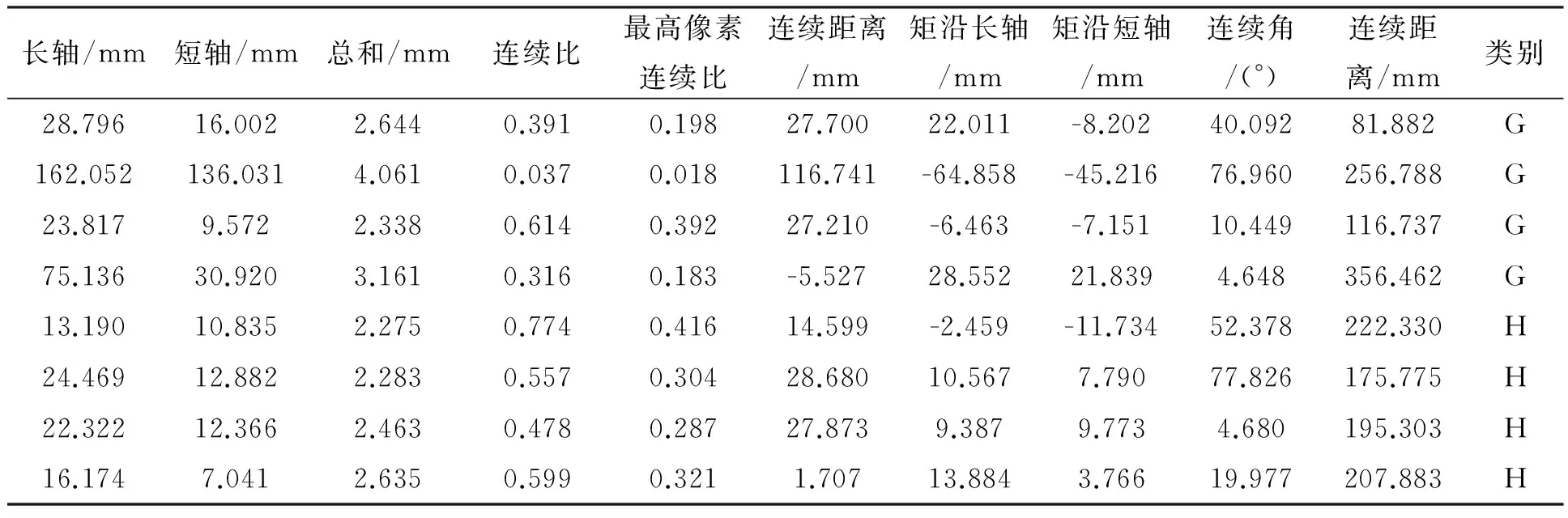
表2 部分MAGIC 伽马成像数据集

它共有10个预测属性，用来预测两类结果：G类(0)和H(1).本文选取其中10 000条数据，G类和H类各5 000条，其中8 000条作为训练集，1 000条作为测试集，剩下1 000条作为验证集.实验开始前先对数据进行归一化处理，归一化完成以后，用DBN模型对数据进行训练，得到不同隐藏层数时，网络的重构误差、验证集错误分类率以及WE如图6～8.

观察上面3副图像，当网络隐藏层超过2层以后，其重构误差大大增加，虽然在隐藏层数为5和6时有所下降，但验证集错误分类率随着隐藏层数的增加而不断变大，且在隐藏层数为5时达到最大；再观察WE的图像，我们发现当网络隐藏层数为2时WE值最小，故合适的网络隐藏层数为2层.

图6 MAGIC数据不同隐层RE变化图Figure 6 RE changes of different neurons in MAGIC data

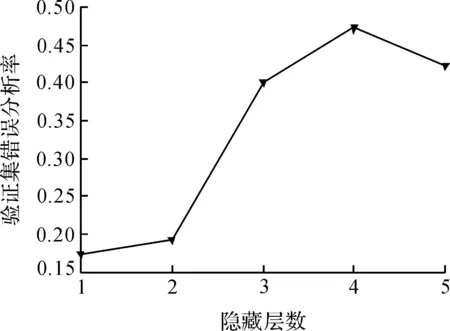
图7 MAGIC数据不同隐层错误分类率Figure 7 ε changes of different hidden layers in MAGIC data

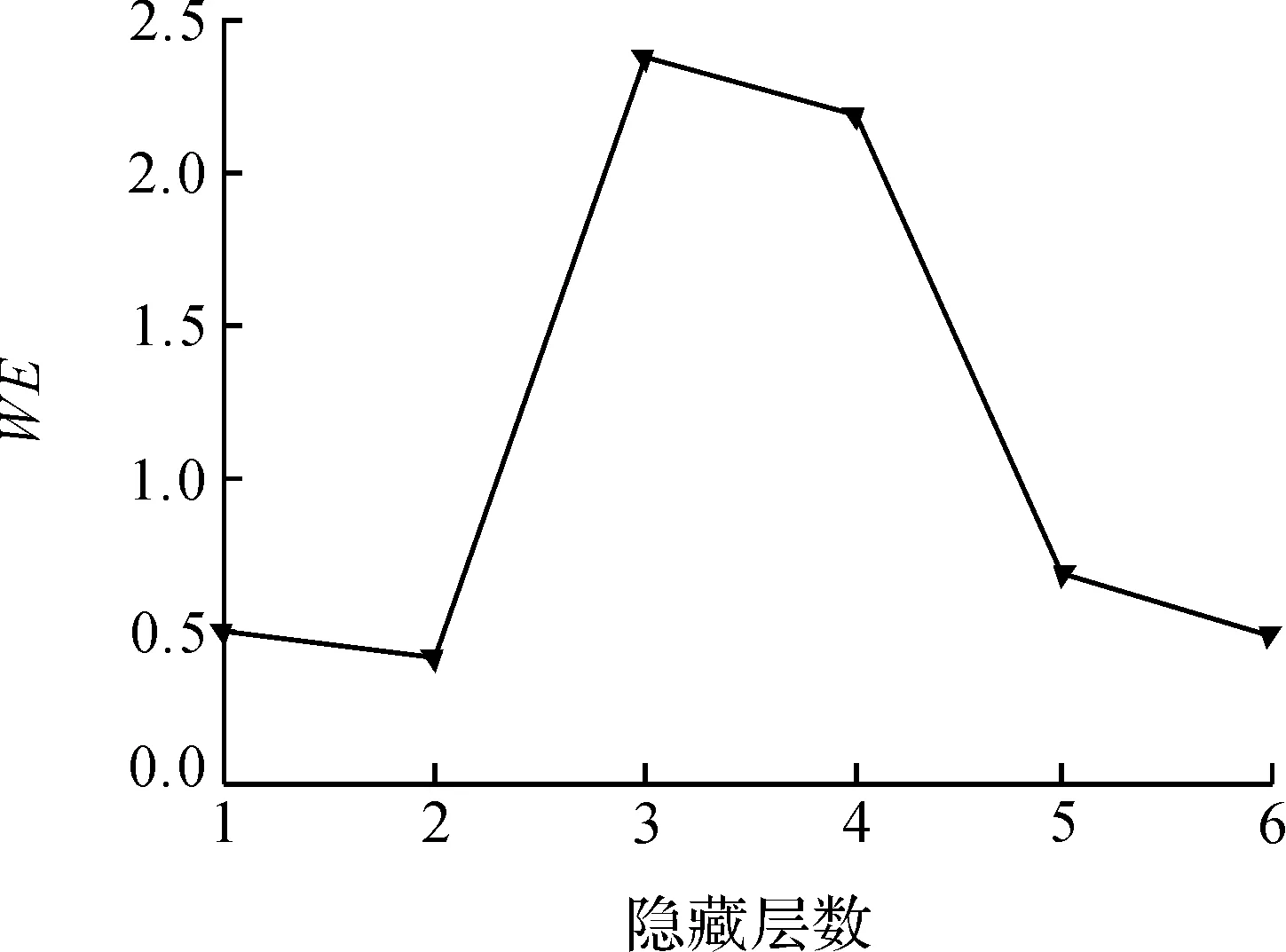
图8 MAGIC数据不同隐层WE变化图Figure 8 WE changes of different neurons in MAGIC data

模型的输入层为10个神经元，输出层为2个神经元，我们还需要确定中间两个隐藏层的神经元数目.当隐藏层神经元数目最优时，模型提取数据的特征就越优秀，其重构误差也会比较小，故我们根据重构误差来确定隐层神经元数目.通过实验，我们发现当两个隐藏层神经元数目达到400以后，再增加神经元数目，其重构误差大大增加，而验证集错误分类率也迅速变大，这说明最优神经元数目应该小于400.接下来我们用二分法来寻找最优神经元数目，将初始隐藏层神经元数目设为[400 400]，然后依次递减一半，得到重构误差如图9.

观察图9，当隐层神经元数目从200递减到100的过程中，其重构误差大大减小，而从100递减到50的过程中又增加，所以最优神经元数目应该在100～200之间，我们继续用二分法寻找最优神经元个数，通过比较重构误差，其最优神经元个数区间为175～200.

为了寻找更精确的隐藏层数目，将两个隐藏层分开考虑，我们将第一和第二个隐藏层神经元数目从175开始依次增加5个，考虑所有排列组合，共有36情况，不同情况下重构误差如图10.

图9 MAGIC数据集二分法RE变化图Figure 9 RE changes with dichotomy in MAGIC data set

图10 MAGIC数据不同神经元数目REFigure 10 RE changes in different neurons of MAGIC data

通过图10我们发现序号为12的组合重构误差最小，即神经元数目为[185,180].故最终模型结构为10-185-180-2，我们将模型用于集测试，其分类正确率达到96.25%.至此，我们完成了网络模型构建，且网络深度和神经元数目相对较优.

4 结 语

本文详细介绍了深度信念网络的模型结构以及其训练过程，针对网络隐藏层数及神经元数目难以选择的问题，提出根据重构误差和验证集错误分类率的乘积大小来选取合适的隐层数，并根据重构误差来调整神经元数目.这样就能有效避免因依据经验选取隐藏层数和神经元个数不当而引起的训练困难问题，降低运算成本，提高预测或分类的准确率.

[1] NEOCLEOUS C, SCHIZAS C. Artificial neural network learning: a comparative review[C]//MethodsandApplicationsofArtificialIntelligence,SecondHellenicConferenceonAI,SETN2002. Berlin: Springer, 2002:300-313.

[2] 温林强, 夏凤毅, 沈洲. BP神经网络多波长法的COD预测[J]. 中国计量学院学报, 2016, 27(3):306-312. WEN L Q, XIA F Y, SHEN Z. COD prediction based on BP neural networks with multi-wavelength methon[J].JournalofChinaUniversityMetrology, 2006, 27(3):306-312.

[3] ADANKON M M, CHERIET M. Optimizing resources in model selection for support vector machine[J].PatternRecognition, 2007, 40(3):953-963.

[4] 尹宝才, 王文通, 王立春. 深度学习研究综述[J]. 北京工业大学学报, 2015(1):48-59. YIN B C, WANG W T, WANG L T. Review of deep learning[J].JournalofBeijingUniversityofTechnology, 2015(1):48-59.

[5] KUREMOTO T, KIMURA S, KOBAYASHI K, et al. Time series forecasting using a deep belief network with restricted boltzmann machines[J].Neurocomputing, 2014, 137(15):47-56.

[6] LIU P, HAN S, MENG Z, et al. Facial expression recognition via a boosted deep belief network[C]//IEEEConferenceonComputerVisionandPatternRecognition. Columbus: IEEE Computer Society, 2014:1805-1812.

[7] LEFEVRE F. A DBN-based multi-level stochastic spoken language understanding system[C]//SpokenLanguageTechnologyWorkshop. Aruba: IEEE, 2006:78-81.

[8] KUREMOTO T, KIMURA S, KOBAYASHI K, et al. Time series forecasting using a deep belief network with restricted boltzmann machines[J].Neurocomputing, 2014, 137(15):47-56.

[9] TOMCZAK J M, ZIEBA M. Classification restricted boltzmann machine for comprehensible credit scoring model[J].ExpertSystemswithApplications, 2015, 42(4):1789-1796.

[10] HINTON G E. Training products of experts by minimizing contrastive divergence[J].NeuralComputation, 2002, 14(8):1771-1800.

[11] HINTON G E, SALAKHUTDINOV R R. Reducing the dimensionality of data with neural networks.[J].Science, 2006, 313(30):504-507.

[12] DAS S, PEDRONI B U, MEROLLA P, et al. Gibbs sampling with low-power spiking digital neurons[C]//IEEEInternationalSymposiumonCircuitsandSystems. Portugal: IEEE, 2015:2704-2707.

[13] 潘广源, 柴伟, 乔俊飞. DBN网络的深度确定方法[J]. 控制与决策, 2015(2):256-260. PAN G Y, CHAI W, QIAO J F. Calculation for depth of deep belief network[J].ControlandDecision, 2015(2):256-260.

Adeepbeliefnetworkoptimizationtechniquebasedonweightederrorminimization

WU Qiang，YANG Xiaobing

(College of Information Engineering, China Jiliang University, Hangzhou 310018, China)

2096-2835(2017)03-0352-07

10.3969/j.issn.2096-2835.2017.03.014

2017-04-29 《中国计量大学学报》网址zgjl.cbpt.cnki.net

TP391

A