射线束分析仪的单轴位移精确度校准研究

李云鹏，郭天太，赵 军，孔 明

(中国计量大学 计量测试工程学院，浙江 杭州 310018)

射线束分析仪的单轴位移精确度校准研究

李云鹏，郭天太，赵 军，孔 明

(中国计量大学 计量测试工程学院，浙江 杭州 310018)

射线束分析仪在大型放疗设备的校准中有重要作用，其自身定位精确度在0.1 mm.通过搭建基于激光跟踪仪的位移测试系统，对射线束分析仪水平轴的定位精度进行测量校准.将测得的位移数据进行最小二乘拟合，使得拟合曲线上的各点位移与真实位移值之差的平方和最小，此时拟合曲线上各点位移值最接近真实位移.将拟合曲线上各点位移值与标准位移值做差，即可求得各点误差值.实验结果表明，在未使用小支架的情况下位移测量系统的基本误差为0.163 6%，利用小支架使激光跟踪仪光束不穿过水箱壁时，位移测量系统的基本误差为0.061 6%.实验系统可使射线束分析仪的单轴位移精确度达到0.01 mm精度级.

射线束分析仪；激光跟踪仪；小支架；位移精确度

Abstract: The position accuracy of beam analyzers is 0.1 mm. In this paper, the position precision of the beam analyzer’s X axis was calibrated through the construction of a displacement test system. The measured data was fit with the least squares to assure that the sum of squres of the difference between the values on the fitting curves and the actual displacement was the least. The value on the fitting curve was closest to the real displacement value. The experimental results showed that the basic error of the measurement system was 0.163 6%. under the condition of no small brackets. When small bracket was used, the laser tracker beam could not go through the tank wall, and the basic error of the measurement system decreased to 0.061 6%. The single-axis displacement precision of the beam analyzer reached 0.01mm in the experimental system.

Keywords: ray beam analyzer; laser tracker; small bracket; displacement accuracy

随着当代医疗水平的不断调高，射线束分析仪作为放疗领域的重要校准设备，其测量精确度也亟待进一步提高.目前，国际上走在前列的相关国家，如德国、日本、瑞典、美国、英国等都已初步建立起或正在建立医用加速器水吸收计量基准[1].加速高能光子及射线束研究是国际计量研究的前沿领域，国际计量局于2009年开始组织相关国家机构进行比对.截止到目前，美国、德国、加拿大已完成相关比对工作，我国也于2010年正式启动射线束水吸收剂量的相关比对工作，并于2015年取得阶段性成果.

目前针对于射线束分析仪的校准，主要从放射场强度检测方面进行，在其定位精度方面鲜有研究.针对这一问题，本文着眼于射线束分析仪单轴位移精确度，进行了射线束分析仪水平轴位移精确度校准与数据分析两方面的研究.

1 激光跟踪仪的工作原理

激光跟踪仪的原理如图1，它本质上是由激光干涉测距和自动跟踪测角测距两个模块所组成的全站仪，跟踪头的激光束、旋转镜和旋转轴构成了激光跟踪仪的三个轴，三轴相交的中心是测量坐标系的原点[2]

图1 激光跟踪仪原理图Figure 1 Principle diagram of the laser tracker

本实验所用为AT901-LR型激光跟踪仪，它的横向跟踪速度≥4 m/s，径向跟踪速度≥6 m/s，一次测量直径为160 m，其测距精确度为全量程(半径80 m)内不超过10 μm，位移测量精确度随测量距离的减小而增大.它可静态或动态地跟踪一个在空中运动的物体，由此形成球坐标测量系统，并测得三位置参量α、β、γ即可确定目标物在直角坐标系的位置矢量OP=(x,y,z)，

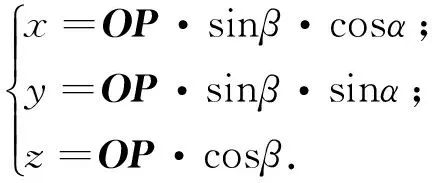
(1)

其中，是由两个角度编码器读出的，由干涉测距模块测得的信号，经整形、放大后输入可逆计数器计算出脉冲总数，得到OP的距离值，最终由电子计算机按式(1)计算出目标物的位置矢量OP即动态坐标值(x,y,z).

2 测量系统的组成及测量方法

2.1 测量系统的组成

测量系统组成如图2所示，将激光跟踪仪固定在移动基座上，距三维水箱0.5 m处，以保证各测量模式的稳定性[3].

图2 测量系统组成图Figure 2 Measuring system constitutional diagram

激光跟踪仪的测量主要由靶球反射的激光束进行空间定位，因此，靶球应固定于射线束分析仪的电离室载台上.三维水箱的水平轴为悬臂结构，所以电离室载台不能运动至水平轴的末端.

在水箱无水的情况下，将激光跟踪仪的靶球粘合在待测轴的电离室载台上，如图3(a)，通过计算机控制系统移动载台在轴上的位置，通过激光跟踪仪测得此时电离室载台的准确位移量.

当系统在正常使用条件下(充满水)对待测轴的定位准确性进行检测时，激光跟踪仪的反射球不能没入水中[4]；同时，由于激光跟踪仪的高度与三维水箱的高度接近，导致测量高度略低于水箱，光束需要透过水箱有机玻璃壁(20 mm)进行测量，也会导致测量数据产生误差.综合以上两个问题，实验中设计了一个小支架(300 mm)，下端固定于电离室载台上，上端可使反射球高于水面，此时光束不用透过水箱壁，如图3(b)，再次进行测量.

2.2 单轴位移数据测量方法

在水平轴的测量范围内分别设置探测器运动至包含最小位置到最大位置在内的多个位置点,水平轴上取7个测量点.电离室载台每次从起始点运动到设置值的实际位置处，得到两者间位移之差.运动至最大位移点后按逆向顺序重新测量至起始点.激光跟踪仪复位，进行下一次测量.测量轨迹为(50,0,0) →(100,0,0)→(150,0,0)→(200,0,0)→(250,0,0)→(300,0,0)→(350,0,0)→(300,0,0)→(250,0,0)→(200,0,0)→(150,0,0)→(100,0,0)→(50,0,0)，进行3次循环测量.

图3 待测轴结构Figure 3 Shaft structure under test

3 单轴位移数据的处理与校准

3.1 测量数据的处理

利用激光跟踪仪所测得的数据为三维矢量，对水平轴位移校准只需知道其X轴的坐标值，因此需要对其Y轴和Z轴的位移数据加以剔除.激光跟踪仪测量结果如表1.当引入小支架时其测量结果如表2.

由激光跟踪仪测得的各点的真实值与射线束分析仪给出的理论值可知各点的误差为

ΔA=Ad-As.

(2)

其中Ad为测量值，As为射线束分析仪位移控制系统所设置的标准值.由式(2)中各点的误差

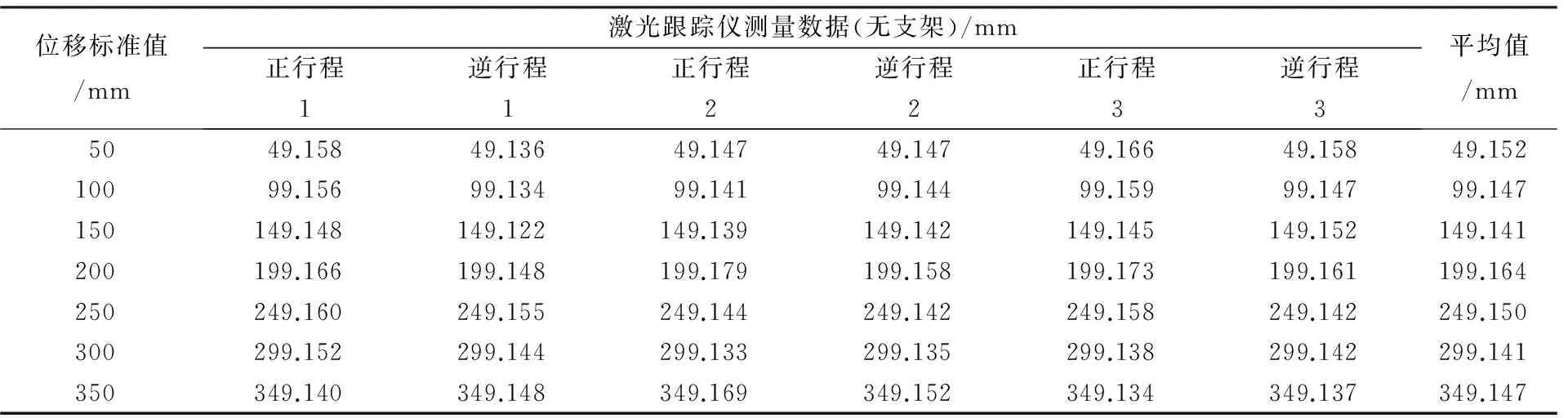
表1激光跟踪仪测量数据(无支架)

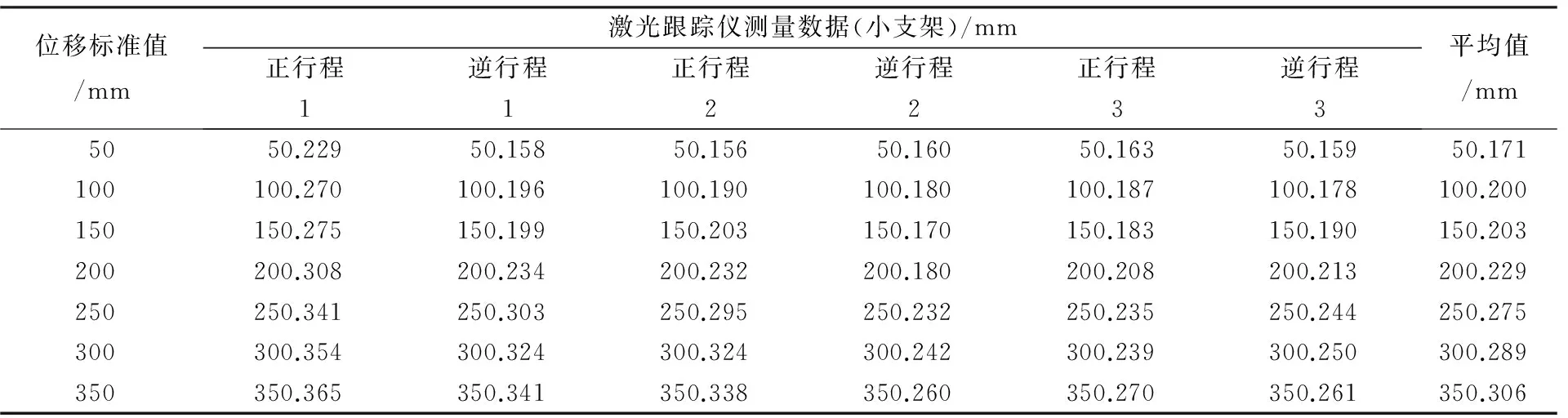
表2 激光跟踪仪测量数据(小支架)

值可得位移测量系统的基本误差为

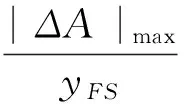
(3)

其中|ΔA|max为绝对误差中ΔA绝对值最大者；yFS为射线束分析仪水平轴上可测的最大量程.

3.2 最小二乘法数据拟合

最小二乘直线回归算法作为线性测量的经典拟合算法得到了广大科技人员的认可，在提高位移测试系统的可靠性的同时又能保持较高的系统测试精度.在一些精度要求较高的实验场合，用激光跟踪仪测量，并利用计算机强大的数据处理能力对校准数据进行高次方程拟合可达到较高的测量准确度.

对于一系列所给出的特定的数据点集{(xi,yi)}(i=0,1……n)，在选定的函数类P中，求f(x)∈P，使得各数据点误差的平方和∑[f(xxi)-yi]2为最小[5]，则函数f(x)称为该数据点集的最小二乘解或拟合函数.对于前面所给定的已知数据点集(xi,yi)(i=0,1,……n)，所得到的拟合曲线函数f(x)，可使各点差值的平方和∑[f(xxi)-yi]2最小[6].

图4为在未使用小支架的情况下，激光跟踪仪的光束透过水箱壁与水时，测量得到的结果.由图可知，当未使用小支架进行测量时[7]，待测轴位移的最大误差的平均值为-0.87 mm，所有测量点的误差平均值为-0.851 mm.由此可见，激光束的折射对测量影响较大.此时，各点集的最小拟合函数为

f(x)=-0.001 2x-0.725 6.无小支架的情况下，位移测量系统的基本误差[8]为

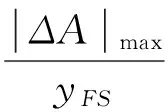
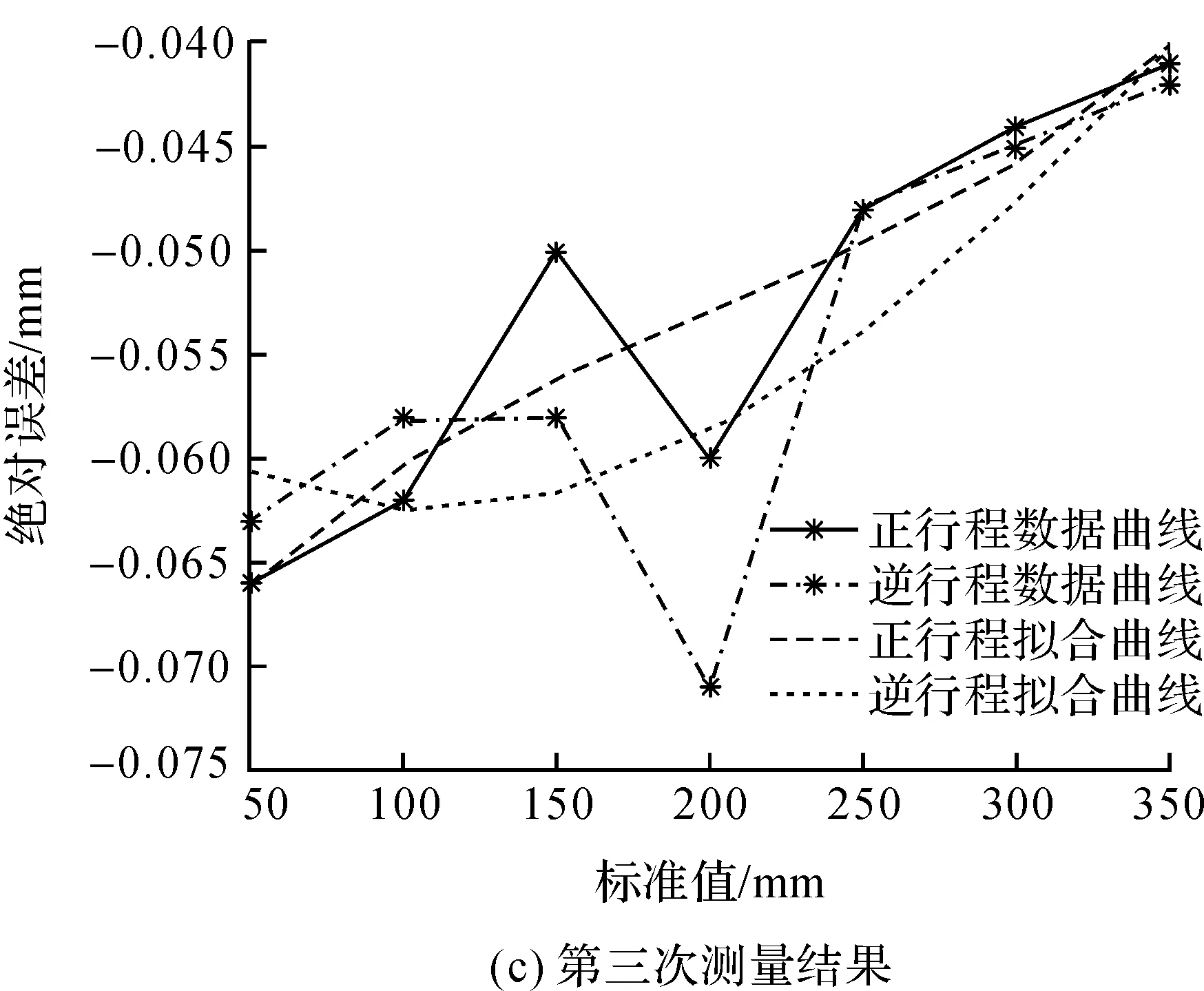
图4 无支架时测量结果Figure 4 Measurement results without scaffold

由于光线折射及水流扰动[9],激光跟踪仪测量的数据存在随机误差，因此可在电离室载台上固定轻质小支架，将靶球托出水面[10]，得到的测量结果如图5.数据结果显示，此时水平轴位移的最大误差平均值为0.29 mm，所有测量点误差的平均值为0.24 mm，各点集的最小拟合函数为

f(x)=-0.0012x+0.122 5.

位移测量系统的基本误差为

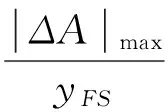
当在载台上粘上小支架后，由于激光跟踪仪的靶球露出水面，因此测量数据的偏差减小了0.611 mm，效果较为显著，测试结果在可接受[11]范围内.但由于小支架自身的重力作用会使悬臂结构[12]的水平轴也产生微小形变，从而引入难以测量的系统误差，因此，此方法仍有待于进一步改进.

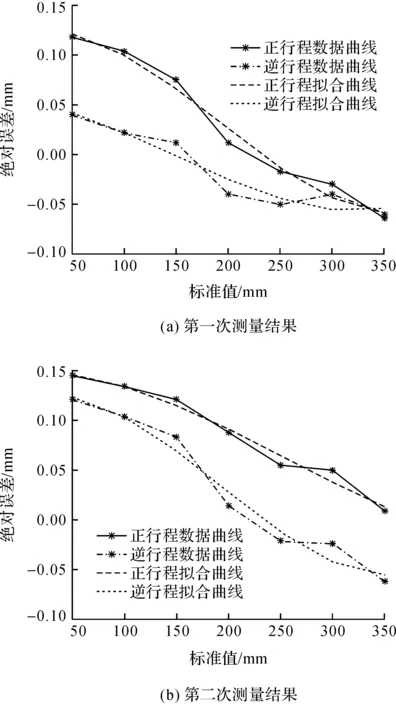
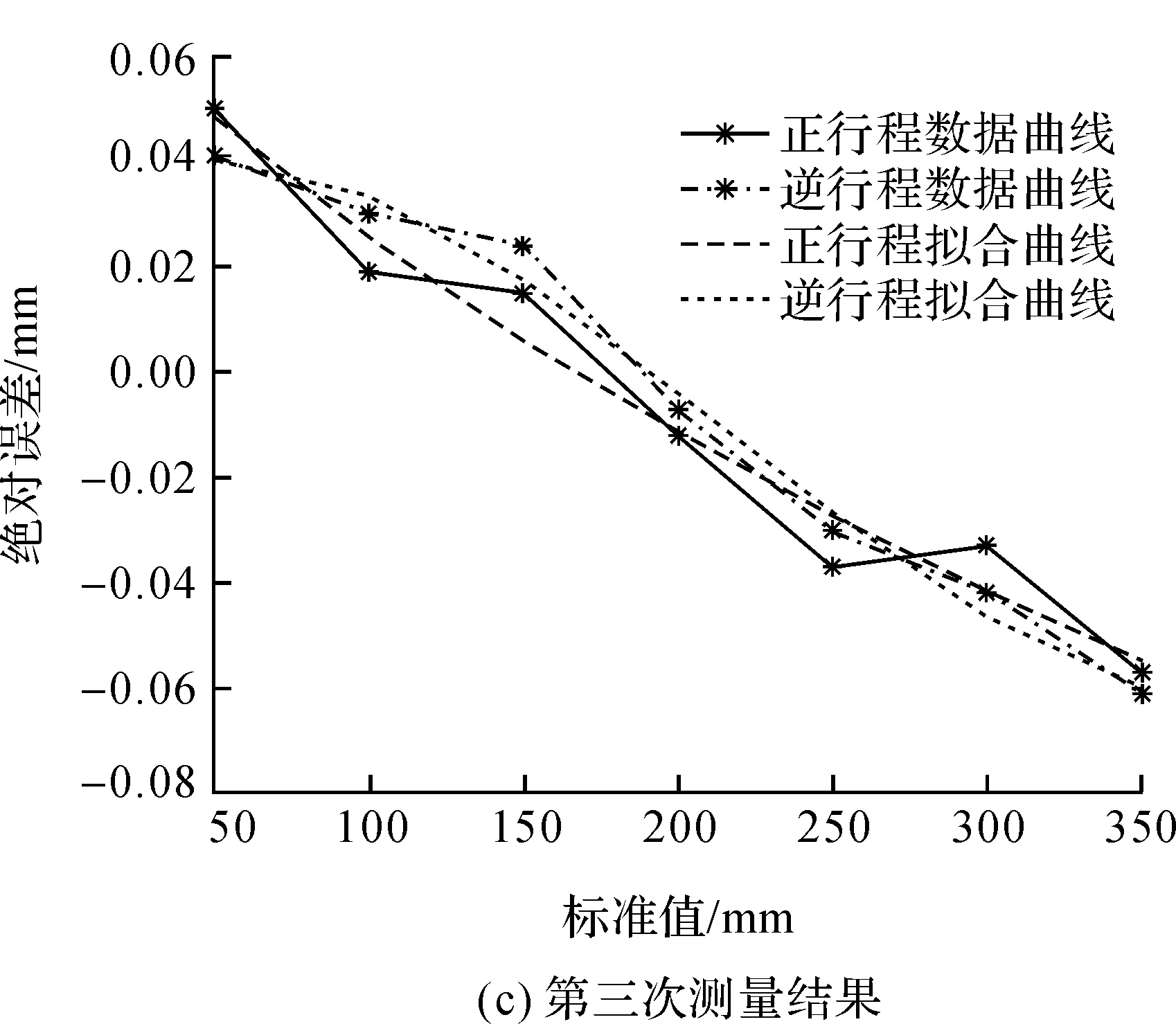
图5 加小支架后测量结果Figure 5 measurements with small stent

4 结 语

本文通过搭建激光跟踪仪测量系统，并引入小支架对射线束分析仪水平轴的定位误差进行测量.在未使用小支架的情况下位移测量系统的基本误差为0.163 6%，利用小支架使激光跟踪仪光束不穿过水箱壁进行测量时，位移测量系统的基本误差为0.061 6%.实验结果表明，利用激光跟踪仪可使射线束分析仪的单轴位移精确度达到0.01 mm精度级，比原有射线束分析仪自身定位精确度(0.1 mm)提高了一个数量级.使用小支架时的基本误差也比不使用小支架时基本误差减小37.65%，实验效果较为显著.

[1] 方超,陈靖,方方,等. 三维水箱运动控制系统的研制[J]. 核电子学与探测技术,2012,30(11):1314-1316. FANG C, CHEN J,FANG F,et al.The development of the 3- d water tank motion control system [J].NuclearElectronics&DetectionTechnology,2012,30(11):1314 -1316.

[2] 赵军,陆首创.基于坐标法的特大齿轮螺旋线偏差计算方法研究[J].中国计量大学学报,2017,28(1):23-28 ZHAO J,LU S C. A coordinate method of spiral deviation of spiral deviation of super-large gears[J].JournalofChinaUniversityofMetrology, 2017,28(1):23-28.

[3] 杨军.影响三维水箱数据采集结果的关键性因素研究[D].北京：清华大学,2015. YANG J.ResearchofKeyFactorsto3-dWaterTankDataAcquisitionResult[D]. Beijing: Tsinghua University, 2015.

[4] 吴湘阳,张坤,常晓斌,等. 三维水箱不同测试条件对数据采集结果的影响和分析[J].现代肿瘤医学，2015，27(22):3322-3326. WU X Y, ZHANG K, CHANG X B, et al. The 3-d water tank under different test conditions on the result of data collection and analysis[J].JournalofModernOncology, 2105,27(22):3322-3326.

[5] 秦宁.基于整体最小二乘面拟合及其在GPS高程拟合的应用研究[D].成都：西南交通大学,2015. QIN N.ResearchofGPSHeightFittingBasedonTotalLeastSquaresSurfaceFittingandApplication[D].Chengdu: Southwest Jiaotong University, 2015.

[6] 胡琳丽,徐志玲,张新娜,等. 刹车片尺寸自动检测装置设计[J]. 中国计量大学学报,2017,28(1):45-50. HU L L,XU Z Z,ZHANG X N, et al. Design of automatic testing devices for brake pad size[J].JournalofChinaUniversityofMetrology, 2017,28(1):45-50.

[7] 樊夏辉,刘桂礼,孔全存,等. 用于微小孔对中的直线约束最小二乘嵌套圆拟合方法[J].制造技术与机床，2017,33(1):133-138. FAN X H, LIU G L, KONG Q C, et al. For use in the tiny hole for nested linear constraint least square circle fitting method[J].ManufacturingTechnology&MachineTool,2017, 33(1):133-138.

[8] 韩庆瑶,肖强,乐英. 空间离散点最小二乘法分段直线拟合的研究[J]. 工业仪表与自动化装置，2012，40(4): 107-109. HAN Q Y, XIAO Q, LE Y. Space discrete points of the piecewise linear fitting of the least-square method [J].IndustrialInstrumentation&Automation, 2012,40(4):107-109.

[9] 周献锋,曹兴江,张乙眉,等. 三维水箱系统和剂量分布仪测量结果[J].中国辐射卫生,2009,18(3):382-383. ZHOU X F, CAO X J, ZHANG Y M, et al. 3-d water tank system and dose distribution measurement result comparison[J].ChineseJournalofRadiologicalHealth, 2009,18(3):382-383.

[10] 匡也. 高精度电感位移传感器校准平台设计[D]. 哈尔滨：哈尔滨工业大学,2016. KUANG Y.DesigningofHighPrecisionInductanceDisplacementSensorCalibrationPlatform[D]. Haerbin: Harbin Institute of Technology,2016.

[11] 李国庆,徐保强,林意群,等. 放疗质量保证工具——三维水箱测量系[J]. 医疗卫生装备,2000,26(4):60-61. LI G Q, XU B Q, LIN Y Q, et al. Radiotherapy quality assurance tools: 3-d water tank measuring system[J].ChineseMedicalEquipmentJournal, 2000,26(4):60-61.

[12] 李国庆,徐保强,林意群. 三维水箱测量系统[J]. 医疗装备,2000,28(4):9-10. LI G Q, XU B Q, LIN Y Q, et al. 3-d water tank measuring system[J].ChineseJournalofMedicalDevice,2000,28 (4):9-10.

Researchoncalibrationofsingle-axisdisplacementprecisionofbeamanalyzers

LI Yunpeng, GUO Tiantai, ZHAO Jun, KONG Ming

(College of Metrology and Measurement Engineering, China Jiliang University, Hangzhou 310018, China)

2096-2835(2017)03-0282-05

10.3969/j.issn.2096-2835.2017.03.003

2107-03-30 《中国计量大学学报》网址zgjl.cbpt.cnki.net

TP216

A