纳米尺度Poiseuille流动中气体黏度的分子动力学研究

陈洁敏，包福兵，凃程旭，尹招琴

(中国计量大学 计量测试工程学院，浙江 杭州 310018)

纳米尺度Poiseuille流动中气体黏度的分子动力学研究

陈洁敏，包福兵，凃程旭，尹招琴

(中国计量大学 计量测试工程学院，浙江 杭州 310018)

受壁面作用和稀薄效应等的影响，微纳尺度通道内的气体流动有别于宏观流动现象. 采用分子动力学方法，研究纳米通道中气体的Poiseuille流动，主要对通道内气体黏度特性进行了分析. 利用牛顿粘性定律，定义了气体的当地等效黏度. 根据模拟结果，可将纳米通道内气体划分为中心区和近壁区两个部分，中心区气体当地黏度与宏观黏度一致，但是在近壁面区，气体受到壁面原子的作用，气体的当地黏度小于宏观黏度值. 研究发现：1)不同的气体密度、流固作用势能以及温度下，通道中心区域的气体当地等效黏度均符合对应温度和压强条件下的气体宏观实测黏度值；2)在纳米尺度气体流动中，气体密度越小，稀薄程度越高，气体偏离热力学平衡态越远，所以壁面对气体等效黏度的影响随密度的减少而增大，壁面影响厚度也随之增大；3)气体黏度的壁面影响厚度在10 nm量级，该厚度不随温度和流固作用势能的变化而变化，但是密度越小，壁面影响厚度越大.

纳米通道；等效黏度；分子动力学；Poiseuille流

Abstract: Due to the effect of wall and rarefaction, gas flow characteristics in nano-scale channels are different from those in macro-scale flow. Gas Poiseuille flows in nano-scale channels were investigated by using the molecular dynamics simulation. The equivalent local viscosity was defined based on the Newton law of viscosity. According to simulation results, the gaseous flow in a nano-scale channel can be divided into two regions, the bulk region and the near-wall region. The equivalent viscosity in the bulk region agrees well with macro value. However, the equivalent viscosity decreases rapidly in the near-wall region. The gas equivalent viscosities always agrees well with macro values at different gas densities, temperatures and gas-wall interactions. In nano-scale channel flows, the wall-influence-depth increases with the decrease of gas density because of the rarefaction effect. The wall-influence-depth is at the order of 10 nm. This depth doesn’t vary with gas temperature and fluid-wall interaction.

Keywords: nano-scale channel flow; equivalent viscosity; molecular dynamics; Poiseuille flow

近些年来，微机电系统和纳机电系统受到了广泛关注，许多微/纳机电系统都涉及到流体的流动[1-3]. 随着特征尺度的变小，流动努森数增大，采用连续介质理论预测的结果与实测结果出现非常大的区别[4-9]，流体流动过程中产生的稀薄效应、滑移效应、热蠕动效应、可压缩效应等特性不能忽略[10-11]，因此迫切需要对纳米尺度下流体的流动特性进行深入研究.

Majumder等人[4]发现，在内径为7 nm的多层碳纳米管流动实验中，实验测得的流量是采用Hagen-Poiseuille公式预测流量的10 000倍左右. Holt等人[5]发现在1.6 nm的碳纳米管中，流体流量比宏观预测值高3个数量级. Whiteby等人[6]研究在内径为40 nm碳纳米管中乙醇、水等流体的输运能力时，发现比宏观值提高了数十倍. 同样， Skoulidas等人[7]和Hummer等人[8]也相继发现碳纳米管中流体的输运能力相比宏观系统得到极大的提高. Joseph等人[9]认为这种引起碳纳米管中流体输运能力提高的原因可能是流体黏度的降低.

黏度是流体的一种宏观性质，其大小是温度和压力的函数. 在传统理论中，黏度值不会随着流体尺度变化而变化. 然而，Bitsanis等人[12]对纳米通道下的Couette流进行模拟，发现在纳米通道中，流体的黏度值与黏度宏观值并不一致. Rowley等人[13]进一步得到了黏度随温度和压强的变化规律. 张晖和张秉坚[14]通过研究通道内氩流体的运动得到了温度、密度和通道高度对流体黏度的影响. Strak和Krukowski[15]发现黏度与压强呈正相关关系. 陈煜和陈硕[16]模拟得到了微通道中超临界氩的黏度和超临界氦的黏度. Prabha和Sathian[17]给出了微通道中黏度与Kn数的关系. 但是上述研究都是针对通道中流体为液体的情况，对气体的研究较少.

骆双双等人[18]研究了在纳米通道气体Couette流的黏度，得到黏度与通道高度的关系，Tu等人[19]进一步得到了气体黏度与温度和密度之间的关系. 而到目前为止关于纳米通道中流体剪切黏度的计算，都是采用速度驱动的Couette流动来实现的，而实际微纳米通道流动大多是由压力驱动的[20]. 压力驱动的纳米尺度流动中气体黏度的研究还非常少，本文主要进行这方面的研究.

1 分子动力学模拟方法

分子动力学方法是一门综合模拟技术，它结合了数学、化学、物理和生物等学科. 用分子动力学方法研究流体黏度的优点在于不需要引入任何常规的假设，直接从原子和分子层面上研究粒子的相互作用，非常适合用于特征尺度小的纳米通道内流体性质的研究.

本文采用分子动力学方法模拟纳米通道中气体的Poiseuille流动. 计算模型示意图如图1，通道高度H设为100 nm，上下壁面均由铂原子组成，按照晶格常数为0.393 nm的FCC晶格排列. 两壁面之间充满氩分子，通过给每个氩分子施加一个x方向的作用力来驱动气体分子运动. 在计算中，上下壁面保持固定，即y方向上采用固定的边界条件，x和z方向均采用周期性边界来代表通道在这两个方向是无限延伸的.

图1 Poiseuille流计算模型示意图Figure 1 Schematic of Poiseuille flow model

在计算中，所有原子间的相互作用势能均采用Lennard-Jones作用势能，因为该势能函数最适合用于惰性气体的模拟：

(1)

其中，rij是两原子之间的距离，ε是势阱深度，σ是原子直径，rc为截断半径. 为了更精确的考虑壁面原子对气体分子的作用，rc统一取为5σAr. 在计算中，εAr=1.653×10-21J，σAr=0.34×10-9m. 氩分子与铂原子之间的势能参数根据Lorentz-Berthelot法则[21]得到εPt-Ar=8.947×10-22J，σPt-Ar=0.31×10-9m. 壁面厚度设置略大于rc来确保壁面对流体作用的准确性.

模拟中，根据邻居列表法得到原子间相互作用力，采用速度标注法控制系统温度以及采用Verlet算法来积分得到原子位置[21]. 时间步长设置为10 fs，模拟共进行了1亿个时间步，前2 000万个时间步是为了系统达到稳定，后8 000万个时间步用来统计相关的宏观物理量. 对于流体密度、剪切速度、剪切应力等宏观量统计时，首先把通道沿y方向按Δy进行分层，本文每层高度设为0.05 nm. 然后统计出每层宏观量的值，最后得到这些宏观量沿y方向的分布.

模拟中，温度设为300 K，气体密度设为8.4 kg/m3，给每个气体分子施加9.72×10-15N的外力. 计算得到气体压强为0.52 MPa和气体平均分子自由程15.35 nm，用通道高度作为特征尺度可得流体流动的努森数约为0.153 5，此时气体处于过渡区.

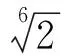
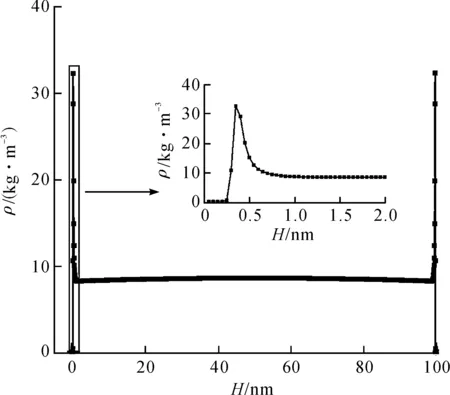
图2 纳米通道中的气体密度分布Figure 2 Gas density profile in the nano-scale channel

从图2中还可以看出，当壁面距离小于0.25 nm时，气体的密度为0. 这是因为在计算中，壁面位置定义在面向通道的第一层铂原子的中心. 当气体分子距离壁面很近时，壁面原子对气体分子的斥力作用非常大，气体在这个斥力作用下远离壁面，所以该区域气体密度为0.

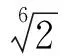
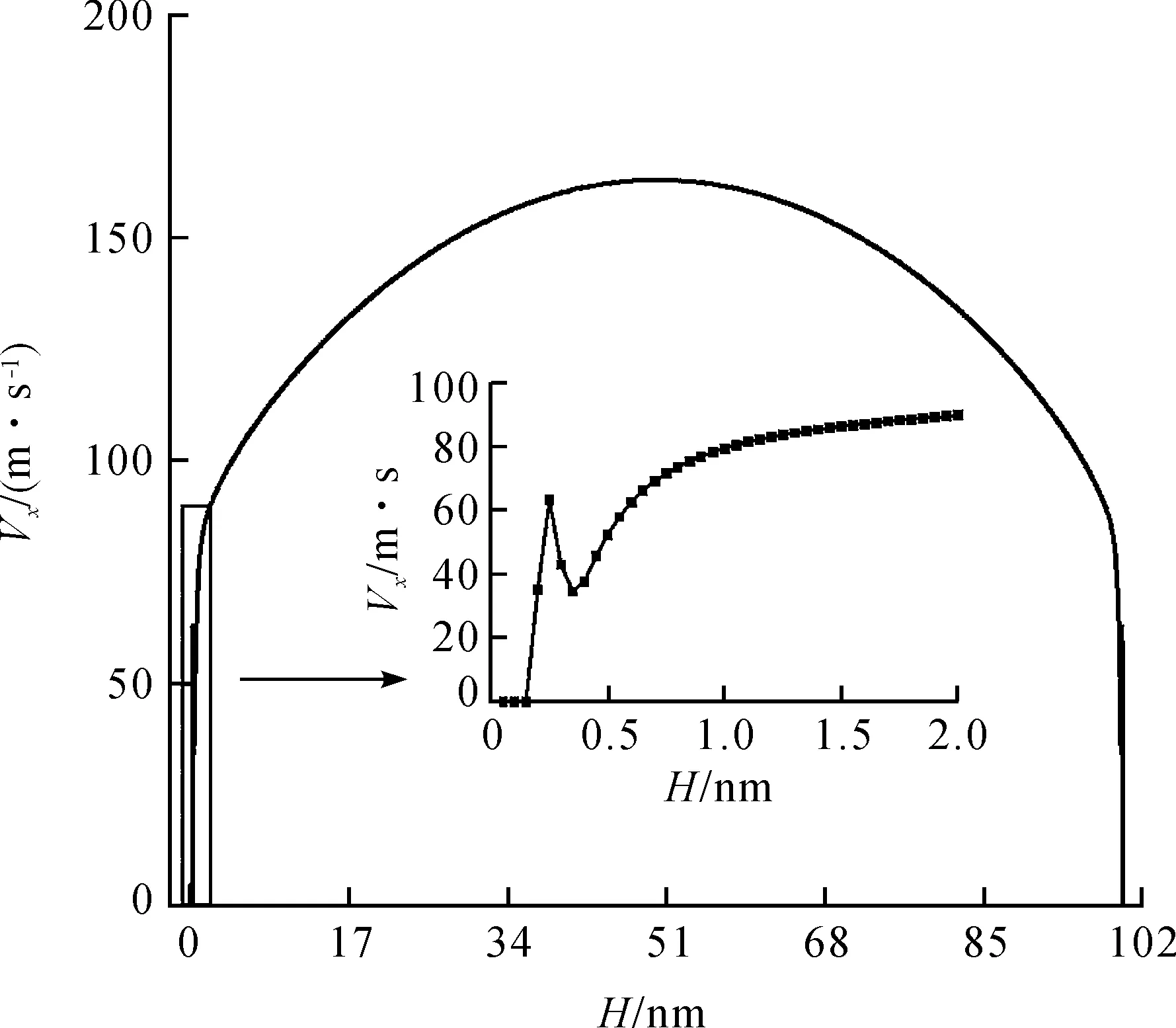
图3 纳米通道中的气体速度分布Figure 3 Gas velocity profile in the nano-scale channel

2 气体黏度的模拟

黏度是流体抵抗速度剪切能力的度量，通常用牛顿粘性定律来表征剪切应力和剪切应变的关系. 在纳米尺度通道流动中，由于通道尺寸小，流动努森数较大，流动属于滑移或者过渡区. 此时，通道的特征尺度与气体平均分子自由程相当或者更小，气体分子相互作用和碰撞较少，偏离了常规尺度下的热力学平衡态. 为了让得到的纳米尺度下的黏度与常规黏度保持一致，根据公式(2)定义纳米通道中流体的等效黏度[22]

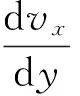
(2)

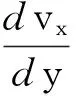
在分子动力学模拟中，气体的剪切应变和剪切应力由气体分子热运动速度计算得到，通过采样获得了不同位置处气体的剪切应变和剪切的分布. 图4给出了通道中气体的剪切应力分量Pxy，从图中可以看出，在通道中心区域，剪切应力分量呈线性分布,与宏观下分布一致. 但是在壁面附近存在较大的波动. 由于壁面原子对气体分子的作用，上下壁面附近分别存在一个极大值和一个极小值.

图4 纳米通道中的气体剪切应力分布Figure 4 Gas shear stress profile in the nano-scale channel

利用不同位置处气体的剪切应变和剪切应力，根据式(2)，可以得到当地的等效黏度值，图5给出了纳米尺度通道中气体的当地等效黏度分布. 图5中同时给出了同一温度和压强下氩的宏观黏度值. 从图中可以看出，在通道中心区域，采用分子动力学方法计算得到的黏度值与客观真实值[23]符合得非常好. 但是，由于在分子动力学模拟中，速度值是由气体分子的热运动速度统计得到的，速度大小存在一定的波动. 虽然在计算中，采用了8 000万步的结果来做统计，得到的速度分布比较均匀，如图3，但是在求速度梯度时，波动仍旧比较大. 特别是在通道中心区域，速度剖面计较平坦，速度梯度比较小，从而波动较大.

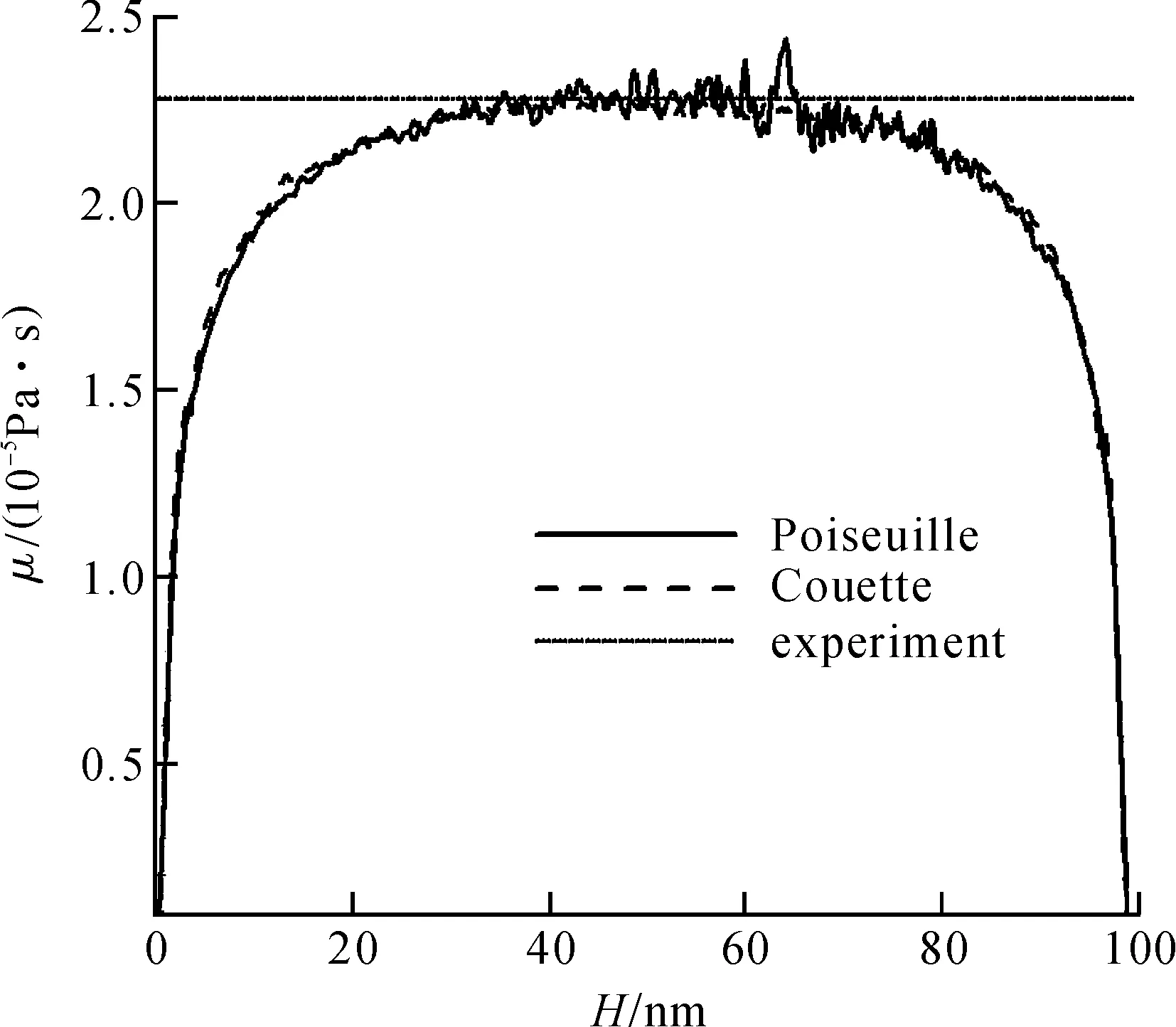
图5 纳米通道中的气体当地等效黏度分布Figure 5 Local equivalent viscosity profile in the nano-scale channel

在靠近壁面时，当地黏度出现较大变化. 气体的当地等效黏度值随着与壁面距离的减小而减小. 可以把通道分为中心区和近壁区两个区域，在中心区气体黏度与宏观黏度保持一致；当气体分子处于近壁区，此时气体黏度小于宏观黏度. 从图中可以看出，壁面影响厚度大概在30 nm左右，远大于速度和剪切应力的影响范围. 当通道高度H很大时，壁面影响厚度可以忽略，气体黏度等同于宏观黏度. 但是，随着通道高度的减小，近壁区的黏度影响就不可忽略. 在直径从几纳米到几十纳米[4-8]的碳纳米管流动中，流体均处在于近壁区，所以流体的平均黏度远小于宏观黏度，所以造成了质量流率的增加.

图5中也给出了Tu等人[19]采用Couette流动计算得到等效黏度分布. 在计算中，通道高度、气体密度、温度和压力保持一致. 从图中可以看出，采用两种方法计算得到的当地等效黏度值符合得非常好. 这也从另一个侧面证明了本文采用方法的正确性. 相比于Couette流动，在计算步数相同的情况下，由于Poiseuille流动中心线附近较小的速度梯度，采用Poiseuille流动计算得到的等效黏度值波动较大.

3 纳米通道中气体的等效黏度

3.1 气体密度对黏度的影响

本文首先研究了不同密度下纳米通道中气体的当地等效黏度的特性. 考虑了4种密度的影响(ρ=8.40 kg/m3，13.44 kg/m3，16.80 kg/m3和21.84 kg/m3)，其他参数与前面保持一致.

不同密度时，等效黏度在通道内的分布与图5类似. 中心区域黏度与宏观黏度值符合得很好，但在近壁区，不同密度下存在较大区别. 图6是壁面附近气体等效黏度在不同密度下的分布. 由图可得，距离壁面一定高度时，即达到了中心区，气体的当地等效黏度与密度便不再相关，等效黏度值相等且与实验值吻合. 而在近壁区，密度越小，单位体积内的气体分子数越少，气体分子之间相互碰撞概率就越小，从而气体稀薄程度越高，偏离热力学平衡态也越大. 因此，通道内的气体密度越小，壁面对气体分子影响力越大，壁面影响厚度也越大. 如图6，ρ=21.84 kg/m3时，当距离壁面9 nm左右，气体的当地等效黏度就已经趋近于宏观黏度值，说明此时的壁面影响厚度在9 nm左右. 而当ρ=8.40 kg/m3时，壁面影响厚度达到30 nm左右.

图7是壁面影响厚度随气体密度变化的分布图. 从图中可得到壁面影响厚度随着密度的增大而减少。

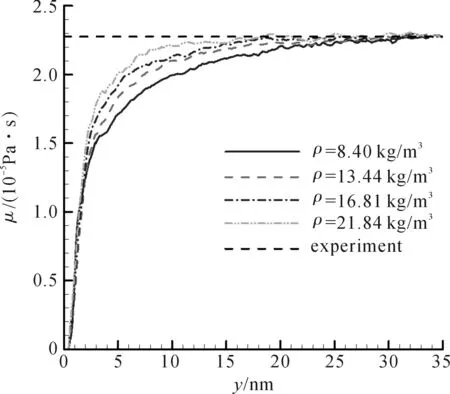
图6 不同气体密度时等效黏度在壁面附近的分布Figure 6 Profiles of equivalent viscosity near the wall at different gas densities

图7 壁面影响厚度随气体密度的变化Figure 7 Variation of wall thickness with gas density

3.2 流固作用势能对流体黏度的影响

由于壁面的存在，壁面附近的气体运动特性发生变化. 壁面与气体原子流固作用势能是否气体流动有影响是本小节研究的目的. 通过改变流固作用势能的参数ε来改变流固作用强度. 本文中共考虑了四种势能参数，ε=0.66×10-21J，1.65×10-21J，3.31×10-21J和4.96×10-21J，其他参数与前面保持一致.

从模拟结果可以发现，不同流固作用势能对通道中心区域的气体等效黏度没有影响，中心区域的气体黏度值始终与宏观黏度值一致. 图8给出了4种流-固作用强度下壁面附近当地等效黏度的分布. 从图中可以发现，不同的流固作用势能强度对壁面附近的气体黏度分布影响不大. 虽然不同流固作用势能强度会影响壁面附近的气体密度峰值，但是对气体的当地黏度分布几乎没有影响，因此壁面影响厚度不随着流固作用势能的变化而变化.

3.3 温度对流体黏度的影响

温度是影响流体黏度的另一个重要因素，本小节采用T=200 K，300 K，400 K和500 K四种温度研究温度气体黏度的影响，其他参数与前面保持一致.

图9给出了不同温度下通道中心区域等效黏度值与宏观黏度值的比较. 对于气体而言，随着温度的升高，气体分子的热运动加剧，热运动速度增加，气体分子更容易从一个区域迁移到另外一个区域，越容易与其他分子碰撞，从而动量交换越频繁，使流体间层与层之间的内摩擦加剧，黏度值也不断增大. 从模拟的结果来看，随着温度的升高，气体等效黏度也不断增大，该模拟结果与实验结果符合良好.

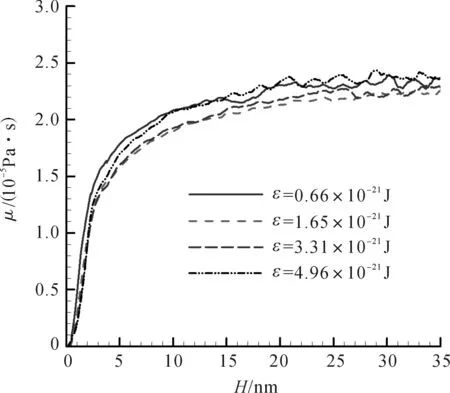
图8 不同壁面作用下气体的等效黏度在壁面附近的分布Figure 8 Profiles of gas equivalent viscosity near the wall at different wall actions

图9 通道中心区域的气体等效黏度随温度的变化Figure 9 Variation of gas equivalent viscosity with temperature in the bulk region

图10是壁面附近气体当地等效黏度在不同温度下的分布. 由图可得，气体的等效黏度随温度的增大而增大. 但是，不同温度下，固体壁面对气体黏度的影响范围比较一致，所以壁面影响厚度不随温度的变化而变化.

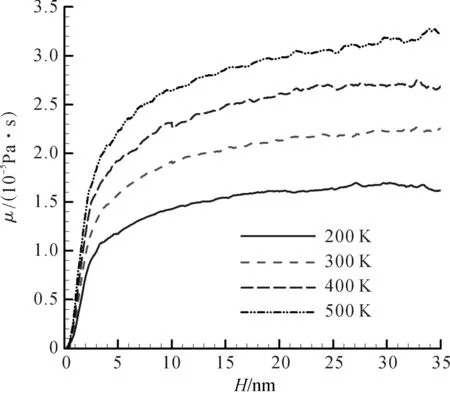
图10 不同温度下气体的等效黏度在壁面附近的分布Figure 10 Profiles of gas equivalent viscosity near the wall at different temperatures

4 结论与展望

本文采用分子动力学方法，研究了纳米尺度通道中气体Poiseuille流动. 又根据牛顿粘性定律，对气体在纳米通道内的当地等效黏度进行了定义. 研究表明，纳米通道中气体的当地黏度不再像宏观黏度那样分布均匀，比较通道中的黏度可以把通道分为中心区和近壁区两个区域，在中心区域气体的等效黏度与宏观黏度保持一致，证明了等效黏度定义的可行性. 但在近壁区，由于壁面原子对气体分子的作用，气体的当地黏度迅速降低.

接着，研究了不同的气体密度、不同流固作用势能以及不同气体温度对纳米尺度气体黏度的影响，得到了在中心区域当地等效黏度与气体宏观实测值保持一致.但对于壁面附近，气体密度越小，壁面对气体等效黏度影响越大，壁面影响厚度也越大，并且壁面影响厚度与温度和流固作用势能的大小无关.

[1] GAD-EL-HAK M.MEMS:IntroductionandFundamentas[M]. Boca Raton: CRC Press, 2010:128-141.

[2] LYSHEVSKI S E.Nano-andMicro-ElectromechanicalSystems:FundamentalsofNano-andMicroengineering[M]. Boca Raton: CRC press, 2005:211-215.

[3] 余霞, 包福兵, 毛志红. 二元混合物气液相变特性的分子动力学研究[J]. 中国计量学院学报, 2012, 23(3): 289-294. YU X, BAO F B, MAO Z H. Molecular dynamics simulation of vapor-liquid transition characteristics of binary mixture[J].JournalofChinaUniversityofMetrology,2012,23(3):289-294.

[4] MAJUMDER M, CHOPRA N, ANDREWS R, et al. Nanoscale hydrodynamics: Enhanced flow in carbon nanotubes[J].Nature,2005, 438(3): 44-46.

[5] HOLT J K, PARK H G, WANG Y, et al. Fast mass transport through sub-2-nanometer carbon nanotubes[J].Science, 2006, 312(8): 1034-1037.

[6] WHITBY M, QUIRKE N. Fluid flow in carbon nanotubes and nanopipes[J].NatureNanotechnology, 2007, 2(2): 87-94.

[7] SKOULIDAS A I, ACKERMAN D M, JOHNSON J K, et al. Rapid transport of gases in carbon nanotubes[J].PhysicalReviewLetters, 2002, 89(18): 1-4.

[8] HUMMER G, RASAIAH J C, NOWORYTA J P. Water conduction through the hydrophobic channel of a carbon nanotube[J].Nature, 2001, 414(12): 188-190.

[9] JOSEPH S, ALURU N R. Why are carbon nanotubes fast transporters of water?[J].NanoLetters, 2008, 8(2): 452-458.

[10] 包福兵. 微纳尺度气体流动和传热的Burnett方程研究[D]. 杭州: 浙江大学, 2008. BAO F B.BurnettSimulationofMicro-andNanoscaleGasFlowandHeatTransfer[D]. Hangzhou: Zhejiang University, 2008.

[11] 骆双双. 微纳通道中流体黏度特性的分子动力学研究[D]. 杭州: 中国计量大学，2015. LUO S S.MolecularDynamicsStudiesofFuildViscositiesinMicro/nano-scaleChannels[D]. Hangzhou: China Jiliang University, 2015.

[12] BITSANIS I, VANDERLICK T, TIRRELL M, et al. A tractable molecular theory of flow in strongly inhomogeneous fluids[J].TheJournalofChemicalPhysics, 1988, 89(5): 3152-3162.

[13] ROWLEY R L, PAINTER M M. Diffusion and viscosity equations of state for a Lennard-Jones fluid obtained from molecular dynamics simulations[J].Internationaljournalofthermophysics, 1997, 18(5): 1109-1121.

[14] 张晖, 张秉坚. 微孔中简单流体黏度的分子动力学模型及关联模型[J]. 物理化学学报, 2003, 19(4): 352-355. ZHANG H, ZHANG B J. Molecular dynamics simulation and correlation model of simple fluid viscosity in micropores[J].ActaPhysicaSinica,2003, 19(4): 352-355.

[15] STRAK P, KRUKOWSKI S. Molecular dynamic simulations of viscosity of argon at high pressures[J].HighPressureResearch, 2008, 28(4): 469-476.

[16] 陈煜, 陈硕, 巨永林，等. 超临界L-J流体黏度的分子动力学模拟[J]. 低温工程, 2008，29(4): 32-37. CHEN Y, CHEN S, JU Y L, et al. Molecular dynamics simulation of viscosities for supercritical L-J fluids[J].Cryogenics, 2008，129(4): 32-37.

[17] PRABHA S K, SATHIAN S P. Molecular-dynamics study of poiseuille flow in a nanochannel and calculation of energy and momentum accommodation coefficients[J].PhysicalReviewE, 2012, 85(4): 201-203.

[18] 骆双双, 包福兵, 林建忠. 纳米尺度通道中气体黏度的分子动力学模拟[J]. 低温工程, 2015，36(2):28-32. LUO S S, BAO F B, LIN J Z. Molecular dynamics simulation of gas viscosity in nano-scale channels[J].Cryogenics, 2015，36(2):28-32.

[19] TU C X, QIAN L J, BAO F B, et al. Local effective viscosity of gas in nano-scale channels[J].EuropeanJournalofMechanics-B/Fluids, 2017,64(2):55-59.

[20] 刘彬武, 刘朝, 刘娟芳. 微通道中Poiseuille流动的分子动力学研究[EB/OL].(2017-06-20) [2007-07-06]. http://www.paper.edu.cn/releasepaper/content/200707-132. LIU B W, LIU C, LIU J F. Study of molecular dynamic simulation of Poiseuille flow in a microchannel[EB/OL].(2017-06-20) [2007-07-06]. http://www.paper.edu.cn/releasepaper/content/200707-132.

[21] RAPAPORT D C.TheArtofMolecularDynamicsSimulation[M]. Cambridge :Cambridge University Press, 2004:38-48.

[22] ALLEN M P, TILDESLEY D J, BANAVAR J R. Computer simulation of liquids[J].PhysicsToday, 1989, 18(1)：105-108.

[23] 黄永华, 陈国邦. 低温流体热物理性质[M].北京： 国防工业出版社, 2014：336-341.

Moleculardynamicssimulationofgasviscosityinnano-scalePoiseuilleflow

CHEN Jiemin, BAO Fubing, TU Chengxu, YIN Zhaoqin

(College of Metrology and Measurement Engineering, China Jiliang University, Hangzhou 310018, China)

2096-2835(2017)03-0293-07

10.3969/j.issn.2096-2835.2017.03.005

2017-06-26 《中国计量大学学报》网址zgjl.cbpt.cnki.net

国家自然科学基金资助项目(No. 11372298, 11672284)，国家重点研发技术重点专项项目(No.2017YFB0603701).

O357

A