太阳影子定位有关研究
2017-09-30鲁晓晓王子延
鲁晓晓,王子延
太阳影子定位有关研究
鲁晓晓1,王子延2
(1.火箭军武汉指挥学院,武汉 430012;2.火箭军工程大学,西安 710025)
分析视频中物体的太阳影子变化,来确定视频拍摄的地点和日期。首先对视频进行处理,得出各时间点的像素,通过影长的像素和直杆的像素的对比,得出影子长度,其次确定影响影子长度的变化的各种因素,通过对影子形成原因的分析,初步确定影响影子长度变化最主要的因素为直杆的长度、太阳高度角这两个因素。利用几何关系和各因素的定义,可以推导出影响影子长度变化的函数关系式。结合数据确定约束条件,利用最小二乘的思想,建立以影子长度偏差最小和影子角度偏差最小为目标的多目标非线性规划模型。通过搜索算法,编写MATLAB程序,得出各时间点的经纬度。经过检验和优化之后,确定最优解并得出若干个可能地点。
影子长度;太阳高度角;多目标非线性规划;视频处理
0 引言
如何确定视频的拍摄地点和拍摄日期是视频数据分析的重要方面,太阳影子定位技术就是通过分析视频中物体的太阳影子变化,确定视频拍摄的地点和日期的一种方法。下面我们就介绍太阳影子定位方法。
1 建立影子长度模型
影子是一种光学现象,其产生主要与太阳和直杆有关,故影子长度的变化也与二者有关。影子长度与太阳、直杆的关系如图1所示。

图1 影子长度与太阳、直杆的关系

其中,L代表是直杆的高度,h代表的是太阳高度角。
(1)太阳高度角的计算
从式(1)中可以看出,在直杆的高度一定的情况下,影子长度主要与太阳高度角有关。太阳高度角的一般计算方法如下式所示:

在分析上图后,可得出影子长度l的函数式为:
式中φ、λ为计算地点的地理经纬度,t为北京时间,δ为太阳赤纬。但由于太阳赤纬的变化并不均匀,且相对运算较为繁琐,而太阳黄经的变化是均匀的,可以利用太阳黄经来代替太阳赤纬。两者之间的关系为:

式中ξ为黄赤交角,等于23°27',λ'表示太阳黄经,太阳在一年中沿黄经走一圈,零度在春分点上,其速度是均匀的。设每日所走的度数为λ''则:
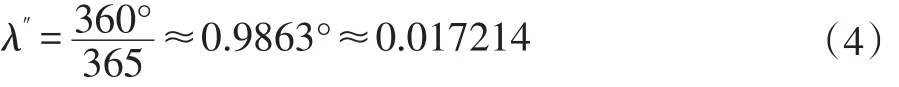
那么某日的太阳赤纬满足关系:

式中T为刻日距春分日的天数。
为方便计算任意月份的太阳高度角,现给出下表,表中4-12表示4-12月份,13-15表示1-3月份。
2 视频拍摄定位分析
2.1 视频中影长确定

表1 各月第一天距春分日的天数
则T=DM+d,这里的d表示为M月份中的某日期数。
(2)太阳方位角的计算
太阳方位角是指照射到目标物的太阳光线在地平面上的投影与目标物所在点的子午线(即目标物的正北方向)的夹角,即从目标物所在点的子午线按顺时针方向到太阳光线投影的夹角,其取值范围是0~360°。太阳方位角的计算可分为3步:
①计算太阳赤纬角δ。太阳赤纬角是地球赤道平面与太阳和地球中心连线之间的夹角实际际上就是太阳和地球中心的连线与南北极极轴夹角的余角(这是因为极轴垂直于赤道平面)。赤纬角以年为周期,取值范围是[-23 °27′,+23 °27′]。赤纬角δ的计算公式为:
sinδ=sinξsinTλ''
②计算太阳高度角α。
③太阳方位角A的计算如下:

利用Photoshop软件对视频进行截屏处理,平均每三分钟进行一次截屏,共截屏14次,得到14张截屏图片。在Photoshop中将14张图片依次进行像素处理,在得到像素图片后,计算从影子顶点到直杆底部的像素差和直杆顶端到底端的像素差。在得知杆长为两米的的情况下,将两次像素差作比,便可得出影子的长度。
2.2 确定决策变量
根据某固定实物在水平地面上的太阳影子顶点坐标数据,建立数学模型确定实物所处的地点和日期,所以日期成为变量。确定该模型的决策变量为其它的几个变量即经度λ,纬度φ和杆长L,以及测量日期距春分日的天数T。
2.3 确定目标函数
所给时间为12:41到13:41,由影长逐渐变长可知进入了下午,北京经度为东经116°,可知测量地点距北京向东不会超过15°经度,即东经131°。而测量地点不可能为傍晚,可知向西不会超过60°,即东经56°。则其经度、杆长、太阳赤纬以及天数的约束范围如下:
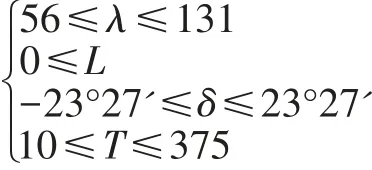
(2)影子长度模型建立
由此,就可计算任意时间地点的太阳高度角,并且利用太阳高度角,即可求出影子长度l。由此便可得出影子长度变化的数学模型为公式(8)。

为检验所得的影长与实际影长是否相符,将所得影长数据累加与根据原数据所得的影长的累加作差,为便于比较,利用差值的平方,当该平方值小于某一很小的正数ε时即可认为该影长与实际相符,如公式(9)。
2.4 优化模型
因为本题范围在中国范围内,并且太阳赤纬角及实物高度都有各自的限度,所以给出的目标函数和约束条件如公式(10)。

3 实验验证
首先我们将2015年7月13日在内蒙古自治区上默特右旗拍摄的视频(如图2)进行分解,每隔3分钟取一张图片,运用Photoshop软件测量像素,确定实物和影长的比例。图中的杆长l已知,从而得到14组时刻影子的长度。

图2 视频每3分钟取一副单帧图像

表2 视频中数据的处理与运算
通过对视频的处理,得到了视频中影子的长度,再根据视频中所现实的信息可以得出T=124,杆长已知为2米。之后将这些数据代入问题二中所建立的模型,得出各时间点经纬度,通过检验和优化之后,得出最优解。利用这个最优解,可以大致推算出其拍摄地点,如表3所示。
第二问就是如果拍摄时间未知,即T未知,在只知道杆长和影长的情况之下求出拍摄地点和拍摄时间。利用第三问中所建立的模型,将影长和杆长的数据代入之后,计算出各时间点的经纬度和拍摄日期。经过检验和优化之后,确定最优解,其结果如表4。
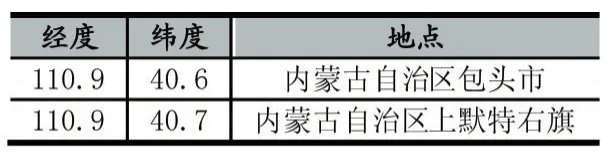
表3 拍摄地点

表4 根据视频预测的结果
由于太阳赤纬表达式为三角函数,存在距春分日天数不同时结果相同的情况,所以仅由杆长和影长不能准确判断日期和地点,需要结合视频中的其他信息,如风速,光强,植物特征等判断拍摄的季节,进而推断出拍摄的地点,得出最终结论。
4 讨论
模型优点:
(1)本模型充分考虑了影子形成的主要因素:杆长和太阳高度角,并考虑了太阳方位角所带来的影响因素,考虑因素全面,具有代表性。
(2)模型的可扩展性强,本文可以通过已知的一两个条件,计算出其他的待测条件。但出现新的问题之后,代入模型即可进行计算和解答,适用面广。
不足之处:
(1)在数据处理过程中存在着误差,对计算结果有一定的影响,使计算结果出现一定的偏差。
(2)在处理影响因素的过程中,忽略了许多次要因素,只考虑了主要因素,其结果会有一定的误差。
[1]陈健婷,温银婷,傅守忠.最佳太阳方位角的计算[J].肇庆学院学报,2014,35(2).
[2]易海涛.环保工作中太阳高度角的简便计算[J].环境科学与技术,第32期
[3]李玉海.太阳高度角及其计算[J].
[4]占海明.基于MATLAB的高等数学问题求解[M].北京:高等教育出版社,1993.
Identify Geographical Location from Sun Shadow
LU Xiao-xiao1,WANG Zi-yan2
(1.The Rocket Army Command College,Wuhan 430012;2.Rocket Force University of Engineering,Xian 710025)
Analyzes the changes in the sun shadow of objects in the video to determine the location and date of the video.First,the video processing,the pixels at each time point,through the shadow of the pixels and straight pixels of the contrast,the shadow length,and then determine the shadow changes in the length of the various factors,through the shadow of the formation of the reasons Analysis,preliminary determine the impact of shadow length changes in the main factors for the length of the straight rod,the sun height angle of these two factors.Using the definition of geometric relation and each factor,we can deduce the function relation which affects the change of shadow length.Based on the data,the multi-objective nonlinear programming model with minimum shadow length deviation and shadow angle deviation is estab⁃lished by using the least squares idea.Through the search algorithm,write MATLAB program,obtained at each time point of latitude and longitude.After the test and optimization,the optimal solution is determined and a number of possible locations are obtained.
Shadow Length;Solar Elevation Angle;Multiobjective Nonlinear Programming;Video Processing
1007-1423(2017)24-0003-04
10.3969/j.issn.1007-1423.2017.24.001
鲁晓晓(1990-),女,河北沧州人,学生,研究方向为信息与通信工程
王子延(1994-),男,河北廊坊人,学生,研究方向为信息与通信工程
2017-05-16
2017-08-05
