利用相似形解决影子问题

田静（贵州兴义八中）

利用相似形解决影子问题

田静
（贵州兴义八中）

在光线的照射下物体会留下“影子”，下面结合例题谈谈阳光下的影子和灯光下的影子问题，供同学们学习参考.

一、阳光下的影子

阳光下的影子是太阳光线形成的，由于太阳离我们非常遥远，所以我们可以把太阳光线看成平行光线.

1．影子全落在地面上

例1.某天同时同地，甲同学测得1米的测竿在地面上影长为0.8米，乙同学测得国旗旗杆在地面上的影长为9.6米，则国旗旗杆的高为（）

A．10米B．12米C．13米D．15米

分析：在同时同地的条件下，物体和它在地面上的影长成正比，因此，于是可得

1∶0.8=x∶9.6易求得旗杆高x为12米，故选B．

2．影子有一部分落在墙上

例2.张明同学想利用树影测校园内的树AB高.他在某一时刻测得小树高为1.5米，其影长为1.2米.当他测量教学楼旁的一棵大树影长时，因大树靠近教学楼，有一部分影子落在了墙上.经测量，地面部分影长BC为6.4米，墙上影长CD为1.4米，那么这棵大树高约____米.

分析：影子BC所对应的物高与墙上的影长CD的和即是大树的高，如图1所示，易求得影子BC所对应的物高为8米，所以大树高为9.4米.四边形AECD为平行四边形，所以影长CD=物高AE，AB=AE+BE=8米+1.4米=9.4米.

图1

针对训练1：（影子落在竖直的墙壁上）赵亮同学想利用影长测量学校旗杆的高度，如图2，他在某一时刻立1米长的标杆测得其影长为1.2米，同时旗杆的投影一部分在地面上，另一部分在某一建筑的墙上，分别测得其长度为9.6米和2米，则学校旗杆的高度为______米．

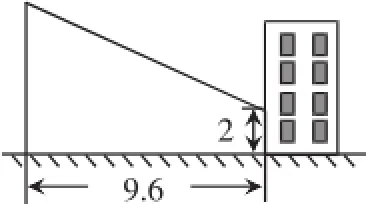
图2

3．影子有一部分落在斜坡上

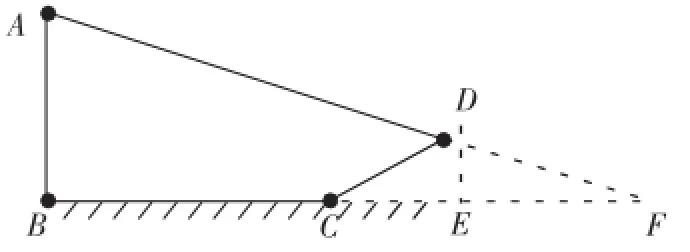
图3

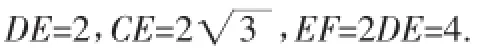
针对训练2：（影子落在斜坡上）如图4，小明想测量电线杆AB的高度，发现电线杆的影子恰好落在土坡的坡面CD和地面BC上，量得CD=4厘米，BC=10厘米，CD与地面成30°的角，且此时测得1米杆的影长为2米，则电线杆的高度为_____米.

所以

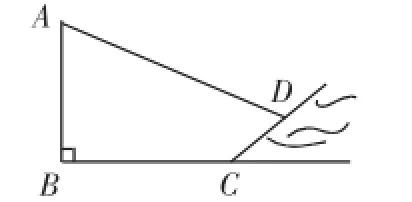
图4

小结：在同一时刻，物高与影长成正比.所以，先测量木杆和其影长，然后测量建筑物的影长（影子在地面、在斜坡、在墙上等等），利用同一时刻物高与影长成正比这一比值便可以求出物高来（如旗杆高、楼房高……）

二、灯光下的影子

与阳光相比，灯光光线对我们来说是近距离而不平行、四射的，而且同一物体对于同一光源在不同的地点影长也不相同．

例4.一位同学身高米1.6，晚上站在路灯下A处，他在地面上的影长AB=2米，若他沿着影长的方向移动2米站立B处时，影长BC为2.5米，求路灯的高度．

析解：设路灯高为x米，人高为y米，如图5所示，当人在A点时，影长AB=2米，当人在B点时，影长BC为2.5米，由于△COE∽△CBD，△BOE∽△BAF

由（1），（2）式易求得x=8．即，路灯的高度为8米．

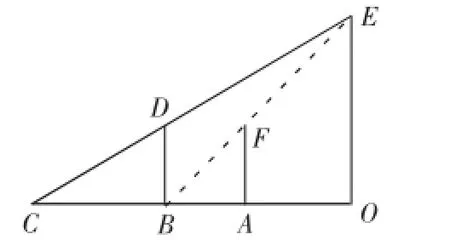
图5

小结：人站在灯光下不同的位置，构造出不同的直角三角形，利用相似三角形中边的比例关系，便可以求出物高。

针对训练习3：如图6，有一路灯杆AB（底部B不能直接到达），在灯光下，小明在点D处测得自己的影长DF＝3米，沿BD方向到达点F处再测得自己的影长FG＝4米，如果小明的身高为1.6米，求路灯杆AB的高度。

图6

针对训练答案：

·编辑鲁翠红