一种新的MQ径向基函数拟插值格式

张继红，王瑞林

(大连交通大学 理学院，辽宁 大连 116028)*

一种新的MQ径向基函数拟插值格式

张继红，王瑞林

(大连交通大学 理学院，辽宁 大连 116028)*

提出了一种新的MQ径向基函数拟插值算法，给出了该格式的构造原理及其性质，并用它来逼近函数.通过数值算例及与真实值的对比，验证了所提方法的有效性.提出的方法形式简单，不需要求解任何线性方程组，容易实现，且具有不错的逼近效果.

MQ径向基函数；拟插值格式；数值逼近

0 引言

径向基函数是处理多元问题的一种有效的方法.实质上，它是通过定义在[0,+∞)上的一元函数φ与Rd上的欧几里德范数‖·‖2来表示d元函数φ(‖x-y‖2),其中x,y∈Rd，径向基函数在数据拟合方面更是有着形式简单和精度高等优点.常见的径向基函数有Kriging方法的Gauss分布函数和Markov分布函数及Hardy的MQ函数，而MQ径向基函数作为数值性能最好的方法之一在数学领域受到了广泛的关注.

在逼近论及其应用中拟插值格式是一个非常用力的工具，能够避免插值问题所要面临的求解大量线性方程组以及由此产生的病态问题.MQ径向基拟插值最早是由Beaston和Powell[1]在1992年提出的，他们给出了三种单变量MQ拟插值算子，分别叫LALB和LC，1994年Wu和Schaback[2]提出单变量的MQ拟插值算子LD，并且证明了这种格式有保形并且收敛.2009年Wu和Ma[3]构建了新的MQ拟插值算子LE成功应用到了Sine-Gordon方程中.

本文提出一个新的MQ拟插值算子.具体安排如下：首先介绍MQ拟插值格式的构造及其性质，然后用三个数值实验来验证这种方法的可行性，最后给出文章的结论及未来的工作方向.

1 MQ径向基拟插值格式的构造及其性质

定义1 给出径向基拟插值算子LN的如下表达式：

其中,

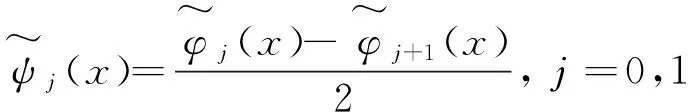
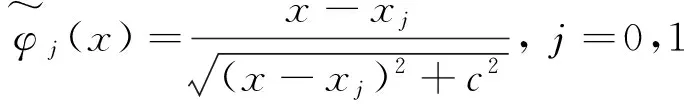
1.1 MQ拟插值格式的构造原理

考虑

以及

那么

假设

则有

考虑

用左矩形公式近似积分：

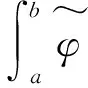
因此

1.2 公式的性质

可以证明LN具有保常数性和保单调性.

定理1LN保常数性.

证明：令f(x)=1,则格式LNf(x)=1，很容易被验证.

定理2LN具有保单调性.

证明： 等式(1)的一阶导数如下：

因为

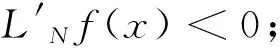
2 数值实验

通过数值算例给出该MQ拟插值格式对函数的数值近似情况，用三个算例来验证方法的有效性.首先考虑函数f(x)=arctan5x,0≤x≤1,取数据点为区间[0,1]间的均匀节点，步长h=0.001,给出真实值和LNf近似函数的对比图像及绝对误差图像，分别如图1、图2所示.

图1 真实值与近似值对比图图2 真实值与近似值 的绝对误差图

考虑函数f(x)=ex3+cos2x,0≤x≤1,取数据点为区间[0,1]间的均匀节点，步长h=0.001,其真实值和LNf近似函数的对比图像及其误差图像，分别如图3、图4所示.

图3 真实值与近似值对比图 图4 真实值与近似值 的绝对误差图

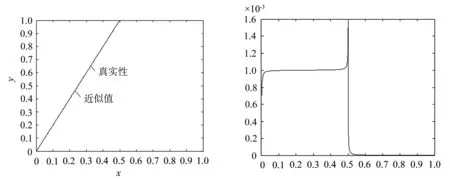
图5 真实值与近似值对比图 图6 真实值与近似值 的绝对误差图

通过以上三个算例中，真实值和近似值的对比情况，可以看出这个方法是可行的，更重要的是该方法是显示表达式，不需要求解线性方程组，格式简单，易于编程实现.

3 结论

本文构造了一种新的MQ径向基拟插值算法，给出了格式的构造原理及性质，并且通过数值实验对函数进行数值逼近，得到了比较好的数值结果.数值算例验证了本文所提算法的有效性，本算法最大特点在于形式简单，不用求解线性方程组，避免了病态问题，易于编程实现，并且具有不错的近似效果.该方法在微分方程数值解中的应用，是我们未来的研究方向.

[1]BEATSON RK,POWELL MJD.Univariate multiquadric approximation:quasi-interpolation to scattered data[J].Construct Approx,1991(8):275- 288.

[2]WU Z M,SCHABACK R.Shape preserving properties and convergence of univariate multiquadric quasi-interpolation[J].Acta Math.Appl Sinica,1994,10(4):441- 446.

[3]MA LM,WU ZM.A numerical method for one-dimensional nonlinear Sine-Gordon equation using multi-quadric quasi-interpolation[J].Chinese Phys B，2009,18(8):3099- 4005.

[4]吴宗敏.散乱数据拟合的模型、方法和理论[M].北京：科学出版社，2007.

A New MQ Radial Basis Function Quasi-Interpolation Scheme

ZHANG Jihong,WANG Ruilin

(School of Mathematics and Physics,Dalian Jiaotong University,Dalian 116028,China)

In this paper,a new MQ radial basis function quasi-interpolation algorithm is proposed.Its construction and properties are presented,and it is used to approximate functions.The validity of the method is verified by the comparison between the numerical values and the true values of functions.The presented method is simple, easy to implement,accurate,and need not solve any linear equations.

MQ radial basis function;quasi-interpolation scheme;numerical approximation

1673- 9590(2017)05- 0118- 03

A

2016- 12- 06 基金项目:辽宁省博士科研启动基金资助项目

张继红(1979-)，女，副教授，博士，主要从事数值逼近及微分方程数值解方面的研究 E-mail:iamzjh@126.com.