电泳槽内水平段汽车白车身的气动力数值模拟

王东屏，陈济臣，赖宇阳，油忠超

(1.大连交通大学 机械工程学院，辽宁 大连 116028； 2.北京树优信息技术有限公司，北京 100062 )*

电泳槽内水平段汽车白车身的气动力数值模拟

王东屏1，陈济臣1，赖宇阳2，油忠超1

(1.大连交通大学 机械工程学院，辽宁 大连 116028； 2.北京树优信息技术有限公司，北京 100062 )*

针对白车身在电泳槽中运行过程的实际情况，建立了三维计算模型.基于日本CRADLE公司的SC/Tetra软件，利用八叉树方法对含有白车身的电泳槽模型进行了网格划分，应用k-ε标准湍流计算模型和SIMPLE算法对电泳槽中白车身外流场进行流场模拟分析.文中采用静网格模型和动网格模型两种不同方法对流场进行了模拟计算并对计算结果进行了对比.计算表明，两种方法所得结果相对误差小于4.96 %，说明计算结果可靠.计算得到汽车白车身在电泳槽水平运行时阻力值约为17.89 N，横向力值约为1.85 N，升力值约为522.36 N，计算结果为电泳生产线中遇到的脱钩、车身倾斜和车身颠覆等问题的解决提供了参考数据.

数值模拟;电泳槽;汽车白车身;气动力

0 引言

随着汽车工业的快速发展，我国汽车涂装技术水平有了十足的进步，许多涂装技术和工艺水平都达到了世界的前列[1].汽车白车身涂装中电泳过程占据着十分重要的位置，电泳是现在汽车涂装工艺中最主要的手段.在常见的汽车量产生产线中，通常需要冲压、焊装、涂装、总装这四大工艺[2].现代涂装工艺过程日益复杂，但无论如何复杂都可以把整个过程的工序分为前处理、涂装、烘干、面涂等工序[3].在这四道工序中涂装工序是重中之重.

国内外学者对汽车在电泳槽中运行的状况进行了模拟计算.高先海[4]运用商用软件Fluent对汽车驾驶室在电泳槽中运行的阻力进行了CFD模拟计算，获得汽车驾驶室在涂装电泳槽中运动过程获得的阻力，得出速度越大阻力越大，车身刚刚运动时所受阻力达到最大值.2014年肖宇[5]发明了一种新型的汽车仿真装置，该装置优化电泳部件，能够在实验室内模拟不同工艺条件下的电泳状态.FU Chang-Yong[6]研究了涂装电泳槽内空气污染、泡沫盒收缩的问题，对涂装电泳槽的各种环境都进行了研究.

涂装电泳槽的研究一直都是汽车流水线上重要的一部分，很多学者对汽车涂装电泳过程中出现的车身倾斜、车身颠覆和运动装置脱钩的问题进行了大量研究，但并没有针对这些问题得到可靠的理论数据.SC/Tetra是日本CRADLE软件公司于1998 年推出的CFD软件.该软件在汽车、电站、国防、旋转机械、环境等领域得到了广泛的应用[7- 8].

本文通过建立白车身模型和电泳槽模型，利用SC/Tetra软件对白车身在电泳槽中的运行进行了数值计算.采用静网格和动网格两种方法仿真模拟出白车身在电泳槽中运动时车身周围的压力变化、速度变化，得出在涂装工艺生产线中汽车白车身在电泳槽内水平运动阻力值、浮力值和横向力值，对已有电泳生产线中遇到的脱钩、车身倾斜、车身颠覆等问题的修正提供数据支持.

1 静网格数值计算模型

创建白车身电泳方案中车身水平段运动的分析模型，采用车静止，电泳液绕着车身运动的静网格模型.

1.1 汽车白车身模型

利用专业的建模软件Pro/E根据实际模型建立了汽车白车身3D模型，为了更好的体现汽车的平稳性同时也为了提高网格质量和运算速度，在保证计算准确的情况下省去了不必要的细小特征，其中汽车白车身长5.2 m，宽2.1 m，高1.36 m.

图1为电泳槽计算模型图.电泳槽长24 m，宽2 m，高4 m.车体距自由液面0.7 m，车身位于槽中间位置，槽中为电泳液.

图1 静网格计算模型

1.2 网格划分

网格的精细度对于模拟计算的精度有很大影响，网格划分得越多，流体运动轨迹越清晰.对于复杂计算域，根据计算域大小制定不同的网格划分方案[9].良好的网格质量对计算精度有非常重要的影响，为了更准确的模拟计算汽车白车身在电泳槽中运动所受的阻力、横向力和升力变化，对汽车白车身车体近壁层区域的网格进行细化.

如图2，采用四面体网格，车体表面划分两层边界层，网格从车体周围逐渐增大，远离车体的网格采用稀疏的网格，计算域中的整体网格数为1 010万.网格质量良好.

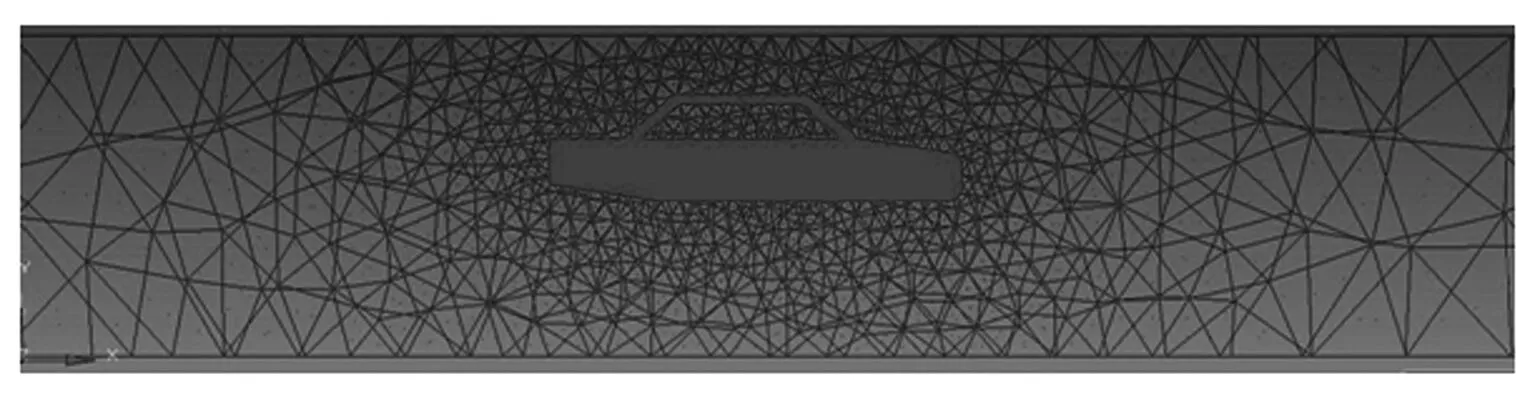
图2 计算模型网格

1.3 计算参数设定

计算模型参数设定中，车静止,电泳液以0.129 3 m/s的速度相对车体运动，电泳槽右侧设为速度入口，左侧设为压力出口.电泳槽底面采用移动壁面相对速度为0.129 3 m/s，顶部设为压力出口，其他壁面设为固定壁面.

设置工作环境：电泳液密度为1 030 kg/m3，温度为288 K，动力粘度为0.245 Pa·s，运用k-ε标准湍流计算模型和有限体积法对模型进行计算.

1.4 计算结果分析

图3为计算残差曲线，随着计算的进行曲线趋向于收敛.迭代3 000步，计算收敛，收敛精度为10-5.

图3 计算残差曲线图

如图4所示，在重力作用下，电泳槽内压力从上往下逐渐增大.车顶最大压力为7 205.10 N，车低压力为20 869.1 N，车头压力明显大于车尾部压力.

图4 车体纵向对称面压力分布图

如图5可以看出电泳液从车体周围流过并从车窗进入车体内部，并在车头和车尾部形成涡流，在车体头部和车窗顶部局部速度变大.

图5 速度矢量图

从表1可以看出采用静网格计算方法白车身在电泳槽中所受阻力、横向力和升力的大小.电泳液对车身的横向作用力基本对称，横向力很小.由于电泳液速度较低，车体的阻力较小.升力较大，车身产生的颠覆力矩就大，升力是影响车体颠覆和倾斜的主要原因.

表1 静网格下白车身受力值大小 N

2 动网格数值计算模型

动网格计算模型划分为A、B、C三个区域，区域B包含着车体以一定速度在电泳槽中匀速运动，A为拉伸区域，C为压缩区域.

2.1 汽车白车身模型

对白车身采用动网格模型进行模拟计算，B作为车身运动区域，A和C分别作为动网格计算模型的前后运动区域，汽车白车身长5.2 m，宽2.1 m，高1.36 m.

图6为电泳槽动网格计算模型图.车体位于电泳槽中，电泳槽长24 m，宽2 m，高4 m.车体距自由液面0.7 m，槽中为电泳液.

图6 动网格计算模型

2.2 网格划分

如图7，采用动网格，首先对车体周围小区域B进行网格划分，两层边界层，网格从车体周围逐渐增大.A和C区域是以B区域网格为基础进行拉伸的，其中A区域以0.98的缩小比例拉伸35层，C区域以1.02的伸长比例拉伸35层.

图7 计算模型网格

对车体近壁层区域依然采用四面体网格进行网格划分，计算域中的整体网格数为2 354万，网格质量良好.

2.3 计算参数设定

动网格模型，白车身周围区域B以0.129 3 m/s的速度向X正方向运动，车身定义为moving wall，车动引起车体周围电泳液的扰动.电泳槽的上表面作为压力出口，右侧设为压力入口，左侧作为压力出口.其他壁面设为固定壁面.

电泳液的参数设定及湍流模型的选取与静网格计算时一致.

2.4 计算结果分析

图8是汽车白车身运行到电泳槽中间位置时的压力分布图.能够看出电泳槽内压力主要分布规律是从上往下逐渐增大，其中车头压力明显大于车尾部压力.

图8 车体纵向对称面压力分布图

随着白车身在电泳液中的运动，车头处电泳液速度明显大于车尾处，车体内部电泳液的流动引起小范围的涡流.

表2可以看出，白车身在电泳槽中采用动网格的运动模型，分别产生阻力17.89 N、横向力1.85 N和升力522.36 N.

表2 动网格下白车身受力值大小 N

3 对比分析

文中运用不可压缩的力学模型，采用了静网格和动网格两种不同的计算模型对汽车白车身在电泳槽中运动情况进行了数值模拟计算.

图9显示了在静网格和动网格两种计算模型下车身表面压力分布图，两图车身压力都是从车顶向车身底部逐渐增大的趋势.

图9 汽车白车身两种模型下压力分布图

在两种计算方法下，分别取车顶、车底、车左侧和车右侧面的同一位置的压力值，如表3所示.

表3 两种模型在车表面同一位置压力值大小对比 Pa

对比表3可以看出，车顶、车底、车身左侧、车身右侧在同一位置的压力误差分别为1.54%、0.85%、0.57%和0.65%，各压力相对误差较小，两种方法所得白车身表面压力分布基本保持一致.

对比表4数值，可以获得汽车白车身在电泳槽中受到的各个方向作用力的大小.阻力值相对误差为3.76%.横向力相对误差为4.96%，升力值相对误差为0.41%，各气动力相对误差小于等于4.96%.两种方法计算结果基本一致.

表4 两种模型白车身受力值大小对比 N

4 结论

文中采用静网格模型和动网格模型两种数值计算方法分别对汽车白车身在电泳槽中运动进行了模拟计算，并对计算结果进行分析得出以下结论：

(1)采用静网格和动网格两种计算方法所得到的车身表面压力分布规律基本一致.汽车白车身在车顶、车底、车身左侧和右侧在同一位置压力的相对误差均不超过1.54%;

(2)采用静网格和动网格两种计算方法，得到汽车白车身的阻力、横向力和升力相对误差不超过4.96%.各方向作用力大小基本一致，计算数据具有较大可靠性;

(3)两种计算方法得到的升力分别为520.22 N和522.36 N，升力值较大，是影响车身脱钩、倾斜和颠覆的主要因素.

[1]邢永庆.轿车涂装线生产准备过程分析及改进[D].吉林:吉林大学,2012.

[2]孙玉兵,回金楷,韦兴民,等.浅谈车身试制涂装线的规划设计[J].现代涂料与涂装,2011(12):38- 40.

[3]董武波.涂装前处理过程中喷嘴的选择、排布及保养[J].汽车工艺与材料,2008(8):22- 24.

[4]高先海,张帅,张宗元,等.涂装电泳槽内汽车驾驶室的运行阻力数值模拟[J].汽车零部件,2012(9):77- 79.

[5]肖宇,荀华杰,徐中琼.汽车电泳仿真装置:中国,CN201410068417.1[P].2014- 09- 26.

[6]CHANG-YONG F U,CHENG W H,HAN H Q.Analysis of Electrophoresis of Car Body Surface Shrinkage Causes and Countermeasures[J].Modern Paint & Finishing,2012(5):3- 100.

[7]梅琼峰，于沪平，范秦寅.基于SC/Tetra模拟的搅拌机设计优化：A集[C].北京：中国CAE工程分析技术，1994.

[8]张罗莲.基于SC/Tetra重叠网格法的交叉旋转模型分析[J].计算机辅助工程,2012(4):69- 71.

[9]刘海锋.网格结构精细化有限元分析方法研究[D].浙江:浙江大学,2010.

Numerical Simulation of Aerodynamic Force of White Car Body Running in Horizontal Section of Electrophoresis Tank

WANG Dongping1，CHEN Jichen1，LAI Yuyang2，YOU Zhongchao1

(1.School of Mechanical Engineering,Dalian Jiaotong University,Dalian 116028,China; 2.Beijing SOYOTEC.Co.,Ltd，Beijing 100062,China)

According to the actual situation of the white car body running in the electrophoresis tank,a three dimensional calculation model was established. Based on SC/Tetra software of Japan CRADLE company,mesh of electrophoresis tank which contains the white car body was divided in using the octree method.The outflow field of the white car body running in the electrophoresis tank was analyzed byk-εstandard turbulent flow model and SIMPLE algorithm.Two methods of moving grid and static grid were used to simulate calculation,and results were compared in this article.The result show that the relative error of the results of the two methods is less than 4.96%,and the calculation results are reliable.The resistance value is about 18 N,the transverse force value is about 1.8 N,and the lift value is about 520 N for the white car body.

numerical simulation;electrophoresis tank;white car body;aerodynamic force

1673- 9590(2017)05- 0033- 04

A

2016- 10- 10

王东屏(1962-)，女，教授，博士，主要从事空气动力学相关研究 E-mail:wdp1962@163.com.