表贴式永磁同步电机铁耗计算仿真分析
2017-09-29马思群袁冰辛志峰孙彦彬
马思群,袁冰,辛志峰,孙彦彬
(1.大连交通大学 交通运输工程学院,辽宁 大连 116028; 2.天津电力机车有限公司,天津 300452)*收稿日期:2016-07-18基金项目:国家自然科学基金资助项目(51220001,51405057);中国铁路总公司科技研究开发计划资助项目(2013J012-B);辽宁省教育厅科学研究计划资助项目(L2014182)作者简介:马思群(1969-),男,教授,博士,主要从事复杂装备性能仿真E- mail:251437650@qq.com.
表贴式永磁同步电机铁耗计算仿真分析
马思群1,袁冰1,辛志峰2,孙彦彬1
(1.大连交通大学 交通运输工程学院,辽宁 大连 116028; 2.天津电力机车有限公司,天津 300452)*收稿日期:2016-07-18基金项目:国家自然科学基金资助项目(51220001,51405057);中国铁路总公司科技研究开发计划资助项目(2013J012-B);辽宁省教育厅科学研究计划资助项目(L2014182)作者简介:马思群(1969-),男,教授,博士,主要从事复杂装备性能仿真E- mail:251437650@qq.com.
基于FLUX对某型号表贴式永磁同步电机铁耗进行仿真分析研究,根据电机的传统铁耗Bertottti计算模型,得出电机不同磁密的定子铁心损耗;在考虑旋转磁场影响的条件下,首先利用有限元法改进计算模型,通过对定子铁心仿真分析,得到不同区域特征点磁场分布情况及磁密变化曲线;然后将径向和切向磁密分量叠加得到损耗,计算结果与传统模型进行对比,铁耗增加比例为19.325%,与最新研究文献的研究结果相符.
永磁同步电机;有限元法;铁心损耗;磁场分析
0 引言
永磁同步电机由于其高效率、启动转矩大、高速恒功率等一系列优点,已广泛运用于轨道交通车辆的牵引系统[1].定子铁心损耗为电机的主要损耗之一,铁损偏高会造成电机定子温度升高,尤其当应用于轨道交通车辆时,会严重影响其正常运行以及造成牵引系统效率低下等问题;正因如此,越来越多的学者开展电机铁耗研究.目前国内在研究电机铁耗时一般假设硅钢片内磁场分布均匀,通过正弦波电源下的B-P损耗曲线得出各损耗系数,利用经验公式近似计算铁耗[2].文献[3]指出电机在实际运行时,各区域磁密是分布不均的,比如影响电机铁耗最大的定子齿部、轭部的磁密大小在运行时是不同的,这就会导致局部磁滞损耗较大;而且,电机在运行时的磁矢量也是变化的,若采用分布均匀的磁场进行损耗计算,将产生较大的误差.
因此,如何获得准确的铁耗计算模型成为研究热点.目前,Bertotti铁耗分离模型是较为常用的计算模型[4];在此基础上,有学者通过研究非正弦谐波磁场来改进计算模型,该模型基于研究交变磁化得到磁滞损耗[5].而事实上永磁同步电机在运行时,由于三相绕组中的交变电流不完全等价,还会引起旋转磁场的产生.
本文通过对某型号表贴式永磁同步电机进行电磁仿真,重点分析在考虑旋转磁场作用时磁密不均匀对电机定子铁耗的影响机制,并在此基础上研究了电机不同区域磁密的波动轨迹,并与传统模型计算出的铁耗数据进行对比.
1 Bertotti铁耗分离模型
Bertotti铁耗分离模型是根据铁耗产生的机理将铁耗分为三部分,分别为磁滞损耗、涡流损耗和异常损耗[6],其表达式为:
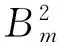
(1)
其中:P为铁耗(W/m3),kh为磁滞损耗系数,ke为异常损耗系数,f为磁场频率,Hz,σ为电导率,S/m,d为永磁体厚(m),Bm为磁密峰值,T.
由式(1)可知,铁耗求解的过程在于获得kh和ke.通常情况下根据硅钢片供应商提供的正弦波电源下的B-P损耗曲线,求得各项损耗系数,再根据经验公式来近似计算铁耗[2].表1是利用式(1)计算24槽8极表贴式永磁电机在B=1T、B=1.5T和B=2T时得出的各损耗分量值:

表1 Bertotti模型各损耗分量(f=50 Hz)
注:硅钢片为DW270-35的材料
该模型中的Bm为电机磁密峰值,而电机在实际运行时各区域的磁密、磁矢量是动态变化的;此外,通过一维正弦交变磁场得到的Bertotti铁耗计算公式与实际运行的二维非正弦旋转磁场有很大的不同,因此依据该模型进行计算误差较大,应将磁密分解成径向和切向分量叠加计算损耗[7].
2 基于有限元法的铁耗计算过程
定子铁耗当属电机损耗中较复杂且重要的,其加工工艺、硅钢片材料及磁场频率等都是影响定子铁耗的重要因素,正确计算铁耗的前提是建立合理的计算模型.基于FLUX的LS磁滞模型通过将有限元计算结果中每个单元的B(t)值按实测的材料特性重新构建H(t),并据此准确计算因材料磁滞效应而带来的损耗,因此该计算方法更加符合铁耗产生的基本机理.
2.1 模型的建立及参数设置
FLUX是一款针对电机、变压器等电磁设备的专业2D及3D电、磁、热分析软件,由全球领先的CAE软件制造商Magsoft研发,对产品进行电磁优化设计,具有可靠、易用、精确、高效的特点,能够提供精确仿真结果,降低产品成本,缩短研发周期.利用FLUX中Sketcher 2D模块建模.表2为该电机的基本参数.
喜爱他的外婆下达了两道命令:所有人洗澡都不许关门,必须满足孩子;在儿子观看某人洗澡的时候,其他人一律不准走动,集中在客厅看电视。于是,只要有人洗澡,儿子就有了看成人身体的机会,这样的情况持续了近两个月后,儿子对我们的洗澡完全失去了兴趣,不再坐在浴室门口看每一个人洗澡了,他的兴趣转移到了其他地方。

表2 电机模型基本参数
注:额定转速:750 r/m;额定转矩:2 N·m;绕组形式:3相星形绕组;永磁体材料:NdFeB(N35H).
在FLUX仿真中,为了减小模型节点数、提高运算效率,通常只需建立一部分模型,并通过设定边界条件及周期的方法模拟整体有限元模型的性能,如图1(a)所示;然后将电机模型不同区域进行分类附属性和材料,如图1(b)所示;根据电机

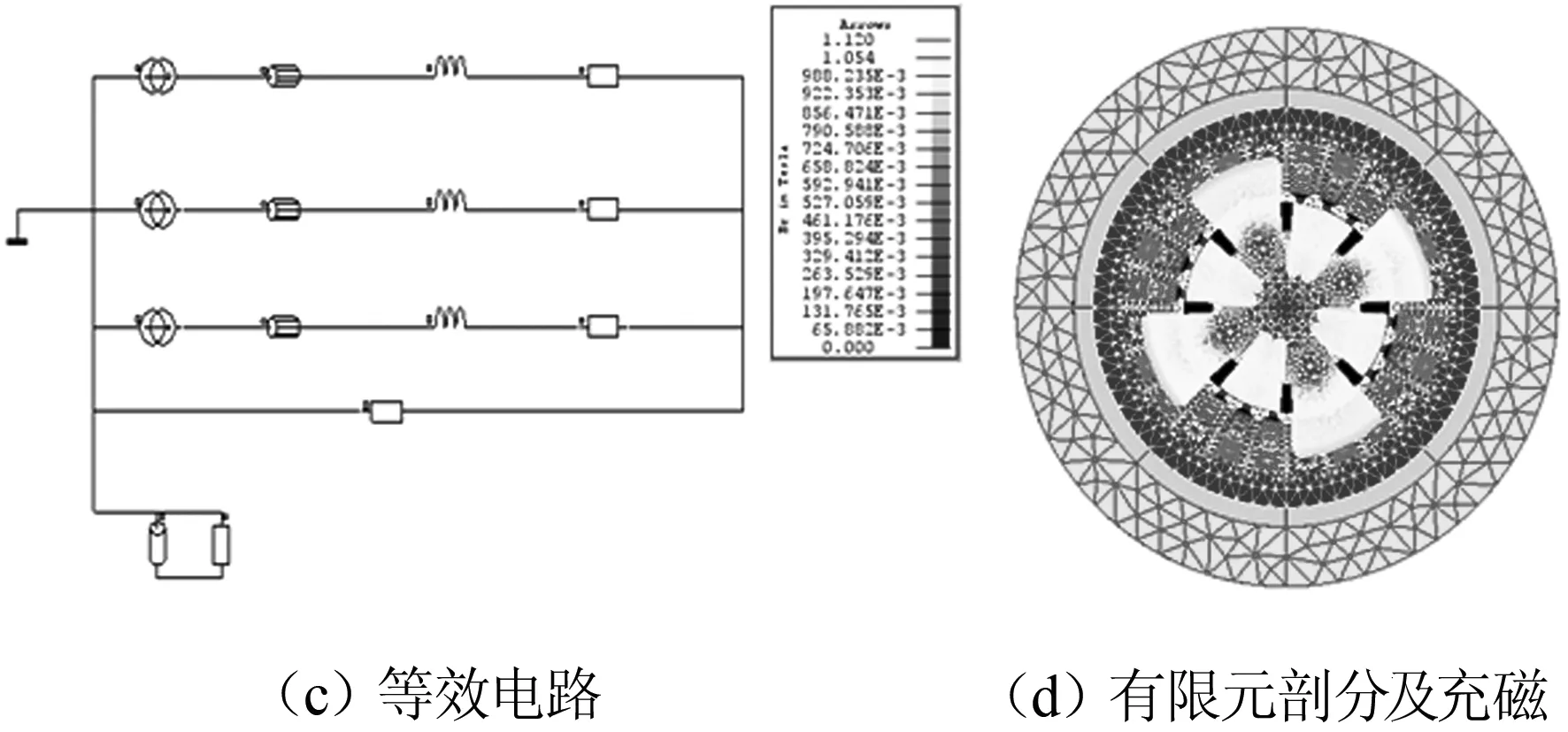
图1 模型的建立及参数设置
工作原理建立等效电路,如图1(c)所示,最后设置绕组和充磁,根据电流的方向设置充磁方向,并对设置完成的模型进行网格划分,有限元模型及充磁显示如图1(d)所示.
2.2 特征点选取
计算定子铁耗时需先对磁场进行仿真分析;定子铁心不同区域磁场分布不同,在获得整个定子铁耗时不可能将内部所有点进行计算.利用有限元基本思想可有效便捷的获得整个定子铁心的损耗,即:将定子铁心可近似为有限个相连的离散区域,选取每个不同区域内的特征点,依次对每个特征点进行磁场分析并求出铁耗,再将特征点所在区域的铁耗叠加[8].
将定子铁心主要分为齿部、轭部、靴部和槽部四个区域,各区域结构和位置的差异导致磁场分布的不同,分析各区域的磁场规律,需要选取各区域磁密的特征点,特征点位于定子关键部位和交界处.特征点分布如图2所示,a点为定子靴部中点;b点为定子绕组槽下靴部中点;c点为定子齿、轭部交界处;d点是定子齿部中点;e点是定子轭部中点[8].
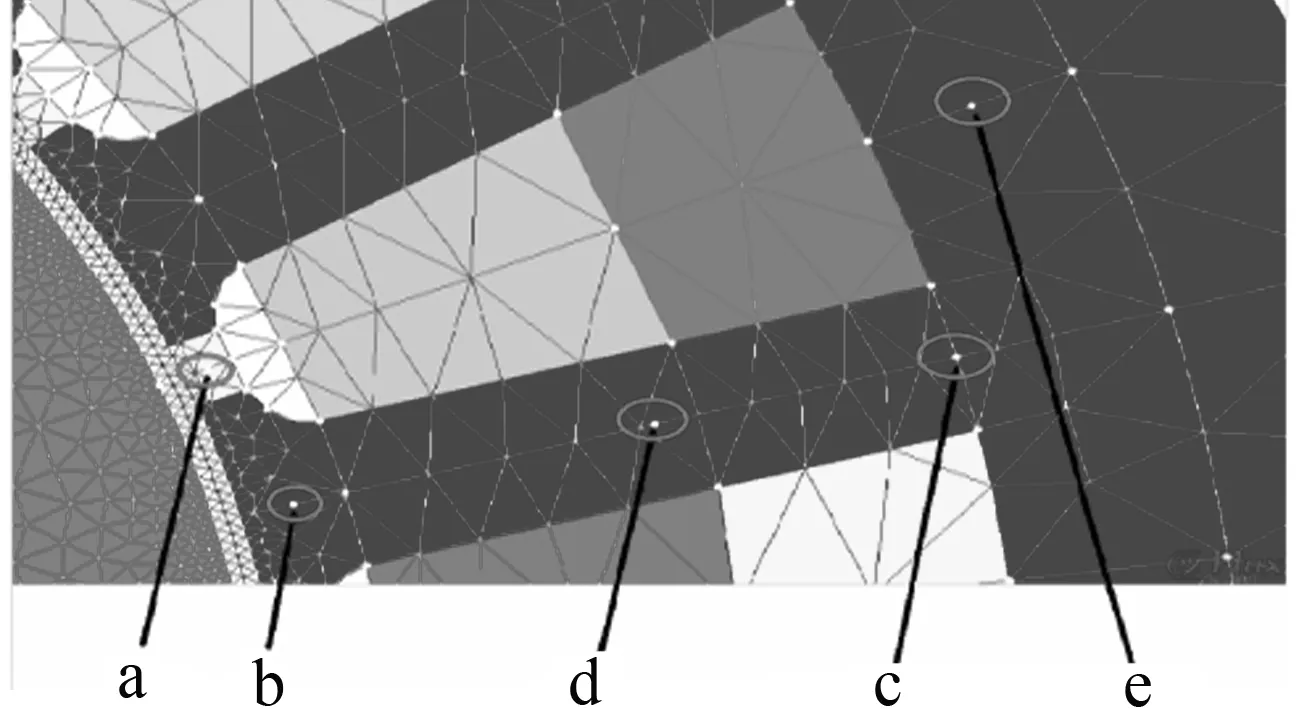
图2 定子铁心特征点分布
3 有限元仿真过程
3.1 磁场的分析
利用FLUX仿真软件对定子铁心的磁场进行仿真,得到特征点的磁密在两个周期内的变化曲线如图3所示.
通过对得到的磁密波形分析可知:b、d、e 三点所在区域磁密波动较大, a、 c 两点所在区域磁密波动相对较小.经仿真计算,该型号电机的提前角为7.5°,由于FLUX中是通过设置转子与d轴的夹角来确定电流提前角的,因此d轴所在位置滞后转子7.5°,所以除e点外,其它所有点均与-7.5°轴对称(而非0°轴),e点由于位于定子轭部中点,远离气隙,且受输入电流影响较小,因此关于0°轴对称 ;d点在定子齿部磁密幅值最大,为 1.617T;a 点由于靠近气隙,受到谐波的影响,磁密波形有一定变形;同时也证明了定子各区域的磁密幅值是动态变化的,较Bertotti模型,有限元法模型更为准确,符合电机实际运行的状态.

图3 特征点的磁密变化曲线
分析定子在工作时磁场分布情况,研究其产生磁密波动的原因,为铁耗的产生提供依据,通过对特征点磁密曲线峰值磁场分析,得出峰值磁密时定子磁场分布如图4所示.
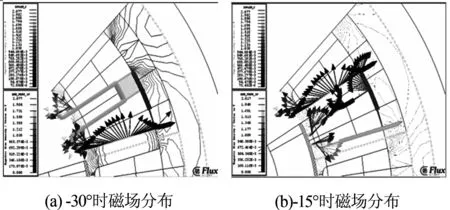
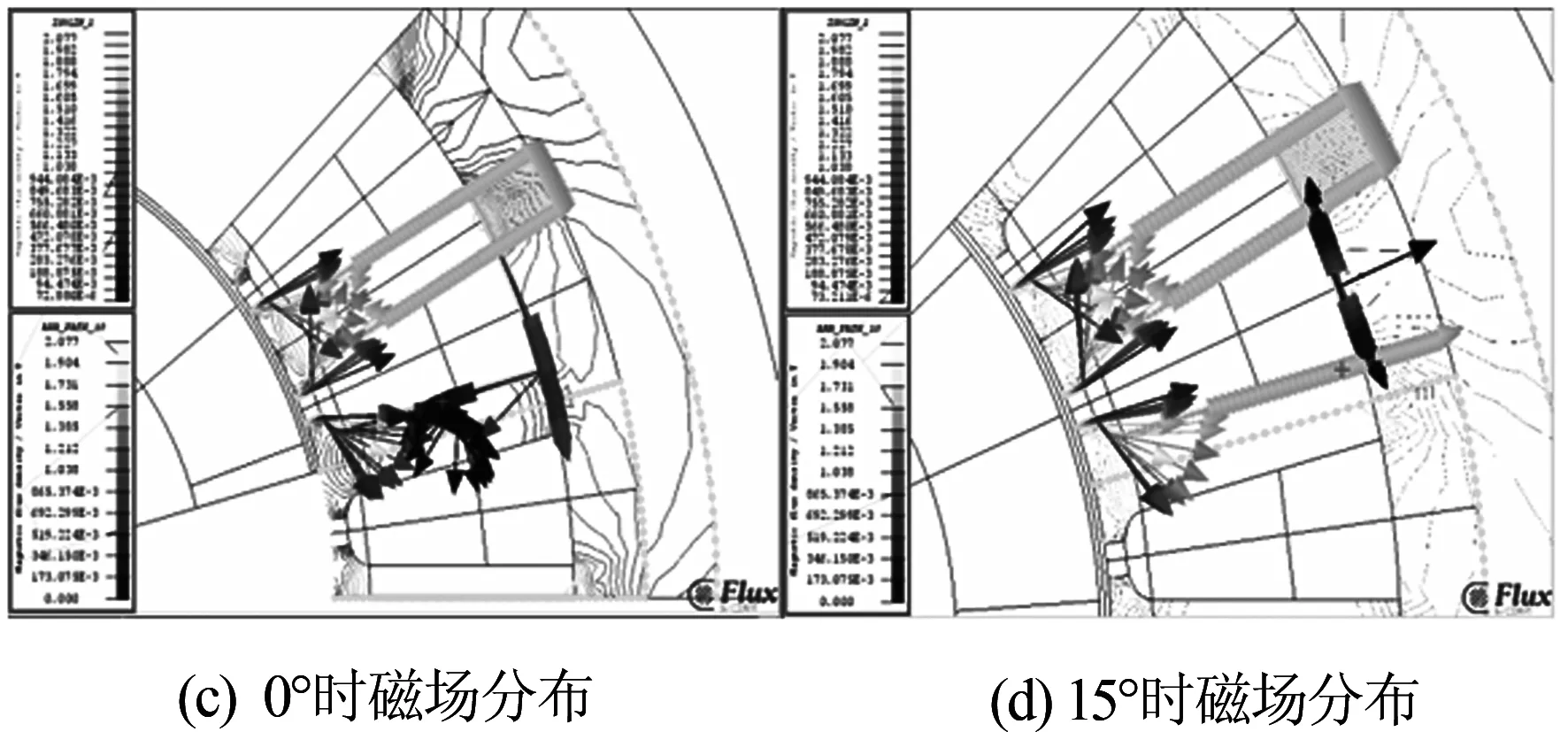

图4 峰值磁密时定子磁场分布
由计算结果可以发现,定子磁密波动受永磁体旋转影响,当转子转过角度为电流提前角的倍数时(电流提前角θ=7.5°),磁场线发生改变,此时磁密幅值将产生拐点,因此电机在转子转过两个周期(-π/4~ π/4)时,取±2θ、±4θ、0°和45°六个角度进行磁场分析,发现电机在转子转动-30°时(与-15°相同,方向相反),由于永磁体磁场方向的改变而在定子侧面产切向磁场,此时定子各区域的磁密值最小;-30°~-15°时,切向分量逐渐减小,定子各区域磁密将逐渐增大,当转子转至0°时(与45°相同,方向相反),磁场方向全部为径向方向,因此磁密达到最大值,以上分析均与图3各图相符合,验证了仿真的准确性.
3.2 铁耗的计算
由于电机运行时三相绕组中的交变电流不完全等价,不但会在定子铁心中感应出交变磁场,还会产生旋转磁场.为了使铁耗的计算更加准确,进一步分析旋转磁场对定子铁耗的影响,需要对特征点磁场进行分解,得到切向分量Bx和径向分量By[9],仿真结果如图5所示(图5中虚线表示By分量,实线表示Bx分量).
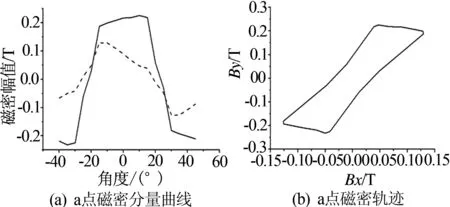
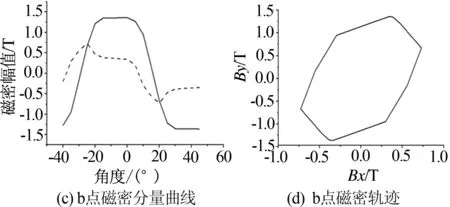

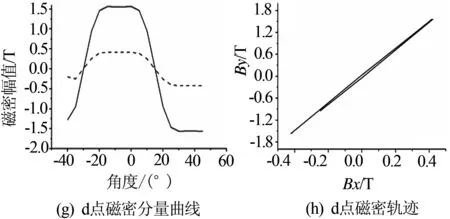
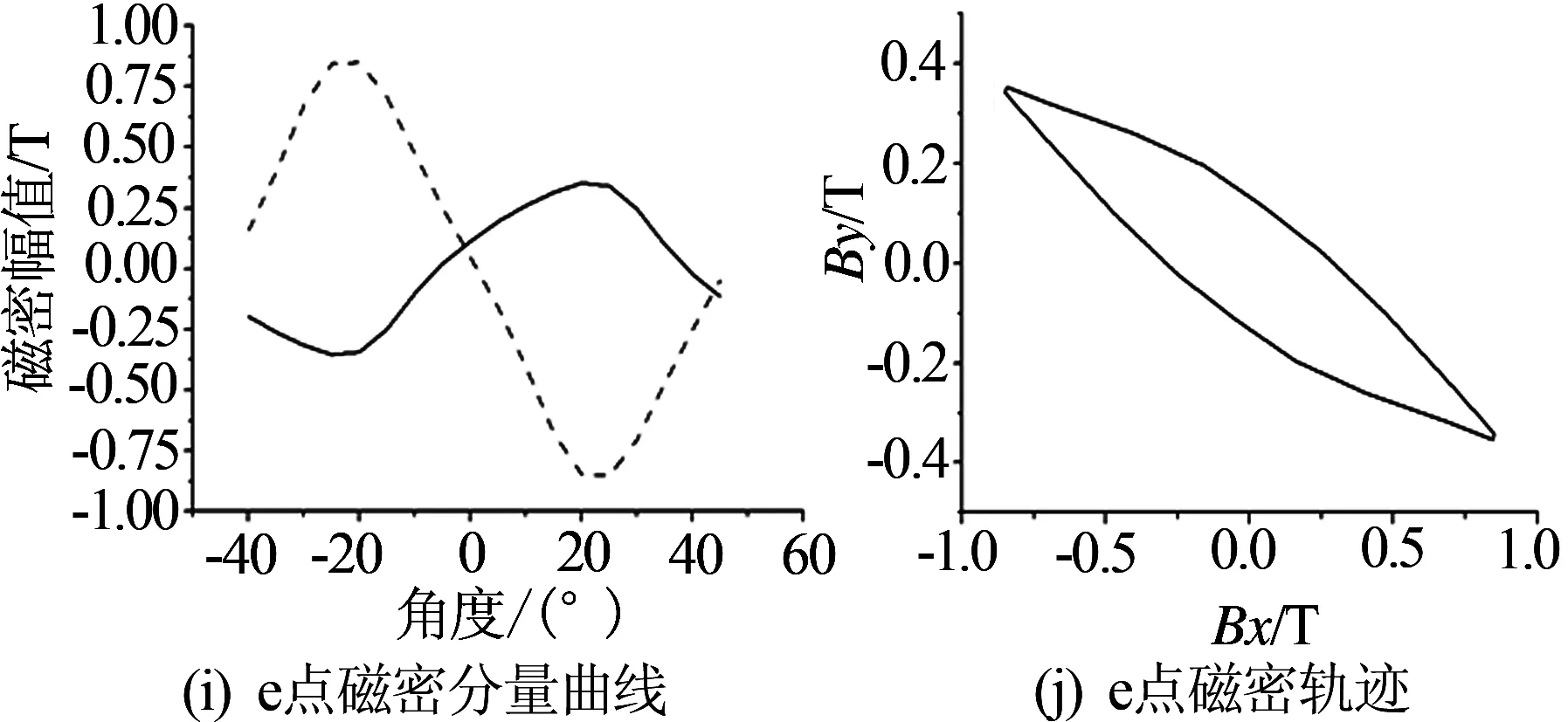
图5 特征点的磁密分量曲线及轨迹
由仿真结果可知,正常磁密轨迹矢量波形会呈现近似椭圆的形状.比如在定子齿部(特征点b、d),磁矢量的主方向是径向;在定子轭部(特征点e),其主方向是切向;在齿部、轭部交界处(特征点c),磁矢量包含径向、切向分量;其中b点受到旋转磁场作用最为强烈,其次是c点;而d点轨迹几乎为直线,变化较为规则,原因是定子齿部受交变电流产生的磁场的影响较大,且受气隙磁密影响较小.a、c和e点的磁密轨迹不规则,是由于受旋转磁场和交变磁场共同作用[10].a点位于定子靴部的中点,其轨迹近乎为平行四边形,是由于离气隙较近,受到气隙磁密波动的影响.
由于磁密的分量随着时间的变化而变化,因此铁耗计算公式如下:
(2)
式(2)中:Khi为第i个单元的磁滞损耗系数;Kci为第i个单元的涡流损耗系数;Kei为第i个单元的异常损耗系数;f为磁场频率;T为磁场周期;Bxi为第i个单元的切向分量;Byi为第i个单元的径向分量;提取特征点磁密的径向、切向分量幅值,带入式上式得到损耗分量值和定子总铁耗.
由表3得:与Bertotti模型结果相比,旋转磁场作用时定子铁耗值增大了1.1517 W,增加比例为19.325%.由此可见旋转磁场作用对铁耗的影响不可忽略;通过此方法同时可以看出各类损耗所占定子铁耗总量的比例,涡流损耗、磁滞损耗仍旧占据了铁耗的大部分.
4 结论
本文通过将有限元模型与Bertotti铁耗分离模型对比,采用有限元法将旋转磁场作用时的铁耗进行分析,得出以下结论:
(1)利用FLUX软件,直接可以得到结构中的任意一点的磁密,节省了仿真时间,提高了效率;
(2)将波动的磁密进行分解,求得各个区域的铁耗,将求得的铁耗进行叠加可以得出总的定子铁耗;
(3)引起磁密波动的原因是定子在工作时受旋转磁极的影响;
(4)定子铁心各区域的磁密分量并非标准的正弦波形;除定子齿部外其他区域磁密轨迹受旋转磁场的影响较大,不可忽略.
以上结论对于永磁电机的铁耗计算与磁场分析具有重要的参考价值;计算得到的数据可为电机效率和温升计算提供依据.
[1]徐强.永磁同步电机在轨道交通牵引系统中的应用及特点[J].科技信息,2013,(2):378-379.
[2]崔杨,胡虔生.硅钢片损耗的分析与计算[C].宁波:小功率电机学术交流会,2006.
[3]张涵,谢宝昌,张舟云,等.车用永磁同步电机铁耗的快速计算方法[J].电机与控制应用,2013 (12):9-14.
[4]张继鹏,苏锦智,付荣华,等.高速交流永磁发电机定子铁心损耗计算[J].微电机,2014 (11):10-14.
[5]BOGLIETTI A,CAVAGNINO A,IONELD M A. General Model to Predict the Iron Lossesin PWM Inverter-Fed Induction Motors[J].Industry Applicatios,IEEE Transactions on,2010,46(5):1882-90.
[6]刘光伟,赵新刚,张凤阁,等.高速永磁爪极电机铁耗与空气摩擦损耗计算[J].电工技术学报,2015,2:148-154.
[7]GUOQING Y,ZONGZE C,LIWEI S.Analysis of iron losses in induction motor with an improved iron-loss model[C].proceedings of the TransportationElectrificationAsia-Pacific (ITECAsia-Pacific), 2014 IEEE Conference and Expo.
[8]尹惠.永磁同步电机损耗计算及温度场分析[D].哈尔滨:哈尔滨工业大学,2015.
[9]左曙光 林福 吴旭东. 车用永磁同步电机转矩解析模型和波动特性分析[J].浙江大学学报(工学版),2015(9) :1731-1737.
[10]张洪亮. 永磁同步电机铁心损耗与暂态温度场研究[D]. 哈尔滨:哈尔滨工业大学,2010.
Calculation and Finite Element Analysis of Surface Mounted Permanent Magnet Synchronous Motor Iron Loss based on FLUX
MA Siqun1,YUAN Bing1,XIN Zhifeng2, SUN Yanbin1
(1.School of Traffic and Transportation Engineering, Dalian Jiaotong University, Dalian 116028,China; 2.Tianjin Electric Locomotive Co., Ltd,Tianjin 300452,China)
Iron loss simulation analysis of a type of surface mounted permanent magnet synchronous motor(PMSM)is conducted based on FLUX, and the motor stator core loss is calculated at different flux densities. According to the conventional model Bertottti, the calculation model is improved by finite element method under the condition of considering the influence of the rotating magnetic field, and magnetic field distribution and the flux density curve are obtained from feature point of different regional through the simulation analysis of the stator core.Then the radial and tangential magnetic dense components are added to obtain the loss. Compared with the traditional model, the iron loss ratio is 19.325%, which is consistent with the results of the latest research literature.
PMSM; finite element method; iron loss; magnetic field analysis
1673- 9590(2017)05- 0065- 05
A
