风力机柔性叶片翼型的气动特性研究

邓 勇 龚佳辉 何宇豪 陈 严 罗 振

1.国电南瑞科技股份有限公司，南京，2111062.汕头大学能源研究所，汕头，515063

风力机柔性叶片翼型的气动特性研究

邓 勇1,2龚佳辉2何宇豪2陈 严2罗 振1

1.国电南瑞科技股份有限公司，南京，2111062.汕头大学能源研究所，汕头，515063

基于柔性叶片大尺寸变形的特点，选取NPU翼型作为研究对象，采用Xfoil软件计算不同弦向变形时翼型的升阻力系数及俯仰力矩系数，并总结翼型变形后升力系数计算的修正公式。研究表明，柔性叶片弦向弯曲变形越大，翼型的升力系数越大，阻力系数也会有小幅度增大，但升阻比总体呈现增大趋势，有利于提升气动性能。翼型变形后的气动特性计算修正公式的计算结果与模拟仿真的结果也吻合较好。

柔性叶片；翼型；柔性变形；气动性能；修正公式

0 引言

翼型的研究主要包括翼型的分析和翼型的优化设计两方面，其中翼型的分析是研究翼型的参数对翼型的气动性能的影响。

目前，国内外关于翼型的研究主要包括翼型气动性能和翼型变形。李占科等[1]为了研究不同柔度的柔性翼气动特性及抗风性等性能，制作了9种具有不同柔度的柔性翼；HYEONU等[2]研究了叶片内部结构对翼型变形的影响，指出剪切变形是翼型变形的主要原因；MARTIN等[3]把翼型截面看成一个变截面悬臂梁，研究了翼型变形机理并总结出翼型变形的数学模型；EELCO等[4]研究了柔性翼型变形的趋势，发现随着厚度的增大，大部分柔性叶片翼型的变形呈线性增加，少部分呈现减少的趋势，他们对柔性翼型和刚性翼型进行了对比，发现柔性翼型可以延迟失速和扩大风机运行范围。本文基于柔性叶片大尺寸变形的特点，提出叶片柔性变形引起的翼型气动外形变化能提高翼型气动性能的假设，研究翼型弦向弯曲变形对翼型气动特性的影响以及计算公式的修正及其对气动阻尼的影响。

1 基础理论

1.1翼型升阻力特性

翼型气动力由来自上下表面压力差的升力源，以及来自流体黏性和翼型形状的阻力源共同决定。将该气动力分解为两个分力，其中一个分力与来流方向垂直，由库塔-儒可夫斯基定理可知，此分力即为翼型升力，使翼型向上运动；另一个分力与来流方向平行，起到阻碍来流前进的作用，即为翼型阻力[5]，如图1所示，F、FL、FD和M分别表示单位长度的气动力、升力、阻力和俯仰力矩。

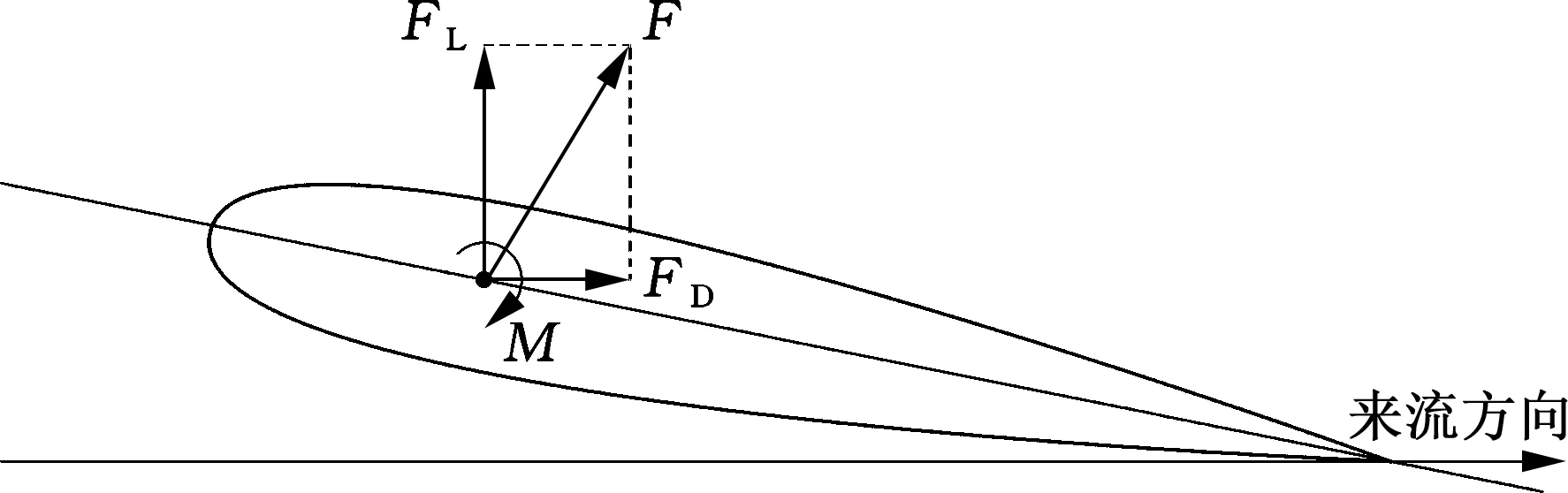
图1 翼型升力、阻力示意图Fig.1 The lift and drag of the airfoil

单位长度的翼型气动力可表示为

(1)

式中，CT为气动力系数；ρ∞为空气密度，U∞为来流风速；c为翼型弦长。

单位长度的翼型升力

(2)

式中，CL为升力系数。

单位长度的翼型阻力

(3)

式中，CD为阻力系数。

此外，对于翼型而言，还需要获取气动力对某一点(压力中心除外)的力矩，规定该力矩使翼型顺时针转动的方向为正方向。由于该力矩通常是指气动合力对于翼型前缘点的力矩，所以也称翼型俯仰力矩，可表示为

(4)

式中，CM为俯仰力矩系数。

由式(1)～式(3)可得

(5)

将式(2)～式(4)稍加变形，可得

(6)

作用在翼型上的升力、阻力和俯仰力矩很难通过理论计算求得，因此，在实际应用中经常通过实验手段获取某种翼型的升力系数CL、阻力系数CD和俯仰力矩系数CM，而此三个系数均为量纲一气动参数，一旦获取，即可方便地结合来流风速和实际需求的弦长求得对应翼型的升力、阻力和俯仰力矩。

对于特定的来流条件下的特定翼型，其升力系数CL、阻力系数CD和俯仰力矩系数CM主要与翼型攻角α有关，如图2所示。

(a)非对称翼型

(b)对称翼型图2 翼型升阻特性曲线示意图Fig.2 Lift-drag characteristic curve of airfoil

升力系数定义如下：

(7)

式中，A为物体平面面积。

对于长形物体(如飞机机翼或风力机叶片)来说，在定义中采用单位翼展的升力，于是平面面积被弦长所替代，则式(7)变为

(8)

在实际应用中，

CL=a0sinα

(9)

其中，a0为升力曲线斜率dCL/dα，而不是2π。值得注意的是，式(9)所示的简单关系仅仅适用于失速前区域，也就是附着流区域[6]。由于攻角较小(α<16°)，式(9)常常写成如下形式：

CL=a0α

(10)

式(10)适用于对称翼型。根据图2可知，对称翼型的零升力攻角α0=0°，非对称翼型在α0=0°时，升力系数大于零。因此，对于非对称翼型，对式(10)加以修正，使其适用于附着流区的升力系数的计算。

阻力系数CD在低攻角下几乎是恒量。在失速区，Viterna等于1981年提出了一种升阻力系数计算方法[7]，此方法在假设转子扭转角为零的情况下适用：在攻角α0=90°时阻力系数最大，即

CDmin=1.11+0.018δAR

(11)

式中，δAR为翼型的展弦比。

失速区阻力系数为

CD=B1sin2α+B2cosα

(12)

B1=CDmaxB2=(1/cosαs)(CDs-CDmaxsin2αs)

失速区升力系数为

CL=A1sin2α+A2(cos2α/sinα)

(13)

A1=B1/2

A2=(CLs-CD,maxsinαscosαs)·(sinαs/cos2αs)

式中，αs为开始失速的攻角，本文中开始失速的攻角为8°，所计算的攻角范围为8°≤α≤90°；CDs为对应开始失速攻角的阻力系数；CLs为对应开始失速攻角的升力系数。

1.2翼型变形

在航空航天领域，针对叶片变形所产生的非定常气动载荷控制技术，采用了智能叶片技术，即通过调整翼型几何形状，使叶片的几何物理属性均发生变化，达到改变翼面非定常流场结构、优化翼型气动特性的目的。

目前，用于翼型流场主动控制的智能结构一般是将传感器、作动器嵌入翼段主体结构之内，而将微控制器、信号处理以及功放等置于翼段主机结构之外，通过通信和控制网络连接，形成闭环系统，使结构能够感知翼面流场环境变化，并能针对这种变化作出适当反应，如图3所示[8]。

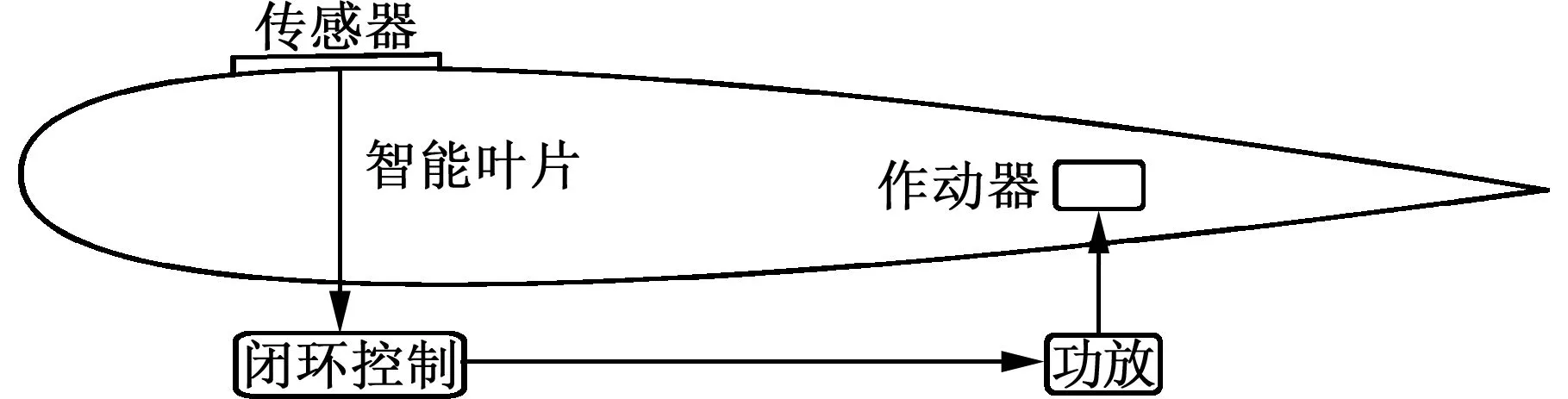
图3 智能叶片结构控制示意图Fig.3 The intelligent blade structure control

在风力机领域，目前考虑叶片变形情况的基本设计思路是：整个叶片的升阻力和力矩是基于微元段翼型的气动特性计算的，而将叶片变形引起的非定常气动效应转化为固定结构翼型的攻角变化。但风力机实际运行时，由于叶片的大型化、湍流风载及其瞬态效应，即使是在工作风速范围内，亦不可避免地使翼型自身结构产生较大变形[9]，因此，如需进一步提高风力机气动性能、运行安全性、瞬态风载反应能力和抗极端载荷能力，就必须充分考虑由于翼型结构改变而产生的气动特性变化。

目前通过改变翼型结构的有刚性襟翼和柔性襟翼[5]。刚性襟翼在实际运行时，主体段位置固定，而尾缘段则以铰接点为中心做不同角度的摆动。尾缘段摆动角度的不同，使得整体形状发生改变，从而引起翼型气动特性变化。尾缘段位置变化而形状固定，称为刚性襟翼。尾缘段的位置与形状均发生了改变，则称为柔性襟翼，柔性襟翼如图4所示。

图4 叶片翼型尾缘柔性襟翼Fig.4 The flexible flaps of blade airfoil trailing edge

为了充分利用风力资源和降低风电成本，单机大型化是现代风电机组发展的必然方向。单机大型化中的大尺寸叶片和高塔架的柔性不可忽略。根据柔性叶片大尺度变形的特点，风载荷会使柔性叶片向顺风向偏移，风力机的叶片柔性变形会导致翼型气动外形变化。本文提出柔性叶片弦向弯曲变形假设(即叶片柔性变形引起翼型气动外形变化而发生弦向弯曲变形，叶片柔性变形引起的翼型气动外形变化能提高翼型气动性能)以研究叶片柔性变形引起的翼型气动外形变化对翼型气动性能的影响，为大型风力机柔性叶片气弹分析提供参考。本文主要研究NPU翼型弦向弯曲变形对翼型气动性能的影响。

图5 NPU-WA-180翼型及弦向弯曲变形翼型Fig.5 The shape of deformed and undeformed NPU-WA-180 airfoils

2 翼型弦向弯曲的气动特性计算结果与分析

采用Xfoil软件(Xfoil6.99版本)对NPU-WA翼型进行数值模拟，雷诺数Re=1×106，马赫数为0。四种翼型及其弦向弯曲变形翼型气动特性如图6～图9所示。

(a)升力系数

(b)阻力系数

(c)升阻比

(d)俯仰力矩系数图6 NPU-WA-150翼型不同变形幅度下气动特性与原翼型对比Fig.6 Comparison between aerodynamic performance under different deformation scope and the original NPU-WA-150 airfoil

(a)升力系数

(b)阻力系数

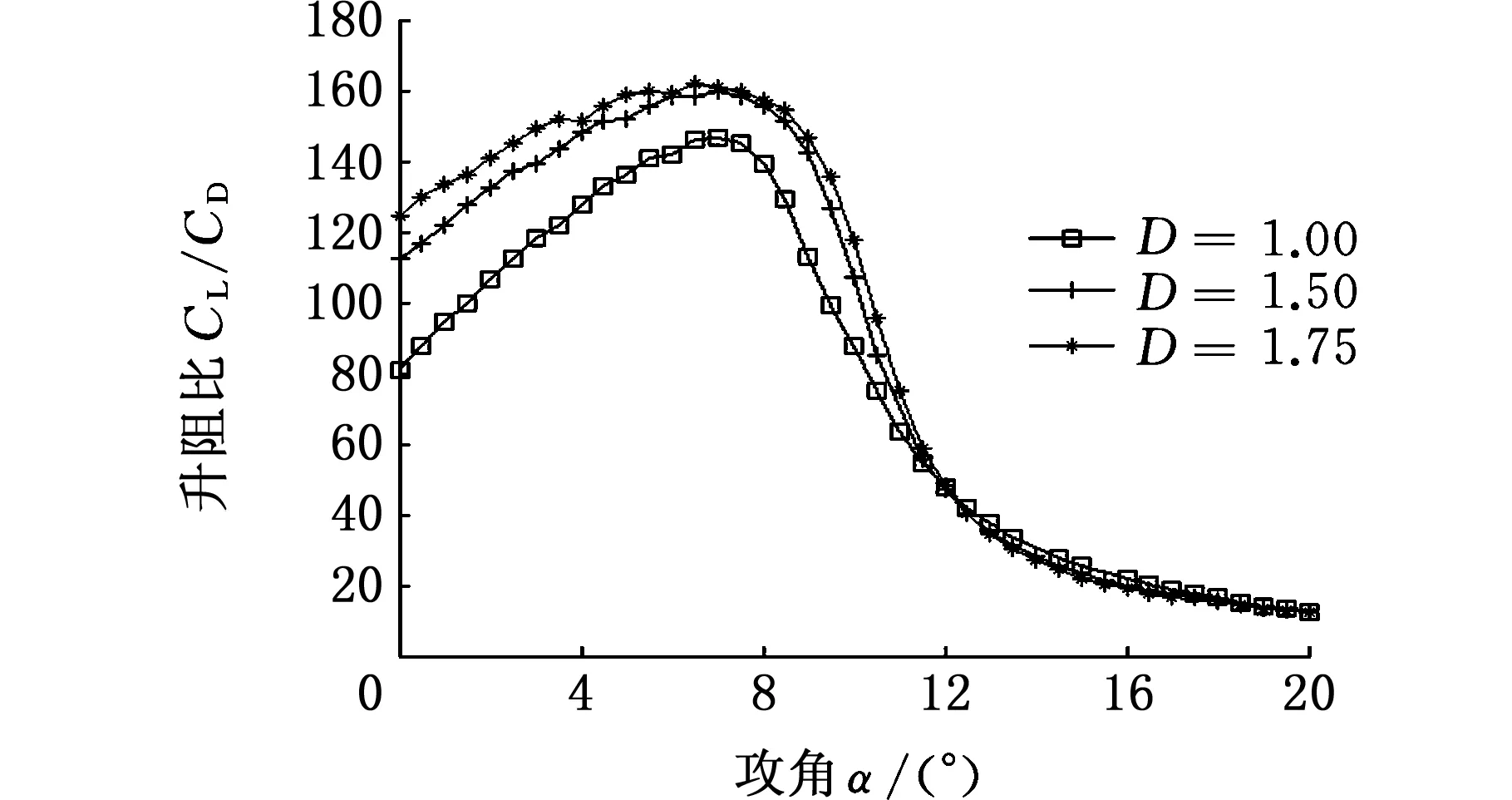
(c)升阻比

(d)俯仰力矩系数图7 NPU-WA-180翼型不同变形幅度下气动特性与原翼型对比Fig.7 Comparison between aerodynamic performance under different deformation scope and the original NPU-WA-180 airfoil

(a)升力系数

(b)阻力系数

(c)升阻比

(d)俯仰力矩系数图8 NPU-WA-210翼型不同变形幅度下气动特性与原翼型对比Fig.8 Comparison between aerodynamic performance under different deformation scope and the original NPU-WA-210 airfoil

(a)升力系数

(b)阻力系数

(c)升阻比

(d)俯仰力矩系数图9 NPU-WA-250翼型不同变形幅度下气动特性与原翼型对比Fig.9 Comparison between aerodynamic performanceunder different deformation scope and the original NPU-WA-250 airfoil

如图6～图9所示，由NPU-WA-150、NPU-WA-180、NPU-WA-210、NPU-WA-250不同变形幅度下气动特性与原翼型对比图得出：

(1)中弧线弯度增大的NPU-WA翼型升力系数CL总体上大于原NPU-WA翼型升力系数CL。翼型阻力系数CD总体变化较小，NPU-WA-210和NPU-WA-250翼型阻力系数CD基本保持不变。

(2)所计算的攻角0°～20°中，在0°～8°攻角区间为线性区域(翼型表面为完全附着流)，翼型升力系数CL随着攻角α增大保持增大趋势。在攻角8°～20°攻角区间为非线性区域(翼型表面为转捩流动或部分分离流动)，随着攻角的增大，升力系数CL先增大后减小。

(3)中弧线弯度增大后的NPU-WA翼型运行于0°～8°攻角范围时，其升力系数CL变化范围可完全满足同样计算攻角下NPU-WA原翼型的升力系数CL变化范围，且在整个区间内与攻角均保持线性关系，保证了计算结果的可靠性。

(4)中弧线弯度增大后的NPU-WA翼型运行于8°～20°攻角范围时，虽处于非线性区域，但其升力系数CL比原翼型亦有增大的趋势，有提升叶片气动性能的趋势。

(5)从升阻比曲线上来看，原NPU-WA翼型最大升阻比对应于α=8°，中弧线弯度变形倍数D=1.50时翼型最大升阻比对应于α=8°，而D=1.75的最大升阻比对应于α=6°；当α<8°时，D=1.75翼型的升阻比大于D1.50翼型的升阻比，变形后的翼型升阻比都比原翼型升阻比大，但NPU-WA-250有点差别，当6°<α<8°时，D=1.75翼型的升阻比小于D=150翼型的升阻比；当α<6°时，D=1.75翼型的升阻比大于D=1.50翼型的升阻比；当α>8°时，变形后的翼型与原翼型的升阻比基本相等。

(6)俯仰力矩系数CM随着中弧线弯度的增大而减小，有利于攻角变小时的变桨。

3 翼型变形的气动特性修正

根据NPU-WA翼型的中弧线弯度不同幅度的变形后数值模拟的结果，在低攻角0°～8°区域即附着流区，翼型的升阻比基本呈线性变化，在攻角大于8°的分离流区域，翼型的气动特性变化的不规律性和复杂度增加，式(10)的适用性受到限制，本文只是针对低攻角0°～8°区域的升力系数在不同变形幅度下进行计算，因此假设变形后翼型升力系数计算式为

CL=a0α+DCLα0

(14)

式中，D为翼型中弧线弯度变化的倍数;CLα0为原翼型在0°攻角下的升力系数。

选取NPU-WA-150和NPU-WA-250两种翼型，对其原翼型仿真得到的升力系数进行曲线拟合，结果如图10所示。

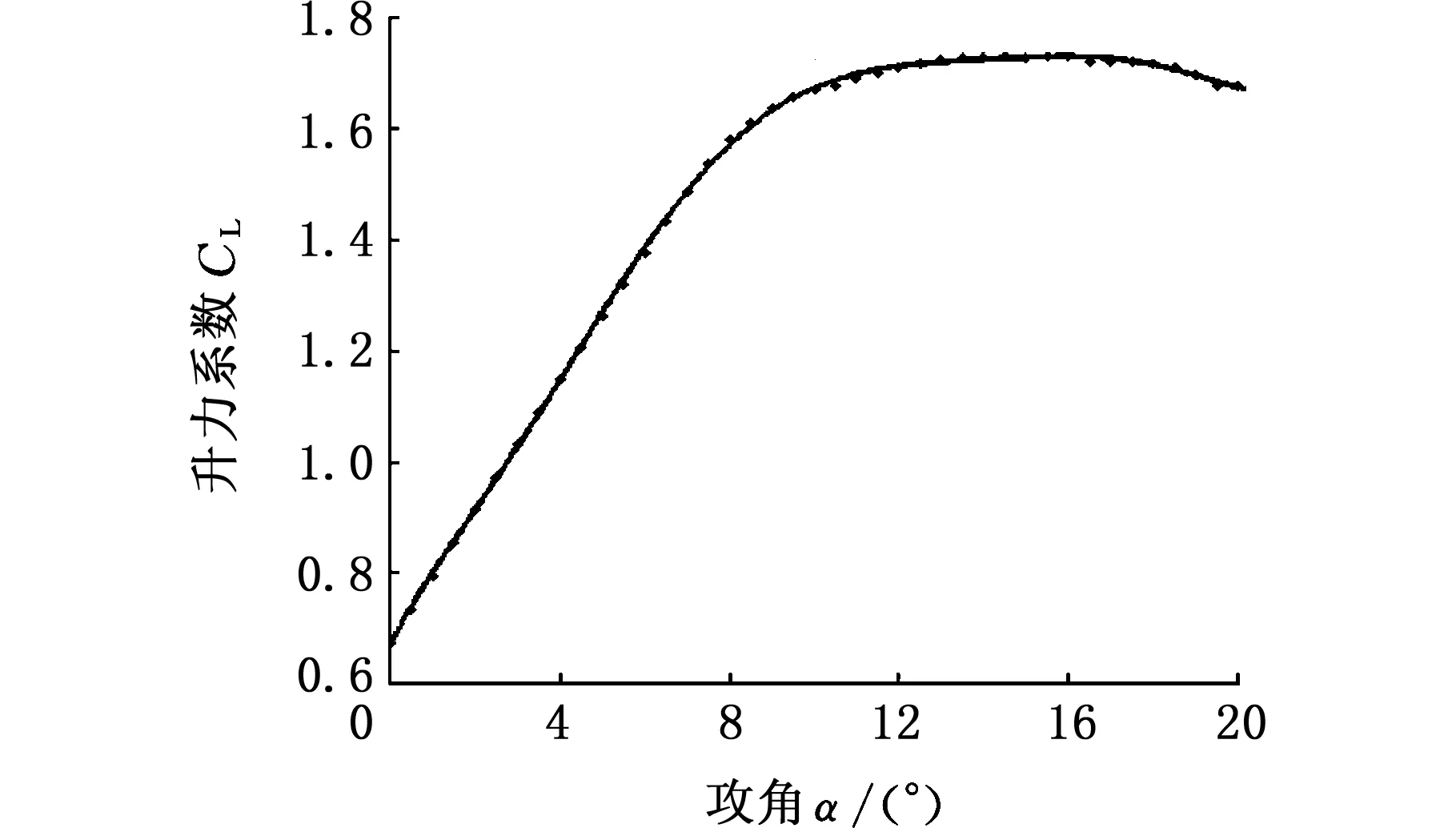
(a)NPU-WA-150翼型

(b)NPU-WA-250翼型图10 升力系数拟合曲线Fig.10 The lift coefficient curve fitting

将修正后的升力系数计算公式(式(14))求得的0°～8°攻角范围时的升力系数与仿真得到的结果进行比较，如图11所示，可以看出，根据升力系数在附着流区域的特点，本文所提出的翼型变形后升力系数计算修正公式所计算的结果与仿真结果吻合较好，相对误差保持在3%以内，因此，式(14)可以用于计算附着流区域即低攻角下的翼型中弧线弯曲变形后的升力系数。

(a)NPU-WA-150

(b)NPU-WA-250图11 升力系数计算与仿真结果比较Fig.11 Comparison between calculated and simulation results of the lift coefficient

4 结论

(1)采用Xfoil软件中弧线弯度变形倍数分别为1.50和1.75的两种不同变形幅度的NPU-WA翼型进行数值模拟，得知翼型在一定程度的弦向弯曲变形(即增大中弧线弯度)下可改善翼型的气动特性：①中弧线弯度增大后的NPU-WA翼型运行于0°～8°攻角范围时，其升力系数CL变化范围可完全满足同样攻角下NPU-WA原翼型的升力系数CL的变化范围，且在整个区间内与攻角均保持线性关系。②中弧线弯度增大后的NPU-WA翼型运行在8°～20°攻角范围时，虽处于非线性区域，但其升力系CL比原翼型亦有增大的趋势。③随着中弧线弯度的增大，在0°～8°攻角范围内时，翼型的升阻比逐渐增大，叶片气动性能明显提高，在8°～20°攻角范围内时，升阻比基本不变，整体上提升了叶片的气动性能。

(2)根据升力系数在附着流区域的特点，提出翼型中弧线弯度变化后的升力系数计算公式的修正公式，其计算结果与仿真结果吻合良好。

[1] 李占科, 徐顶国, 牛文. 不同柔度的柔性翼气动特性试验[J]. 航空动力学报,2011,26(1):136-140. LI Zhanke, XU Dingguo, NIU Wen. Aerodynamic Characteristics Test of Flexible Wings with Different Flexibility[J]. Journal of Aeronautical dynamics, 2011,26(1):136-140.

[2] HAO H, JU J, KIM D M. Compliant Cellular Structures: Application to a Passive Morphing Airfoil[J].Composite Structures,2013,106:560-569.

[3] PUTERBAUGH M, BEYENE A. Parametric Dependence of a Morphing Wind Turbine Blade on Material Elasticity [J]. Energy,2011,36:466-474.

[4] HOOGEDOORN E, JACOBS G B, BEYENE A. Aero-elastic Behavior of a Flexible Blade for Wind Turbine Application: a 2D Computational Study [J]. Energy ,2010, 35:778-785.

[5] 李春,叶舟,高伟,等. 现代大型风力机设计原理[M]. 上海：上海科学技术出版社, 2013. LI Chun , YE Zhou, GAO Wei, et al. Design Principle of Modern Large Scale Wind Turbine[M]. Shanghai: Shanghai Science and Technology Press, 2013.

[6] BURTON T, JENKINS N, SHARPE D, et al.风能技术[M].2版.武鑫译. 北京：科学出版社,2014. Wind Energy Techndogy[M]. 2nd Ed. Wu Xin Trans. Beijing: Science Press, 2014.

[7] RASMUSSEN F, PETERSEN J, MADSEN H. Dynamic Stall and Aerodynamic Damping[J]. Journal of Solar Energy Engineering, 1998, 121(3):150-155.

[8] 催尔杰,白鹏,杨基明. 智能变形飞行器的发展道路[J]. 航空制造技术,2007(8):38-41. CUI Erjie, BAI Peng, YANG Jiming. The Development Path of Intelligent Morphing Aircraft[J]. Aeronautical Manufacturing Technology,2007(8):38-41.

[9] BARLAS T K, VAN KUIK G A M. Review of State of the Art in Smart Rotor Control Research for Wind Turbines[J]. Progress in Aerospace Sciences, 2010, 46(1):1-27.

(编辑郭伟)

StudyonAerodynamicCharacteristicsofFlexibleBladeAirfoilsofWindTurbines

DENG Yong1,2GONG Jiahui2HE Yuhao2CHEN Yan2LUO Zhen1
1.Nari Technology Development Co.,Ltd.,Nanjing，211106 2.Institute of Energy Science,Shantou University,Shantou，Guangdong,515063

The deformation characteristics of flexible blade sizes NPU airfoil was selected as the research object, lift and drag coefficient and pitching moment coefficient calculation of different airfoil deformations to the string were carried out by using the Xfoil software and the correction formula of lift coefficient of airfoil calculation after deformation was summarized. The results show that the greater the chord bending deformations of the flexible blades, the greater the lift coefficients of the airfoils and the drag coefficients will increase slightly, but the lift drag ratio shows an overall increasing trend, which is beneficial to enhance the aerodynamic performance. The modified formula of aerodynamic characteristics after airfoil deformations is also in good agreement with the simulation results.

flexible blade； airfoil； flexible deformation； aerodynamic performance； correction formula

2017-02-20

国家电网公司科技项目(4500657183)；广东省应用型科技研发专项(2015B020240003)

TK8

10.3969/j.issn.1004-132X.2017.18.011

邓勇，男，1985年生。国电南瑞科技股份有限公司电气控制分公司研究人员，汕头大学能源研究所助理研究员。研究方向为可再生能源技术。发表论文4篇，获中国专利8项。E-mail：dengyong@stu.edu.cn。龚佳辉，男，1987年生。汕头大学能源研究所硕士研究生。何宇豪，男，1991年生。汕头大学能源研究所硕士研究生。陈严(通信作者)，男，1964年生。汕头大学能源研究所教授、博士研究生导师。E-mail：ychen@stu.edu.cn。罗振，男，1985年生。国电南瑞科技股份有限公司电气控制分公司风电研发工程师。