基于虚设运动副的并联机器人静态误差建模与标定

赵延治 宋晓鑫 杨建涛 齐立哲 何 勇 赵铁石

1.燕山大学河北省并联机器人与机电系统实验室，秦皇岛，0660042.先进锻压成形技术与科学教育部重点实验室(燕山大学)，秦皇岛，0660043.天津智通机器人系统有限公司，天津，3017004.中国科学院深圳先进技术研究院，深圳，518055

基于虚设运动副的并联机器人静态误差建模与标定

赵延治1,2宋晓鑫1,2杨建涛1,2齐立哲3何 勇1,4赵铁石1,2

1.燕山大学河北省并联机器人与机电系统实验室，秦皇岛，0660042.先进锻压成形技术与科学教育部重点实验室(燕山大学)，秦皇岛，0660043.天津智通机器人系统有限公司，天津，3017004.中国科学院深圳先进技术研究院，深圳，518055

基于并联机器人影响系数和虚位移原理，以一般空间并联机器人为例，通过虚设运动副，提出一种并联机器人静态误差建模与分析的通用新方法。该方法用于确定各个原始加工装配误差源对并联机器人末端位姿的独立影响，具有物理意义明确、建模分析便捷等优势。在此基础上，基于虚设运动副建立了3-P(4S)并联机器人各误差映射矩阵，并对该机器人开展了静态误差标定实验研究。实验结果表明，基于该方法标定后，3-P(4S)并联机器人输出定位误差最大值由0.585 mm减小到0.142 mm，标定后机器人定位精度明显提高，从而验证了该方法的有效性。

并联机器人；静态误差建模；虚设运动副；误差映射矩阵

0 引言

和串联机器人相比，并联机器人无误差累积，但由于其误差源较多，实际输出位姿与理想输出位姿依然存在着偏差。许多学者从不同角度提出了并联机器人静态误差分析的方法[1]。并联机器人静态误差建模的一般方法有D-H参数法[2-5]、环路增量法[6-7]、空间矢量法[8-13]、正交设计法[1,14]和摄动法[15-16]等。文献[2-5]用D-H参数法及由此形成的影响系数法和显著性分析方法对并联机器人进行误差分析，使得各原始误差参数形成的位姿误差矩阵具有简单而统一的形式；文献[6-7]结合球面并联机器人特点,采用环路增量法,建立球面并联机器人误差模型；文献[8-13]运用空间矢量法对并联机器人进行建模，得到并联机器人广义几何误差模型；使用正交设计法对并联机器人误差进行分析，定量分析了各误差源对机构输出误差的影响；文献[15-16]运用摄动法对并联机器人进行误差建模，明确了各误差源对末端位姿的影响。虽然上述理论与方法解决了一般并联机器人机构误差建模的问题，但均是统一考虑所有误差项建模，通过分离和辨识进行误差分析，建模过程较为复杂，且在具体分析某特定误差源对其机器人输出位姿的影响时，对应的误差建模求解与分析过程不够简明与便捷。本文基于并联机器人影响系数和虚位移原理，提出一种基于虚设运动副的并联机器人静态误差建模与标定通用新方法，该方法物理意义明确，建模分析便捷。使用该方法建模在设计之初就可以确定各个原始误差源对末端位姿的独立影响，从而可以有针对性地提高误差敏感构件的制造或者装配精度，进而有效提高机器人输出定位精度，具有较强的可操作性及实用性。

1 并联机器人静态误差建模的虚设运动副法

1.1基于虚设运动副的静态误差建模

若并联机器人的各原始误差源间相互独立，则各原始误差源引起的机器人末端输出的总位姿误差等于各原始误差源引起的局部位姿误差之和，即并联机器人误差的独立作用原理。本文提出的虚设运动副法就是在分别考虑各静态误差独立影响作用下，基于影响系数和虚位移原理进行的。图1为基于虚设运动副的误差建模流程图，在考虑各原始误差源时，首先刚化机器人原驱动，结合待分析误差源，在原有机器人机构基础上，通过添加相应虚拟运动副得到新的等效机器人机构，然后选取添加的运动副作为等效机器人机构的主动输入，基于影响系数，求解得到对应于该原始误差源与机器人输出位姿误差的误差映射关系，获得该误差所对应的误差映射矩阵。

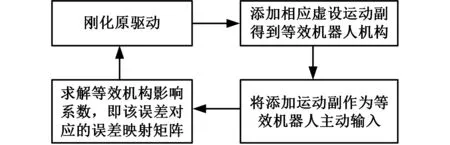
图1 基于虚设运动副的误差建模流程图Fig.1 Error modelling flow diagram based on VJP

为建立一般并联机器人误差建模的通用模型，从一般空间并联机器人机构出发，如图2所示，设其驱动由m个运动副p=(p1,p2,…,pm)T提供，其中包括主动转动关节和主动移动关节。由于制造和装配误差，各驱动副的实际转角或位移会在理论值pi(i=1,2,…,m)上产生Δpi的偏差量，根据误差独立作用原理，在考虑Δpi引起输出构件的位姿误差时，不考虑其他构件误差的影响。

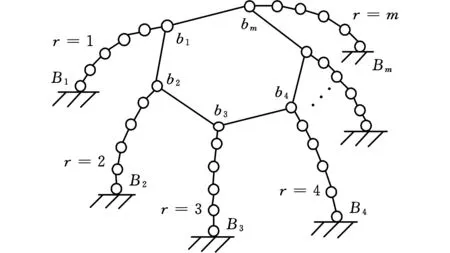
图2 一般空间并联机器人机构示意图Fig.2 Mechanism schematic diagram for general space parallel robot

首先考虑主动关节的原始误差对末端输出位姿的影响。如图3所示，分别建立主动转动关节和主动移动关节的误差分析模型，设初始时刻驱动构件i的理论为值pi，考虑构件存在原始误差Δpi，则该驱动杆件的输入为pi+Δpi，某时刻机器人i驱动的输入为qi，此时，各个分支的主动关节实际参数为di=(pi+Δpi)+qi=pi+(Δpi+qi)。此时，机器人驱动构件的原始误差与其输入误差是等效的。

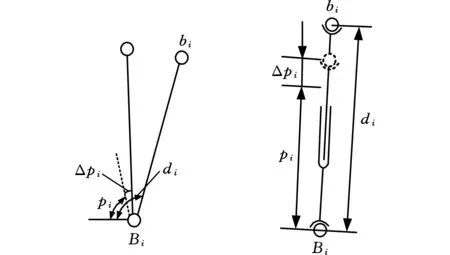
(a)主动转动关节 (b)主动移动关节图3 主动关节误差分析Fig.3 Error analysis for driving joint

一般空间并联机器人的正解模型为

T=f(q)

(1)

q=(q1,q2,…,qm)TT=(α,β,γ,x,y,z)T

其中,T包含了机器人的末端位姿信息。将式(1)对时间求导可得

(2)

令

(3)

式(3)即为一般空间并联机器人的一阶影响系数，由虚位移原理得

(4)

式(4)即为驱动杆件的原始误差与机器人输出位姿误差的映射关系，G为误差映射矩阵。

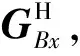
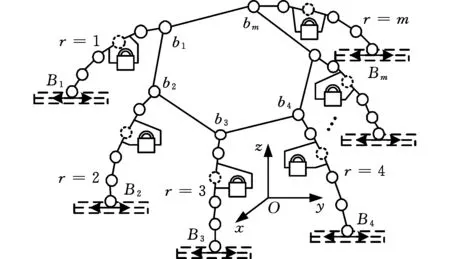
图4 分支下末端关节x向安装误差虚设运动副Fig.4 VJP for assembling error of lower end joints along x axis

按照上述方法可得一般空间并联机器人关键原始误差对机器人输出位姿的误差映射矩阵，如表1所示，其中,右下标b表示对应原始误差源位置,Rx、Ry、Rz表示安装方向。

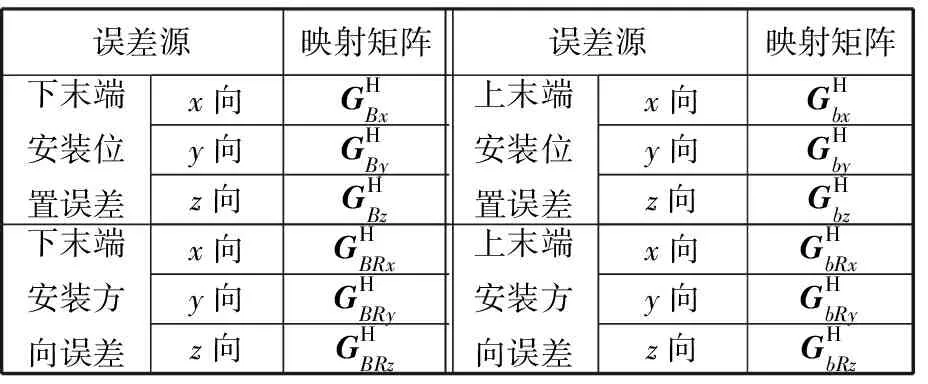
表1 一般空间并联机器人的误差映射矩阵

一般空间并联机器人末端输出位姿的总误差为

(5)

(6)

将式(6)右边第1项记为G，第2项记为E，则

ΔT=GE

(7)

式中，G为总误差映射矩阵；E为误差矩阵。

将式(4)两端同时取行列式得

|ΔT|=|G|·|ΔE|

(8)

式中，|ΔT|为机器人输出位姿误差绝对值；|G|为误差影响因子；|ΔE|为误差绝对值。

1.2误差标定

假设一般空间并联机器人包含的所有误差为6n项，则至少需要n+1组机器人输出位姿才可通过误差映射矩阵求解机器人的位姿误差。图5为采用虚设运动副对一般空间并联机器人的误差标定流程图。在上文提出的误差模型基础上，通过机器人机构反解求出各误差源在理论位姿下的驱动刚化参数，并求出各误差映射矩阵，然后通过最小二乘法求解误差参数并进行补偿。

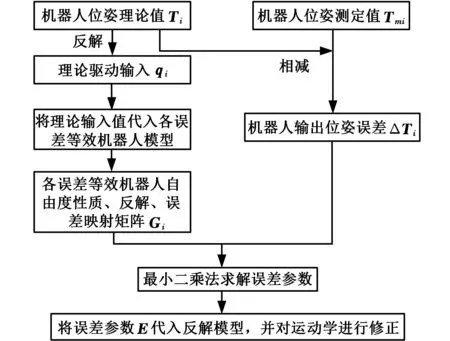
图5 一般空间并联机器人静态误差标定流程图Fig.5 Flow chart of calibration static error for general space parallel robot

设机器人测定位姿Tmi(i=1,2，…，k)为k组(k>n+1)，将对应的位姿理论值Ti代入机器人运动学反解，得到理论输入值qi，将理论输入值qi代入上述各误差等效机器人模型，并分析各等效机器人的自由度性质、反解和误差映射矩阵Gi。综合考虑机器人输出位姿误差ΔTi和各误差映射矩阵Gi，得到

(9)

写成矩阵形式为

(10)

即

ΔTcb=GcbE

(11)

运用最小二乘法求解上述方程得

(12)

将求得的误差参数E代入机器人反解模型，并对机器人运动学模型进行修正。上述为基于虚设运动副对一般空间并联机器人的静态误差建模与标定。通过分析可见，该误差建模方法的物理意义明确，运算操作便捷，具有良好的实用性。

2 基于虚设运动副的3-P(4S)并联机器人误差建模

2.13-P(4S)并联机器人机构

3-P(4S)并联机器人三维实体造型如图6所示。该机器人由动平台、基座以及连接二者的三条分支组成。每条分支均为P(4S)结构，即一个移动副和四个球副，四个球副组成一个平行四边形子闭环。移动副选用直线电机，并以圆周对称的形式安装于基座。4S子闭环的两个下球副与移动副连接，两个上球副与动平台连接。

图6 3-P(4S)并联机器人三维造型Fig.6 3D rending model of 3-P(4S) parallel robot

2.1.1自由度分析

3-P(4S)并联机器人结构见图7，{M}为与动平台固接的坐标系，{O}为与定平台固接的坐标系,{Di}(i=1,2,3)为各分支坐标系。Ra为动平台铰链点Aij所在圆周半径，Rb为移动副基准点Bi所在圆周半径。ui为驱动输入。

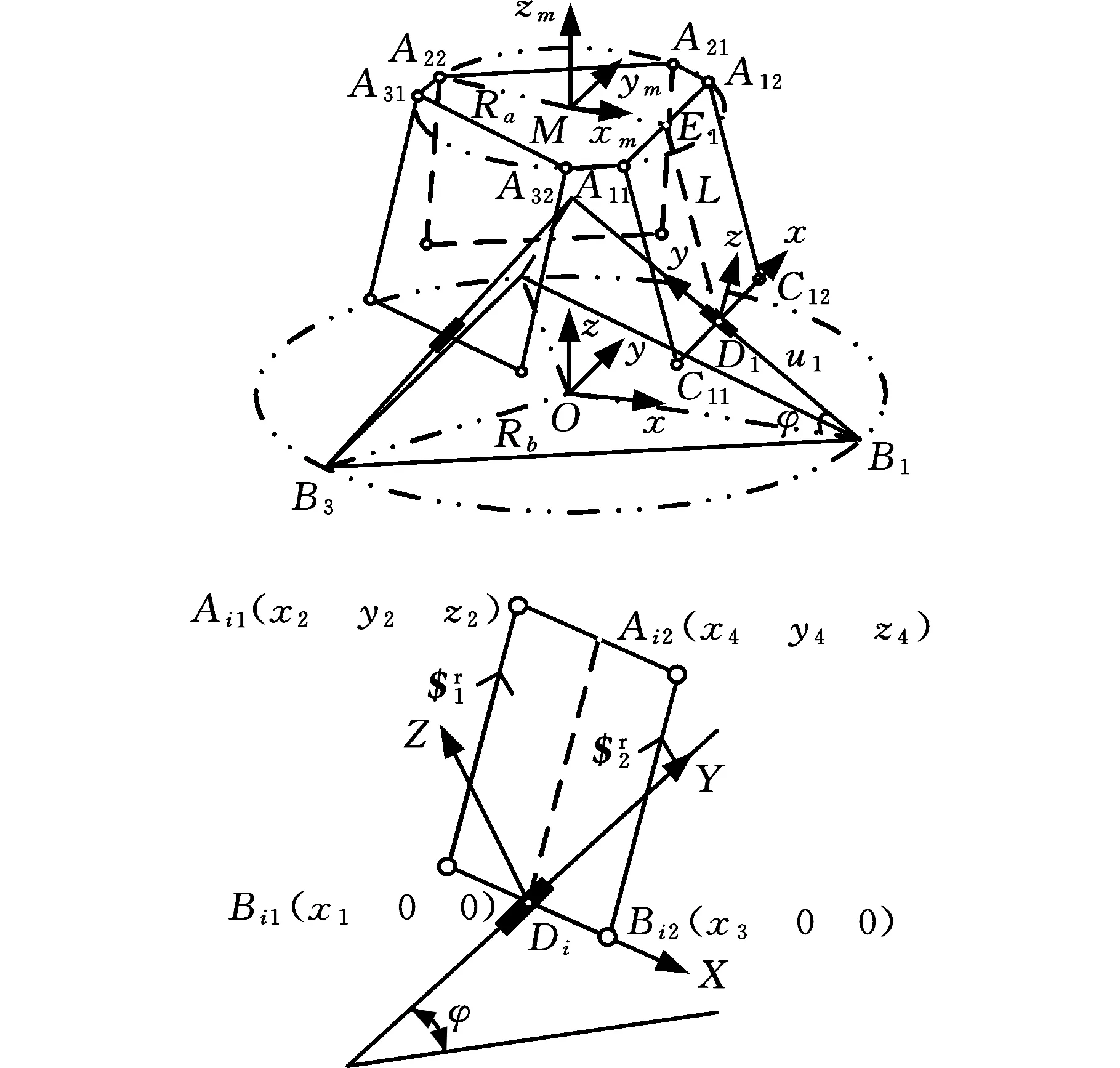
图7 3-P(4S)并联机器人及分支结构简图Fig.7 Structure diagram of 3-P(4S) parallel robot and branches

根据约束螺旋理论[17-18]，4S子闭环可等效为一广义运动副。子闭环的约束螺旋为

(13)

式中，(xk，yk，zk)是4个球副在{Di}中的坐标值，k=1,2,3,4。

可见，4S子闭环提供的约束是两个力线矢，方向分别沿杆Ci1Ai1和Ci2Ai2。

由于4S子闭环为平行四边形即Ci1Ai1∥Ci2Ai2，故有

(14)

将式(14)代入式(13)的反螺旋，同时考虑分支原倾斜布置的驱动移动副，则分支的运动螺旋系在{Di}系的表示式为

(15)

由式(15)可知，分支运动螺旋系为五系螺旋，对其求反螺旋可得到分支的约束螺旋为

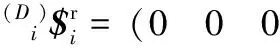
(16)

这是一个轴线垂直4S子闭环平面的力偶。3个分支各提供一个同等形式的约束力偶，且在一般位置，3个力偶线性无关，因此约束了机器人所有转动自由度，因此该3-P(4S)并联机器人具有3个移动自由度。

2.1.2运动学反解

由于Ai1Ai2中点与Ci1Ci2中点的连线EiDi的长度L不变，故

L=|OEi-ODi|

(17)

式中，OEi、ODi分别为Ei、Di点在{O}系的坐标向量。

给定一组机器人输出位姿参数M=(xm,ym,zm)T，OEi能够确定，通过式(17)进行反解运算，可求得驱动输入u=(u1，u2，u3)T。

该机器人实际加工和装配调试中发现，其移动驱动副误差和子闭环安装座的两个位置误差对机器人输出位姿影响较明显。以这三个原始误差源为例，基于本文提出的虚设运动副法对3-P(4S)并联机器人进行误差建模分析与标定实验研究。

2.1.3工作空间分析

单分支内结构参数如图8所示，其中OB1=699.7736 mm，ME1=201.2461 mm，D1E1=376 mm，umax=90 mm，3个分支互成120°。球副转角范围为±16°，当ui=umin=-40 mm和ui=umax=40 mm时分别得到工作空间最低点zmmin和最高点zmmax。根据驱动器行程以及约束条件，通过式(17)进行反解搜索，计算每一zm处动平台在xy平面内的边界值，最终得到动平台工作空间，如图9所示，x轴方向位移输出为±95 mm，y轴方向位移输出为±89 mm，z轴方向位移输出为±33 mm。

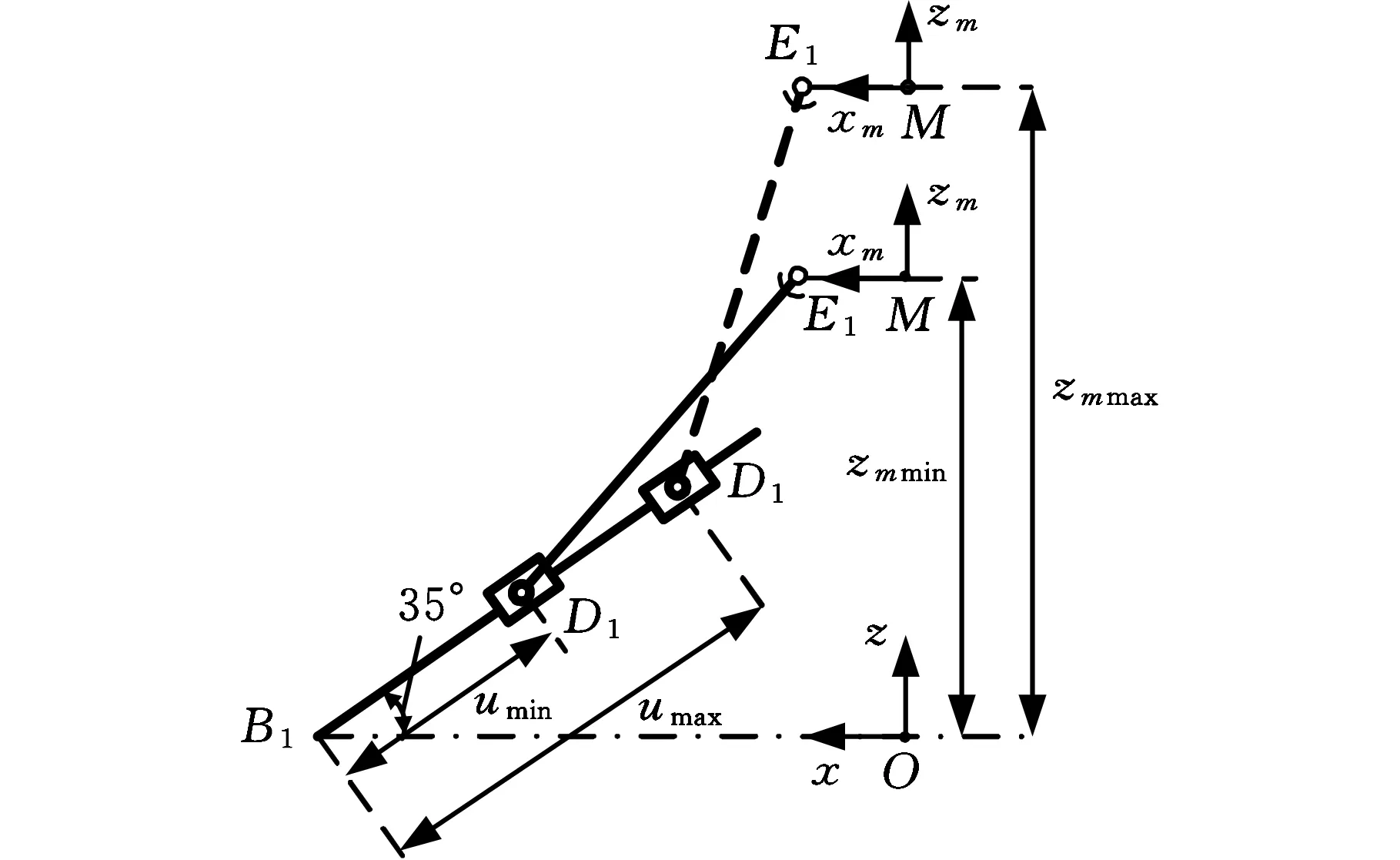
图8 分支结构参数Fig.8 Structure parameters of limbs

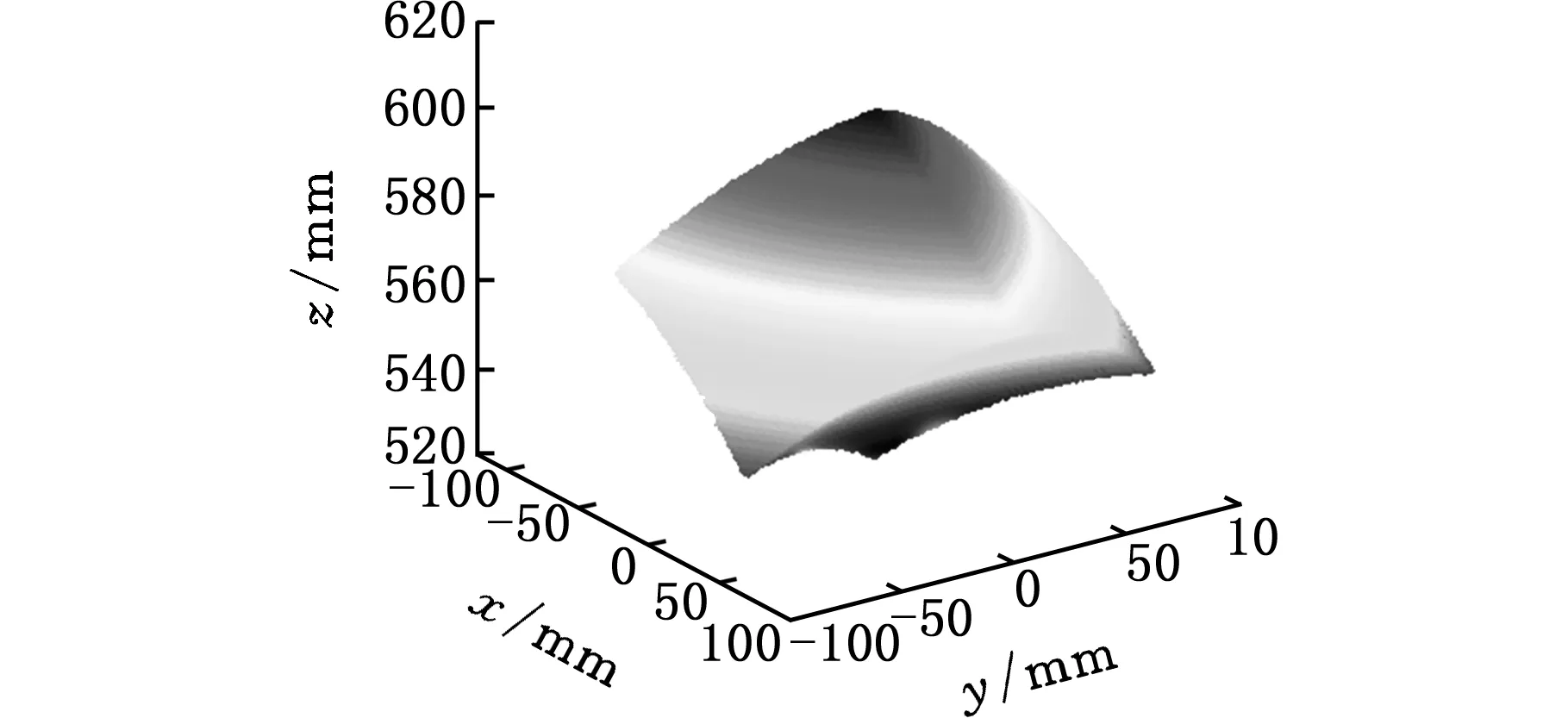
图9 3-P(4S)并联机器人工作空间分析Fig.9 Workspace of 3-P(4S) parallel robot

2.2移动驱动副的误差建模

2.2.1等效机器人机构分析

考虑移动驱动副的位置误差时，如图10所示，需刚化原有的驱动，根据误差建模的虚设运动法，此时需虚设一个沿原驱动方向的移动副，并将其虚设为新的驱动，构建得到等效机器人机构，由于等效机器人的虚设驱动和原机器人驱动共线，所以原机器人的自由度性质和反解也同样适用于等效机器人。

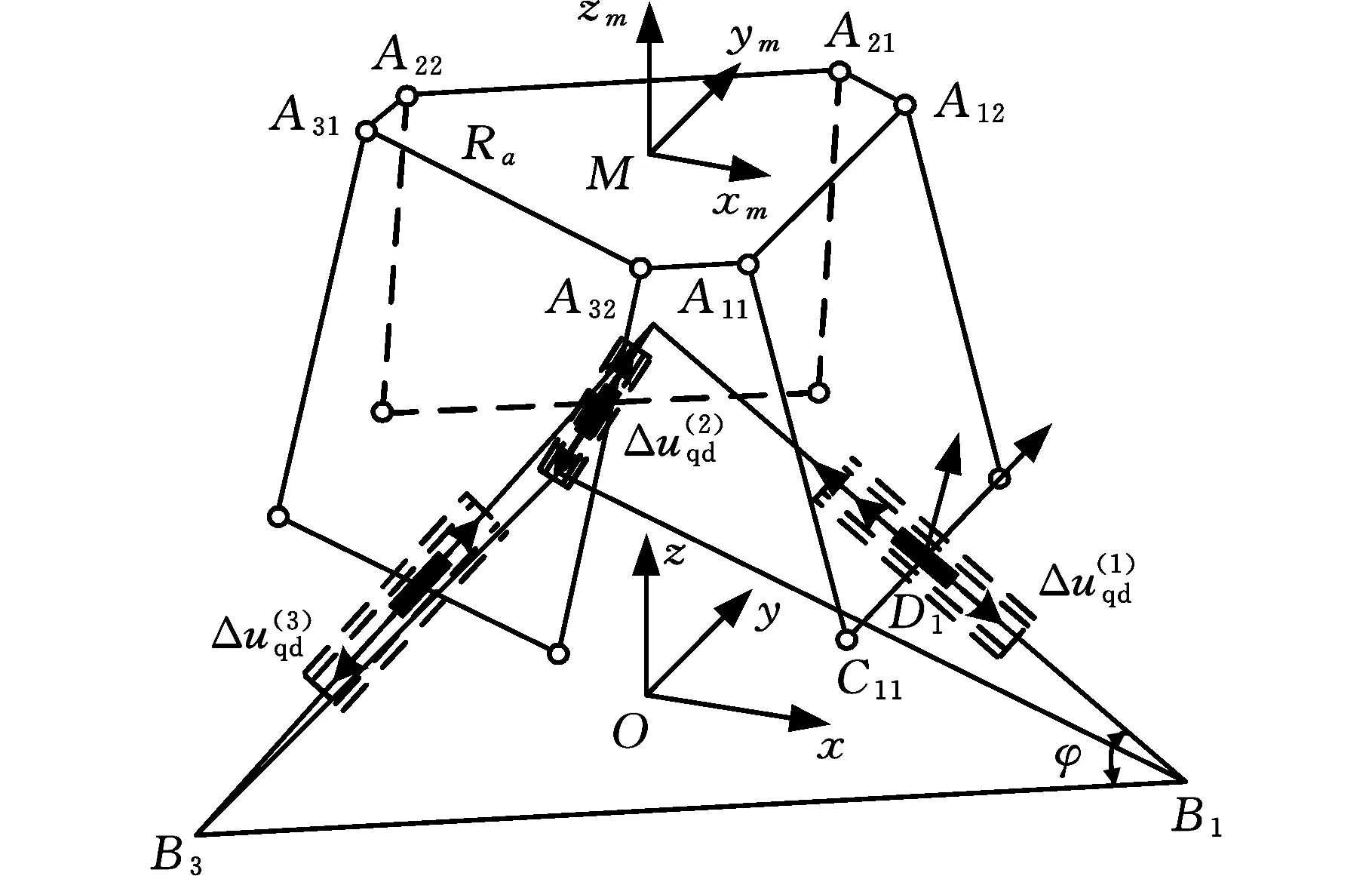
图10 考虑移动驱动副误差等效机器人机构简图Fig.10 Mechanism diagram of equivalent robot considering error of the actuators

2.2.2等效机器人机构误差映射矩阵

为求该少自由度等效机器人的误差映射矩阵，每个分支还需虚设与式(15)运动螺旋系线性无关的运动副使等效机器人分支自由度为6，这里虚设沿{Di}系z轴方向的转动驱动副，该转动副运动螺旋在{Di}系表示为

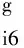
分支运动副的运动螺旋系在{O}系中的表示为

(18)

(Di)$i=

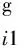
(Oi)$i=

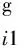
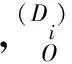
由误差映射矩阵Δu=G[Δφ1Δφ2…

Δφ6]T可知，[Δφ1Δφ2… Δφ6]T=G-1Δu。

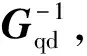
(19)

将式(19)两端同时乘以Gqd，可得

(20)

2.3子闭环安装座的位置误差建模

若考虑子闭环安装座的位置误差，每个安装座的位置在{Di}系中有x、z两个方向的误差。以x向误差为例，如图11所示，刚化原有的驱动，虚设沿{Di}系x向的移动副并将其设为驱动。此等效机器人的自由度分析、运动学反解和误差映射矩阵的求解过程和上述移动驱动副相同，这里不再赘述。

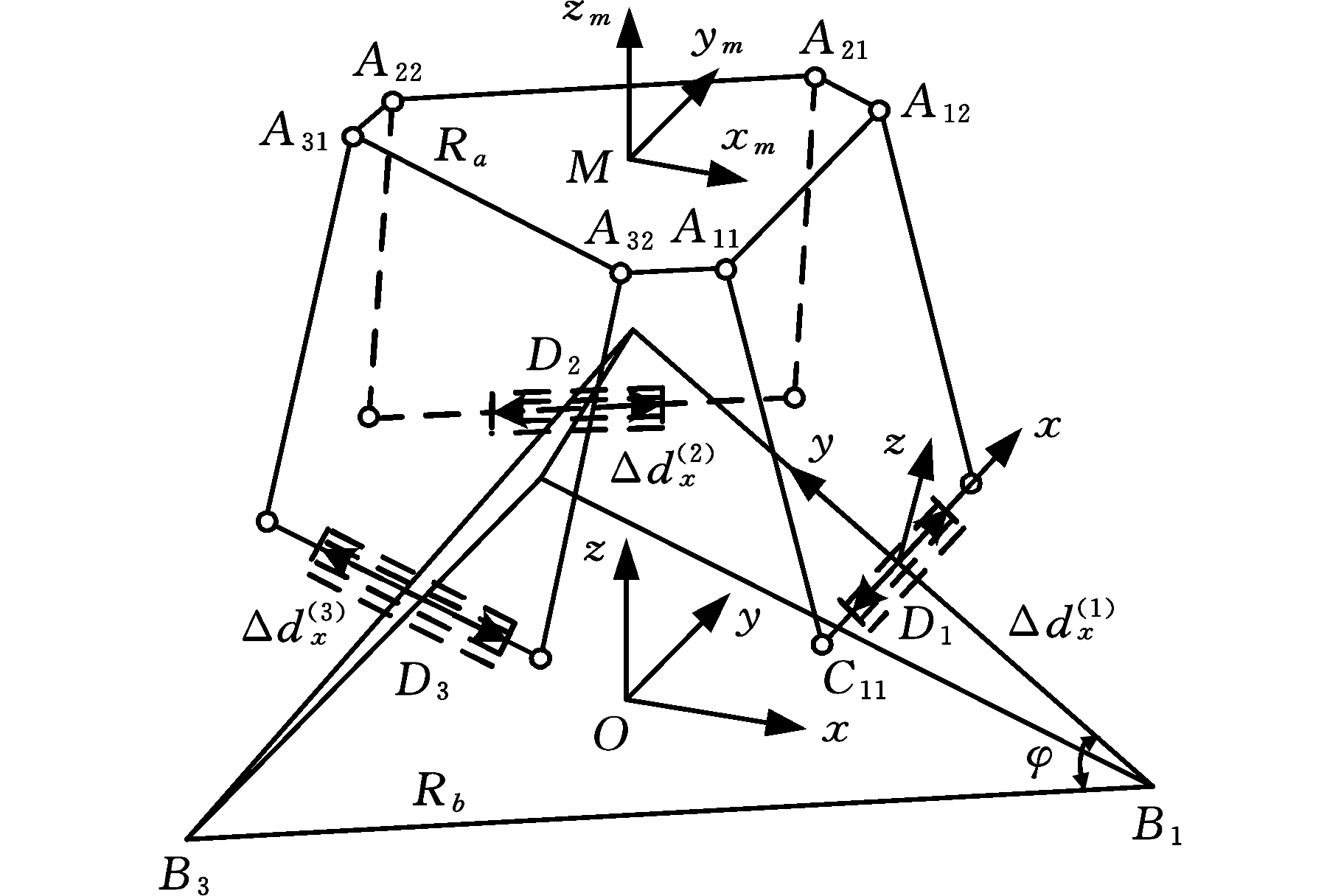
图11 子闭环安装座x向误差的等效机器人简图Fig.11 Mechanism diagram of equivalent robot for base error along x axis of child closed-loop

该等效机器人的误差映射矩阵记为GDx，其误差映射关系为ΔTDx=GDxΔdx，同理得到z向误差映射矩阵GDz，其误差映射关系为ΔTDz=GDzΔdz。

2.4误差影响因子分析

为研究该机器人移动驱动副误差、子闭环安装座的位置误差在整个工作空间中的影响因子大小，分别给定机器人末端输出构件相对{O}系三个理论单轴运动轨迹方程：

x=10sinπtmm,y=z=0
y=10sinπtmm,x=z=0
z=20sinπtmm,x=y=0

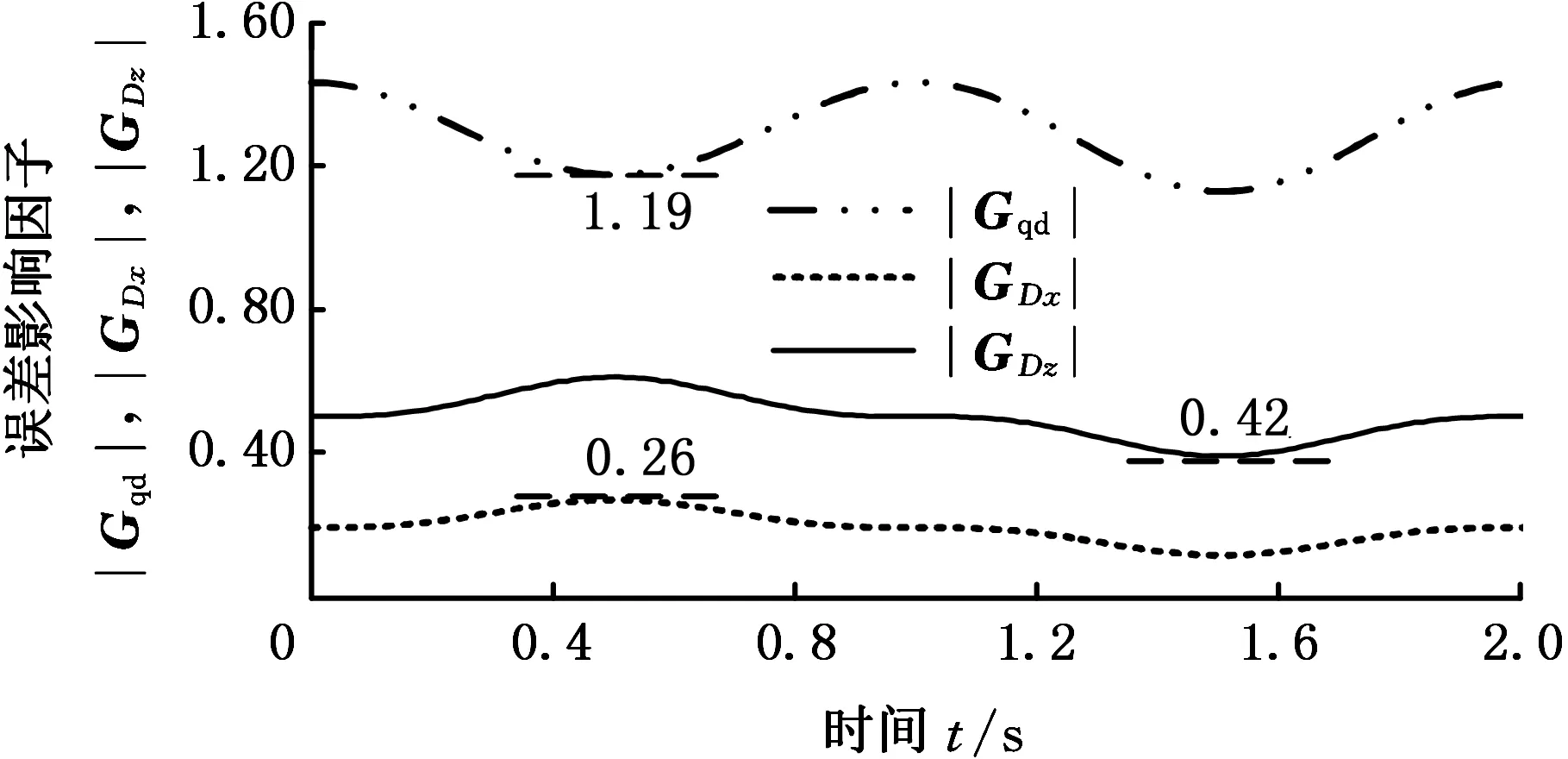
利用MATLAB仿真，绘制在给定理论单轴运动下的三个误差影响因子变化曲线，如图12所示。

(a)x向单轴运动

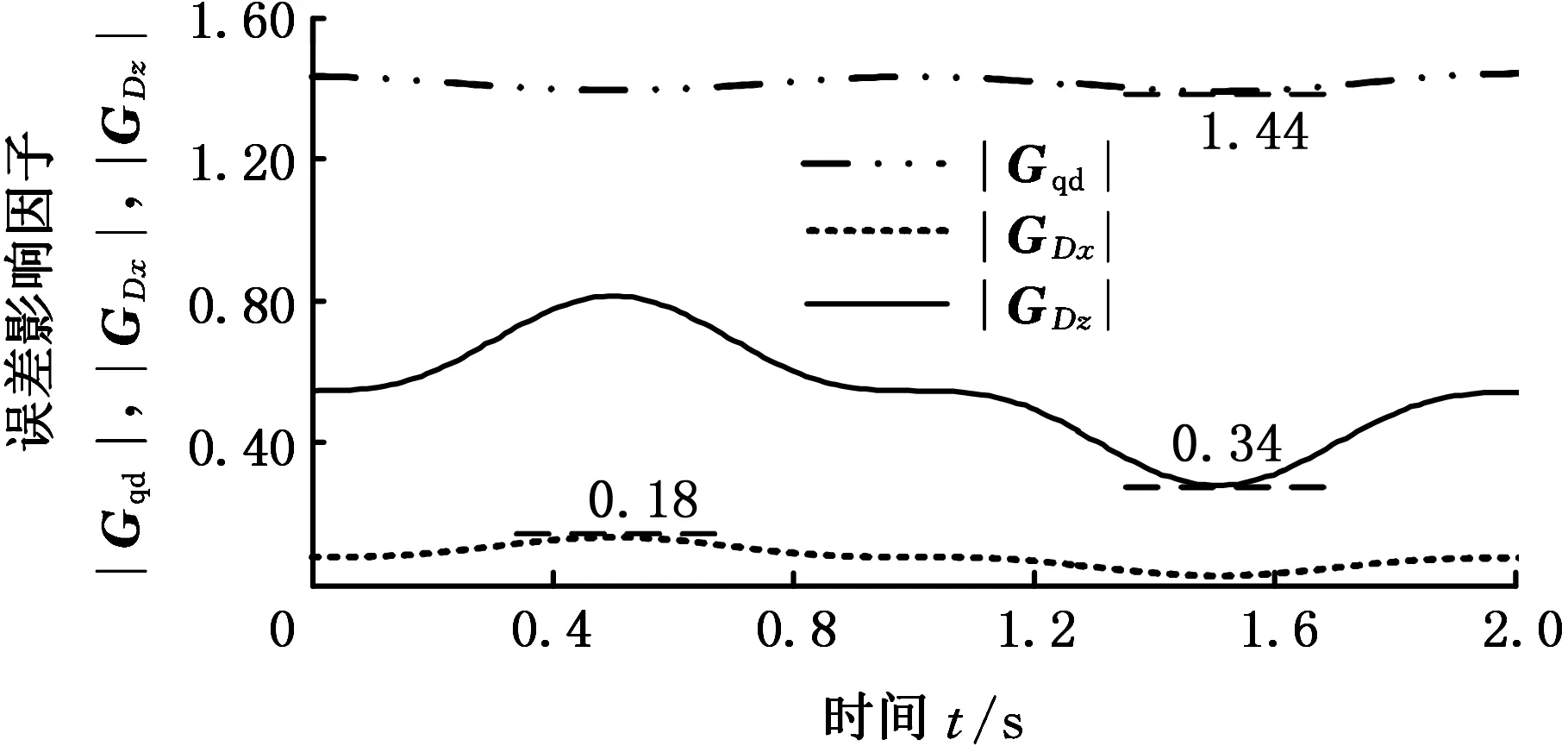
(b)y向单轴运动

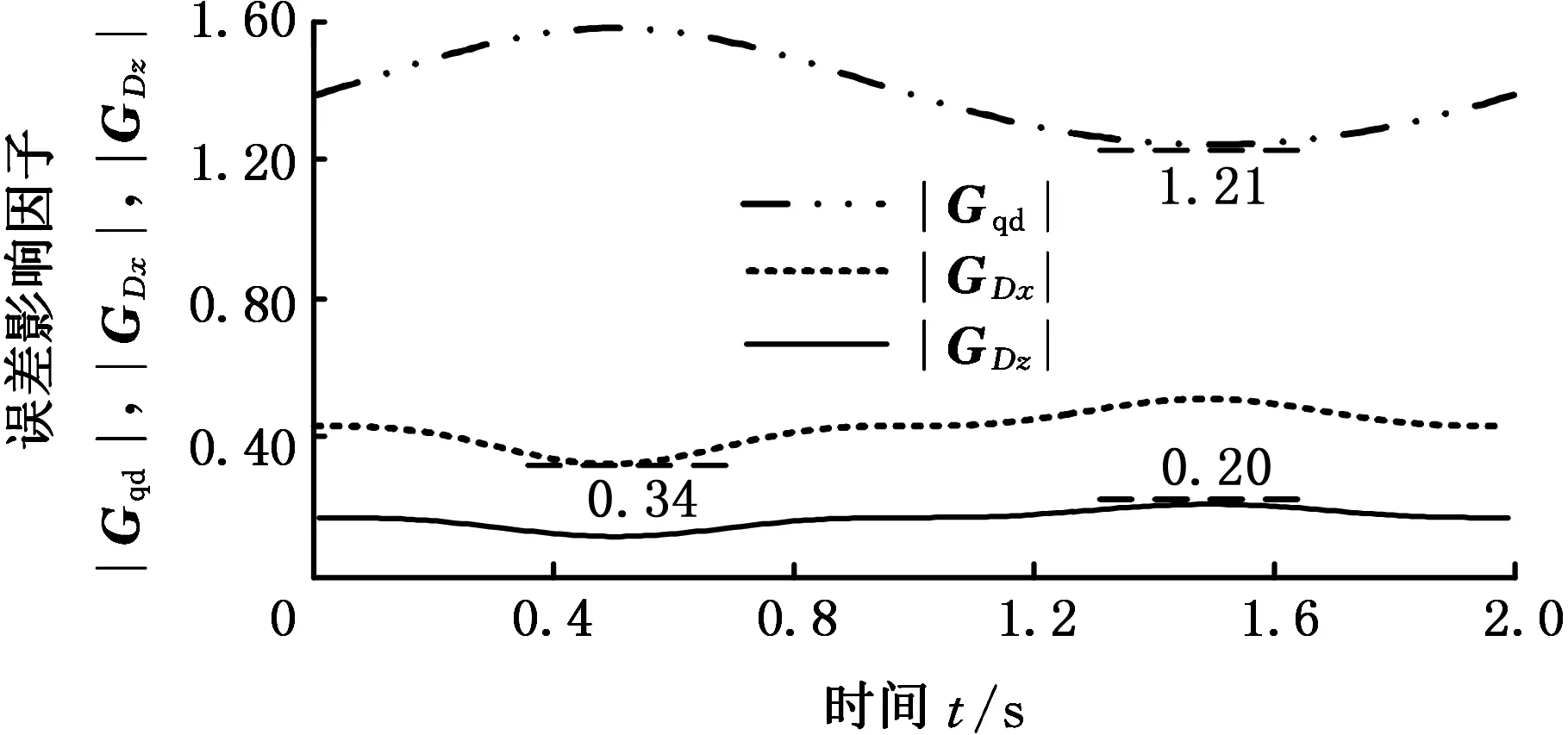
(c)z向幅值20 mm图12 单轴运动误差影响因子变化曲线Fig.12 Error impact factor curve for single-axis motion

由图12可知，单轴运动时，移动驱动副的误差影响因子|Gqd|的最小值分别为1.19、1、44和1.21，均比子闭环安装座在{Di}系的位置误差影响因子|GDx|、|GDz|大，可见单轴运动时，机器人末端输出精度对移动驱动副误差最敏感；x向和y向单轴运动时，|GDx|的最大值分别为0.26和0.18，小于|GDz|的最小值0.42和0.34，此时机器人末端输出精度对安装座z向位置误差比安装座x向位置误差更敏感；z向单轴运动时，|GDz|的最大值为0.20，小于|GDx|的最小值0.34，此时机器人末端输出精度对安装座x向位置误差比安装座z向位置误差更敏感。

给定机器人末端输出构件三轴复合运动，运动轨迹方程如下：

x=10sinπtmmy=10sinπtmm
z=20sinπtmm

通过仿真绘制复合运动下的三个误差影响因子变化曲线，如图13所示。

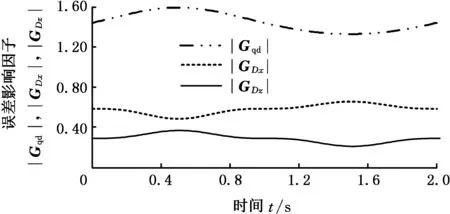
图13 复合运动误差影响因子变化曲线Fig.13 Error impact factor curve for composite motion

由图13可知，在整个给定理论位姿中，驱动误差影响因子|Gqd|均比安装座位置误差影响因子|GDx|和|GDz|大，即该3-P(4S)并联机器人末端输出位姿误差对驱动误差相比安装定位误差更为敏感，在加工制造中需要特意提高移动驱动副的精度才能保证机器人末端输出位姿的精度。

3 基于虚设运动副的3-P(4S)并联机器人静态误差标定

基于上文采用虚设运动副建立的3-P(4S)并联机器人误差源误差模型，下文对3-P(4S)并联机器人进行静态误差标定。

首先在上节求得的工作空间内选取10个标定测量点，标定测量点的选取原则是尽可能地分布在机构的整个工作空间。利用激光跟踪仪检测出3-P(4S)并联机器人的实际运动输出位姿信息。测量激光跟踪仪原点在{O}系中的坐标值，通过坐标转换，得到这些测量点在{O}系中的坐标理论值和误差值，如表2所示。

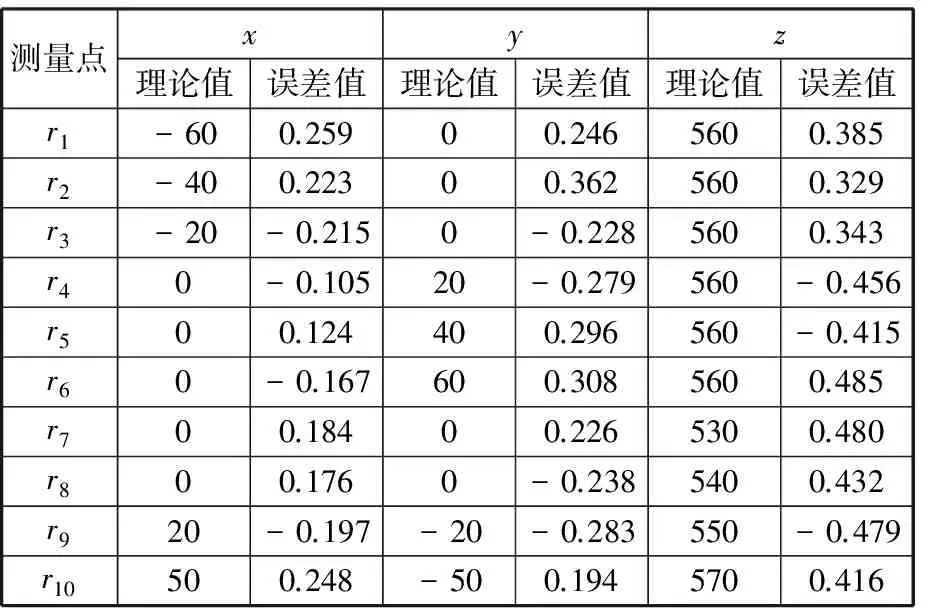
表2 3-P(4S)并联机器人输出位姿理论值和误差值

将机器人输出的位姿理论值M=(xm,ym,zm)T代入反解模型式(17)，求解出机器人的理论驱动输入值u，将其作为三个误差等效机器人的原驱动刚化参数代入等效机器人模型，并求解出误差映射矩阵Gqd、GDx和GDz。

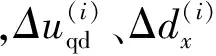
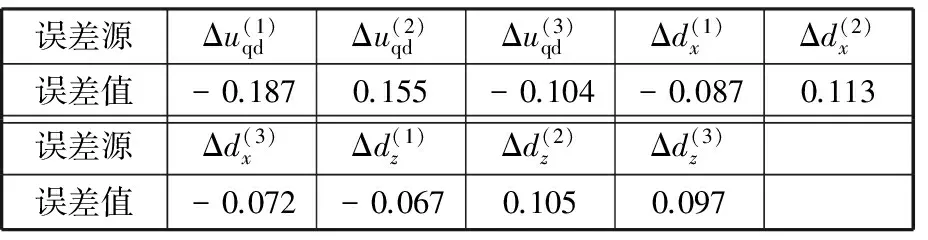
表3 各原始误差值

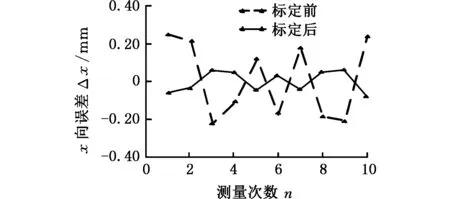
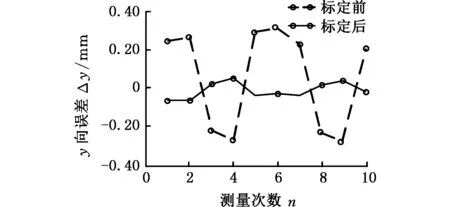
将上述各原始误差值代入机器人模型，对机器人运动学模型进行修正，用修正后的反解，控制机器人运动至原先选定的测量点，记录此时各个测量点的实际坐标值，将测量点修正前后的位姿误差数据绘制曲线，得到图14所示的各方向的位姿误差对比曲线图。

(a)x向定位误差

(b)y向定位误差

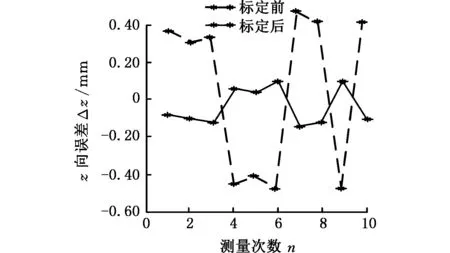
(c)z向定位误差图14 标定前后单向定位误差对比图Fig.14 Error comparison charts for before and after calibrating along single-direction

由图14可知，标定后x、y、z向定位误差的平均值、最大值和标定前相比均降低。将同一测量点的x向、y向、z向定位误差组合成向量并求模，得到图15所示的标定前后体积误差[19]对比图。

由图15可知，标定前体积误差平均值为0.523 mm，最大值为0.585 mm，标定后体积误差平均值为0.118 mm，最大值为0.142 mm。通过实验结果表明，采用文中提出的虚设运动法对并联机器人进行误差识别补偿后的定位精度得到了较大的提高，该误差建模和标定方法是切实有效的。

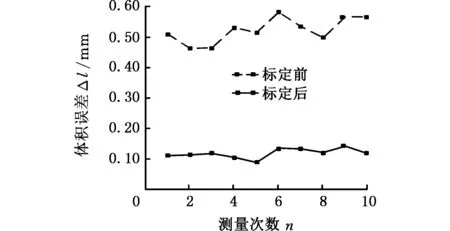
图15 标定前后体积误差对比图Fig.15 Volumetric error comparison chart for before and after calibrating

4 结论

(1)提出了一种基于虚设运动副的并联机器人静态误差建模和标定通用新方法，详述了通过虚设运动副建立一般空间并联机器人的静态误差模型，并推导了一般空间并联机器人的标定过程。

(2)对3-P(4S)并联机器人的自由度、运动学反解、工作空间进行分析，采用虚设运动副法对3-P(4S)并联机器人的驱动副误差和子闭环安装座的x、z向位置误差进行了误差建模，建立对应误差源的误差映射矩阵，并给定不同的运动轨迹方程得到各误差的影响因子，对实践加工起到指导作用。

(3)对3-P(4S)并联机器人驱动副误差和子闭环安装座的位置误差进行了标定分析。标定实验表明，基于该方法标定后输出定位误差均值由0.523 mm降低到0.142 mm，机器人的静态定位精度明显提高。

[1] 牛亚雯, 冯志友. 温淑鸿. 基于正交设计的2UPS-RPU并联机构误差分析[J]. 机械设计,2015, 32(1):30-34. NIU Yawen, FENG Zhiyou, WEN Shuhong. The 2UPS-RPU Parallel Mechanism Error Analysis Based on the Orthogonal Design[J]. Machine Design, 2015,32(1):30-34.

[2] 周学才, 张启先. 机器人位姿误差的显著性分析法[J]. 机械工程学报,1994,30(增1): 167-175. ZHOU Xuecai, ZHANG Qixian. The Significance of Analysis for Robot Position and Pose Error [J]. Journal of Mechanical Engineering, 1994,30(S1): 167-175.

[3] 黄真, 孔令富， 方跃法. 并联机器人机构学理论及控制[M].北京：机械工业出版社, 1997. HUANG Zhen, KONG Lingfu, FANG Yuefa. Parallel Robot Mechanism Theory and Control[M]. Beijing：China Machine Press, 1997.

[4] 方跃法. 并联机器人误差分析[D].秦皇岛：燕山大学, 1987. Fang Yuefa. Error Analysis of Parallel Robot[D]. Qinhuangdao: Yanshan University, 1987.

[5] 黄真, 方跃法. 六自由度并联机器人的随机位姿误差分析[J]. 东北重型机械学院学报, 1989, 13(3):1-9. HUANG Zhen, FANG Yuefa F. Random Position and Pose Error Analysis of Six DOF Parallel Robot[J]. Journal of Northeast Institute of Heavy Machinery, 1989, 13(3):1-9.

[6] 李永泉, 张立杰, 郭志民, 等. 基于D-H矩阵的球面5R并联机构误差建模及灵敏度分析[J]. 中国机械工程, 2012, 23(12): 1470-1474. LI Yongquan, ZHANG Lijie, GUO Zhiming, et al. Error Modelling and Sensitivity Analysis of Spherical 5R Parallel Manipulator Based on D-H Matrix[J]. China Mechanical Engineering, 2012, 23(12): 1470-1474.

[7] 曲云霞,杨少辉,秦玉霞，等. 一种两自由度球面解耦并联机构位姿误差分析[J]. 机械设计, 2008, 25(8): 36-38. QU Yunxia, YANG Shaohui, QIN Yuxia, et al. Posture Error Analysis on a Kind of Parallel Mechanism with Two DOF Spherical Surfaced Decoupling[J]. Machine Design, 2008, 25(8): 36-38.

[8] 黄田, 李亚, 李思维, 等. 一种三自由度并联机构几何误差建模、灵敏度分析及装配工艺设计[J]. 中国科学(E辑), 2002, 35(12):628-635. HUANG Tian, LI Ya, LI Siwei, et al. Geometric Error Modelling, Sensitivity Analysis and Assembly Process Design for a Three DOF Parallel Mechanism [J]. Science in China(Serices E), 2002, 35(12):628-635.

[9] SIAMAK P, MOHAMMAD R C Q, Hamid A, et al. Mathematical Modelling of Linear Motion Error for Hexarot Parallel Manipulators[J]. Applied Mathematical Modelling, 2016.40(8):942-954.

[10] ZI Bin , DING Huafeng, WU Xia. et al. Error Modeling and Sensitivity Analysis of a Hybrid-driven Based Cable Parallel Manipulator[J]. Precision Engineering， 2014，38(1):197-211.

[11] 李嘉, 王纪武, 陈恳. 基于广义几何误差模型的微机器人精度分析[J]. 机械工程学报，2000,36(8):20-24． LI Jin, WANG Jiwu, CHEN Ken. Accuracy Analysis of Micro-robot Based on Generally Geometric Error Model[J]. Journal of Mechanical Engineering, 2000,36(8):20-24．

[12] YAO Rui, ZHU Wenbai, HUANG Peng. Accuracy Analysis of Stewart Platform Based on Interval Analysis Method[J]. Chinese Journal of Mechanical Engineering, 2013,29(1):29-34.

[13] WANG S M, EHMANN K F. Error Modling and Accuracy Analysis of a Six-DOF Stewart Platform[J]. Joural of Manufacturing Science and Engineering, 2002,124(2):286-295.

[14] 李新友, 陈五一, 韩先国. 基于正交设计的3-RPS并联机构精度分析与综合[J]. 北京航空航天大学学报, 2011,37(8):979-984. LI Xinyou, CHEN Wuyi, HAN Xianguo. Accuracy Analysis and Synthesis of 3-RPS Parallel Machine Based on Orthogonal Design[J]. Journal of Beijing University of Aeronautics and Astronautics, 2011,37(8):979-984.

[15] 刘红军, 龚民, 赵明扬, 等. 一种四自由度并联机构的误差分析及其标定补偿[J]. 机器人, 2005, 27(1): 6-9. LIU Hongjun, GONG Ming, ZHAO Mingyang, et al. Error Analysis and Calibration of a 4-DOF Parallel Mechanism[J]. Robot, 2005, 27(1): 6-9.

[16] 谭兴强, 张键, 谢志江. 风洞6_PUS并联支撑机器人运动误差建模与补偿[J]. 农业机械学报, 2014, 45(4):334-340. TANG Xingqiang, ZHANG Jian, XIE Zhijiang. 6_PUS Parallel Robot Motion Error Modeling and Compensation for Wind Tunnel[J]. Journal of Agricultural Machinery, 2014, 45(4):334-340.

[17] 黄真, 刘婧芳, 曾达幸. 基于约束螺旋理论的机构自由度分析的普遍方法[J]. 中国科学(E辑)，2009, 39(1): 84-93. HUANG Zhen, LIU Jinfang, ZENG Daxing. A General Method for Mechanism DOF Analysis Based on Constraint Screw Theory[J]. Science in China(Serices E), 2009, 39(1): 84-93.

[18] 黄真, 赵永生, 赵铁石. 高等空间机构学[M]. 北京: 高等教育出版社, 2006. HUANG Zhen, ZHAO Yongsheng, ZHAO Tieshi. Advanced Spatial Mechanism[M]. Beijing: Higher Education Press, 2006.

[19] 唐国宝, 黄田.Delta并联机构精度标定方法研究[J]. 机械工程学报,2003, 39(8): 55-64. TANG Guobao, HUANG Tian. Kinematic Calibration of Delta Robot[J]. Journal of Mechanical Engineering, 2003, 39(8): 55-64.

(编辑郭伟)

StaticErrorModellingandCalibrationforParallelRobotsBasedonVirtualJointPairs

ZHAO Yanzhi1,2SONG Xiaoxin1,2YANG Jiangtao1,2QI Lizhe3HE Yong1，4ZHAO Tieshi1,2
1.Hebei Provincial Key Laboratory of Parallel Robot and Mechatronic System,Yanshan University,Qinhuangdao，Hebei,066004 2.Key Laboratory of Advanced Forging & Stamping Technology and Science,Ministry of National Education,Yangshan University,Qinhuangdao，Hebei,066004 3.InterSmart Robotic systems Co.,Ltd.,Tianjin,301700 4.Shenzhen Institutes of Advanced Technology,Chinese Academy of Sciences,Shenzhen，Guangdong,518055

Based on the principles of parallel robot influence coefficient and virtual displacement, a case analysis of general space parallel robot, a new generalized method for parallel robot static error modelling was proposed by virtual joint pairs(VJP). The independent effects of each original processing assembly sources of errors for the end-pose were determined, the physical meaning of the proposed method was clear and the modelling and analysis processes were convenient. Based on this, taking 3-P (4S) parallel robot as the research object, the mapping matrix of each error sources was obtained by VJP, and the error calibrations of robots were conducted. The experimental results show that the maximal positioning error is decreased from 0.585mm to 0.142mm, accuracy of the robot outputs after calibrations is improved significantly than that without calibrations based on this method, and the effectiveness of the method was validated further.

parallel robot; static error modelling; virtual joint pair; error mapping matrix

TP24

10.3969/j.issn.1004-132X.2017.18.007

2016-10-17

国家自然科学基金资助项目(50975244)；河北省自然科学基金资助项目(E2014203176)；河北省高等学校自然科学研究基金资助项目(QN2015040)；中国博士后科学基金资助项目(2016M590212)

赵延治，男，1981生。燕山大学机械工程学院副教授、博士。研究方向为并联机器人机构学理论与应用、多维力加载与测量技术。E-mail：yzzhao@ysu.edu.cn。宋晓鑫，男，1992生。燕山大学机械工程学院硕士研究生。杨建涛，男，1987生。燕山大学机械工程学院硕士研究生。齐立哲，男，1981生。天津智通机器人系统有限公司高级工程师。何勇，男，1987生。燕山大学机械工程学院硕士研究生，中国科学院深圳先进技术研究院工程师。赵铁石，男，1963生。燕山大学机械工程学院教授、博士研究生导师。