水平轴风力机的转矩性能及叶尖损失对其的影响

姜海波 李艳茹 赵云鹏

海军工程大学勤务学院，天津，300450

水平轴风力机的转矩性能及叶尖损失对其的影响

姜海波 李艳茹 赵云鹏

海军工程大学勤务学院，天津，300450

分析了叶尖损失机理，根据PRANDTL 和GLAUERT叶尖损失修正因子及叶素-动量理论，推导出考虑叶尖损失的叶片弦长公式，然后沿叶片展向积分，推导出与风力机尖速比和翼型升阻比关联的风力机转矩系数解析表达式，并得到风力机在任何稳定运行状态转矩系数的最高参数值，可作为风力机转矩系数的设计参考值。研究表明，叶尖损失对弦长的影响集中在叶尖部位，当升阻比为无穷大且尖速比从常见范围10变化到4时，叶尖损失导致转矩性能损失约4%～10%，且损失的数值随升阻比的变化极小。

风能利用；风力机；转矩系数；叶尖损失；叶素-动量理论

0 引言

水平轴风力机最重要的性能指标是功率、转矩和推力。功率系数的研究已有大量文献报道，其中BETZ于1920年给出了风力机功率系数的理论极限是16/27，约为0.593[1-3]。姜海波等[4]则给出了稳定运行状态下与尖速比和升阻比关联的理想风力机功率系数的具体表达式，以及阻力为0(即升阻比为无穷大)时功率的最佳性能公式，并证明只有当尖速比和升阻比均为无穷大时功率系数才会趋近于Betz极限，因此人们就不必为追求超越功率系数理论计算值而花费太多的精力，设计的风力机效率接近相应条件下的理论值时，就可认定是理想设计。

风力机的另一个重要参数是转矩系数，研究转矩系数是否存在理论上的极限值具有十分重要的意义。本文将利用叶素-动量理论通过推导给出风力机最高转矩系数计算公式，对此问题给出肯定的回答。

动量理论假设风力机的叶片数为无穷多，流过风轮的每个空气粒子都与叶片相互作用，但实际风力机的叶片数为有限个，流过风轮的一部分粒子与叶片相互作用，另一部分会穿越叶片之间的空隙。这两种情况下空气传递给风轮的动量是有区别的，即诱导速度不同。如果叶片处的诱导速度很大，那么入流角就会很小，导致转矩在切向的分量减小，从而减小转矩，造成功率损失。本文将在理论叶片弦长的基础上考虑有限叶片数对叶尖损失造成的影响，给出了实际风力机最高转矩性能的计算方法和具体参数值。

1 基本关系式

首先简要考察风力机稳定运行状态(既非加速又非减速的运行状态)，风的作用情况和叶片受力状态(图1、图2)[4]。

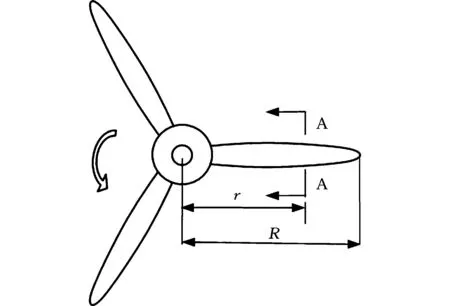
图1 风力机叶轮顺风向示意图Fig.1 Schematic view of a wind turbine with downwind direction

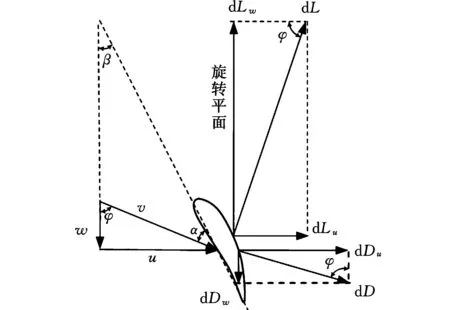
图2 图1之A-A截面叶素风速状态与受力分析Fig.2 Wind speed state and force analysis of the blade element at A-A cross section in Fig. 1

用与转轴同心的圆柱切割叶片，刨面位置见图1的A-A位置，在半径r处取一微段(亦称叶素)dr进行受力分析，如图2所示。设ω为风力机自转角速度，r为叶片展向微段dr到转轴中心的距离，R为叶片的长度。微段dr沿旋转平面向上运动，故存在逆风相对速度W=ωr。W与切向诱导速度bW的合成速度为w=(1+b)W。无穷远处来流绝对速度U与轴向诱导速度aU的合成速度u=(1-a)U是通过叶片的轴向风速，u与w的合成速度v对叶片产生升力和阻力，速度v的攻角为α。升力dL垂直于合成速度v，可分解为周向分量dLw和水平分量dLu；阻力dD与v方向一致，可分解为周向分量dDw和水平分量dDu。φ为v与旋转平面所成的夹角，称来流角或入流角；α为翼弦与v的夹角，称为攻角；设λ为r处W与U的比值，称为线速度比。

对于叶尖损失，PRANDTL等[5]给出了一种近似的修正方法，经过GLAUERT改进后的修正因子为[6]

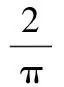
(1)

式中，B为叶片数；λt为尖速比；a为轴向速度诱导因子；x为相对半径，x=r/R。

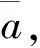
(2)

(3)

叶片局部诱导速度因子为

(4)

(5)

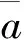
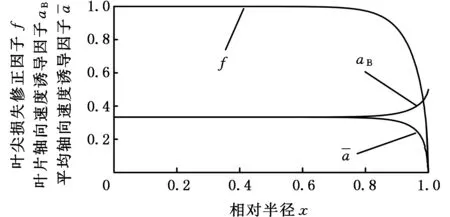
图3 叶尖损失因子与速度诱导因子沿展向的分布曲线Fig.3 Distribution curve of the blade tip loss factor and velocity induction factor along the span

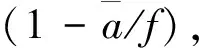
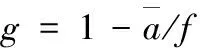
(6)

假定风力机运行在稳定的工况，由图2可知，风的入流速度为

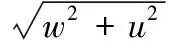
(7)

由此还可以得到入流角的正弦和余弦表达式：

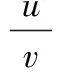
(8)

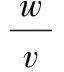
(9)

2 考虑叶尖损失的弦长曲线

根据叶素理论[7]，由图2和式(7)～式(9)可得叶素推力为

dT1=dLu+dDu=dLcosφ+dDsinφ=

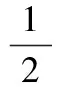
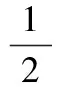
(10)

式中，ρ为空气密度；C为r处翼弦的长度；CL为升力系数；CD为阻力系数。

根据动量理论[8]，来流对风轮圆盘中半径为r到r+dr的圆环的推力为

(11)

每个圆环径跨过B个叶片的叶素，所以dT2=BdT1，可得理想的相对弦长公式为

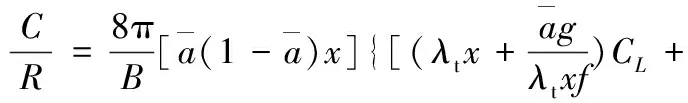
(12)

理想弦长可以通过解析计算的方法得到。从图形来看这种扭曲的形状很难加工生产，强度等性能也不能满足实际流体环境的需要，因此实际叶片必须进行改造(同时也会丧失部分性能)。但是作为理想弦长公式，可以指导设计，并能在理论上发挥重要作用，例如可以利用其推导最高功率、转矩和推力性能公式。

3 最高转矩性能计算

考虑叶尖损失后，根据图2，由式(7)～式(9)可得，稳定运行工况的叶素转矩为

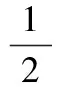
(13)

式中，F为升力的合力。

对于B个叶片组成的风力机，将相对弦长式(12)代入上式积分，得转矩系数为

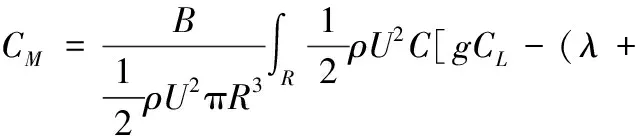
(14)

令阻力系数CD=0(升阻比ζ=∞)，可得到与尖速比关联的转矩系数为

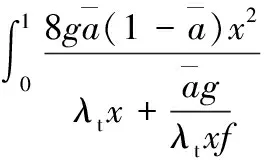
(15)

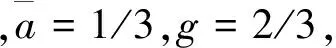
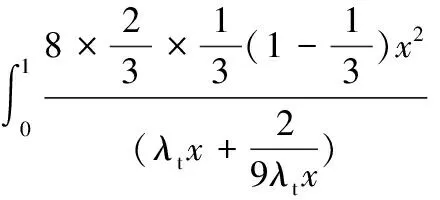
(16)

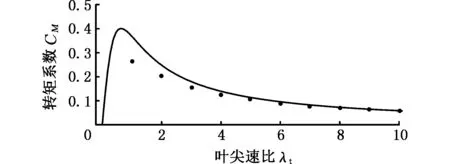
图4 阻力为0时叶尖损失修正后的转矩系数变化趋势Fig.4 Change trend of torque coefficient after correction of blade tip loss when resistance is 0

图4所示为阻力为0但不考虑叶尖损失的最大转矩系数曲线，式(16)和图4的曲线显示阻力为0时风力机具有最高转矩性能，文献[9]推导出相同的结果，但未考虑叶尖损失的影响。将式(1)和式(2)代入考虑叶尖损失影响的式(15)进行数值积分，图4中的点阵所示为叶尖损失修正后的转矩系数变化趋势，点阵和式(15)表明阻力为0时叶尖损失对风力机的最高转矩性能有影响。

由图4可以看出，尖速比较小时，叶尖损失的存在会明显降低转矩系数；升阻比为无穷大时，最高转矩系数损失情况见表1。

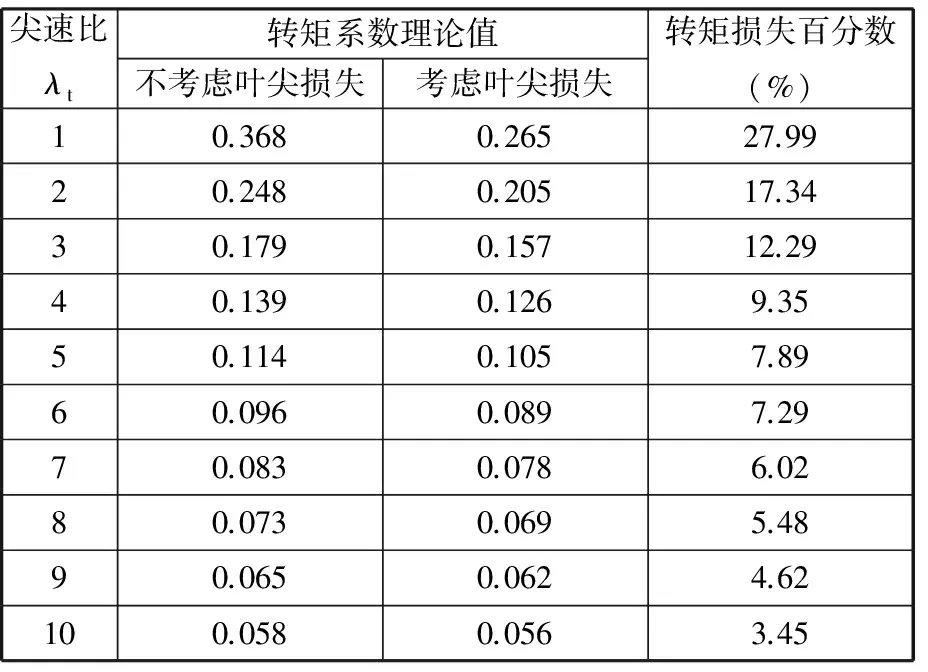
表1 阻力为0时叶尖损失对最高转矩系数的影响

由表1可以看出，不考虑阻力影响的情况下，尖速比从常见范围10变化到4时，叶尖损失导致转矩性能损失约4%～10%。

在实际流体环境，阻力不可能为0(升阻比ζ为有限值)，由式(14)得

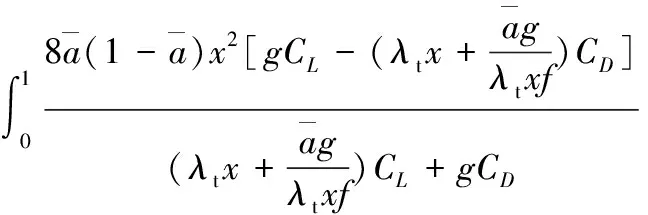
(17)

式(17) 是依据理想弦长公式推导得到的，实际叶片会依据加工难度、结构强度等因素的影响对弦长分布进行修改，被设计加工成简化叶片，从而会降低部分性能，因此式(17)为任何实际风力机能达到的最高转矩性能。

式(17)给定升阻比ζ和尖速比λt一系列参数值后进行数值计算，可得到叶尖损失修正后的最高转矩系数值如表2所示。这些参数值是任何处于稳定运行状态的实际风力机都不可超越的极限。

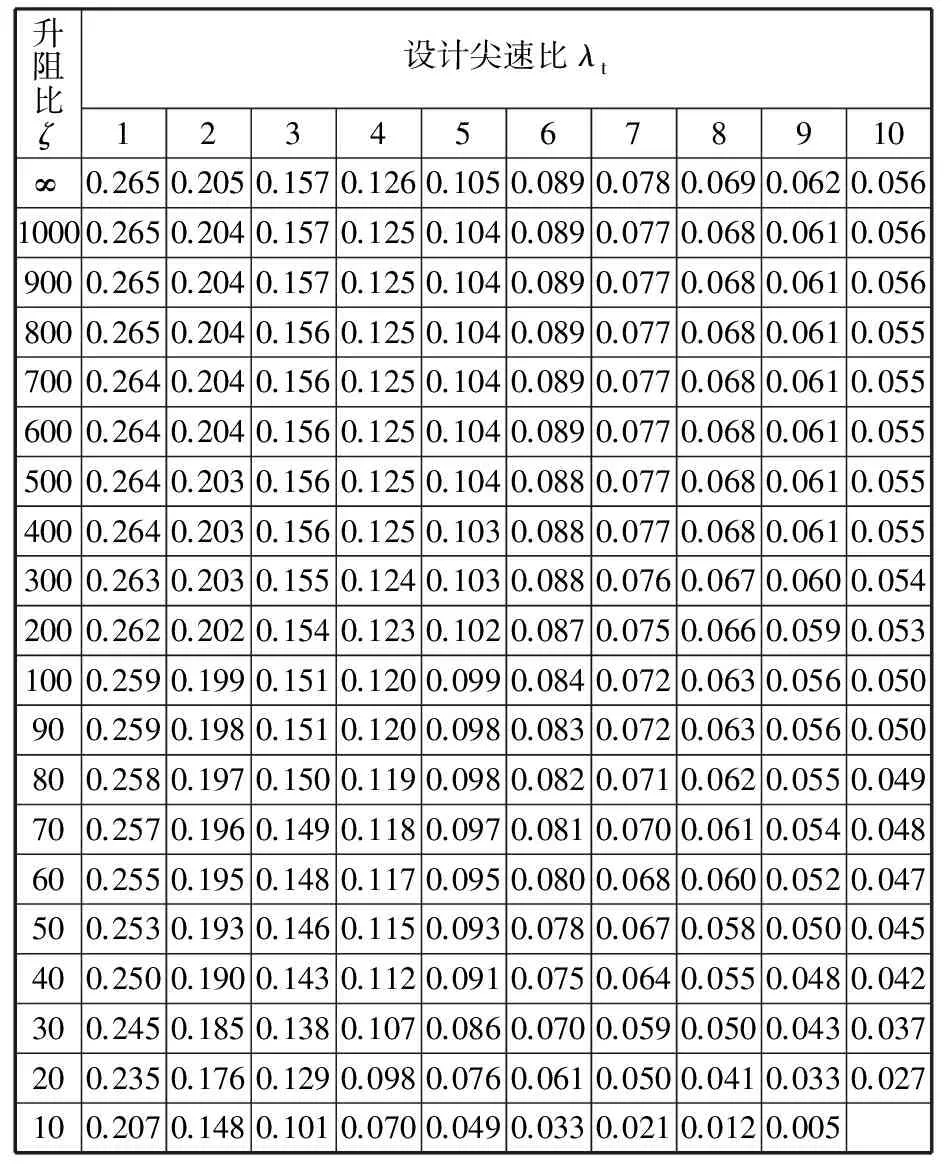
表2 叶尖损失修正后的最高转矩系数值

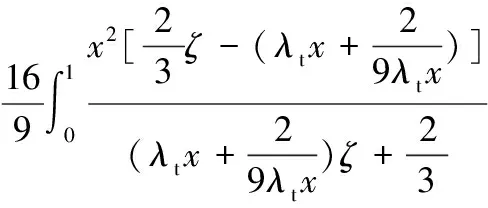
(18)

式(18)比式(16) 的计算值略小一点，但两者的图像十分相似，在尖速比大于4以后这两个图像几乎重合。虽然推导出风力机的最高转矩性能的解析表达式(18)，但未考虑叶尖损失的影响，因此式(18)理论价值较高，实用价值较低。由式(18)直接计算出未考虑叶尖损失的最高转矩系数的理论值，并与表2的数值计算结果进行比较，计算分析表明，对于尖速比在4～10、升阻比在100以下的实用范围内的叶片，叶尖损失导致转矩性能损失均在10%以内，且具体数值随尖速比变化较大，而随升阻比的变化极小。

实际上，式(17) 和表2已给出叶尖损失修正后与升阻比和尖速比关联的最高转矩性能和具体参数值，可作为设计风力机转矩性能最实际的追求目标，因此兼具重要的理论与应用价值。

4 结论

(1)由叶素-动量理论可导出考虑叶尖损失的弦长公式，叶尖损失对弦长的影响主要集中在叶尖部位。

(2)转矩沿翼展积分可导出考虑叶尖损失的最高转矩性能计算公式，这是实际风力机转矩系数的最高值。

(3)不考虑阻力影响的情况下，尖速比从10变化到4时，叶尖损失导致转矩性能损失约4%～10%。

(4)对于尖速比在4～10、升阻比在100以下的实用范围内，叶尖损失导致转矩性能损失在10%以内，且随尖速比变化较大，而随升阻比的变化极小。

[1] BETZ A. Das Maximum der Theoretisch Möglichen Ausnützung des Windes durch Windmotoren[J]. Zeitschrift für das Gesamte Turbinewesen,1920, 20: 307-309.

[2] BERGEY K H. The Lanchester-Betz limit[J]. Journal of Energy, 1979,3: 382-384.

[3] van KUIK G A M. The Lanchester-Betz-Joukowsky Limit[J]. Wind Energy, 2007(10): 289-291.

[4] 姜海波,曹树良,阳平.水平轴风力机的功率极限[J].机械工程学报, 2011, 47 (10): 113-118. JIANG Haibo, CAO Shuliang, YANG Ping. Power Limit of Horizontal Axis Wind Turbine[J]. Chinese Journal of Mechanical Engineering, 2011, 47 (10): 113-118.

[5] PRANDTL L, TIETJENS O G. Applied Hydro and Aeromechanics[M]. New York: Dover Publications, 1957.

[6] TONY B, DAVID S, NICK J, et al. Wind Energy Handbook[M]. Hoboken: John Wiley & Sons Ltd.,2005.

[7] 马丁·汉森. 风力机空气动力学[M].2版.北京: 中国电力出版社,2009. MARTIN O L H. Aerodynamics of Wind Turbines[M]. 2nd ed. Beijing: China Electric Power Press, 2009.

[8] 贺德馨. 风工程与工业空气动力学[M]. 北京: 国防工业出版社, 2006: 81-185. HE Dexin. Wind Engineering and Industrial Aerodynamics[M]. Beijing:National Defense Industry Press, 2006: 81-185.

[9] JIANG Haibo, LI Yanru, CHENG Zhongqing. Performances of Ideal Wind Turbine[J]. Renewable Energy, 2015, 83(11) : 658-662.

(编辑胡佳慧)

TorquePerformanceofHorizontalAxisWindTurbinesandItsImpactsofBladeTipLosses

JIANG Haibo LI Yanru ZHAO Yunpeng
Logistics College,Naval University of Engineering,Tianjin，300450

This paper analyzed the mechanism of blade tip losses, and derived the blade chord formula according to PRANDTL and GLAUERT blade tip loss correction factor and blade element-momentum theory. With the blade chord formula, an analytical expression of torque coefficient associated with tip speed ratio and airfoil lift drag ratio of wind turbines was deduced by integrating along the wingspan using the blade element-momentum theory, and highest torque coefficient value of wind turbines in any steady state was obtained, which might be used for pre-estimating torque coefficient of actual wind turbines in design. The research shows, the impacts of blade tip losses to chord concentrated in the blade tip area, blade tip loss will reduce the torque coefficient about 4 to 10 percent when tip speed ratio changes from 10 to 4, and the value of the loss has minimal changes with lift drag ratio.

wind energy utilization; wind turbine; torque coefficient; blade tip loss; blade element-momentum theory

TK89

10.3969/j.issn.1004-132X.2017.18.009

2016-11-14

国家自然科学基金资助项目(51375489)

姜海波，男，1962年生。海军工程大学勤务学院教授、博士研究生导师。主要研究方向为可再生能源开发利用。获国家科技进步一等奖1项。出版专著1部，发表论文30余篇。E-mail：jianghaibo022@126.com。李艳茹，女，1974年生。海军工程大学勤务学院副教授、博士。赵云鹏，男，1974年生。海军工程大学勤务学院副教授。