渐开线花键副微动磨损分析的能量耗散法

郑维彤 王三民 颉晓欣 李 浩

西北工业大学机电学院，西安，710072

渐开线花键副微动磨损分析的能量耗散法

郑维彤 王三民 颉晓欣 李 浩

西北工业大学机电学院，西安，710072

针对航空传动系统中的渐开线花键副，采用能量耗散法，建立了微动磨损量计算公式，并针对三种工况，研究工况因素对磨损分布规律的影响。研究结果表明:①理想工况下，各齿对的磨损量几乎相同，外花键齿廓上齿根接触末端为最大磨损发生位置；存在侧隙时，侧隙越小的齿间磨损越严重；存在轴线偏斜时，齿面在轴向位置的中部发生较大磨损，最大磨损发生位置向齿顶移动。②渐开线花键副设计安装时，为减少微动磨损带来的失效，应尽可能保证各齿间侧隙均匀并减小内外花键的轴线偏斜。

渐开线花键副；能量耗散法；微动磨损；有限元分析二次开发；磨损分布

0 引言

渐开线花键副具有受载均匀、承载能力大、导向性好等优点，故在工程中得到广泛应用。航空动力传动中，渐开线花键副的工况恶劣，易出现不均匀侧隙和轴线偏斜等状况，使得花键接触齿面磨损严重，进而导致连接失效。

振动的存在，使得看似“相对静止”的内外花键接触面之间仍存在微动磨损。微动磨损不仅会导致花键表面磨损，产生磨屑，引起配合面咬合、松动，也会加速裂纹萌生、扩展，使构件的使用寿命大大降低。渐开线花键副为紧配合部件，内外花键之间产生的滑移非常小，属于微动磨损[1]。

对微动磨损量的仿真计算一般采用经典Archard模型法，而利用该方法进行磨损仿真时，因忽略摩擦因数在振动中的变化，因而其磨损计算的误差较大。

近年来，国外学者提出了一种根据物体相对滑移时产生的能量耗散来计算微动磨损量的能量耗散法，并进行了大量研究。MATVEEVSKY等[2]的研究表明，摩擦功率强度(单位面积消耗的摩擦能)与研究油润滑的赫兹点和线接触时的磨损量有关。SAUGER等[3]、FOUVRY等[4]定义了一个可以将磨损体积的演变与磨损过程中消耗的额外能量联系起来的能量磨损系数。ZHANG等[5]提出一种基于能量法的有限元分析方法，用来比较相同法向载荷、位移和边界条件下不同接触几何体之间的差异。BASSEVILLE等[6]对常用的两平面接触磨损模型进行改进，在接触表面中引入颗粒作为磨损碎屑以预测微动疲劳中的初始裂纹。

在国内，能量耗散法在磨损方面的研究也取得了一些成果。顾家威等[7]从能量角度分析了激光熔覆涂层，发现累积耗散能主要用于磨屑的产生，且磨屑量与输入能量正相关。李斌[8]对磨损表面显微结构进行研究，推导出基于能量耗散的低周疲劳寿命预测模型。在微动磨损动态仿真领域，刘峰璧[9]基于Archard磨耗方程，结合赫兹接触理论，采用数值方法对直齿圆柱齿轮磨损过程进行了模拟计算。潘尔顺等[10]将边界元思想用于微动磨损分析，对齿轮边界曲线上的离散节点进行动态啮合分析与磨损量计算，并用三次参数样条曲线模拟主从动齿轮磨损后的齿面轮廓。

本文将能量耗散法用于渐开线花键副的磨损分析中，针对典型的渐开线花键连接形式，设计三种不同工况，对于每一种工况，采用Abaqus-Python-MATLAB的有限元二次开发方法，获得航空渐开线花键副的剪切应力和相对滑移速率，并利用能量耗散模型计算微动磨损量，通过对计算结果进行处理，找到齿面磨损量分布规律，为渐开线花键副的设计及磨损量预估提供参考。

1 渐开线花键副接触模型

1.1几何模型

外花键为主动件，内花键为从动件，渐开线花键副参数如表1所示。

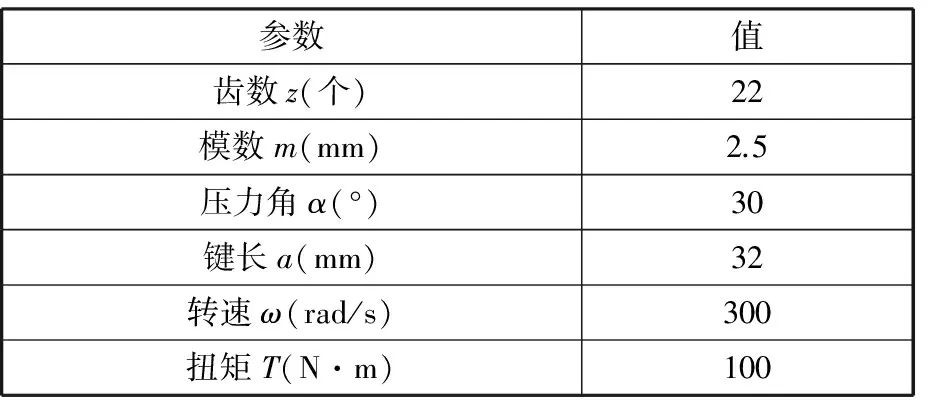
表1 渐开线花键参数

本文研究的花键模型选用定心精度高、定心稳定性好的小径定心方式进行装配。

1.2有限元网格模型

本研究选用C3D8R线性缩减积分单元作为六面体网格单元。内花键共计85 080个六面体单元，外花键共计113 940个六面体单元。有限元网格模型及外花键齿编号如图1所示。

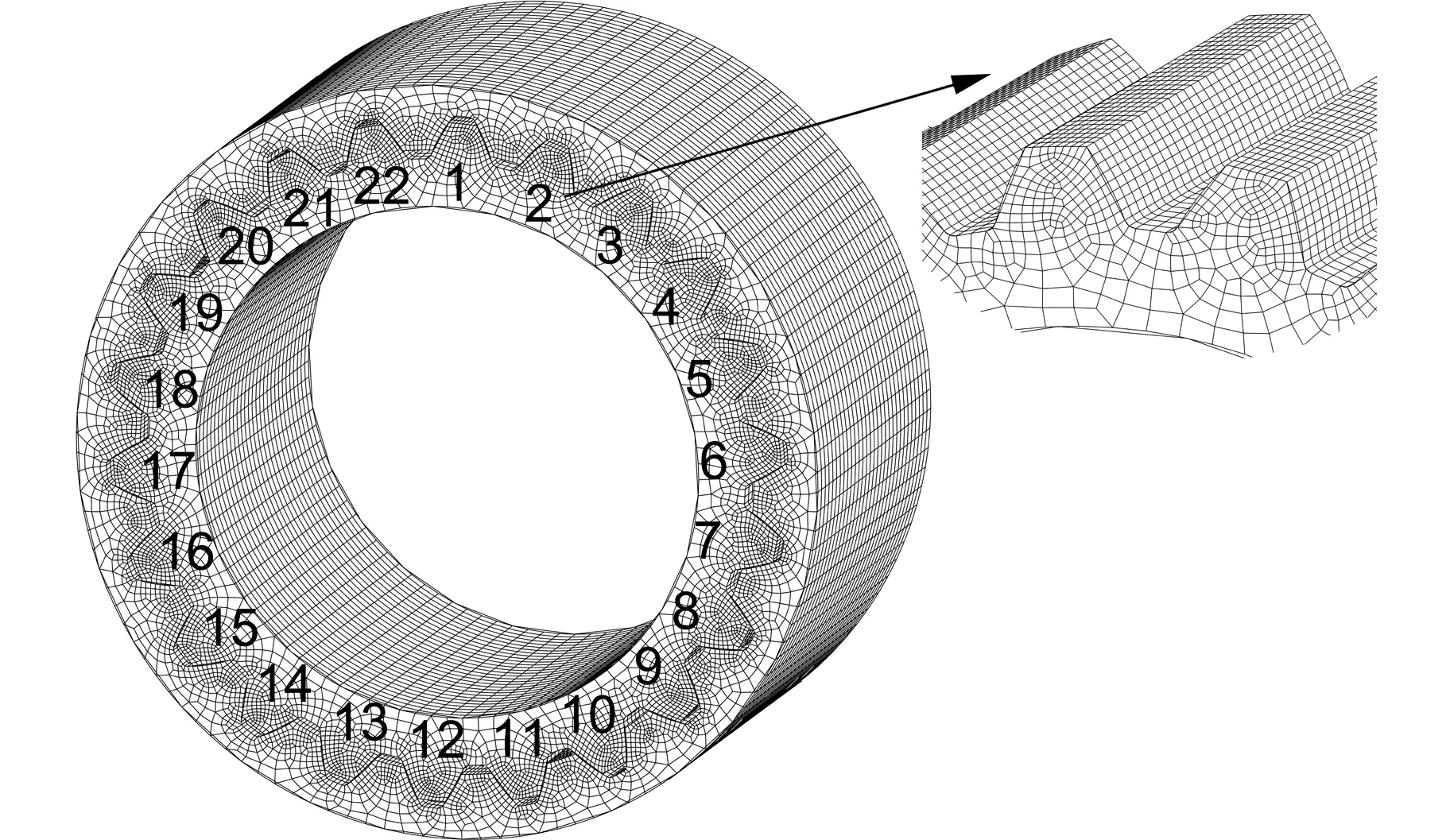
图1 有限元网格模型及外花键齿编号Fig.1 Finite element model and number of external spline tooth

1.3边界条件与接触设置

1.3.1边界条件

本文主要针对花键副的动态啮合问题进行研究，外花键提供的正向恒定转速为300 rad/s，内花键提供的反向恒定负载扭矩为100 N·m，内外花键均只保留绕z轴转动的自由度。

1.3.2接触设置

Abaqus/Explicit求解器提供接触对算法和通用接触算法来模拟接触问题[11]，通用接触算法中对接触面限制较少，故选用接触设置更为精细的接触对算法中的罚函数接触来模拟花键副动态啮合接触。

2 微动磨损计算

2.1磨损模型

以往的渐开线花键副磨损计算中，经常采用的是Archard模型，但Archard模型适用于两接触物体间具有明显相对位移的情况，不能准确计算渐开线花键副内外花键间发生的部分黏着、部分滑移的微动磨损，且Archard模型由于其自身的限制，不能对变摩擦因数接触进行精确的分析。

相对于Archard模型，能量耗散法的优势是磨损系数不会随位移幅度的变化而变化，并可通过若干参数来确定微动区域[12]。

微动条件下，相对运动存在两种情况：①部分滑移，即接触中心黏着而接触边缘存在微滑；②完全滑移，即两接触体各点之间均发生相对滑移。

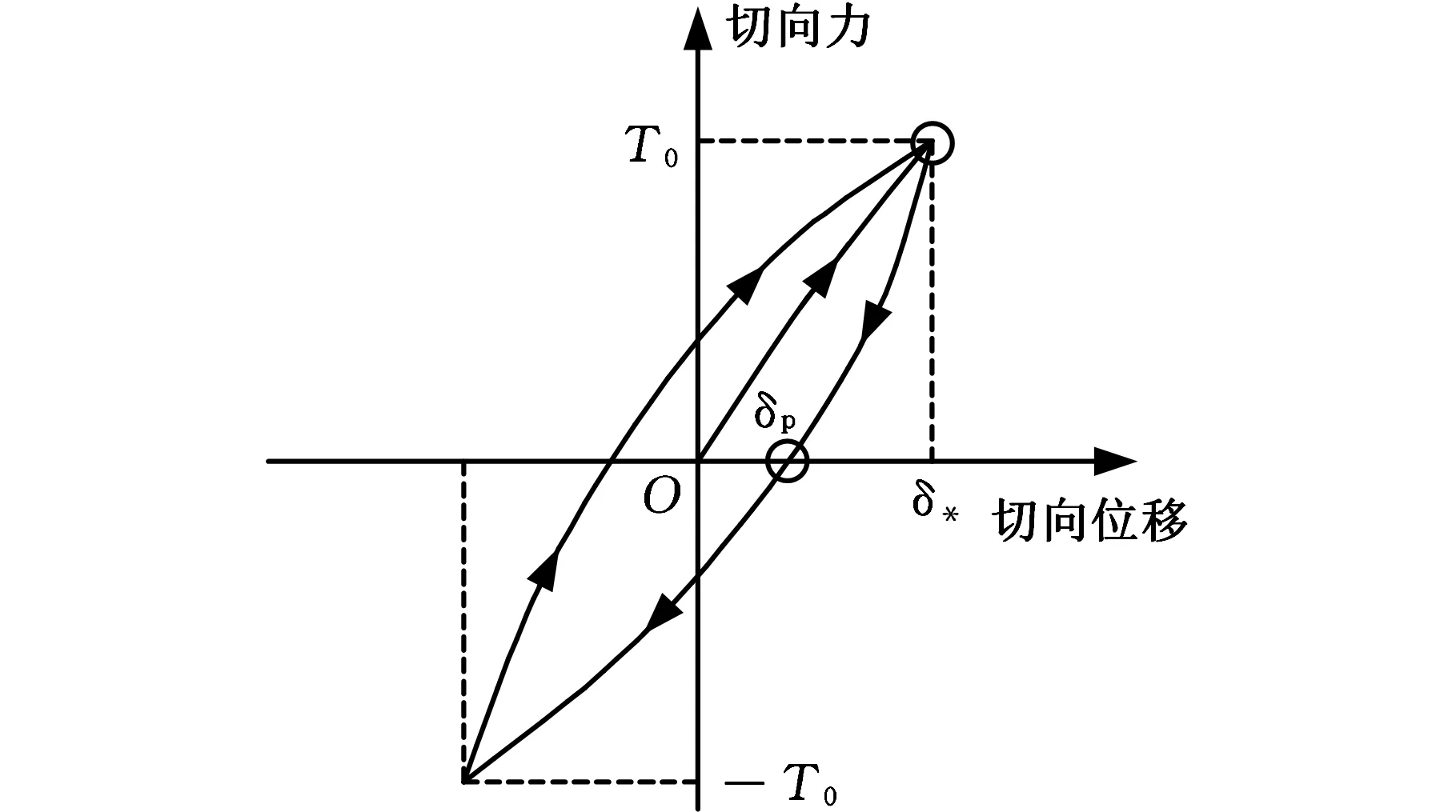
图2 切向力与切向位移关系示意图Fig.2 Relationship diagram of tangential force and tangential displacement

图2为外加激振力作用下切向力和切向位移的关系示意图。切向力很小时，微动表面产生的微滑由弹性变形协调，图中位移与切向力成线性关系；切向力较大时，接触区的微滑伴随着材料的弹塑性变形，图像呈类似椭圆状，椭圆形区域所包含的部分的面积即为部分滑移状态下微动循环的耗散能量，表示为Ed。

FOUVRY等[13]引入3个与切向力-位移曲线相关的能量参数A、B、C来定量描述微动的相对运动由部分位移向完全位移转变的过程：

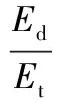
式中，A为能量比；B为滑动比；C为非系统依赖转变判据；Ed为微动循环的耗散能；Et为系统全部能量；E0为循环滞后能量；δp为微动循环滞后位移；δ*为滑动位移。

FOUVRY等[13]同时给出了部分滑移向完全滑移转变的临界条件：A=0.2，B=0.26，C=0.77。

RAMALHO等[14]通过实验对能量耗散法与Archard模型法在微动磨损量计算的准确性上进行了对比。他们将两交叉圆柱体磨损实验的实验结果分别同两种方法的磨损预测值进行磨损量-转数曲线拟合，发现三种不同材料情况下，能量耗散法相比于Archard模型法均具有较高的线性相关性，实验结果证明了能量耗散法的精度高于Archard模型法。

虽然在微动磨损分析中，能量耗散法相对于Archard模型法有着更高的精度，但是由于微动循环耗散能Ed的准确测量需要仪器具有较高的参量率和测量精度，所以能量耗散法并没有得到普遍使用。

能量耗散方程假设磨损是因摩擦而失去的能量的线性函数[15]，微动磨损体积V与每个周期耗散能量Edi的关系为

(1)

式中，λ为所研究的接触相互作用在给定滑动幅度下的能量磨损系数；N为微动磨损的总周期数。

能量耗散方程可以取滑动距离增量dx，并在一个小的面积为dS的线性接触区域进行微分运算，即

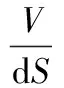
(2)

式中，Ft为由于摩擦产生的切向力。

用剪切应力τ代替Ft/dS，即有

dh=λτdx

(3)

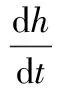
(4)

(5)

式(5)等号两侧对时间积分：

(6)

h即为通过能量耗散法求出的在此微小区域的磨损深度。

2.2基于Python的Abaqus二次开发

Abaqus求解结束后生成odb结果文件，使用Python脚本访问结果数据库，实现对结果文件的读写；使用xyDataListFromField函数读取odb文件中的场变量数据来生成XYData对象；再使用writeXYReport函数将XYData写入文本文件，为接下来的MATLAB读取数据作准备。花键磨损有限元计算流程如图3所示。

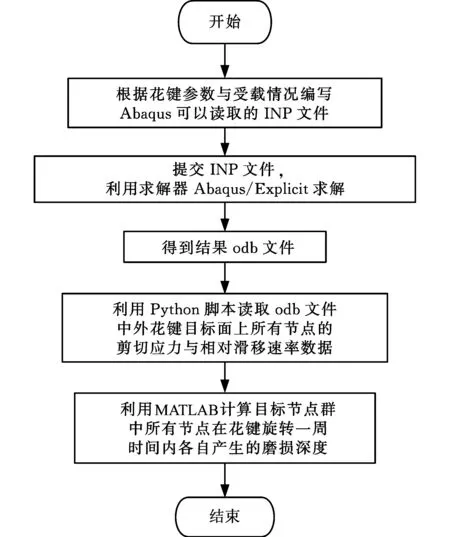
图3 花键磨损有限元计算流程图Fig.3 Flow chart of finite element calculation for spline wear

3 结果与分析

为研究渐开线花键副在不同工况下的磨损深度分布规律，设定三种工况条件，如表2所示。

表2 渐开线花键副工况表

为与其他两种工况下的微动磨损情况进行比较，将工况一设定为理想工况。工况二中，花键齿间最小侧隙为0，最大侧隙为20 μm，为便于找出各齿面总磨损量与齿间侧隙的规律，将1号齿侧隙设置为0，22号齿侧隙设置为20 μm，其间20对齿的侧隙按等差数列规律由小到大设置。

工况三中，将花键以点(0,0,16 mm)为旋转中心，平行yz平面旋转0.3°,完成模型的建立。

工况三中设定内外花键轴线间存在0.3°的偏斜角，旋转中心为外花键模型的几何中心点。工况三外花键轴偏斜情况如图4所示。

图4 工况三中外花键轴偏移角示意图Fig.4 Schematic diagram of the deflection angle of the external spline shaft in working condition three

3.1工况一

选取18号齿为对象，分析工况一条件下齿面磨损分布规律。接触齿面为齿在转动方向上与内花键齿相接触的一侧齿面，其上有10个齿高位置与31个轴向位置，每个轴向位置存在一条齿廓渐开线，如图5所示。

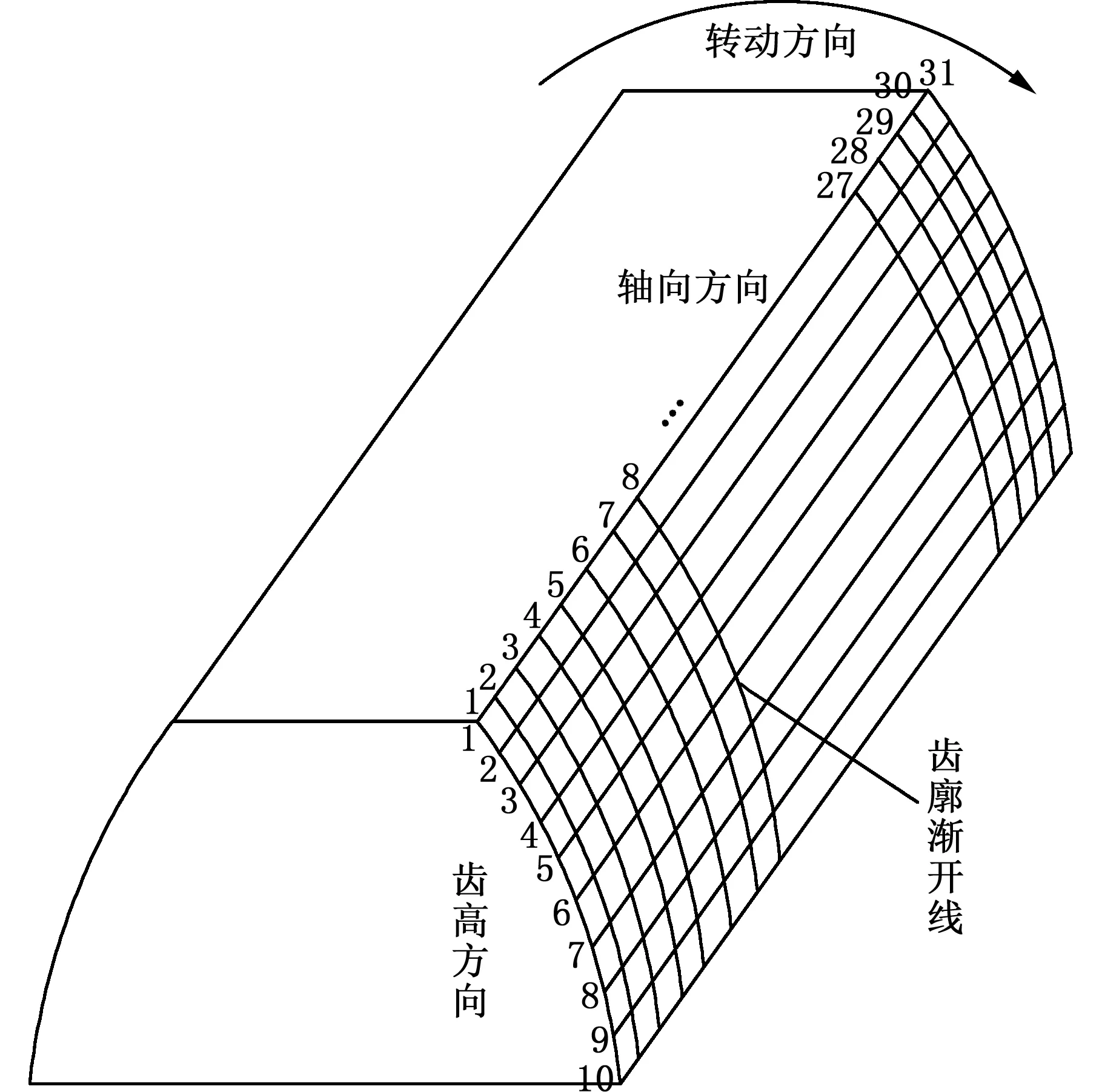
图5 接触齿面各参数命名示意图Fig.5 Naming diagram of the parameters of the contact tooth surface

3.1.1齿高位置的影响

图6 理想工况下磨损量沿齿高位置的分布情况 Fig.6 Distribution of wear along the tooth position under ideal working condition

外花键的齿廓为渐开线，不同的齿高位置有不同的受力状况，进而导致不同的磨损程度。选取编号为8、15、25的三条齿廓渐开线作为研究对象，其磨损量曲线如图6所示。由图6可以看出，在齿高位置1、2、3处磨损量基本保持稳定，在齿高位置4、5处呈下降趋势，在齿高位置6、7处上升并在7处取得三条渐开线各自的最大磨损量，由此可知在渐开线齿廓上，7处为发生磨损最为严重的位置；在齿高位置8、9、10处磨损量均为0，此三处为底隙所在位置，不与内花键接触，故未发生磨损。

3.1.2轴向位置的影响

选取齿高位置2、5、7，绘制三个位置沿轴向方向的磨损量分布图(图7)。

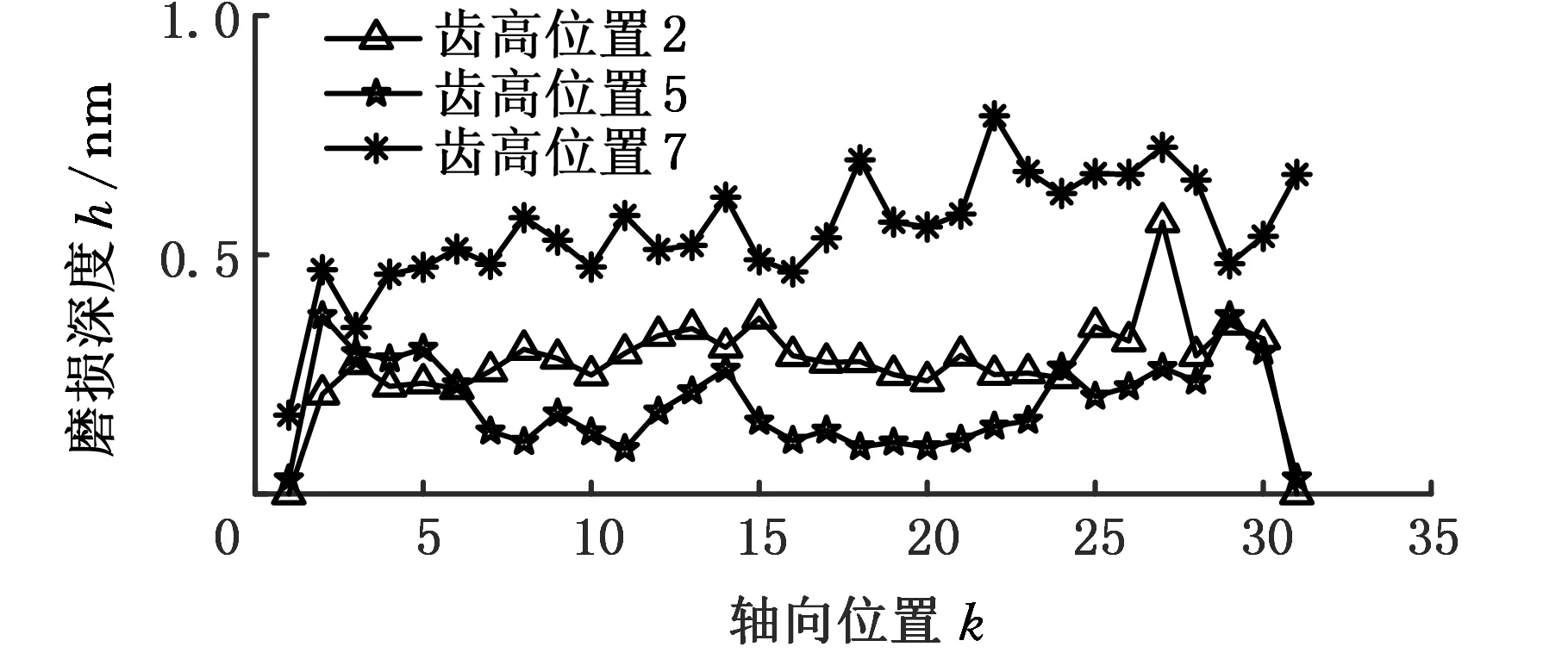
图7 理想工况下磨损量沿轴向位置的分布情况Fig.7 Distribution of wear along the axial direction under ideal condition

由图7可以看出，磨损分布沿轴向分布基本保持稳定，轴两端产生的磨损量较小，是由于轴端节点所处单元仅有一侧与其他单元相互作用所导致的；齿高位置7的整体磨损量较大，齿高位置5的整体磨损量较小，符合前文所得出的在齿高位置7处取得渐开线齿廓最大磨损量的结论。

3.2工况二

工况一与工况二下的各齿面总磨损量分布情况如图8所示。由图8可知，侧隙均匀的工况一条件下，由于受载均匀，故各齿面总磨损量分布较为平均；在齿间侧隙逐渐增大的工况二条件下，各齿面总磨损量随侧隙增大而减小；由于各齿受载不均匀，最先接触受载的1号齿磨损最为严重，齿面总磨损量约为其均匀受载时的2倍。由侧隙为18.095 μm的20号齿开始，20、21、22号齿由于侧隙过大而未发生接触，故齿面未发生磨损。

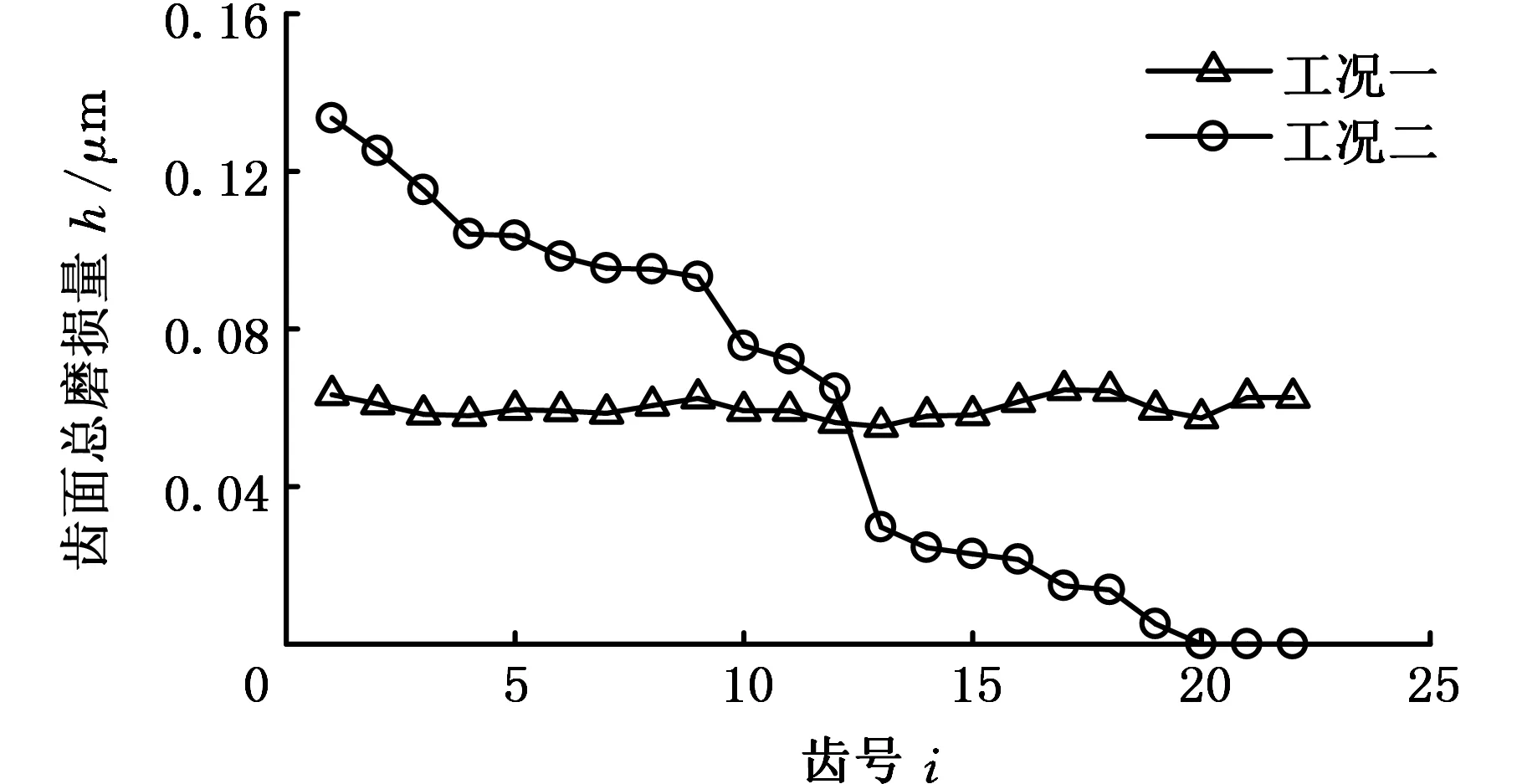
图8 工况一与工况二下各齿面总磨损量分布情况Fig.8 Distribution of total wear of each tooth surface in working condition one and working condition two

3.3工况三

工况三情况下，选择受轴线偏斜影响最大的8号齿进行研究，选取齿高位置2、5、7，绘制三个位置沿轴向方向的磨损量分布图(图9)。

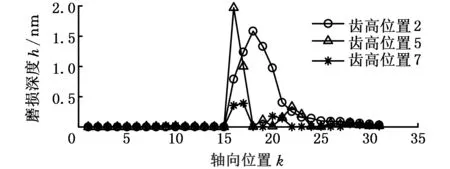
图9 轴线偏斜工况下磨损量沿轴向位置的分布情况Fig.9 Distri bution of wear along the axial position under axial deflection condition

由图9可以看出：轴向位置方面，由于内外花键存在0.3°的轴线偏斜，故导致外花键两端几乎未与内花键发生接触，轴向位置的中间部分发生较大磨损；齿高位置方面，轴线偏斜的存在致使外花键齿面接触区域向齿顶移动，同时使最大磨损发生位置由理想条件下的齿高位置7向齿顶位置移动。根据此结论，即可解释相关文献中航空发动机花键上的微动疲劳裂纹的产生位置及原因，为工程中防止此类失效的发生提供参考。

4 结论

(1)理想工况下，各齿由于受载均匀，总磨损量几乎相同，外花键渐开线齿廓上齿根接触末端为最大磨损发生位置；存在侧隙时，各齿受载情况由侧隙大小决定，侧隙越小的齿间磨损越严重，磨损最严重的1号齿的总磨损量约为理想工况下总磨损量的2.25倍；存在轴线偏斜时，齿面在轴向位置的中部接触，轴向位置两端未发生接触，从而未产生磨损，最大磨损发生位置向齿顶移动，最大磨损量约为理想工况下的2.5倍。

(2)不均匀侧隙与轴线偏斜会加重齿面微动磨损，渐开线花键副安装时，应使各齿间侧隙均匀并减小内外花键的轴线偏斜。

[1] 周仲荣, 朱旻昊. 复合微动磨损[M]. 上海:上海交通大学出版社, 2004：11-13 ZHOU Zhongrong, ZHU Minhao.Composite Fretting Wear[M]. Shanghai: Shanghai Jiao Tong University Press, 2004:11-13.

[2] MATVEEVSKY R M. The Critical Temperature of Oil with Point and Line Contact Machines[J]. Journal of Basic Engineering, 1965, 87(3): 754-759.

[3] SAUGER E, FOUVRY S, PONSONNET L, et al. Tribologically Transformed Structure in Fretting[J]. Wear, 2000, 245(1): 39-52.

[4] FOUVRY S, KAPSA P, VINCENT L. An Elastic-plastic Shakedown Analysis of Fretting Wear[J]. Wear, 2001, 247(1): 41-54.

[5] ZHANG T, MCHUGH P E, LEEN S B. Computational Study on the Effect of Contact Geometry on Fretting Behaviour[J]. Wear, 2011, 271(9): 1462-1480.

[6] BASSEVILLE S, HÉRIPRÉ E, CAILLETAUD G. Numerical Simulation of the Third Body in Fretting Problems[J]. Wear, 2011, 270(11): 876-887.

[7] 顾家威, 李强强, 冯盛, 等. 基于累积能量耗散法的涂层磨损行为的研究[J]. 应用激光,2015,(6):643-647. GU Jiawei, LI Qiangqiang, FENG Sheng, et al. The Study of Wear Behavior of the Coating Based on the Accumulated Dissipated Energy[J]. Applied Laser, 2015,(6):643-647.

[8] 李斌. 基于能量耗散的金属疲劳损伤表征及寿命预测[D].西安：西北工业大学,2014. LI Bin. Study on the Low-cycle Fatigue Damage Characterization and Life Prediction of Metals Based on the Energy Dissipation Theory[D]. Xi’an: Northwestern Polytechnical University, 2014.

[9] 刘峰璧. 直齿圆柱齿轮磨损过程模拟[J].机械科学与技术,2004,23(1):55-56. LIU Fengbi. Simulation of Wear Process in Spur Gear[J]. Mechanical Science and Technology, 2004,23(1):55-56.

[10] 潘尔顺, 王殊轶. 渐开线圆柱齿轮啮合过程中磨损的计算机仿真[J].上海交通大学学报,2000,34(3):415-418. PAN Ershun, WANG Shuyi. Computer Simulation of Wear in Meshing Process of Involute Cylindrical Gear[J]. Journal of Shanghai Jiaotong University, 2000,34(3):415-418.

[11] 宋子林. 变速器渐开线花键磨损仿真分析[D]. 广州：华南理工大学, 2014. SONG Zilin, Finite Element Simulation of Transmission Involute Spline Wear[D]. Guangzhou: South China University of Technology, 2004.

[12] MCCOLL I R, DING J, LEEN S B. Finite Element Simulation and Experimental Validation of Fretting Wear[J]. Wear, 2004, 256(11): 1114-1127.

[13] FOUVRY S, KAPSA P, VINCENT L. Quantification of Fretting Damage[J]. Wear, 1996, 200(1/2):186-205.

[14] RAMALHO A, MIRANDA J C. The Relationship between Wear and Dissipated Energy in Sliding Systems[J]. Wear, 2006, 260(4): 361-367.

[15] YUE T, WAHAB M A. Finite Element Analysis of Stress Singularity in Partial Slip and Gross Sliding Regimes in Fretting Wear[J]. Wear, 2014, 321(1): 53-63.

(编辑胡佳慧)

DissipatedEnergyMethodforFrettingWearAnalysisofInvoluteSplines

ZHENG Weitong WANG Sanmin XIE Xiaoxin LI Hao
School of Mechanical Engineering，Northwestern Polytechnical University,Xi’an,710072

Aiming at involute spline pairs in aerial drive systems，with dissipated energy method，calculation formula for fretting wear amount was established. Besides, for three working conditions, the effects of working conditions on the distribution characteristics were studied. Consequently the conclusions were obtained as follows. Under ideal working conditions, the wear of each tooth is nearly the same, and root contact end on external spline tooth profile acts as the maximum wear position. When there is a lateral gap, the smaller the side gap is, the more serious the wear between the teeth is. When the axial deflection occurs, the wear is more serious in the middle part of the tooth surfaces in the axial position, and the maximum wear position moves towards the top of the tooth. In the design and installation of involute spline pair, to reduce failure caused by fretting wear, it is required to keep the tooth gap between the teeth evenly as far as possible. And the reduction is also suggested for the axis deviation of internal and external splines.

involute spline pair; dissipated energy method; fretting wear; secondary development of finite element analysis; wear distribution

2016-11-23

航空推进技术验证计划(APTD计划)资助项目(KY-44-2013)

V232.9；TH117.1

10.3969/j.issn.1004-132X.2017.18.004

郑维彤，男，1993年生。西北工业大学机电学院硕士研究生。主要研究方向为航空发动机传动。E-mail：65293361@qq.com。王三民，男，1960年生。西北工业大学机电学院教授、博士研究生导师。颉晓欣，男，1992年生。西北工业大学机电学院硕士研究生。李浩，男，1993年生。西北工业大学机电学院硕士研究生。