弧齿锥齿轮高精度离散数值齿面啮合分析

刘光磊，常 凯

（西北工业大学机电学院，西安 710072）

0 引言

弧齿锥齿轮齿面的分为间接法[1-9]和直接法[10-17]。在判断加工参数的合理性时，一般采用基于间接法对齿面进行啮合分析；在检验齿面的啮合性能时，除了已知的滚检机外，采用齿面直接法进行轮齿啮合分析有望成为1个额外的选择。相对于比较成熟的间接法分析，直接法轮齿啮合分析尚在发展和完善中。Zhang Y[10]将理论齿面与误差齿面叠加，采用5元3次非线性方程组间接表示真实齿面，与实际存在较大误差；李左章[11]采用了5元3次非线性方程组，建立求解齿面接触点的目标函数，运用复合形法，使计算过程稳定；孙殿柱、苏智剑和张军辉都采用3次非均匀有理B样条，拟合螺旋锥齿轮齿面测量点。其中，孙殿柱[12]提出了不断减小齿面间距，从而逐步逼近齿面接触点的方法，几何意义清楚；苏智剑[13]提出用齿面计算点的连线与其中1个计算点的法线之间的夹角作为目标函数，并用复合形法求解齿面接触点；张军辉[14]对比了离散数值齿面啮合分析与传统轮齿啮合分析技术；刘光磊[15-17]采用双3次样条拟合理论齿面离散点。上述直接法轮齿啮合分析技术，有一些往往没有给出令人信服的结果，而无法证明其方法的有效性。

本文基于双3次样条法，系统分析弧齿锥齿轮高精度离散数值齿面啮合技术，为评价弧齿锥齿轮真实齿面的啮合质量以及弧齿锥齿轮加工参数反求和齿面重构提供手段和理论依据。

1 基本坐标变换

1.1 齿面3坐标测量数据描述

采用3坐标测量机测量齿面时，得到9×5个点，虚线交点如图1所示。其中，齿长方向9个，齿高方向5个，全部位于齿面边界之内。测量坐标系的原点位于锥顶；x轴沿齿轮径向指向齿面；z轴与齿轮轴线重合，从大端指向小端；y轴按右手规则确定，指向齿面离散点的中心点。

图1 齿面离散数据测量区域

1.2 从测量坐标系到加工坐标系

为了便于与加工时的结果相比较，需要将测量的齿面离散点转换到加工时的齿轮坐标系中。在加工时，与齿轮固结的坐标系的原点与锥顶重合；x轴与齿轮轴线重合，从小端指向大端；z轴沿齿轮径向指向齿面；y轴按右手规则确定。

从测量坐标系到加工坐标系的矢量变换为

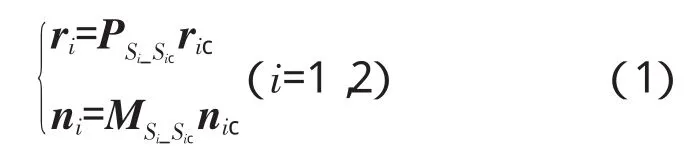
式中：ri和ric、ni和nic分别为加工坐标系Si和测量坐标系Sic中齿面离散点的位置矢量和法线矢量；角标i=1，2，分别表示小轮和大轮；PSi_Sic和 MSi_Sic分别为位置矢量和法向量变换矩阵，即

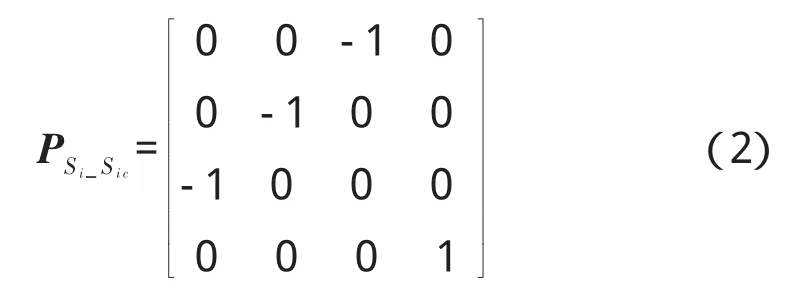
而法线矢量变换矩阵MSi_Sic取PSi_Sic中的前3行和前3列。

1.3 从加工坐标系到啮合坐标系

离散齿面啮合分析在啮合坐标系中进行。令小轮坐标系S1的初始位置S10与啮合坐标系Sh重合，那么，从小轮和大轮加工坐标系到啮合坐标系的变换关系为

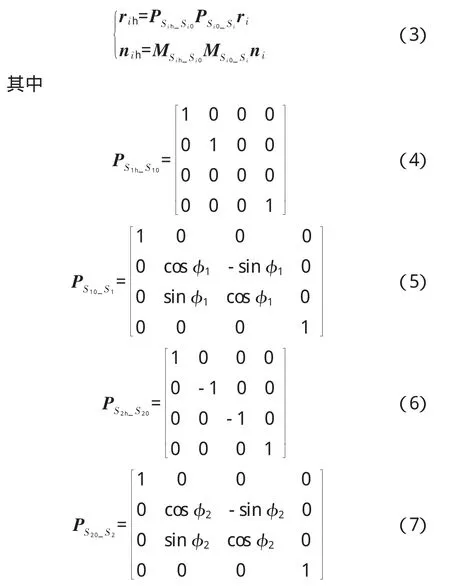
式中：φ1、φ2分别为 Si0与 Si之间的夹角；MSih_Si0、MSi0_Si做法同式（1）。

2 齿面啮合点求解技术

2.1 离散点插值与加密的双3次样条法

测量得到的齿面离散点过于稀疏，需要加密。采用3次样条先沿齿长方向分段光顺，然后在样条曲线上插入离散点；再沿齿高方向用3次样条光顺，同样插入离散点。这种分别沿齿长和齿高方向插值和加密的方法称为双3次样条法[11]。

2.2 齿面间距求解的局部坐标法

为了计算齿面间距，以靠近小端齿顶、小端齿根和大端齿根的3个离散点构建齿面局部坐标系。将小轮和大轮齿面离散点从加工坐标系转换到该坐标系中，从一齿面上的离散点沿该处法线方向作直线，与另一齿面上3个相邻点构成的三角形平面相交。当交点位于三角形内时，与三角形顶点连线之间的夹角之和等于360°，否则，交点位于三角形之外。一般交点不会落在离散点上，为此，用相邻离散点构成的四边形的1个角点来代表求解结果。当离散点间距足够小时，可以将角点看作交点。齿面距离采用有向直线表示。当齿面有间隙时，距离为正；当齿面干涉时，距离为负。

2.3 搜索齿面最小间距的流水法

计算齿面最小间距采用全齿面搜索需要很长时间。为此，当从一齿面发出的直线与另一齿面相交后，即以该点为中心，与包围它的8个相邻离散点一起组成1个包含9个离散点的小网格。分别计算这些点上发出的直线到另一齿面的有向距离，从中找出距离最小的点。当距离最小的点位于小网格的中心时，即停止计算。上述过程称为流水法。

2.4 齿面最小间距调整的无约束优化法

轮齿啮合分析，就是在一齿面保持不动时，让另一齿面靠上去，直到2者相切。当齿面间的最小间距满足预定的收敛条件而接近于零时，即认为找到齿面啮合点，不作齿面法线重合的判断。当齿面网格足够小时，啮合点齿面法线误差可以忽略。在调整齿面间距时，因无法判断齿轮转角需要调整的范围，故采用无约束优化方法，建立齿面最小间距为目标函数，齿轮转角为优化设计变量的优化模型。

2.5 齿面逐级加密

为了保证计算精度，齿面网格需要加密。但采用很密的网格，势必花费很长的时间。为此，先用较粗的网格计算齿面间距最小点；然后以该点为中心，选择与其相邻的若干点，组成1个小齿面；再次采用双3次样条插值和加密，计算齿面最小间距。此过程可以一直进行下去，直到达到满意的计算精度。

3 数值齿面啮合分析

3.1 传动误差曲线与齿面接触印痕

在啮合分析时，小轮转角等距变动，调整大轮转角至小轮齿面与大轮齿面相切，大轮转角的变动量为

式中：φ1、φ2分别为小轮和大轮的当前角位置；φ10、φ20分别为小轮和大轮的初始角位置；z1、z2分别为小轮和大轮的齿数。

按照格里森公司经验，取齿面压限量为0.00635 mm，计算齿面干涉区域，由此获得齿面接触印痕。

3.2 啮合分析流程

综合运用上述数值啮合分析技术，模拟齿轮啮合过程，如图2所示。

4 实例

以某型发动机附件传动中弧齿锥齿轮副的小轮凹面和大轮凸面为例，采用Matlab编程，进行离散数值齿面啮合的具体应用分析。

齿轮副基本参数见表1。

经三坐标测量仪得到齿面离散点数据。齿面测量点数据和光顺后的结果如图3所示。齿长方向结点最大间距0.831mm，齿高方向结点最大间距0.591mm。

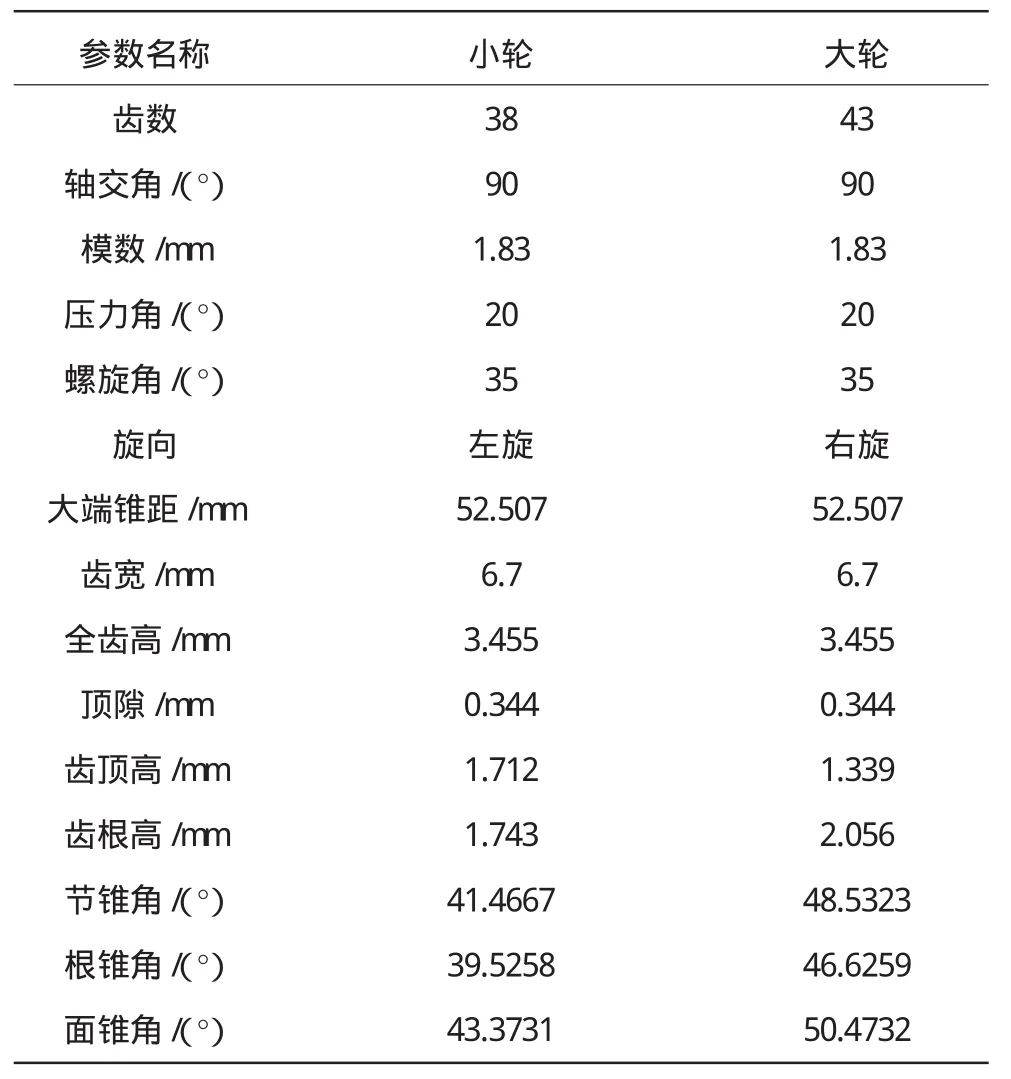
表1 齿轮副基本参数

将图3中的数据经式（1）和式（2）变换至啮合坐标系中，如图4所示。其中，图4（a）为加密前齿面副；图4（b）为齿面网格加密后尚未接触；图4（c）为小轮不动、大轮齿面与小轮齿面刚刚接触。

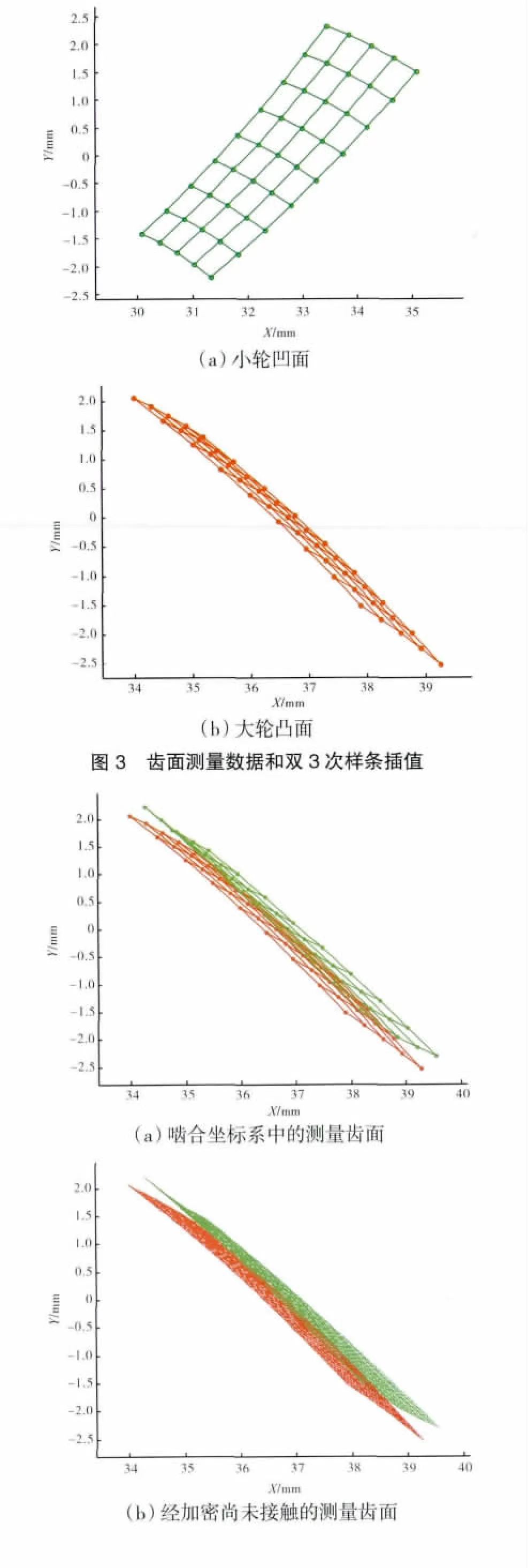
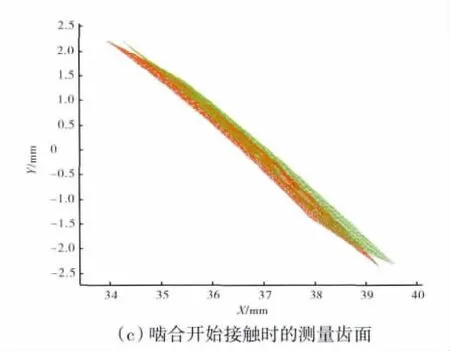
图4 啮合坐标系中的齿面副

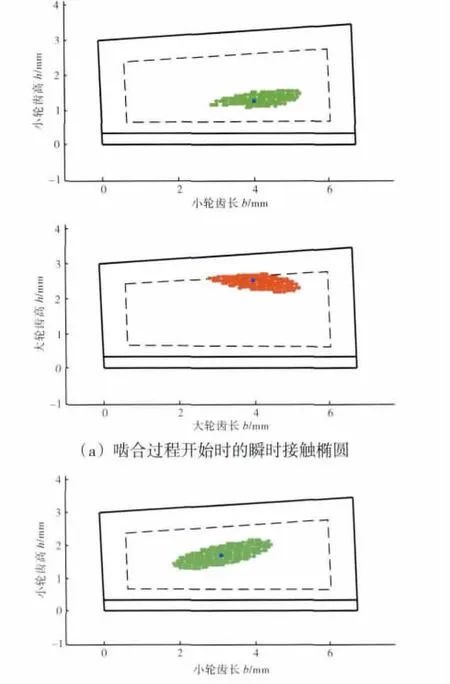
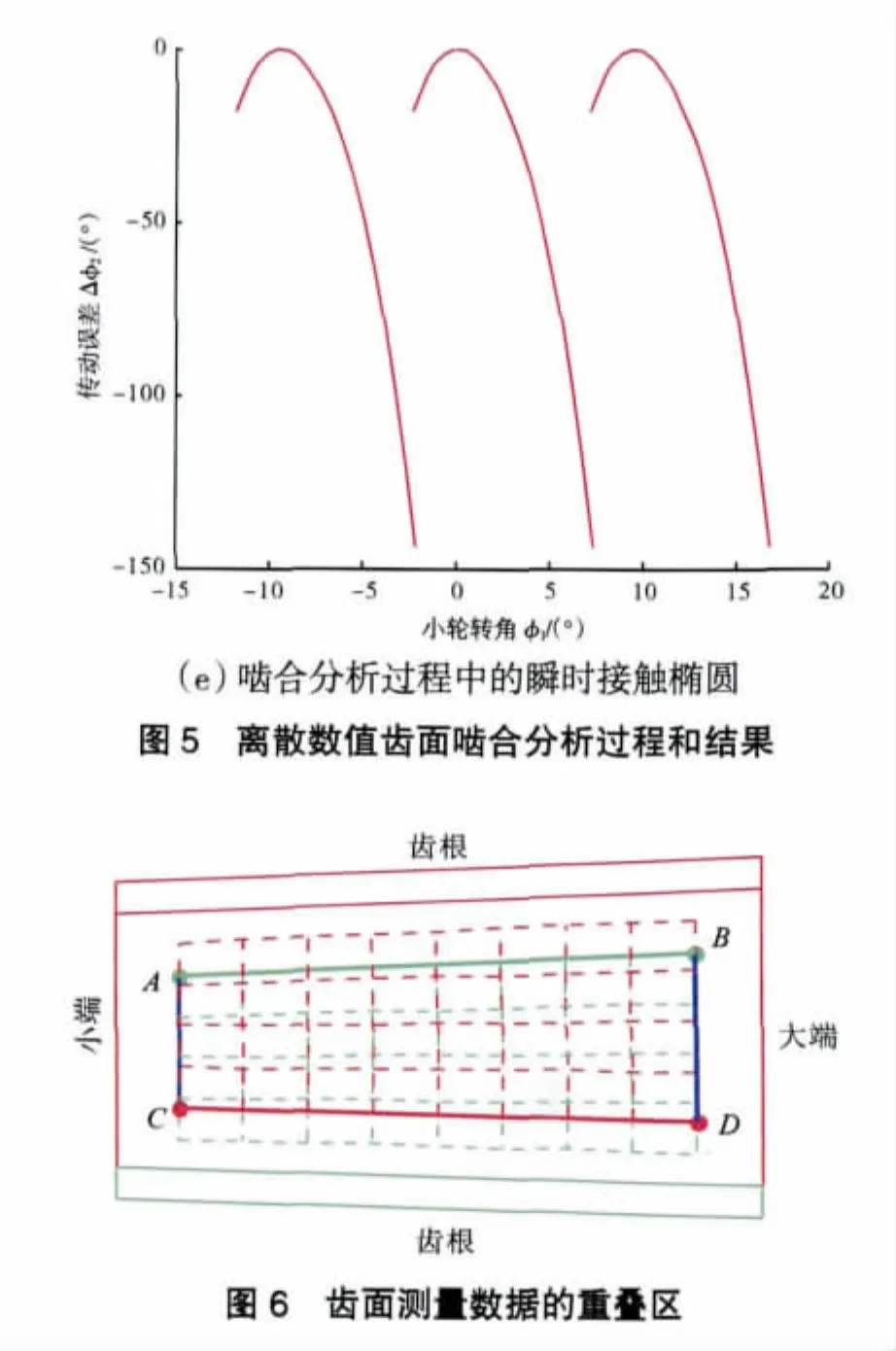
数值齿面轮齿啮合分析过程和结果如图5所示。图 5中（a）、（b）、（c）为啮合分析开始、中间和结束的瞬时接触区，其中的虚线部分为测量数据的边界；图5（d）为单齿啮合的接触印痕；图5（e）为相邻3对齿的传动误差曲线。因齿面测量数据限于齿面边界内，在旋转轴截面内，测量数据只有部分重合，如图6中四边形ABCD所示，所以相邻传动误差曲线没有相交，也无法得到多齿啮合的接触印痕。

5 结论

（1）提出基于3坐标齿面测量数据的弧齿锥齿轮离散数值齿面啮合分析的一系列方法，经对航空弧齿锥齿轮的啮合分析，证明了这些方法的有效性。

（2）为了获得光滑的齿面接触迹和传动误差曲线，网格间距的最大值不应大于0.01mm，啮合分析时的小轮转角步进量不应大于0.01 rad。

（3）由于3坐标测量齿面测量数据比实际齿面要小，基于此的啮合分析一般无法获得完整传动误差曲线和啮合印痕。为了全面评价真实齿面的啮合性能，需要以齿面测量数据为基础，反求真实齿面加工参数，重构和拓展齿面，并经轮齿啮合分析，再现完整的啮合性能。

[1]Gleason Works.Understanding tooth contactanalysis[M].New York：University of Rochester Press,1981：58-71.

[2]Litvin F L.Gear geometry and applied theory[M].New Jersey：Prentice Hall PTR,1994:107-281.

[3]Litvin F L,Wang A G,Handschuh R F.Computerized generation and simulation of meshing and contact of spiral bevel gears with improved geometry[J].Computer Methods in Applied Mechanics and Engineering,1998,158（1-2）:35-64.

[4]Sheveleva G I,Volkov A E,Medyedev V I.Algorithms for analysis of meshing and contact of spiral bevel gear[J].Mechanism and Machine Theory,2007,42（2）:198-215.

[5]郑昌启.弧齿锥齿轮及准双曲面齿轮[M].北京:机械工业出版社,1988：312-373.

ZHENG Changqi.Spiral bevel gears and hypoid gears[M].Beijing:Mechanical Industry Press,1988:312-373.(in Chinese)

[6]曾韬.螺旋锥齿轮设计与加工[M].哈尔滨:哈尔滨工业大学出版社,1989：237-259.

ZENG Tao.Design and manufacture for spiral bevel gears[M].Harbin：Harbin Institute of Technology Press,1989:237-259.(in Chinese)

[7]方宗德,刘涛,邓效忠.基于传动误差设计的弧齿锥齿轮啮合分析[J].航空学报,2002,23（3）:226-230.

FANG Zongde,LIU Tao,DENG Xiaozhong.Tooth contact analysis of spiral bevel gears based on design of transmission[J].Acta Aeronautica et Astronautica Sinica,2002,23（3）:226-230.(in Chinese)

[8]曹雪梅,方宗德,张金良，等.弧齿锥齿轮的齿面主动设计[J].机械工程学报,2007,43（8）：155-158,164.

CAO Xuemei,FANG Zongde,ZHANG Jinliang,et al.Function-oriented active tooth surface design of spiral bevel gears[J].Chinese Journal of Mechanical Engineering,2007,43（8）:155-158,164.(in Chinese)

[9]曹雪梅,方宗德,许浩，等.弧齿锥齿轮的齿面主动设计及试验验证[J].机械工程学报,2008,44（7）:209-214.

CAO Xuemei,FANG Zongde,XU Hao,et al.Function-oriented active tooth surface design of spiral bevel gears and experimental tests[J].Chinese Journal of Mechanical Engineering,2008.44（7）:209-214.(in Chinese)

[10]Zhang Y.Computerized analysis of meshing and contact of gear real tooth surfaces[J].Journal of Mechanical Design,1994,116（1）:677－682.

[11]李左章,王延忠,周云飞,等.螺旋锥齿轮拟合齿面接触点求解算法研究 [J].华中理工大学学报.2000,28（6）:101-103.

LIZuozhang,WANG Yanzhong,ZHOU Yunfei,et al.Getting contacting points of bevel gear tooth fitting surfaces[J].Journal of Huazhong University of Science and Technology,2000,28（6）：101-103.(in Chinese)

[12]孙殿柱,董学朱.真实齿面啮合分析 [J].机械工程学报,2000,36（8）:98-100.

SUN Dianzhu,DONG Xuezhu.Meshing analysis of real tooth surface[J].Chinese Journal of Mechanical Engineering,2000,36（8）：98-100.(in Chinese)

[13]苏智剑,吴序堂,毛世民,等.基于齿面参数化表示的准双曲面齿轮的设计 [J].西安交通大学学报,2005,39（1）:17-20.

SU Zhijian,WU Xutang,MAO Shimin,et al.Design of hypoid gear tooth surface represented by non-uniform rational B-spline polynomial[J].Journal of Xi'an Jiaotong University,2005,39（1）:17-20.(in Chinese)

[14]张军辉,方宗德,王成.基于NURBS的弧齿锥齿轮真实齿面的数字化仿真 [J].航空动力学报,2009,24（7）:1672-1676.

ZHANG Junhui,FANG Zongde,WANG Cheng.Digital simulation of spiral bevel gears'real tooth surfaces based on Non-Uniform Rational B-Spline[J].Journal of Aerospace Power,2009,24（7）:1672-1676.(in Chinese)

[15]刘光磊,沈允文,王三民.弧齿锥齿轮齿面网格加密的双三次样条法 [J].机械科学与技术,2000,19（增刊1）:128-129.

LIU Guanglei,SHEN Yunwen,WANG Sanmin.Double Third-power spline used to add more nodes to the surface mesh of a spiral bevel gear[J].Mechanical Science and Technology for Aerospace Engineering,2000,19（Suppl 1）:128-129.(in Chinese)

[16]刘光磊,沈允文,王三民.刚支时弧齿锥齿轮齿面啮合迹的确定[J].机械科学与技术,2001,20（3）:392-394.

LIU Guanglei,SHEN Yunwen,WANG Sanmin.Determination of contacting path of spiral bevel gears on rigid support[J].Mechanical Science and Technology for Aerospace Engineering 2001,20（3）:392-394.(in Chinese)

[17]刘光磊,王三民,孙智民,等.确定弧齿锥齿轮齿面啮合迹的改进算法[J].机械设计,2000（9）:13-15.

LIU Guanglei,WANG Sanming,SUN Zhimin,et al.An improved method for ascertaining the contacting path of spiral bevel gears[J].Journal of Machine Design,2000（9）:13-15.(in Chinese)

[18]朱心雄.自由曲线曲面造型技术 [M].北京:科学出版社,2001：138-169.

ZHU Xinxiong.Free curves and surfacesmodeling technology[M].Beijing:Science Press,2001：138-169.(in Chinese)