一类具有庇护所效应的阶段结构时滞Holling-III型捕食-食饵模型的稳定性和Hopf分支
2017-09-26张秋华
张秋华,周 恺
(池州学院 数学与计算机学院,安徽 池州 247000)
一类具有庇护所效应的阶段结构时滞Holling-III型捕食-食饵模型的稳定性和Hopf分支
张秋华,周 恺①
(池州学院 数学与计算机学院,安徽 池州 247000)
利用对平衡点处特征方程特征根的判断,给出一类具有庇护所效应的阶段结构时滞Holling-III型捕食-食饵模型局部稳定性的条件,并进一步给出模型在正平衡点处产生Hopf分支的条件.
捕食-食饵系统;阶段结构;时滞;局部稳定性;Hopf分支
0 引言
众所周知,捕食-食饵系统是种群动力学中的一类重要模型,已经被许多数学及生物学家广泛研究.在自然现象中,生物种群经常处于不同的阶段,如哺乳阶段、成熟阶段等;另一方面,在种群动力学中,时间滞后也是不容忽视的一个因素.结合上面两点,近年来,越来越多的学者开始关注更为实际的具有阶段结构的时滞捕食-食饵系统[1-3].
1946年,Crombic通过实验的方法较早地将庇护所效应引入了食饵-捕食者模型.所谓“庇护所效应”指的是,在一些捕食-食饵系统中,食饵种群总是会进入一些所谓的安全区域,即不会被捕食者捕食的区域,体现出的作用就是有助于保持食饵种群的数量规模,一定程度上保持了自然群落的生物多样性.文献[4]建立了具有庇护所效应的捕食-食饵模型,讨论了庇护所中食饵数量与现有食饵数量呈正比例的情形.文献[5-6]研究了具有庇护所效应的Lotka-Volterra捕食-食饵模型,得出了庇护所效应能够增加系统的稳定性的结论.特别地,文献[7]研究了食饵具有庇护所效应的阶段结构时滞Beddington-DeAngelis型捕食-食饵模型

的局部稳定性和Hopf分支问题.由于在脊椎动物的种群动力学研究中,通常采用Holling-III型功能性反应函数,本文将研究具有庇护所效应的阶段结构时滞Holling-III型捕食-食饵模型

的局部稳定性和Hopf分支问题,其中x1(t),x2(t)和y(t)分别表示未成熟食饵、成熟食饵和捕食者的种群密度,a是未成熟食饵的自然增长率,r1,r2和r分别代表三个种群的死亡率,b表示从未成熟种群向成熟种群过渡的转化率,α为成熟种群内部的竞争率,β(1-m)是捕食者的捕获率,d表示捕食者捕获到生长的转化率.假设系统(2)满足初始条件:

其中R3+={(x1,x2,y):x1≥0,x2≥0,y≥0}.
1 E0和E1的局部稳定性
在判断各平衡点的稳定性之前,我们先给出一些假设条件:


如果(H2)、(H3)成立,则系统(2)存在唯一的正平衡点其中


相应特征方程为

特征方程(3)在平衡点E0(0,0,0)处变成下面形式:

如果(H1)成立,则(4)式的所有根均具有负实部,从而平衡点E0是局部渐近稳定的;如果(H2)成立,则(4)式至少有一个正根,所以E0是不稳定的.

当(H2)成立时,方程的两个根均具有负实部.方程(5)的其余根由方程确定.记

如果(H2)、(H3)成立,容易验证:F(0)<0,且有F(λ)→+∞(λ→+∞),所以方程F(λ)=0至少有一个正实根.从而方程(5)至少有一个正实根,故E1不稳定.如果(H2)、(H4)成立,则F(0)>0,由文献[8]知,对于所有的τ≥0,边界平衡点E1是局部渐近稳定的.总结上面的讨论,有下面结论.
定理1对于方程(2),有如下结论:
(i)当(H1)成立时,方程(2)的零平衡点E0(0,0,0)是局部渐近稳定的,当(H2)成立时,E0是不稳定的;
(ii)当(H2)、(H4)成立时,方程(2)的边界平衡点是局部渐近稳定的,当(H2)、(H3)成立时,平衡点E1是不稳定的.
2 E*的局部稳定性和Hopf分支
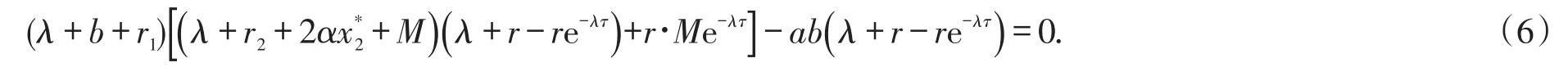
(6)式进一步可转化成

为了方便起见,将(7)式写成下面形式:

其中

2.1 τ=0时

由Routh-Hurwitz准则可知,当(P2+Q2)(P1+Q1)-(P0+Q0)>0时,正平衡点E*是局部渐近稳定的.
2.2 τ>0时
令λ=iω(ω>0)是方程(8)的根,则

将(9)的实部和虚部分离,得到

进一步,有
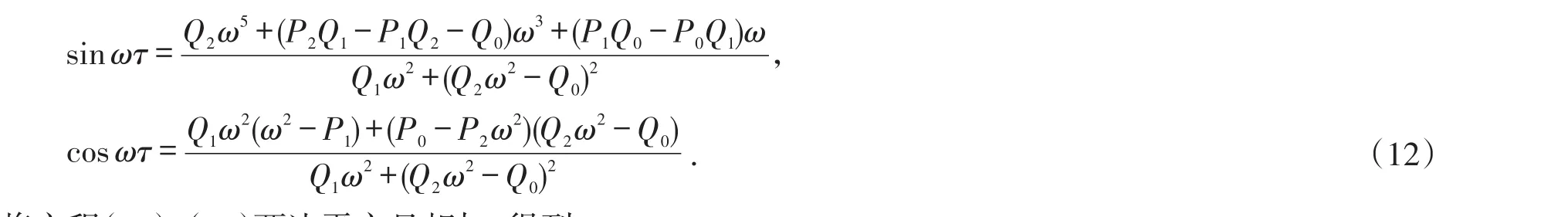
将方程(10)、(11)两边平方且相加,得到

其中

显然,当条件(H5)成立时,,则(13)式无正实根.因此,由文献[8]知,对所有的τ≥0,正平衡点E*是局部渐近稳定的.当(H6)成立时,有P0-Q0<0,则方程(13)存在唯一的正根ω0.由(12)式可知,

记
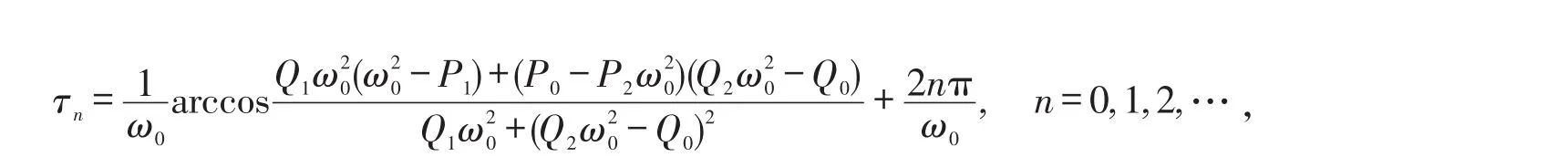
则±iω0是方程(8)在τ=τn时的一对纯虚根.因此,方程(8)除了在τ=τ0时有根±iω0外,在τ∈[0,τ0)时所有根均具有负实部.从而,当时,正平衡点E*在τ∈[0,τ0)时保持稳定.下面断言:
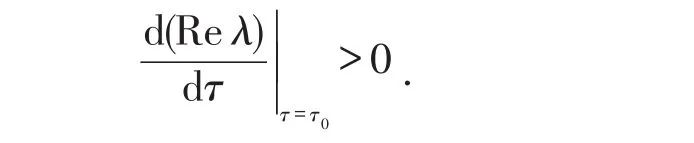
在方程(8)两边关于τ求导(注意到λ是τ的隐函数),得到

进一步可得,

从而,进一步计算可得,

由(10)和(11)式易知,

从而,

因此,横截条件成立,故在ω=ω0,τ=τ0时产生Hopf分支.综合上面的分析,得到下面定理:
定理2 对于方程(2),当(H3)、(H5)成立时,对于所有的τ≥0,方程(2)的正平衡点都是局部渐近稳定的;当(H3)、(H6)成立时,存在τ0>0,使得平衡点E*在τ∈[0,τ0)时是局部渐近稳定的,且当τ=τ0时,方程(2)在E*处产生Hopf分支.
[1]HU Haijun,HUANG Lihong.Stability and Hopf bifurcation in a delayed predator–prey system with stage structure for prey[J].Nonlinear Anal RWA,2010,11:2757-2769.
[2]WANG Wendi,CHEN Lansun.A predator-prey system with stage structure for predator[J].Comput Math Appl,1997,33:83-91.
[3]XU Rui,CHAPLAIN M A J,DAVIDSON F A.Global stability of a Lotka-Volterra type predator–prey model with stage structure and time delay[J].Appl Math Comput,2004,159:863-880.
[4]COLLINGS J B.Bifurcation and stability analysis of temperatures dependent mite predator-prey interaction model incorpo⁃rating a prey refuges[J].Bull Math Biol,1995,57(1):63-76.
[5]HAUSRATH A.Analysis of a model predator-prey system with refuges[J].Math Anal Appl,1994,181(2):531-545.
[6]HUANG Yunjin,CHEN Fengde,LI Zhong.Stability analysis of a prey-predator model with Holling type III response func⁃tion incorporating a prey refuges[J].Appl Math Comput,2006,182(1):672-683.
[7]WEI Fengying,FU Qiuyue.Hopf bifurcation and stability for predator-prey systems with Beddington-DeAngelis type func⁃tional response and stage structure for prey incorporating refuge[J].Appl Math Modelling,2016,40(1):126-134.
[8]KUANG Y.Delay differential equations with applications in population dynamics[M].New York:Academic Press,1993.
Stability and Hopf Bifurcation for a Delayed Predator-prey System with Holling-III Type Functional Response and Stage Structure for Prey Incorporating Refuge
ZHANG Qiuhua,ZHOU Kai
(School of Mathematics and Computer,Chizhou University,247000,Chizhou,Anhui,China)
By analyzing the character equations at different equlibria,we obtain the stability and Hopf bifurca⁃tion conditions for a delayed predator-prey system with Holling-III type functional response and stage struc⁃ture for prey incorporating refuge.
predator-prey system;stage structure;delay;local stability;Hopf bifurcation
O 175.1
A
2095-0691(2017)03-0001-05
2017-02-23
2014年安徽省高校优秀青年人才支持计划项目(皖教秘人[2014]181);安徽省教育厅高校自然科学研究项目(KJ2016A517);安徽省自然科学基金项目(1708085QA13)
张秋华(1981- ),男,安徽无为人,硕士,讲师,研究方向:随机微分方程.
