基于CEEMD和小波包阈值的组合降噪及泄流结构的模态识别方法

胡剑超， 练继建， 马 斌， 董霄峰

(天津大学 水利工程仿真与安全国家重点实验室，天津 300072)

基于CEEMD和小波包阈值的组合降噪及泄流结构的模态识别方法

胡剑超， 练继建， 马 斌， 董霄峰

(天津大学 水利工程仿真与安全国家重点实验室，天津 300072)

水流荷载激励下，泄流结构模态识别的实测振动信号常受噪声干扰。以往EEMD算法有添加白噪声造成非标准IMF导致的模态分裂问题及IMF有噪声残余不能完整重构信号的完备性问题。而完备总体经验模态分解(CEEMD)法，通过在信号分解的每一层面添加特定高斯白噪声，利用分解后第一阶分量加总平均得到唯一余量计算固有模态函数，克服了EEMD的缺点；同时提出CEEMD与小波包阈值结合的组合降噪方法，运用到向家坝水弹性模型实测振动信号降噪中，验证了该组合方法降噪的有效性；为了提高带噪振动响应模态识别的精度，基于数据相关技术，利用Markov参数构造相关矩阵R，用该相关矩阵重构Hankel矩阵后SVD分解得到系统最小实现，即数据相关特征系统实现法(ERA/DC)。将滤波降噪结合模态识别的整套方法，应用到锦屏一级拱坝的泄流实测振动响应中，得到了较好的应用效果。

泄流结构；滤波降噪；完备总体经验模态分解；小波包；模态识别；相关特征系统实现法

水工结构的模态参数识别是确认结构运行健康状态的重要技术手段。由于数据采集环境复杂以及大型泄流结构激励难等状况，必须消除或降低振动响应信号中的噪声影响并在未知输入激励条件下进行水工结构的模态识别。

李成业等[1-3]研究的EMD/EEMD(Empirical Mode Decomposition With Ensemble EMD)+小波的滤波降噪方法具有诸多优点：EEMD具有克服模态混叠、完全自适应及IMFs都是单分量函数的特点，能弥补小波在处理非平稳信号上的不足；同时小波变换具有多分辨率分析的优点，利用小波阈值函数滤波，克服了EMD/EEMD滤除噪声时，容易损失有用信号的缺点。

然而该组合方法仍有不足之处。EEMD通过原始信号中添加高斯白噪声改进EMD算法[4]。郑近德等[5]指出这种方法使得分解后的信号包含残余噪声；每步构造添加的白噪声不同造成IMF分解数量不同，使得总体平均后的IMF不符合标准定义产生模态分裂；EEMD不能完整的重构原始信号，不具完备性。基于多尺度分析的小波变换，通过尺度由大到小、时域-频域变换的过程，由粗到精的展现信号的特征。然而由文献[6]中小波算法可知，其只能对低频小波细节子空间进一步分解，而信号的高频部分则没有予以考虑。

由于方法自身的局限性，使得EEMD+小波阈值组合去噪方法在泄流结构振动响应分析中受到一定的限制。为了克服EEMD的缺点，Torres等[7]提出完备总体模态经验分解法(CEEMD)，而小波包变换[8](Wavelet Dacket Transform, WPT)既对信号低频尺度又对高频部分进行精细分解。本文提出的基于CEEMD和小波包阈值的组合滤波降噪方法，不仅继承了EEMD加小波方法的优点，还改进了该方法不足之处。文中通过向家坝水弹性模型实测振动信号降噪，证明改进组合降噪方法更加有效。

Lian等[9]运用特征系统实现法(Eigensystem Realization Algolithm, ERA)，根据水工结构工作状态下只受环境激励(如水流脉动荷载)的特点，仅用拱坝泄流响应成功进行了模态识别。ERA实质是利用脉冲或自由衰减响应数据，构造广义Hankel矩阵进行奇异值SVD分解，寻找系统的最小实现。Hankel矩阵的维数与模型阶次相关联，影响着系统矩阵A是否为系统最小实现，最终决定模态识别精度。若系统输入响应中混有噪声时，对Hankel矩阵影响较大[10]。Juang[11-12]用相关响应数据R代替脉冲响应数据，构造数据相关Hankel矩阵进行SVD分解，即数据相关特征系统实现法(ERA/DC)。本文结合泄流激励下水工结构振动特点，将ERA/DC引入泄流结构模态参数识别中。并将基于组合降噪的ERA/DC应用于锦屏一级拱坝实测振动响应分析中，得到了精确的识别结果。

1 完备总体模态经验分解法CEEMD

以EEMD为基础，CEEMD算法原理如下：

步骤1：x[n]为离散数n的原始信号；定义算子Ej(·)表示信号EMD分解后第j阶IMF；wi[n](i=1,…,I)是单位方差零均值高斯白噪声；εk系数是各阶段信噪比；

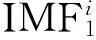
(1)

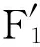
步骤4：对于一阶余量r1[n]中添加白噪声信号，构造信号r1[n]+ε1E1(wi[n])并进行EMD分解，加总平均后得到第二阶固有模态函数分量：

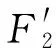
(2)

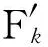
步骤6：对k阶余量rk[n]中添加白噪声信号，有构造信号rk[n]+εkEk(wi[n])，进行EMD分解，得到第k+1个固有模态函数分量：

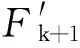
(3)

步骤7：回到步骤(5)，计算下一个k。算法构造循环取第一阶IMFs分量加总平均，避免了EEMD同时分解的IMFs数量不同造成的模态分裂问题；

步骤8：重复步骤5～步骤7，直到余量不能再分解为止，最终得到：

(4)

式中：R是最终余量；K是固有模态分量总数。目标信号x[n]可以表示为

(5)

式(5)为原始信号x[n]得到精确重构，即该方法是具有完备性的分解方法。

下面结合一简单算例验证CEEMD方法的优越性。设采样频率为200 Hz、采样时间5 s的原始信号x，混入白噪声k后得到含噪信号z，表达式如下：

z=x+k=3sin(πt)+5sin(2πt)+4.5sin(8πt)+5randn(1,1 000)

信号x，z如图1，染噪信号z分别用EMD、EEMD、CEEMD方法滤波降噪(EEMD与CEEMD添加相同标准差与数量的白噪声，一般取0.01倍～0.5倍原信号标准差，添加次数100～300次)，滤波后与x对比，如图2所示。

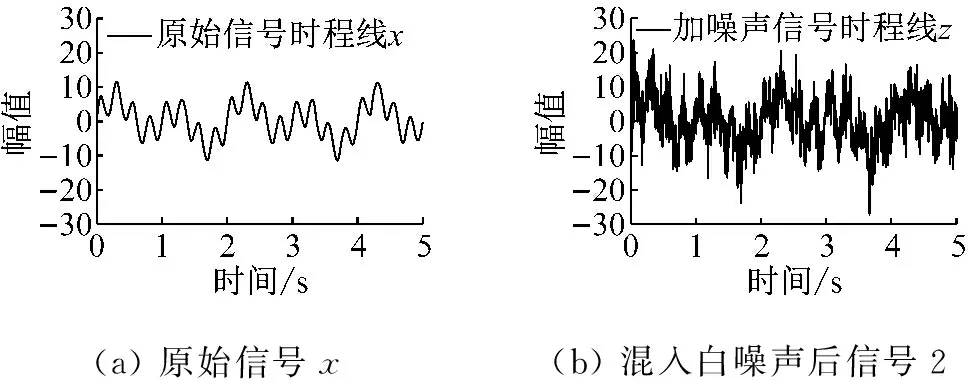
(a)原始信号x(b)混入白噪声后信号2

图1 原始信号x与混入白噪声后信号z

Fig.1 Original signalxand signalzmixed white noise

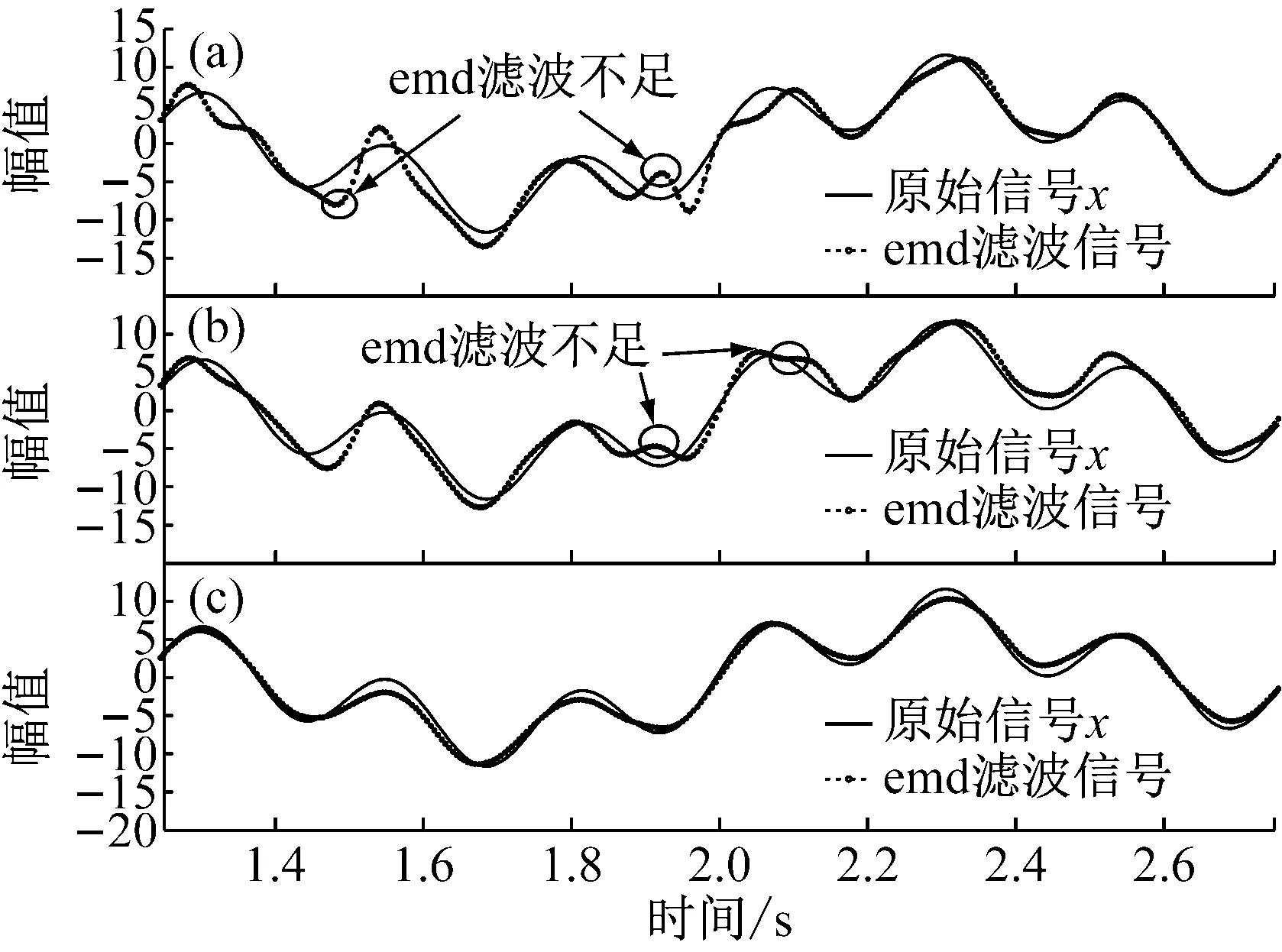
图2 三种方法滤波降噪信号图(局部)

从图2(a)、图2(b)可知，EMD或EEMD 方法滤波降噪都有不足之处，而图(c)中CEEMD滤波降噪的重构信号与原信号x波形最为接近。CEEMD方法改进了EEMD不足之处，得到了显著优于EMD以及EEMD的滤波结果。

2 小波包(WPT)阈值滤波方法

小波包变换阈值滤波效果主要受阈值的影响。阈值函数可分为硬阈值函数和软阈值函数。软阈值降噪可实现最优估计，保证降噪后的重构信号与原信号有同样的平滑，且不会产生附加震荡，其表达式为

(6)

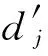
3 CEEMD与WPT阈值的组合滤波方法

坝体振动主要受表中孔水流脉动荷载激发，该脉动荷载是具有一定频带宽度的平稳随机过程，表现为有色白噪声谱的性质。坝体动力响应通常是低频或平稳的振动信号，而环境噪声常为非平稳的高频信号。

CEEMD将实测振动响应信号的不同频率模量由高到低自适应清晰分离，分离出的带有噪声污染的信号固有模态分量，可利用小波包阈值的滤波方法有效去除噪声。该方法适用于水工结构的振动信号滤波降噪处理，有利于下一步水工结构模态精确识别。

基于CEEMD和WPT的组合滤波降噪方法步骤如下：

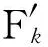
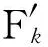
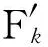
下面结合向家坝消力池内导墙水弹性模型验证文中组合滤波方法的有效性，如图3所示。

图3 向家坝水弹模型隔振系统与右消力池内导墙模型

Fig.3 Vibration isolation system of Xiang JiaBa hydroelastic model and Guide wall hydroelastic model in the right stilling basin

为了研究向家坝水电站泄洪诱发场地振动规律，天津大学水利工程系建造了1∶80比尺的向家坝水弹性模型。为了减小外界振源对坝体振动信号的干扰，采取在水弹模型混凝土基础四周设置隔振沟、模型上下游连接段由止水橡胶软连接等隔振措施，见图3。试验证明，该减振隔振系统有效减小了隔振沟外振动源的干扰[13]。

向家坝采用消力池消能，见图3，右消力池内设置一导墙水弹模型。导墙长宽高为99 cm×4 cm×38 cm。材料模拟碾压混凝土，弹模为105 MPa，泊松比0.167。布设4个动位移测点。选择测点4在上游水位370 m、表孔开度6 m工况实测导墙动位移响应数据进行分析，采样频率200 Hz，取10 s数据分析。

图4 实测导墙振动信号与添加噪声后振动信号

由于设置减振隔振系统，该动位移实测响应数据x(n)的“毛刺”很少，信号较为光滑，可认为其基本不含噪声信号，如图4(a)。在实测信号x(n)中加入白噪声k，受噪声污染信号z=x(n)+k(SNR=3.39 dB)，如图4(b)所示，针对染噪信号z，分别用CEEMD、小波包(WPT)阈值、EEMD+小波、CEEMD+WPT四种方法进行滤波降噪。

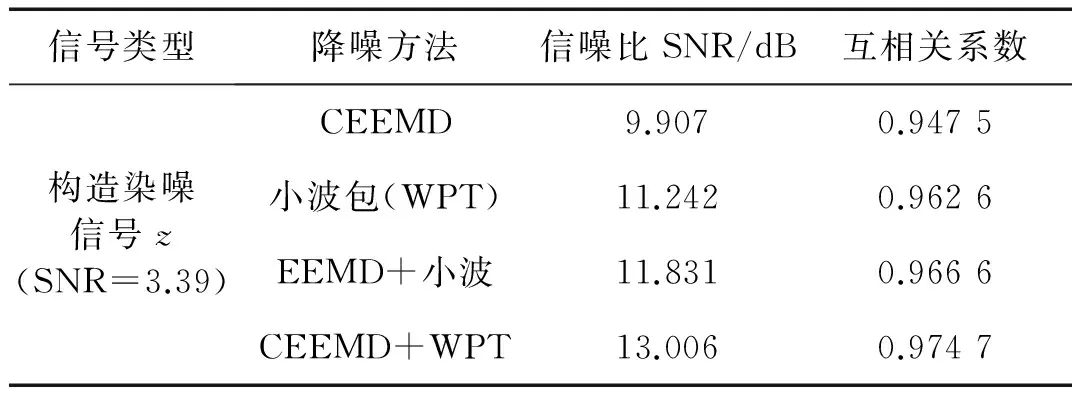
图5为各方法滤波重构波形与原信号x对比，表1为信噪比SNR、滤波信号与原始信号x互相关系数。

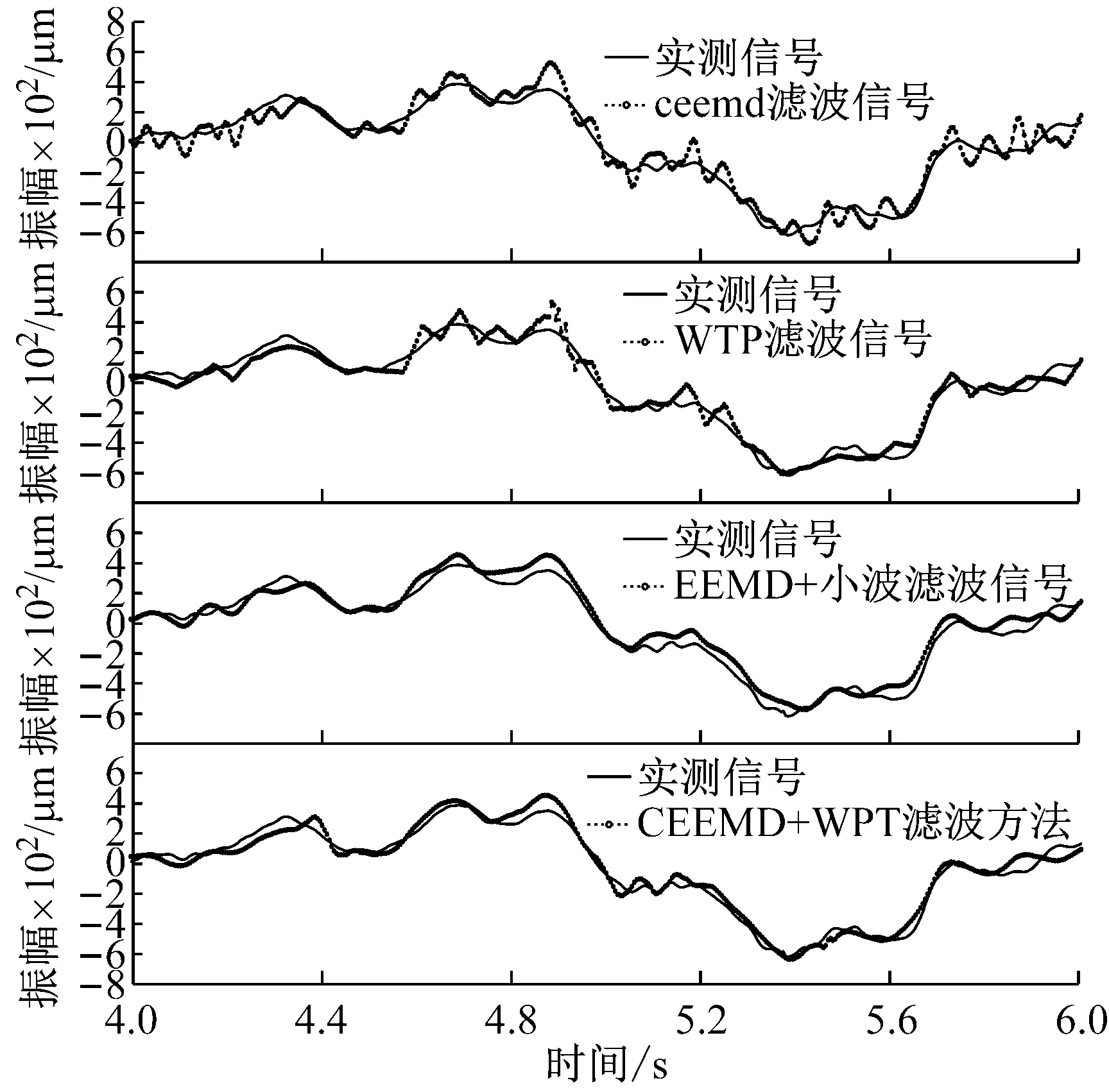
图5 四种方法滤波降噪对比图(局部)

信号类型降噪方法信噪比SNR/dB互相关系数构造染噪信号z(SNR=3.39)CEEMD9.9070.9475小波包(WPT)11.2420.9626EEMD+小波11.8310.9666CEEMD+WPT13.0060.9747

由四种方法滤波降噪后的振动信号与原始信号x(n)对比图5看出：CEEMD分解加带通滤波的做法，得到的SNR较低，重构信号仍有较多毛刺，说明加入的噪声有残留且部分有用信号也被一并去除；小波包阈值滤波的信噪比大于CEEMD，但重构波形仍存在毛刺；EEMD+小波的滤波方法，SNR较高，信号波形重构较好、毛刺基本消除，说明噪声基本被滤除，原始信号保留较好；而CEEMD+WPT的组合滤波降噪振动信号，白噪声“毛刺”不仅被很好的滤除干净，从信噪比SNR=13.006 dB、相关系数=0.974 7来看，原始振动信号x(n)保留最好、降噪效果最佳。

4 基于ERA/DC的泄流结构模态参数识别方法

4.1数据相关特征系统实现法(ERA/DC)算法原理

根据振动理论，线性系统的脉冲响应函数矩阵，即马可夫参数(Markov)为

Y0=D,Y1=CB,Y2=CAB,…,

Y(k)=CAk-1B

(7)

式中：Y(k)为l×m阶矩阵，又是脉冲响应函数矩阵。A为系统矩阵、B为输入矩阵、C为输出矩阵。由有限维线性时不变系统状态方程知，系统模态识别问题即为系统的最小实现问题，即求得矩阵A，B，C并使其阶次最小。由Markov参数Y(k)，构造分块Hankel矩阵：

(8)

式中：H(k-1)为lξ×mη阶矩阵，ξ和η为任意整数。当令k取1时，有Hankel矩阵H(0)。在ERA方法中，会针对H(0)进行SVD分解。而在ERA/DC方法中，则构建γ=lξ维方阵R(q)：

R(q)=H(q)HT(0)

(9)

式中：数据相关矩阵R(q)为lξ×lξ维，Hankel矩阵H(0)、H(q)为lξ×mη阶矩阵。当Hankel矩阵的列数很大时，R(q)的维数将≪H(q)。若当q=0时，有：

R(0)=H(0)HT(0)=

(10)

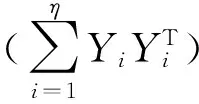
构建(α+1)×(β+1)阶块相关矩阵U(q)：

U(q)=

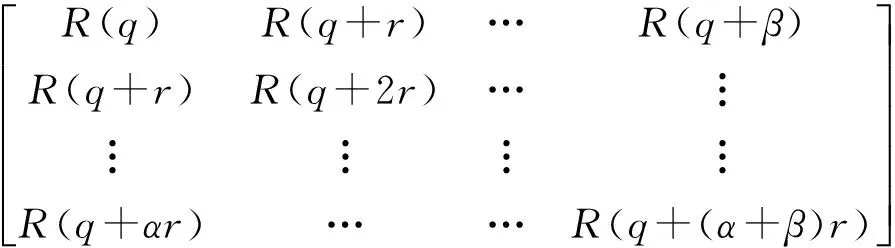
(11)

式中：q为避免有噪声存在时相关矩阵产生偏移的整数；r为防止相邻R块产生重叠的整数；α和β为分析中包含多少相关延迟。针对U(0)矩阵SVD分解：

U(0)=PDQT

(12)

式中：左奇异矩阵P和右奇异矩阵Q的维数为(α+1)γ×n和(β+1)γ×n，奇异值对角矩阵D为n×n阶方阵。构造U(0)伪逆矩阵U†，代入式(16)～式(18)推得：

A=D-1/2PTU(1)QD1/2

B=[EγTPD1/2]†H(0)EmC=EpTPD1/2

(13)

式中：EγT=[Iγ0γ]，EmT=[Im0m]，EpT=[Ip0p]，Iγ表示γ阶单位矩阵，0γ表示γ阶零矩阵。

针对系统矩阵A进行奇异值分解，求得特征值矩阵Z=diag(Z1,Z2,…,Zn)，系统特征值与矩阵A特征值有关系：λi=ln(Zi)/T，T为采样间隔。求得模态参数为

有阻尼频率：ωdi=imag(λi)

阻尼比：ξi=-Re(λi)/|λi|

(14)

式中：Re(·)为取实部，imag(·)为取虚部，|·|表示取模。ERA/DC与ERA算法的主要区别在于首先进行数据相关运算后重构Hankel矩阵U(0)，这样可压缩矩阵规模，减少奇异值分解的计算时间，并减少噪声影响。相较于ERA，ERA/DC具有更好的识别精度。

4.2基于组合降噪的ERA/DC模态识别方法

ERA/DC通过Markov参数(即为脉冲响应函数)进行模态参数识别。水工结构在泄流激励下振动时，可假定为线性时不变系统，利用自然激励技术(NExT)将参考点和响应点数据变换为测点间的互相关函数，得到结构的脉冲响应函数。

在未知输入激励下，结构的振动模态阶次通常是未知的。原始信号由延时嵌陷技术重构的吸引子轨道矩阵D，与ERA方法中Hankel矩阵H(0)的构造形式一致，基于奇异熵定阶技术，H(0)的定阶(即系统的定阶)可根据奇异熵增量的变化进行。观察式11可知，ERA/DC用相关R矩阵构造的Hankel矩阵，当q=0时，U(0)的矩阵形式与H(0)相同，因此由ERA/DC进行结构模态识别，同样可根据奇异熵增量谱确定系统阶次。

为了进一步减少实测信号中噪声影响，模态识别之前须对响应数据运用CEEMD+WPT的组合滤波方法进行降噪，这就是基于组合降噪方法的ERA/DC泄流结构模态识别方法，其流程如图6所示。

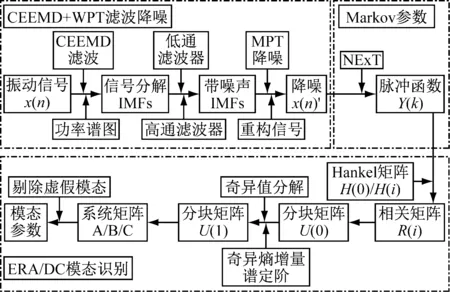
图6 CEEMD加小波包组合滤波后的信号

为了说明ERA/DC方法针对带噪信号识别的优越性，建立混凝土悬臂梁有限元模型验证。梁长20.0 m、截面尺寸1.4 m×0.6 m、动弹模30 GPa。梁的一端全约束固定，如图7。为了充分激发梁的各阶模态，沿梁轴线选择六个点P1～P6施加负Y向的典型水流脉动荷载，荷载频率100 Hz，时长30 s，如图8所示。

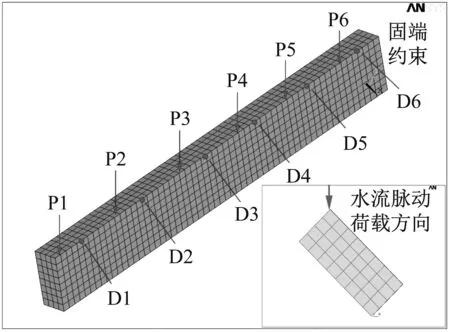
图7 悬臂梁有限元模型与荷载施加方向图

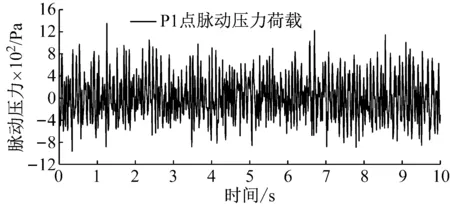
图8 典型水流脉动荷载时程线图(局部)

计算悬臂梁动力响应，提取悬臂梁D1～D6测点振动信号。以靠近悬臂梁固端的D6为参考点，其与梁中间D4测点的时程线如图9，用NExT法计算D4-D6的脉冲响应函数如图10(a)所示。

得到脉冲响应函数后计算奇异熵增量随阶次的变化如上图10(b)所示，奇异熵阶次为9阶时，熵增量开始缓慢增长并趋于平稳，说明信号的有效特征信息量已经趋于饱和，特征信息已经基本完整。剔除特征值中的非模态项(非共轭根)和共轭项(重复项)后，利用模态置信因子MAC准则判别虚假模态[14]。得出结构的前3阶振动阶次进行对比，如表2所示。

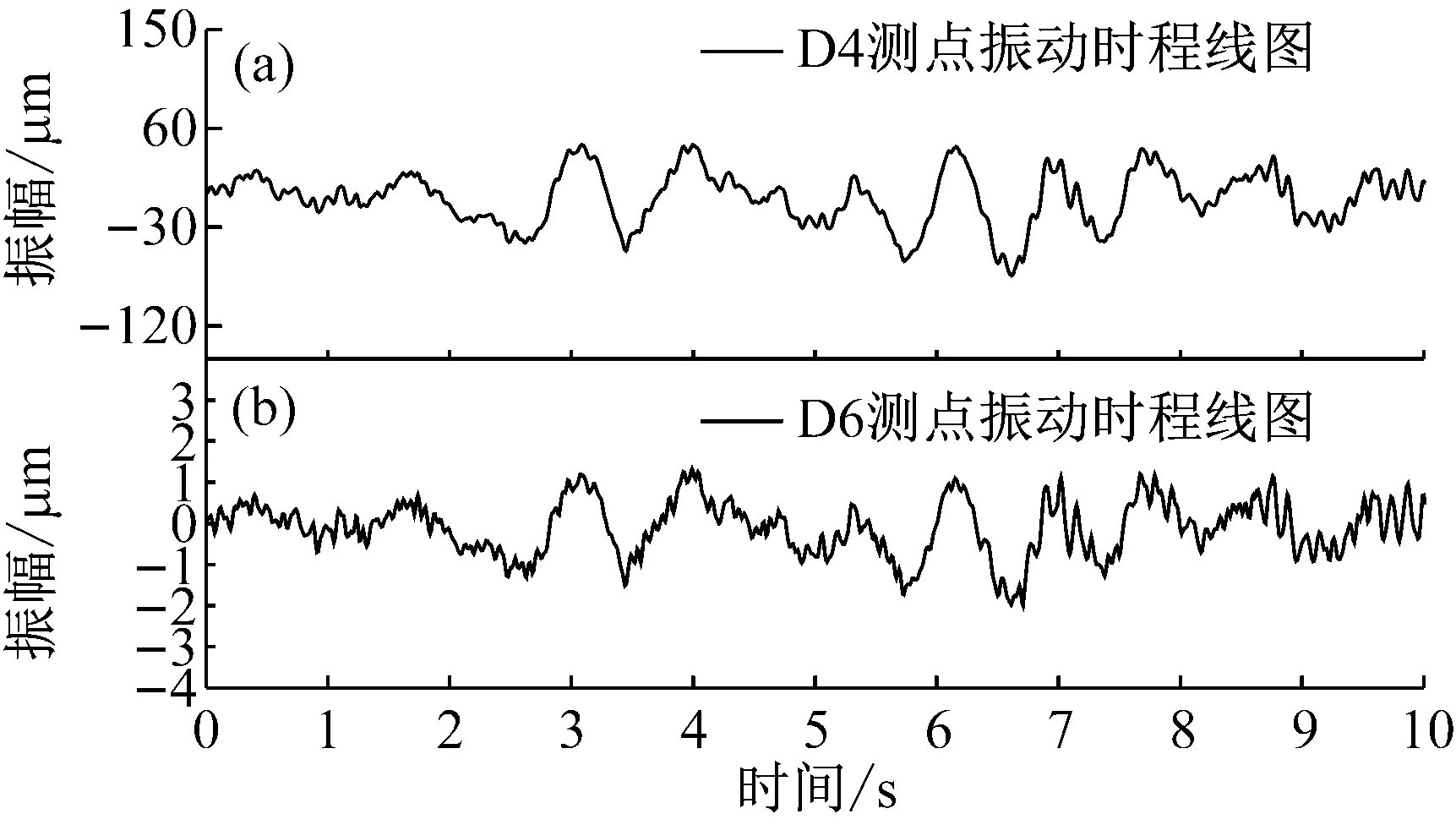
图9 测点D4与D6振动时程线图(局部)

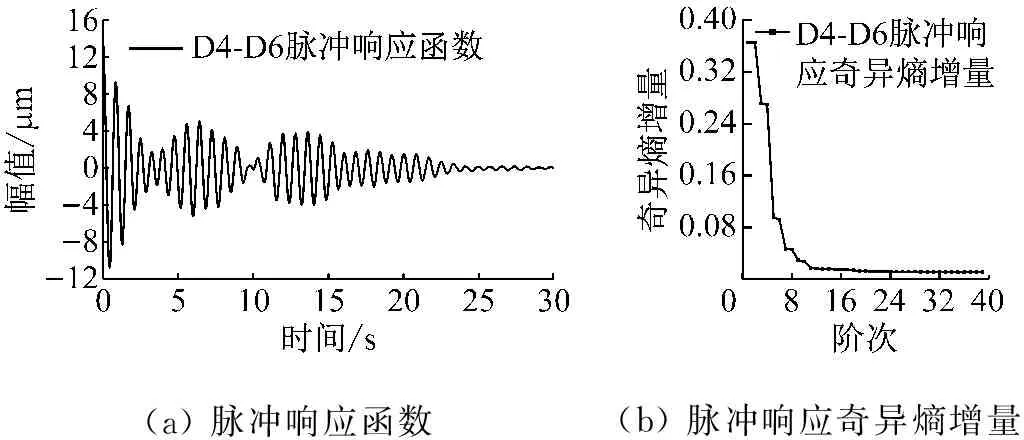
(a)脉冲响应函数(b)脉冲响应奇异熵增量

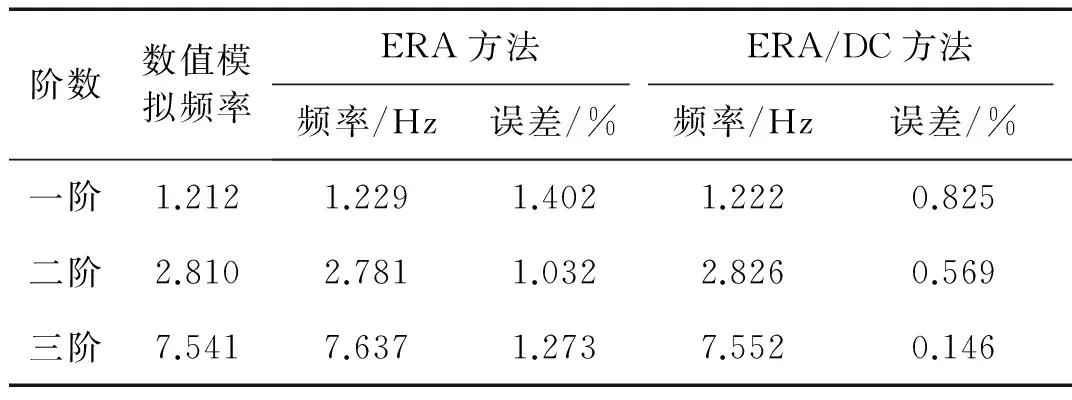
图10 D4-D6点的脉冲响应函数与奇异熵增量谱图

由表2可知，ERA法识别频率误差<2%，而 ERA/DC方法频率识别误差<1%，都准确识别出了悬臂梁前三阶模态。

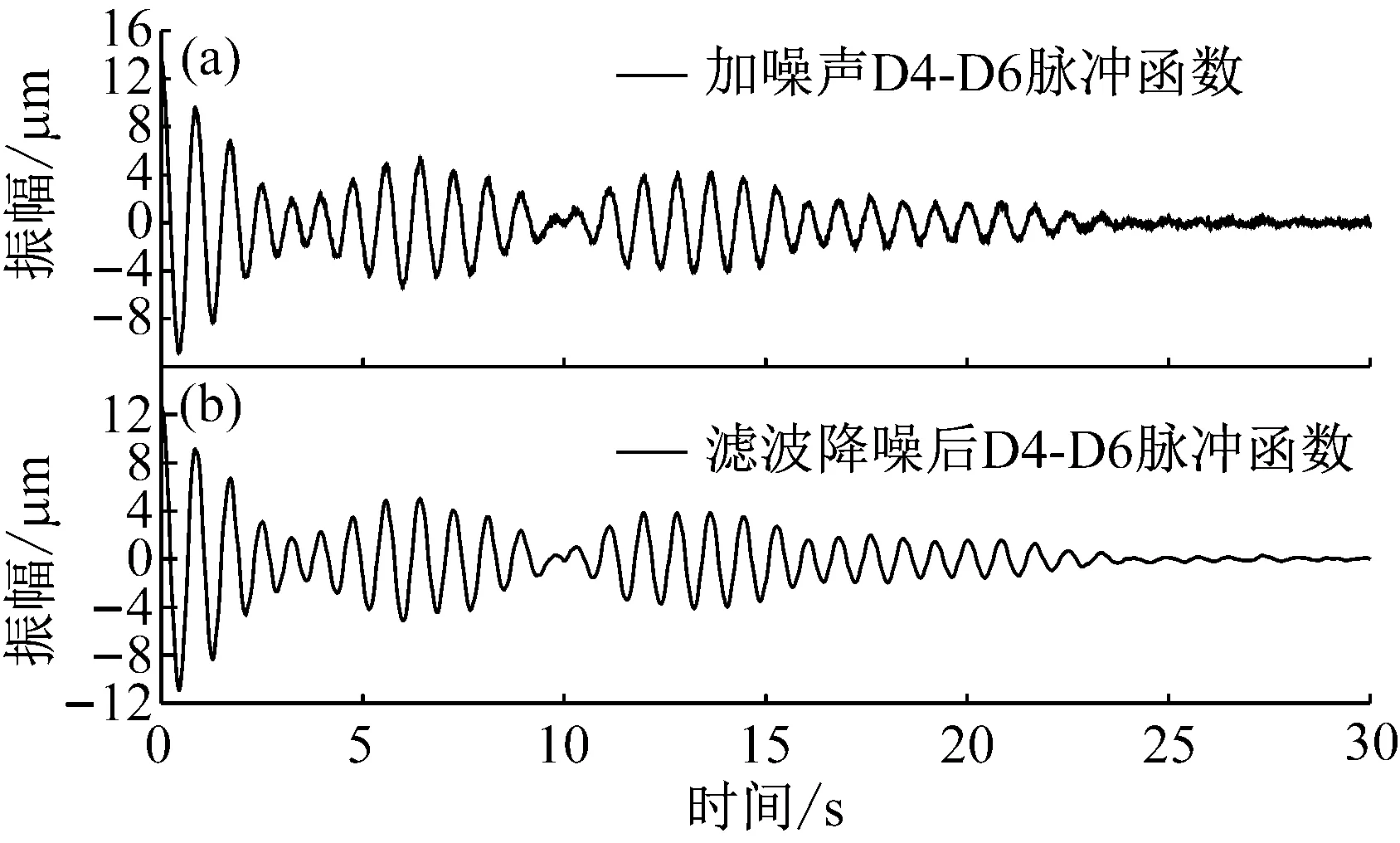
图11 添加噪声脉冲函数信号与滤波降噪信号

为了对比振动信号受到噪声污染情况下，ERA与ERA/DC方法的识别精度，将D4-D6脉冲响应函数添加白噪声(信噪比SNR=20 dB)，信号如图11(a)所示。运用两种方法模态识别，结果如表3所示。

表3带噪脉冲响应信号的模态频率识别对比(SNR=20)

Tab.3Modalfrequencyidentificationofpulse-responsesignalmixednoise(SNR=20dB)

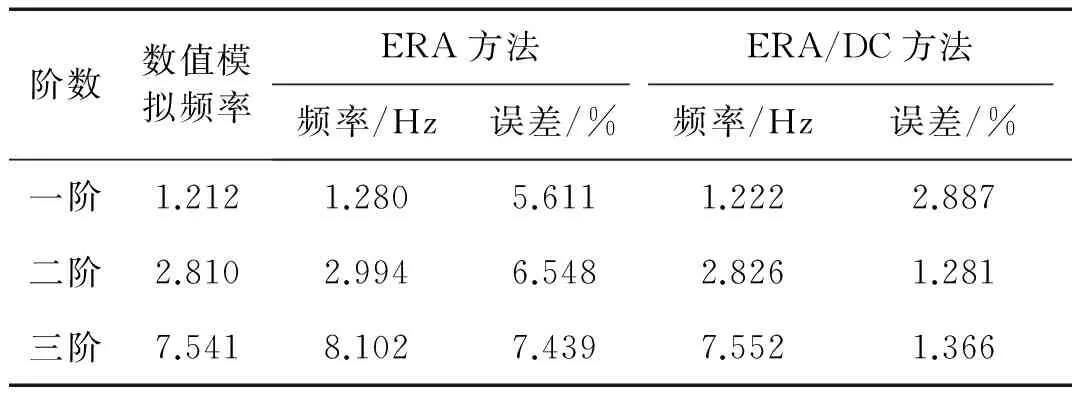
阶数数值模拟频率ERA方法ERA/DC方法频率/Hz误差/%频率/Hz误差/%一阶1.2121.2805.6111.2222.887二阶2.8102.9946.5482.8261.281三阶7.5418.1027.4397.5521.366

由表3看出，信号受噪声污染后，ERA识别悬臂梁三阶模态频率，相较于无干扰情况误差显著增大。其一阶、三阶误差都>5%，第三阶误差>7%。ERA/DC识别中，三阶误差都<3%，表明其模态识别抗噪声干扰能力强于ERA方法。

将该染噪脉冲函数信号(D4点)用CEEMD+小波包组合降噪，结果如图11(b)所示。滤波后信号信噪比SNR=25.538、相关系数0.998 6。模态识别结果，如表4所示。

表4滤波脉冲函数响应信号模态频率识别对比

Tab.4Frequencyidentificationoffilteringpulse-responsesignal

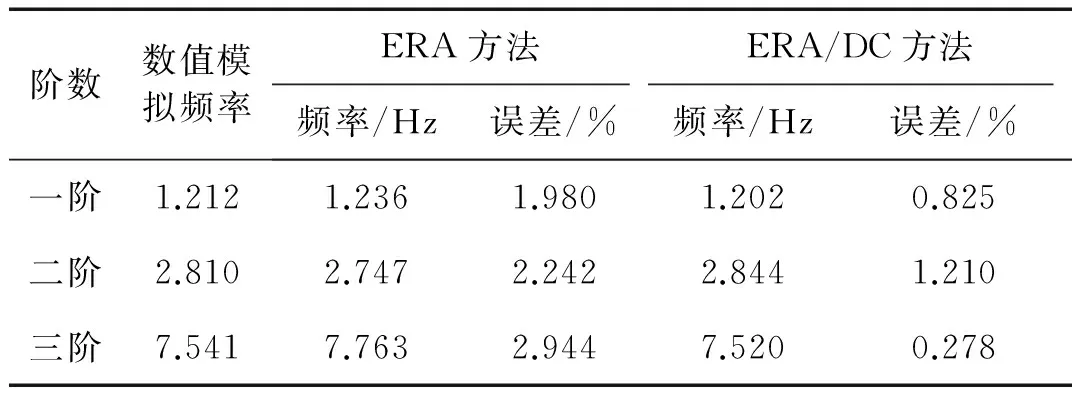
阶数数值模拟频率ERA方法ERA/DC方法频率/Hz误差/%频率/Hz误差/%一阶1.2121.2361.9801.2020.825二阶2.8102.7472.2422.8441.210三阶7.5417.7632.9447.5200.278

染噪信号滤波后识别结果由表4可知：ERA方法识别中，频率误差降至<3%，ERA/DC频率识别误差降至<1.5%，证明该组合降噪方法与ERA/DC方法结合的有效性与必要性。

5 锦屏一级拱坝实测振动信号应用分析

锦屏一级水电站是雅砻江干流下游河段的控制性梯级电站。其最大坝高305 m，是目前世界最高的混凝土双曲拱坝。2014年天津大学水利工程系针对锦屏一级枢纽工程进行了水力学原型观测。沿坝顶1#～24#坝段，水平向顺水流布设H1～H7共7个坝顶动位移传感器。水库汛期泄洪期间，实测了不同泄流工况下，泄流激励下坝体振动响应。传感器测点布置图及锦屏一级拱坝有限元模型，如图12所示。

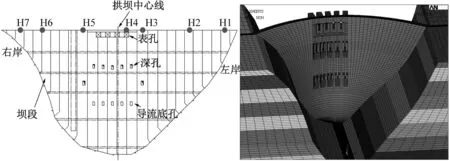
图12 传感器测点布置及锦屏一级拱坝有限元模型图

5.1滤波降噪

流激振动造成的拱坝动位移均方根通常为几十个微米。由于振动量级较小，混入的干扰信号和背景噪声容易淹没有用信号。分析各工况坝体振动规律：拱冠梁处振动最大但远离干扰源，坝肩振动量小且易受噪声干扰。因此选取工况7(3#表孔25%开度、泄流量329 m3/s、上游水位1 879.2 m、下游1 645.6 m)时，拱冠梁附近参考测点H3及右坝肩附近测点H6，采样频率200 Hz，时长40 s，其时程线及归一化功率谱，如图13所示。

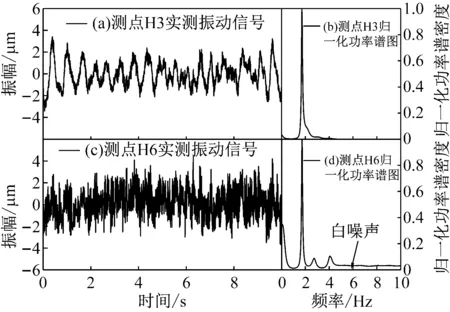
图13 H3、H6测点振动信号(局部)及归一化功率谱图

由锦屏有限元模态计算得拱坝前六阶模态频率，频率范围在1.0～3.5 Hz之间。测点H3位于拱冠梁附近，受到噪声干扰小，由其功率谱图13(b)可知其振动能量集中在1.0～3.0 Hz频带部分，与有限元计算相符。

在现场泄流观测期间，发现右坝肩附近存在少量施工作业。坝肩测点H6振动信号“毛刺”较多，并出现漂移现象，运用最小二乘拟合法消除趋势项后如图13(c)。功率谱如图13(d)，<0.5 Hz的低频部分有能量集中，且>4.5 Hz处有宽频白噪声存在，直接应用H6实测振动数据进行模态识别会产生很大误差。

为了得到拱坝真实振动信号，运用文中提出的组合滤波降噪方法滤除原始信号中的噪声。将H6测点信号CEEMD分解，添加白噪声标准差1.494 μm，添加数300次，最大迭代数5 000次。分解得IMF1～IMF13分量，IMFs分量从高频到低频依次排列如上图14。

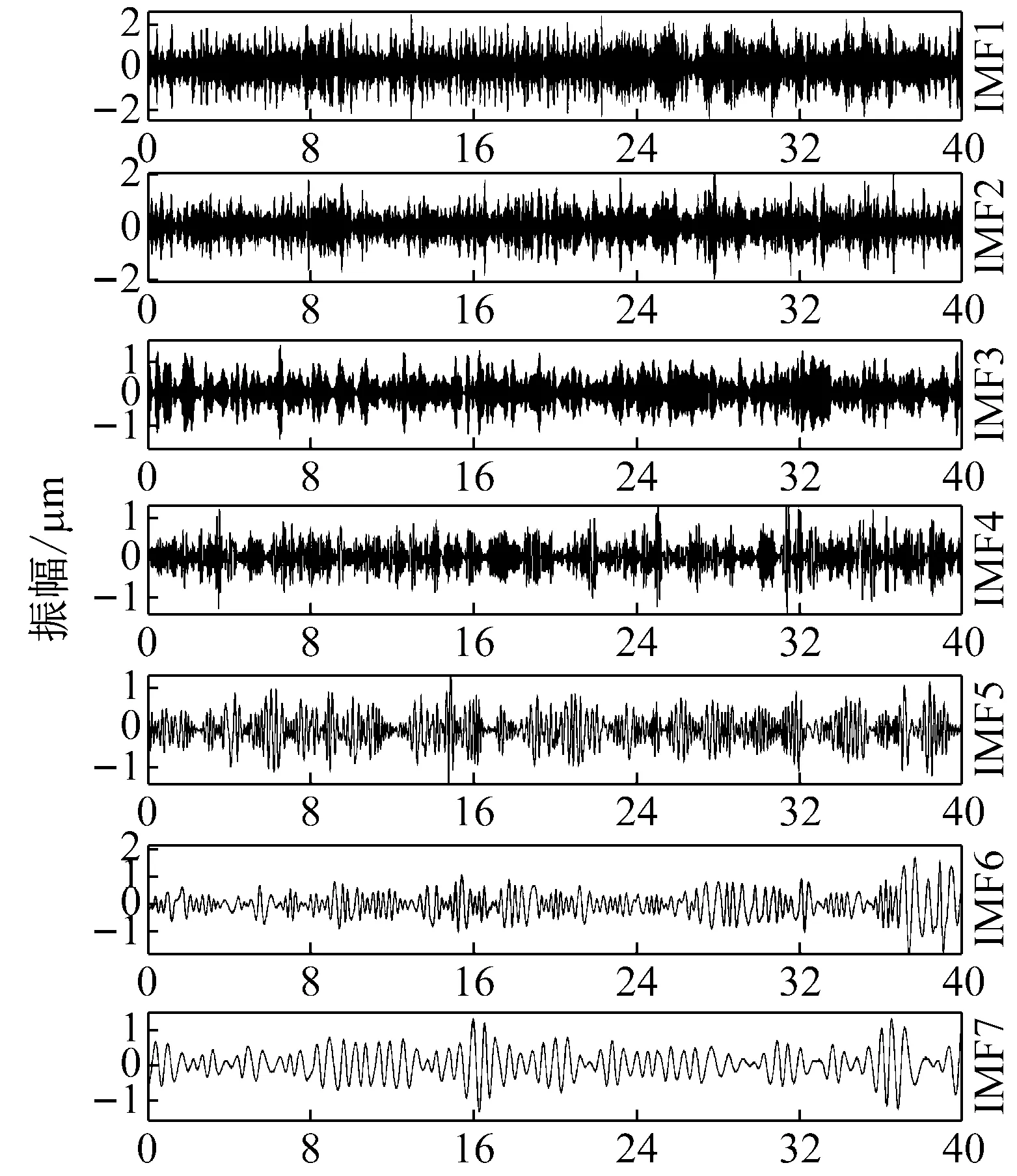
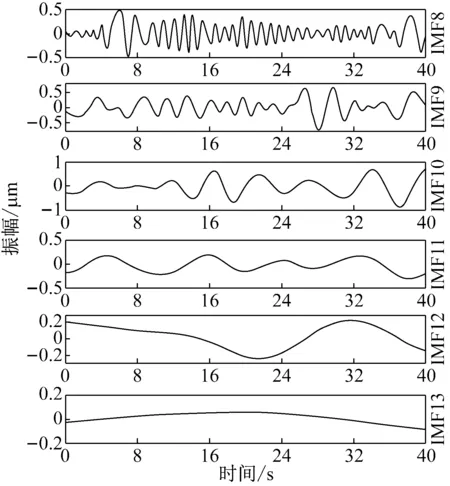
图14 H6测点实测信号CEEMD分解图

做出IMF1～IMF12分量归一化功率谱图如下图15所示。前两阶IMF能量集中在高频且频带很宽，为宽频白噪声分量，运用低通滤波进行滤除。IMF3～IMF6是振动信号分量，但其中混入了大量噪声信号，需要运用WPT方法进一步滤除噪声。IMF7～IMF9分量振动能量集中在1.0～3.0 Hz附近，判断其属于结构真实振动信号。而IMF10～13为低频趋势项干扰，予以高通滤除。

IMF3～IMF6混有白噪声，运用小波包阈值方法进一步降噪。小波包分解采用dbN小波基，共N层分解，不同IMF分量采用不同的N值。采用软阈值方法，默认全局阈值。滤波后，由IMF3～IMF9重构信号如图16所示。

从图16可知，原始信号毛刺被去除。从功率谱曲线可知，低频干扰噪声和高频白噪声被有效消除了，响应中反映结构模态信息的共振分量所占的比重大大增强。

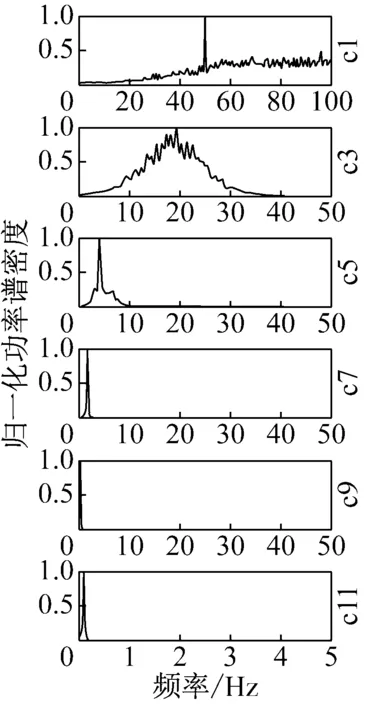
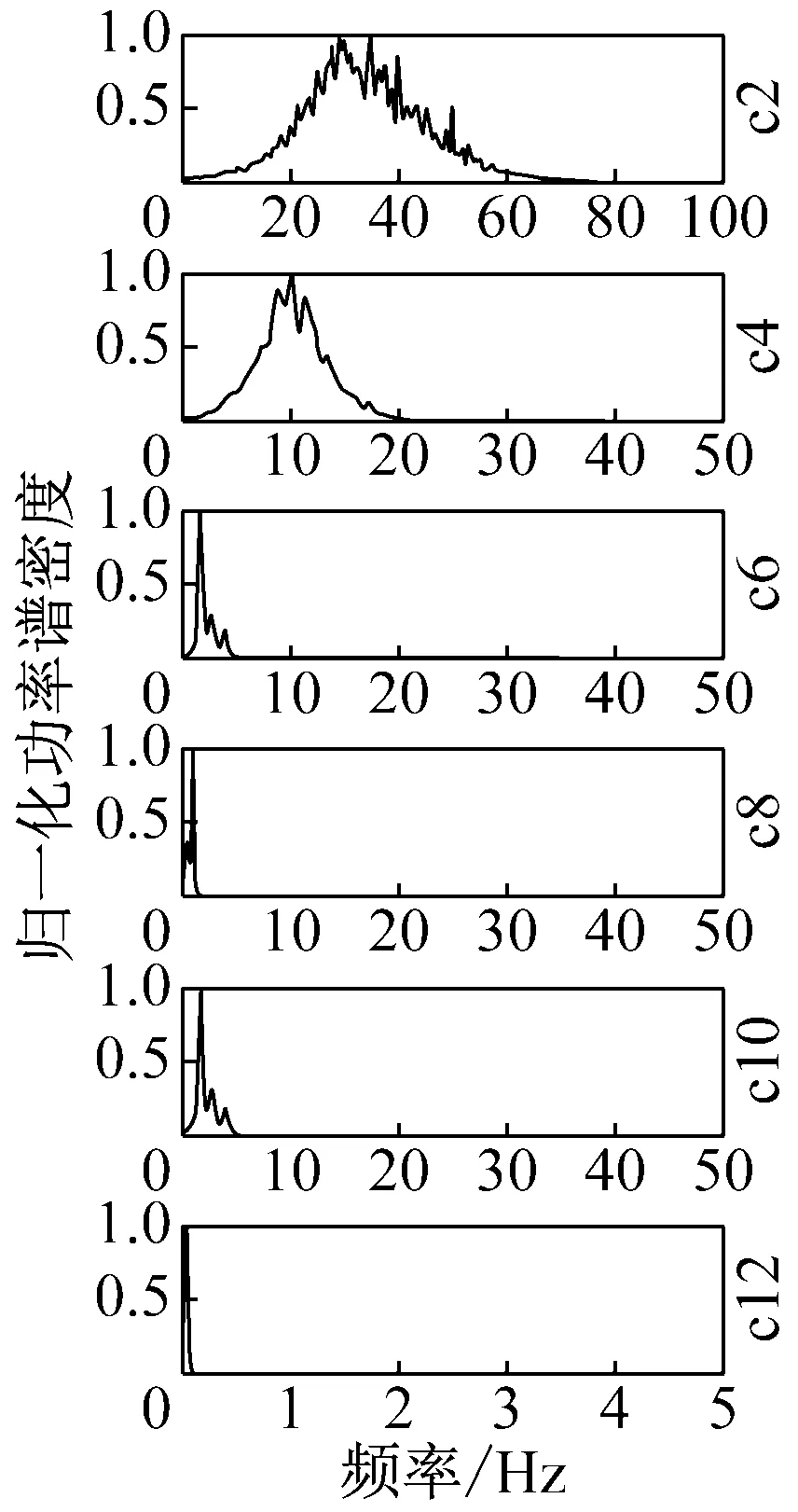
图15 H6信号IMF分量归一化功率谱图

图16 H6组合滤波降噪振动信号(局部)及功率谱图

5.2模态识别

由图17可知，H6测点实测振动响应滤除噪声信号后，以拱冠梁附近的测点H3为参照点，运用NExT方法计算H3与H6测点脉冲响应函数；由H6-H3脉冲响应函数，首先构造4 000×4 000阶Hankel矩阵H(0)以及2 000×2 000阶Hankel矩阵U(0)，计算奇异熵增量随阶次变化。确定奇异熵阶次为11阶，采用文中ERA/DC方法进行识别。剔除非模态项和共轭项后用MAC准则判别虚假模态，得到结构前6阶振动阶次，识别结果列于表5。表5还列出了拱坝有限元模态计算结果，并将该振动信号同时运用ITD、STD、Prony(复指数法)、ARMA(时序分析法)、SSI(随机子空间法)与ERA(特征系统实现法)进行模态识别，识别结果一同列于表5中。

图17 H3-H6测点脉冲响应函数与奇异熵增量谱

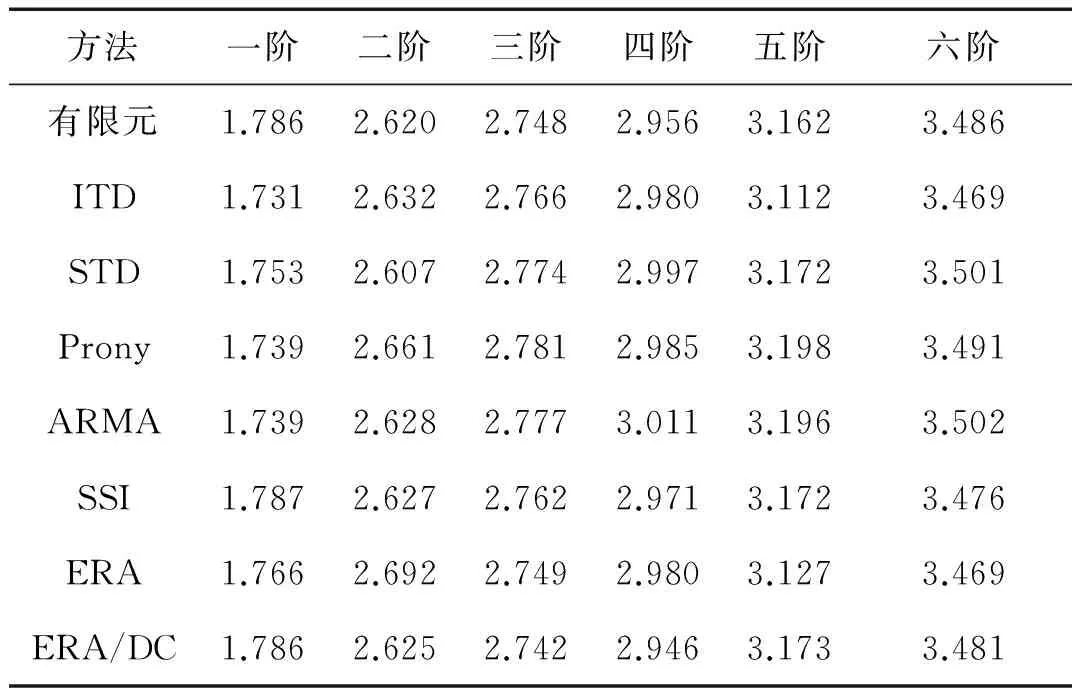
表5 锦屏一级拱坝模态频率识别对比

拱坝是一种典型的密频结构，综合各方法的模态识别的结果，可得到锦屏一级拱坝的前六阶工作频率。可以看出，ERA/DC方法对于低频、密频具有较强的识别能力。

将各方法识别结果进行对比，发现识别结果都较为接近，都能识别出拱坝前六阶频率。而文中所提方法与拱坝有限元计算结果同样相吻合。文中方法的计算结果不仅能够满足工程分析的需要，且具有相对更好的计算精度。

6 结 论

本文针对泄流结构振动响应信号，提出一种组合滤波降噪结合模态识别的整套方法，应用到实际泄流结构的状态参数识别中，得到以下结论：

(1) CEEMD解决了EEMD算法导致的模态分裂及完备性问题，小波包能获得丰富的时频局部化信息，更适合突变信号、非平稳信号的分析与滤波。向家坝水弹性模型实测振动信号降噪说明，CEEMD+小波包阈值的组合降噪方法较EEMD+小波方法具有更好的滤波降噪效果。

(2) 基于数据相关技术的ERA/DC方法克服了泄流结构输入激励条件难获得的问题，利用悬臂梁振动模型进行验证，表明其对含噪信号具有比ERA更好的模态识别精度，同时说明了其与组合降噪方法结合的必要性。

(3) 将CEEMD+小波包阈值组合降噪方法结合ERA/DC模态识别方法，应用到锦屏一级拱坝泄流实测振动响应信号中，得到了很好的实际应用效果。

[1] 李成业，练继建，刘昉，等. EMD与小波阈值联合滤波方法的改进及其在泄流结构振动分析中的应用[J]. 振动与冲击，2013，32(9)：63-70.

LI Chengye, LIAN Jijian, LIU Fang, et al. An improved filtering method based on EMD and wavelet-threshold and its application in vibration analysis for a flood discharge structure[J]. Journal of vibration and shock, 2013, 32(9): 63-70.

[2] ZHANG Yan, LIAN Jijian, LIU Fang. An improved filtering method based on EEMD and wavelet-threshold for modal parameter identification of hydraulic structure[J]. Mechanical Systems and Signal Processing, 2016, 68: 316-329.

[3] 邵忍平，曹精明，李永龙. 基于EMD小波阈值去噪和时频分析的齿轮故障模式识别与诊断[J]. 振动与冲击，2012，31(8)：96-101.

SHAO Renping, CAO Jingming, LI Yonglong. Gear fault pattern identification and diagnosis using time-frequency analysis and wavelet threshold de-noising based on EMD[J]. Journal of vibration and shock, 2012, 31(8): 96-101.

[4] WU Z H, HUANG N E. Ensemble empirical mode decomposition: A noise assisted data analysis method[J]. Advances in Adaptive Data Analysis, 2009, 1(1): 1-41.

[5] 郑近德，程军圣，杨宇. 改进的EEMD算法及其应用研究[J]. 振动与冲击，2013，32(21)：21-26.

ZHENG Jinde, CHENG Junsheng, YANG Yu. Modified EEMD algorithm and its applications[J]. Journal of Vibration and Shock, 2013, 32(21): 21-26.

[6] OUADFEUL S A, ALIOUANE L. Random seismic noise attenuation data using the discrete and continuous wavelet transforms[J]. Arabian Journal of Geosciences, 2014, 7(7): 2531-2537.

[7] TORRES M E, COLOMINAS M A, SCHLOTTHAUER G, et al.A complete ensemble mode decomposition with adaptive noise[C] // IEEE International Conference on Acoustics. Speech and signal Processing(ICASSP). USA, NJ: IEEE. 2011. 4144-4147.

[8] HEMMATI F, ORFALI W, GADALA M S. Roller bearing acoustic signature extraction by wavelet packet transform, applications in fault detection and size estimation[J]. Applied Acoustics, 2016, 104(1): 101-118.

[9] LIAN J J,LI H K,ZHANG J W. ERA modal identification method for hydraulic structures based on order determination and noise reduction of singular entropy[J]. Science in China series E-Technological Sciences, 2009, 52(2): 400-412.

[10] 李蕾红，陆秋海，任革学.特征系统实现法的识别特性研究及算法的推广[J]. 工程力学，2002，19(1)：109-115.

LI Leihong, LU Qiuhai, REN Gexue. A study of eigensystem realization algorithm and its generalization[J]. Engineering Mechanics, 2002, 19(1): 109-115.

[11] JUANG J N, COOPER J E, WRIGHT J R. An eigensystem realization algorithm using data correlation (ERA/DC) for modal parameter identification[J]. Control Theory and Advanced Technology, 1988, 4(1): 5-14.

[12] CHIANG D Y, LIN C S. Identification of modal parameters from ambient vibration data using eigensystem realization algorithm with correlation technique[J]. Journal of Mechanical Science and Technology, 2010, 24(12): 2377-2382.

[13] 李淑君，练继建，欧阳秋平. 高坝泄流诱发坝区及场地振动的振源分析研究[J]. 水利水电技术，2014，45(9)：47-51.

LI Shujun, LIAN Jijian, OUYANG Qiupin. Study on source of dam discharge-induced vibration in dam region and site[J]. Water Resources and Hydropower Engineering, 2014, 45(9): 47-51.

[14] 董霄峰，练继建，杨敏，等. 海上风机结构工作模态识别的组合降噪方法[J]. 天津大学学报(自然科学与工程技术版)，2015，48(3)：203-208.

DONG Xiaofeng, LIAN Jijian, YANG Min, et al. A compound de-noising method for operational modal identification of offshore wind turbine structure[J]. Journal of Tianjin University(Science and Technology),2015,48(3):203-208.

Ade-noisingandmodalidentificationcombinedmethodbasedonCEEMDandwaveletpacketthresholdforflooddischargestructures

HU Jianchao， LIAN Jijian， MA Bin， DONG Xiaofeng

(State Key Laboratory of Hydraulic Engineering Simulation and Safety, Tianjin University, Tianjin, 300072 China)

Vibration signals measured for modal identification of a flood discharge structure under water load excitation are often interfered by noise. The EEMD algorithm has problems of modes splitting caused by nonstandard IMFs produced due to adding white noise and IMFs with residual noise not being able to completely reconstruct original signals. Here, the complete ensemble empirical mode decomposition (CEEMD) was proposed. Using it, the drawbacks of EEMD were overcome through adding a specific white noise to each stage of signal decomposition and using the unique residual obtained by adding the average to the first order component gained after decomposition to calculate IMFs. Furthermore, a de-noising method with CEEMD and the wavelet packet threshold combined was proposed to be applied in de-noising vibration signals measured from Xiangjia dam’s hydro-elastic model, the effectiveness of this method was verified. In order to improve the precision of modal identification with the noised vibration responses, based on the data correlation technology, Markov parameters were used to construct a correlation matrix R. The R matrix was employed to reconstruct a Hankel matrix. After its SVD, the minimum system realization was obtained. This algorithm was called the eigen-system realization algorithm with data correlation (ERA/DC). Finally, the proposed de-noising and modal identification combined method was applied in the measured vibration responses of Jinping arch dam to get a better application effect.

flood discharge structure; noise reduction; CEEMD; wavelet packet; modal identification; ERA/DC

国家重点基础研究发展计划(973计划)子课题“极端条件下高碾压混凝土坝动力响应机制”(2013CB035905-1)

2016-06-06 修改稿收到日期：2016-08-08

胡剑超 男，硕士生，1990年生

练继建 男，教授，博士生导师，1965年生

TV65

： A

10.13465/j.cnki.jvs.2017.17.001