具有褶皱薄弱段的正弦波纹梁吸能性能研究

周华志， 王志瑾， 韩 微， 江彬彬

(南京航空航天大学 飞行器先进设计技术国防重点学科实验室，南京 210016)

具有褶皱薄弱段的正弦波纹梁吸能性能研究

周华志， 王志瑾， 韩 微， 江彬彬

(南京航空航天大学 飞行器先进设计技术国防重点学科实验室，南京 210016)

薄弱环节的设置对波纹梁吸能性能的影响很大，好的薄弱环节可以降低波纹梁的冲击过载，从而降低结构传递给乘员的过载，并使波纹梁产生稳定的渐进压溃，以吸收更多的能量。提出了褶皱薄弱环节的概念，并对带有褶皱薄弱环节的波纹梁吸能性能进行了研究。对具有弧形薄弱段的波纹梁进行了有限元仿真，验证了仿真分析方法的正确性。在此基础上，建立了带有褶皱薄弱段的正弦波纹梁的有限元模型，对波纹梁几何参数对其吸能性能、坠毁冲击时的最大加速度的影响进行了研究。研究发现：褶皱薄弱环节能够有效降低波纹梁的最大冲击载荷，且对波纹梁吸能性能的影响不大。以上研究结果对波纹梁在吸能结构中的应用具有一定的指导意义。

波纹梁；抗坠撞；能量吸收；薄弱环节；几何参数

提高直升机的抗坠毁能力，是现代直升机，特别是武装直升机生存能力设计的主要要求之一。直升机抗坠毁设计过程中，机身设计非常关键。而机身设计中，机身下腹部所处的位置决定了它在坠撞时最有可能(不考虑起落架)先接触到地面，因而其吸能能力的设计就成为了机身结构适坠性设计的重中之重。

机身下腹部结构吸能主要是通过结构的大塑性变形和破碎来完成的。为了尽可能地减轻重量，直升机必须使用能量吸收率高的材料。在国内外学者的努力下，波纹梁结构[1-2]、薄壁管结构[3-5]、新型编织复合材料多胞结构(TCCSs)[6]、厚蜂窝和T型组合件[7]等具有高吸能性能的结构被开发出来，并在抗坠毁缓冲吸能结构中获得了广泛的应用。其中波纹梁结构因其优异的吸能性能和简单的制作工艺受到了尤为广泛的关注。

波纹梁结构最早是由荷兰的国家航空实验室(NLR)成功地在NH-90直升机的地板下结构中用作缓冲吸能元件。印春伟等[8]发现，复合材料的应用对波纹梁吸能能力的提升很明显；若在结构中引入薄弱环节，可使结构的破坏模式稳定可控。Zhou等[9]对石墨/环氧复材正弦波纹梁的冲击坠毁性能进行了试验和仿真研究。Gary等[10]给出了计算正弦波纹梁吸能性能的函数表达式。刘豫等[11]编制FORTRAN软件二次开发程序，对大尺寸复合材料RTM波纹梁进行了优化设计。孟祥吉等[12]基于MSC.Dytran开发了有限元程序，用于波纹梁的轴向冲击仿真，仿真结果与试验结果吻合得较好。冯振宇等[13]对四种不同的波纹梁的吸能性能进行了比较，发现正弦波纹梁的峰值载荷最低，吸能性能最好。卢致龙等[14-15]建立了含有复合材料本构关系的波纹梁有限元模型，采用Hashin准则判断材料的损伤，计算结果与试验结果吻合得较好。郑建强等[16]将波纹梁应用于民机机身耐撞性设计中，将波纹梁作为机腹隔框下端和蒙皮之间的吸能构件，客舱地板过载峰值相对较低, 有效缩短了最高过载脉宽。

王鑫伟等[17-20]对正弦波纹梁做了很多研究工作。他们运用MSC.Dytran有限元软件，用理想弹塑性材料来模拟复合材料的破坏过程和吸能能力，对长单波纹梁、短单波纹梁和三波纹梁的吸能能力进行了数值模拟。模拟结果和试验结果比较接近。在此基础上，他们对薄弱环节对波纹梁吸能能力的影响进行了研究，并提出了一种参数等效的方法用来模拟波纹梁盒段的耐撞性。

从以上的研究可见，波纹梁的薄弱环节对其吸能性能的影响很大，薄弱环节是波纹梁结构发生稳定的渐进压溃破坏，吸收大量能量的关键。本文提出了一种新的波纹梁薄弱环节，即褶皱薄弱环节。并采用有限元分析方法，对具有褶皱薄弱环节的正弦波纹梁的性能进行了研究；对各参数对其吸能能力的影响进行了分析和讨论。本文的研究对提高波纹梁吸能性能、降低抗坠毁结构的峰值过载具有一定的指导意义。

1 带褶皱薄弱环节的波纹梁结构

本文的研究对象为带有褶皱薄弱环节的正弦波纹梁，如图1所示。梁两端接近根部处加入了褶皱薄弱环节。图中：S为薄弱环节与梁端的距离；A为锯齿形线的长度；2λ为锯齿形线的顶角；D为波纹梁总长；H为波纹梁高度；R为波纹梁圆弧的半径，n为波纹数。

褶皱段作为薄弱环节的原理如下：在波纹梁承受轴向载荷F时，在褶皱段传力路径转折，会产生FAcos(λ)的弯矩。为平衡该弯矩，在波纹梁每半个波纹周期中，一半会产生正的附加应力，另一半会产生负的附加应力，由附加应力组成的弯矩来平衡褶皱段传力路径转折产生的弯矩。在此情况下，波纹梁在褶皱薄弱环节两端的轴向应力可如下表示：

(1)

式中:t为波纹梁的材料厚度；σax为由轴力F产生的应力；σex为附加应力，其大小与FAcos(λ)成正比，与波纹梁半波长L/2成反比；σ为总应力。

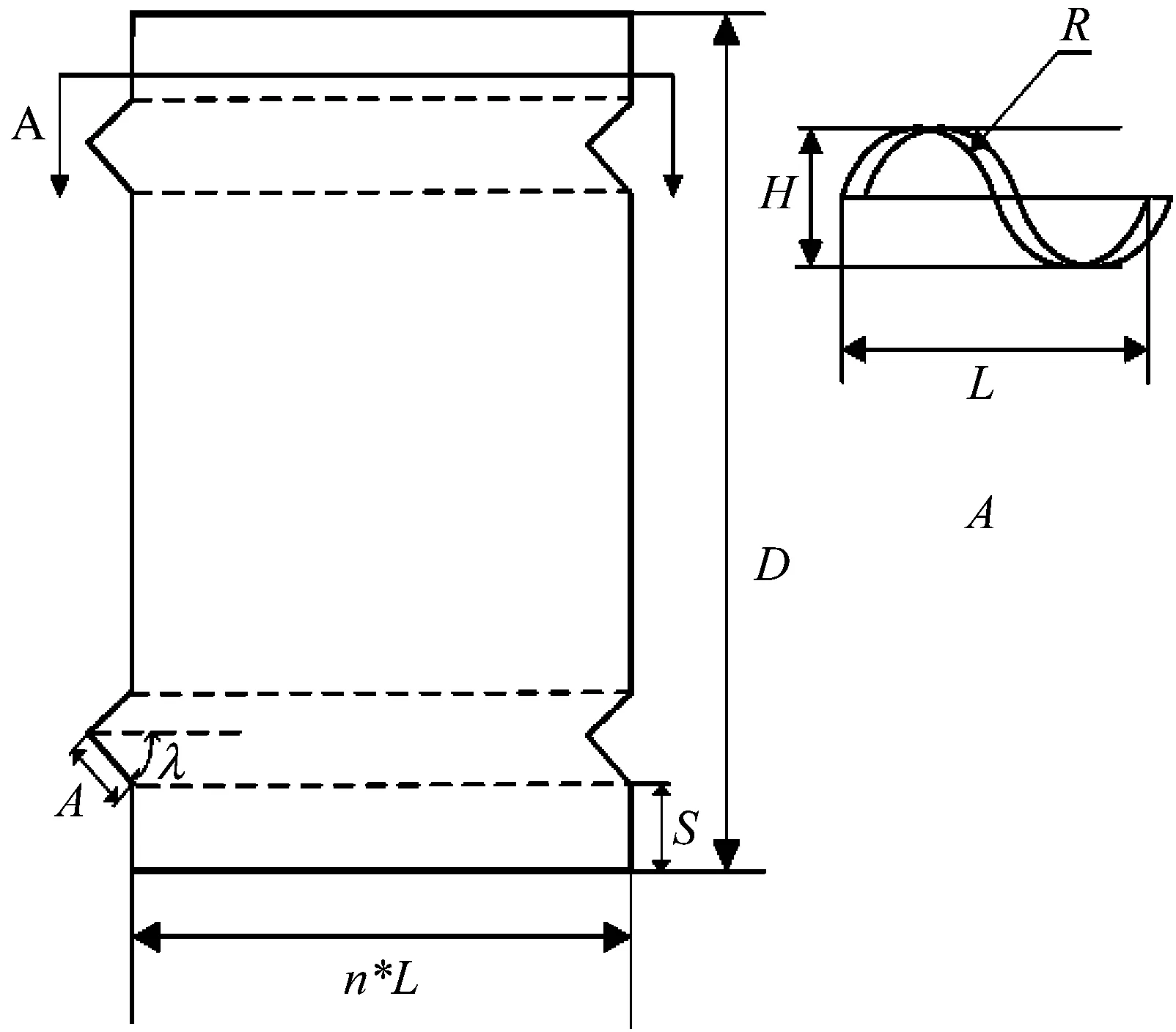
图1 正弦波纹梁几何参数

随着F的增大，总应力也会增大。当总应力达到材料的屈服应力时，由于附加应力的存在，载荷F会小于没有褶皱薄弱环节的情况，故褶皱段的轴向承载能力弱于波纹梁的剩余部分，可以作为薄弱环节使用。

当Acos(λ)较大时，附加应力也较大，其值可能会接近甚至超过σax。也就是说，通过调节A和λ，可以很方便的对薄弱环节的强度进行调节，实现波纹梁的稳定渐进破坏。

2 波纹梁有限元建模

2.1有限元建模

本文采用Python语言结合ABAQUS有限元分析软件进行有限元的参数化建模。模型中L=120 mm，D=160 mm。网格尺寸为2 mm。网格的类型选为四边形减缩积分壳单元S4R。

波纹梁沿轴向加载，在波纹梁加载方向两端各加一个刚性面板，以代表波纹梁的上下缘条及与其相连的其它结构，分析过程中不考虑这些结构的吸能性能，故将其简化为刚性面板。此外，下面板还起到刚性地面的作用。两面板与芯材之间通过接触约束连接，法向接触算法采用罚函数法，不允许面板和波纹梁接触后分离，切向摩擦因数取为无穷大，以模拟真实结构中波纹梁和缘条的共固化连接。在腹板和缘条之间传递沿轴向的压力的前提下，这样的简化是合理的。而在回弹开始后，腹板的变形、载荷等都相对较小，吸能过程已经结束，回弹开始后的过程相对而言并不重要。计算中涉及到芯材的大变形阶段，因此定义了芯材的自接触。

边界条件为下面板固支，上面板和波纹梁以6.5 m/s的初速度向下运动，以模拟面板与芯材接触并压缩芯材的过程。上面板上设置集中质量，质量的大小按照每米波纹梁397.6 kg计算。该质量是按照某型直升机地板下梁结构尺寸及载荷计算出来的。最终的有限元模型如图2所示。

图2 带褶皱薄弱环节的波纹梁有限元模型

2.2材料性能

波纹梁所用材料为碳纤维-环氧树脂复合材料。为简化模型，在文献[18]中复合材料被等效为弹塑性材料，取复材沿轴向的压缩模量(44.5 GPa)和强度(360 MPa)作为理想弹塑性材料的力学性能参数，取复材的密度(1 450 kg/m3)作为理想弹塑性材料的密度。本文采用同样的处理方式。材料厚度为1.6 mm。

在ABAQUS中，分别使用Elastic模块及Plastic模块定义材料的弹塑性行为，将材料定义为理想弹塑性材料。

2.3仿真结果

为了验证模型的正确性，取文献[18]中的带有圆弧薄弱环节的短波纹梁模型参数建立有限元模型，将仿真得到的上面板速度-时间曲线、波纹梁能量-时间曲线和文献[18]中的数据进行了比较。具体见图3～图4所示。为说明下缘条和地面用一个刚性面板模拟的影响，将下缘条和地面分别建模(模型中共三个面板)和合并建模(模型中共两个面板)计算得到的上面板加速度-时间曲线如图5所示。从图5中可以看出，边界条件的变化对回弹之前的加速度曲线的影响不大。

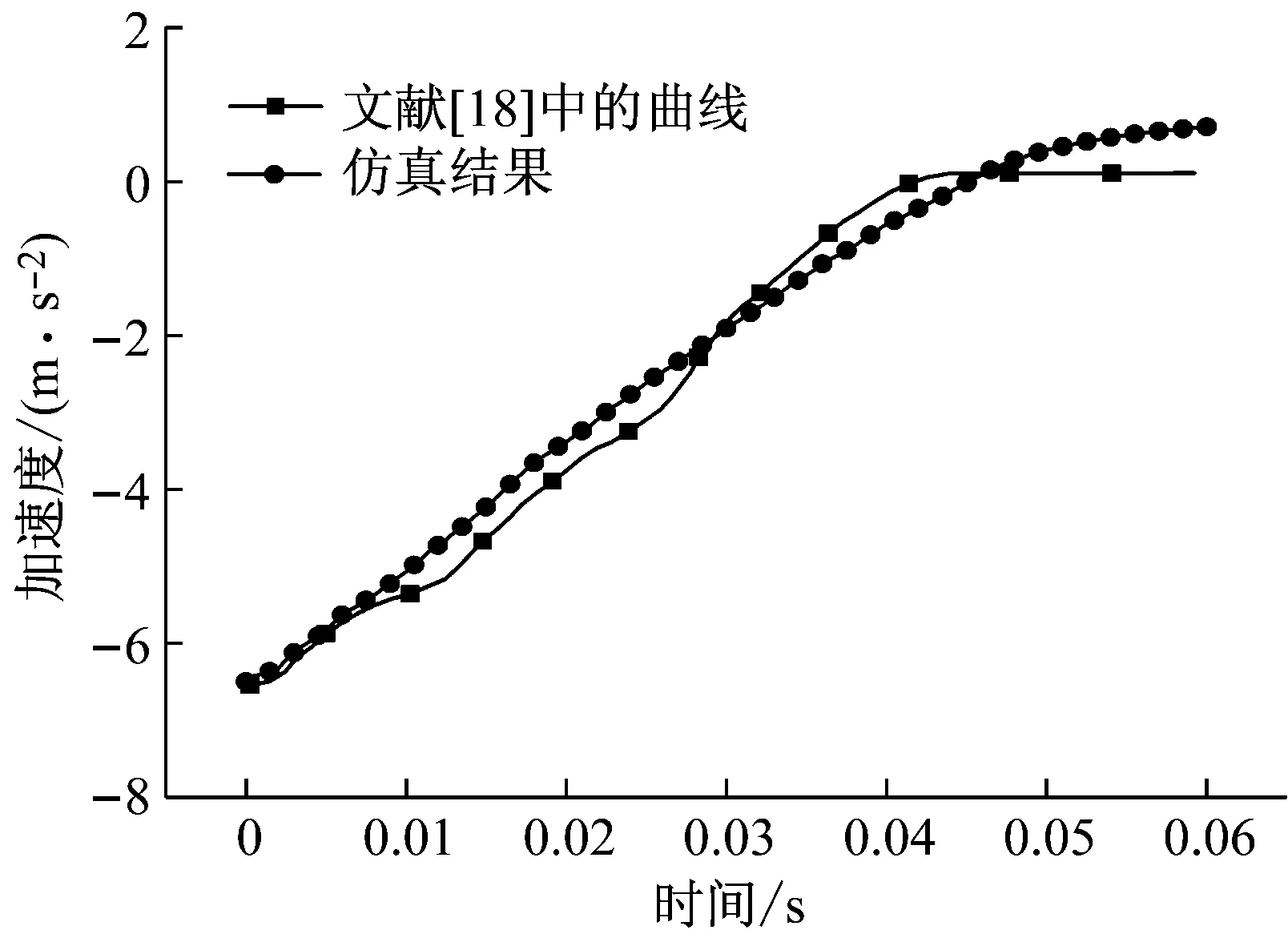
图3 速度-时间曲线

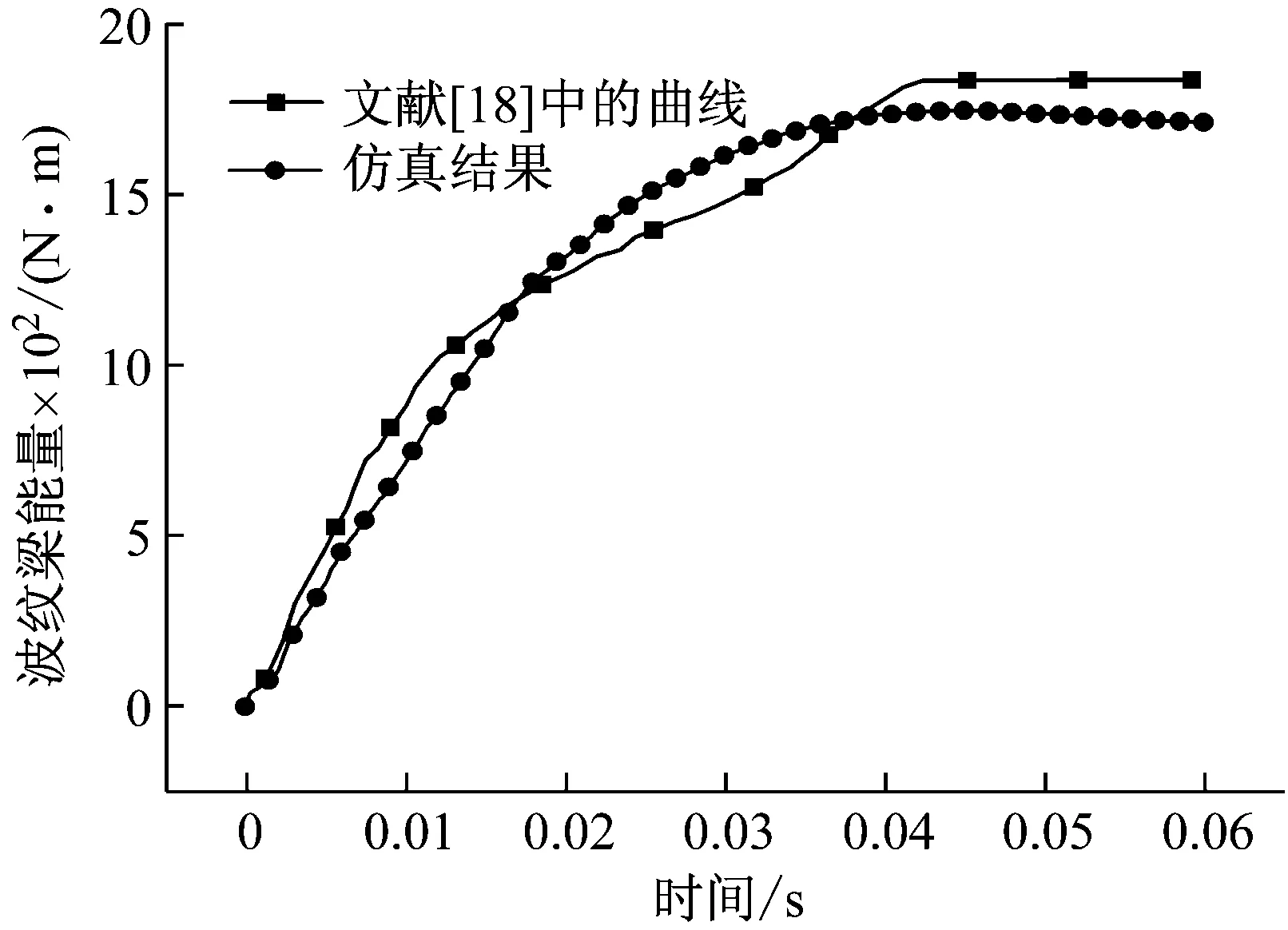
图4 波纹梁能量-时间曲线

定义Rpp(Ratio of peak acceleration and plateau acceleration)用于表示波纹梁峰值载荷和平台载荷的关系。Rpp等于波纹梁受力变形过程中峰值加速度和平台加速度之比。峰值加速度和平台加速度均由有限元软件输出的加速度-时间曲线获得。而波纹梁的吸能能力则用波纹梁变形过程中的最小剩余长度衡量。最小剩余长度越长，说明波纹梁的吸能能力越强。这是因为当波纹梁腹板两薄弱环节之间的部分发生变形时，加速度会在一个特定值附近上下波动，即这段结构的能量吸收能力可以看做是均匀分布的。在对带有褶皱薄弱环节的波纹梁的吸能能力进行对比时，各波纹梁的长度相同，即集中质量相同，结构质量相比于集中质量很小，故波纹梁需吸收的初始动能几乎相同。在此前提下，用结构的最小剩余长度衡量波纹梁的吸能能力是可行的。

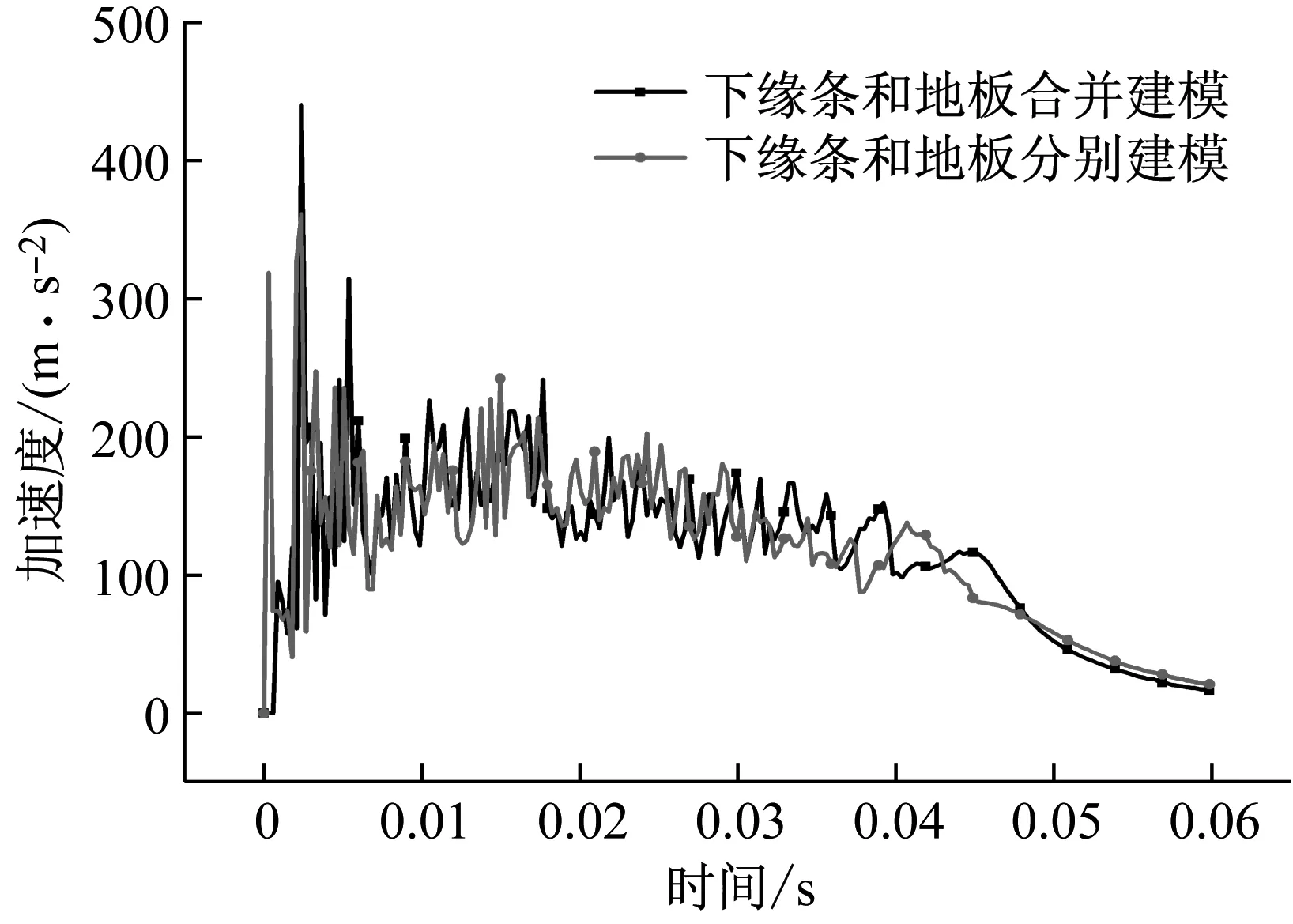
图5 上面板加速度-时间曲线

可以看出，用本文模型仿真得到的曲线和文献[18]中的曲线吻合得较好，但仿真所得的最终速度不为0，而是与初速度方向相反的一个小值。这是由于材料的弹性势能释放导致的上面板回弹。0.06 s内回弹速度峰值为0.72 m/s，回弹高度为7.1 mm，回弹的影响很小，可忽略不计。仿真得到的波纹梁能量与原文也有一定的差异，但差异不大。本文的有限元模型可以代表波纹梁的性能。

上面板的加速度曲线如图5所示。从图中可以看出，在该几何参数下加速度-时间曲线有多个峰值，其中第一个峰值出现在波纹梁刚与地面(下面板)接触时，而最大的峰值出现在薄弱环节完全破坏的时刻。故薄弱环节的设置需满足一定的要求。薄弱环节太强，则过载太大，会导致人员受伤或死亡；薄弱环节太弱，结构强度过低，且会导致多个峰值的产生，仍会产生过大的过载。最理想的薄弱环节能够使Rpp接近于1，即峰值载荷和平台载荷基本保持一致。

峰值加速度过后，加速度-时间曲线进入平台段，加速度在一特定值附近上下波动，且波动幅度越来越小，直到波纹梁被完全压溃或上面板速度降为0。若波纹梁被压溃，则在上下面板接触时会产生另一个峰值加速度，且加速度很大；若速度降为0，则加速度由波纹梁弹性势能的释放产生，当弹性势能完全释放后，加速度由重力产生。考虑到峰值加速度过后，加速度(载荷)的峰值意义不大，而其平均值的大小反映了速度变化速率，进而在一定程度上反映了结构的吸能速率，故可采用平台段加速度均值代表平台段的加速度，并近似认为加速度保持不变。

2.4带有褶皱薄弱环节的正弦波纹梁分析结果

本文设计了A=15 mm，S=5 mm，λ=40°，H=35 mm，L=120 mm，D=160 mm的带褶皱薄弱环节的正弦波纹梁。波纹梁压缩过程中的变形图如图6所示，图中红色区域的应力较大，图6(a)为波纹梁刚与地面发生接触；图6(b)为上薄弱环节发生破坏；图6(c)为下薄弱环节发生破坏；此时上薄弱环节已经基本压溃；图6(d)为下薄弱环节压溃；图6(e)为波纹腹板主体部分开始逐渐压溃；图6(f)为上面板速度下降至0 m/s时的波纹梁状态。文献[18]中带圆弧薄弱段的波纹梁、无薄弱环节的波纹梁及带褶皱薄弱环节的波纹梁的上面板的加速度-时间曲线与如图7所示。可见，加入了褶皱薄弱环节后，波纹梁的峰值加速度下降，峰值加速度和平台加速度基本保持一致。褶皱薄弱环节实现了峰值载荷和平台载荷之间的最理想配置。

(a)

(b)

(c)

(d)

(e)

(f)

图7 带有三种不同薄弱环节的波纹梁上面板加速度-时间曲线

Fig.7 Acceleration-time curve of the top plate of waved beams with three different kinds of trigger geometry

3 各几何参数对带有褶皱薄弱环节的波纹梁吸能性能的影响

带有褶皱薄弱环节的波纹梁具有6个相互独立的几何参数：H,L,D,S,A,λ。下文将对各几何参数对峰值过载及波纹梁吸能能力的影响进行研究。波纹梁的吸能能力由上面板速度为0时波纹梁的剩余长度来衡量，剩余长度越长，波纹梁吸能能力越好。由于结构限制，本文中D和L不变，只对另四个参数对吸能能力的影响进行研究。

在其它变量不变的前提下，对单个变量取一系列的值，分别建模分析，获得上面板的加速度-时间曲线和位移-时间曲线。从上面板的加速度-时间曲线中读取最大加速度和平台加速度；从上面板的位移-时间曲线中获得上面板最大位移，波纹梁总高D与最大位移之差就是波纹梁的剩余长度。

3.1高度H的影响

随H的变化，峰值加速度的变化如图8所示，Rpp的变化如图9所示，剩余长度的变化如图10所示。

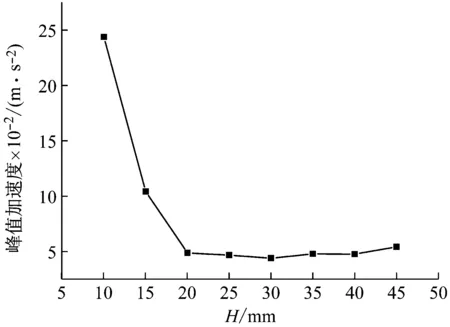
图8 峰值加速度-H曲线

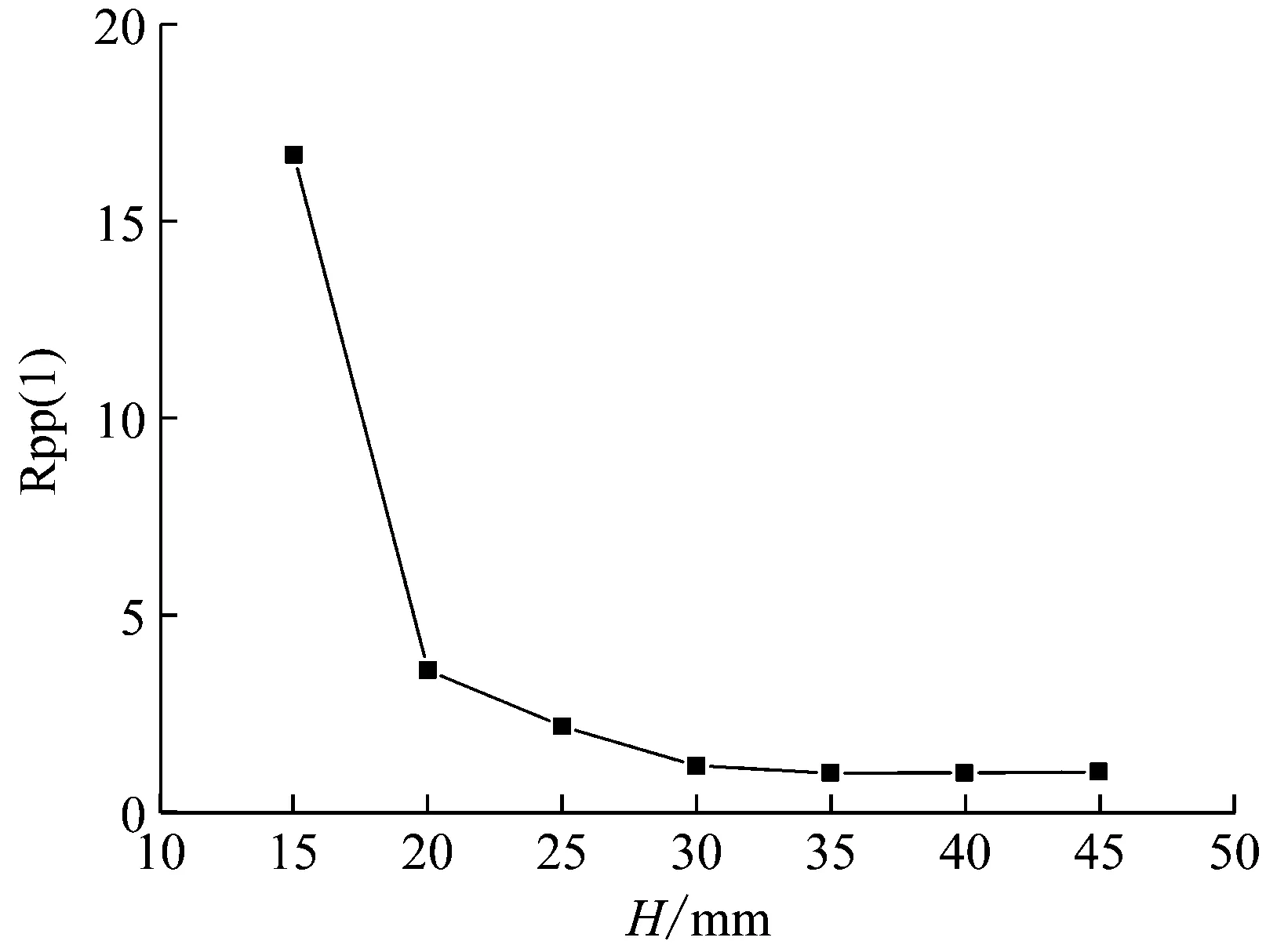
图9 Rpp-H曲线

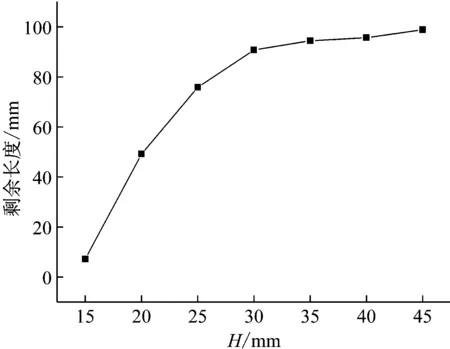
图10 剩余长度-H曲线

从图中可以看出，随着H的增大，峰值加速度在下降，Rpp在下降，而波纹梁的吸能能力在上升。不过H>20 mm后，H变化对峰值加速度影响较小，H>30 mm后，H变化对Rpp和波纹梁剩余长度的影响很小，可以忽略。考虑到增大H会增加结构质量，且需要更大的空间，故H=30 mm相对更优。

当H较小时，波纹梁剩余长度很短。这是由于H较小时，波纹梁将以整体屈曲的方式破坏，H足够大后，波纹梁才具有足够的横向稳定性，结构破坏模式变为局部压溃，吸能能力大幅度上升，平台过载提升，薄弱段得以发挥作用，峰值载荷下降。故随着H的增大，Rpp下降，波纹梁的吸能能力上升。当H继续增大时，初始峰值过载已经低于平台过载，最大加速度出现在平台的前缘，H的变化对平台过载的影响很小。故H的变化对Rpp和剩余长度的影响都很小。

3.2S的影响

对S不同的模型进行分析计算发现：随S的变化，峰值加速度的变化范围在441.1 m/s2到463.8 m/s2之间，Rpp的变化范围在1.15～1.31之间，剩余长度的变化范围在90.14 mm～91.86 mm之间。说明S的变化对峰值加速度、Rpp和剩余长度都没有太大的影响。

3.3A和λ的影响

随A的变化，峰值加速度的变化如图11所示，Rpp的变化如图12所示，剩余长度的变化范围在81.6 mm到92.1 mm之间，变化幅度不大，说明A对吸能性能的影响较小。

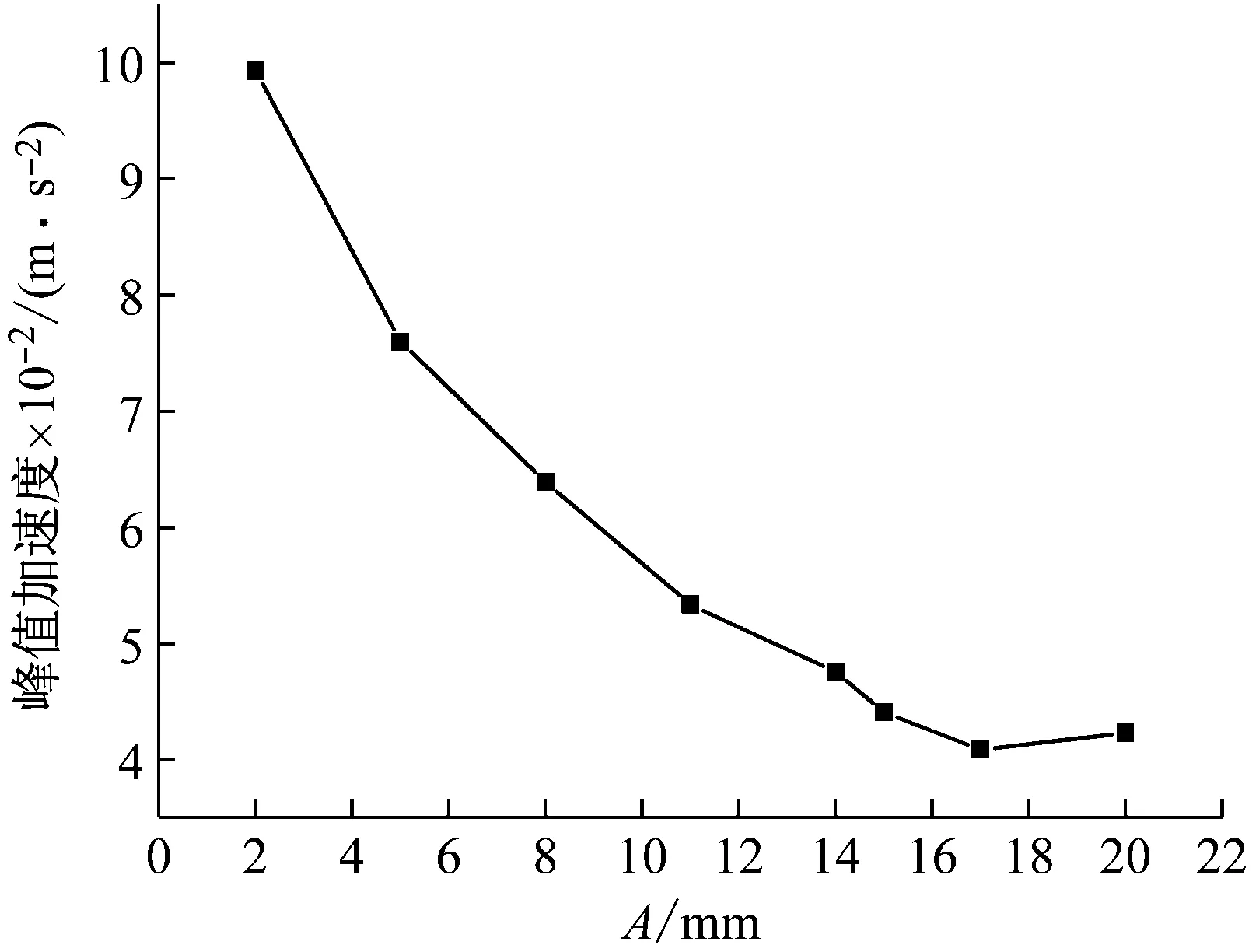
图11 峰值加速度-A曲线

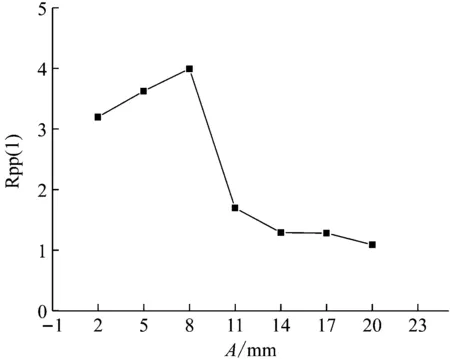
图12 Rpp-A曲线

从图11中可以看出，峰值加速度随A的增大而减小。在A=14 mm后，峰值加速度就基本不随A的变化而变化。从图12中可以看出，A<8 mm时，褶皱段并没有起到应有的作用。而A=11 mm之后，褶皱段起到了缓冲的作用，Rpp值下降很明显。当A≥14 mm之后，Rpp基本不随A变化而变化。考虑到A的增大会增加结构质量，A=14 mm相对较优。

随λ的变化，峰值加速度的变化如图13所示，Rpp的变化如图14所示，剩余长度的变化范围在83.1 mm到92.1 mm之间，变化幅度不大，说明λ对吸能性能的影响较小。图中λ的下限为30°，这是因为更小的角度会导致参数化建模过程中网格质量过差，甚至出现三角形单元，以至于无法进行有限元分析。

从图13中可以看出，峰值加速度随λ的增加而增加。但λ<40°的时候，峰值加速度的变化很小，可以忽略。

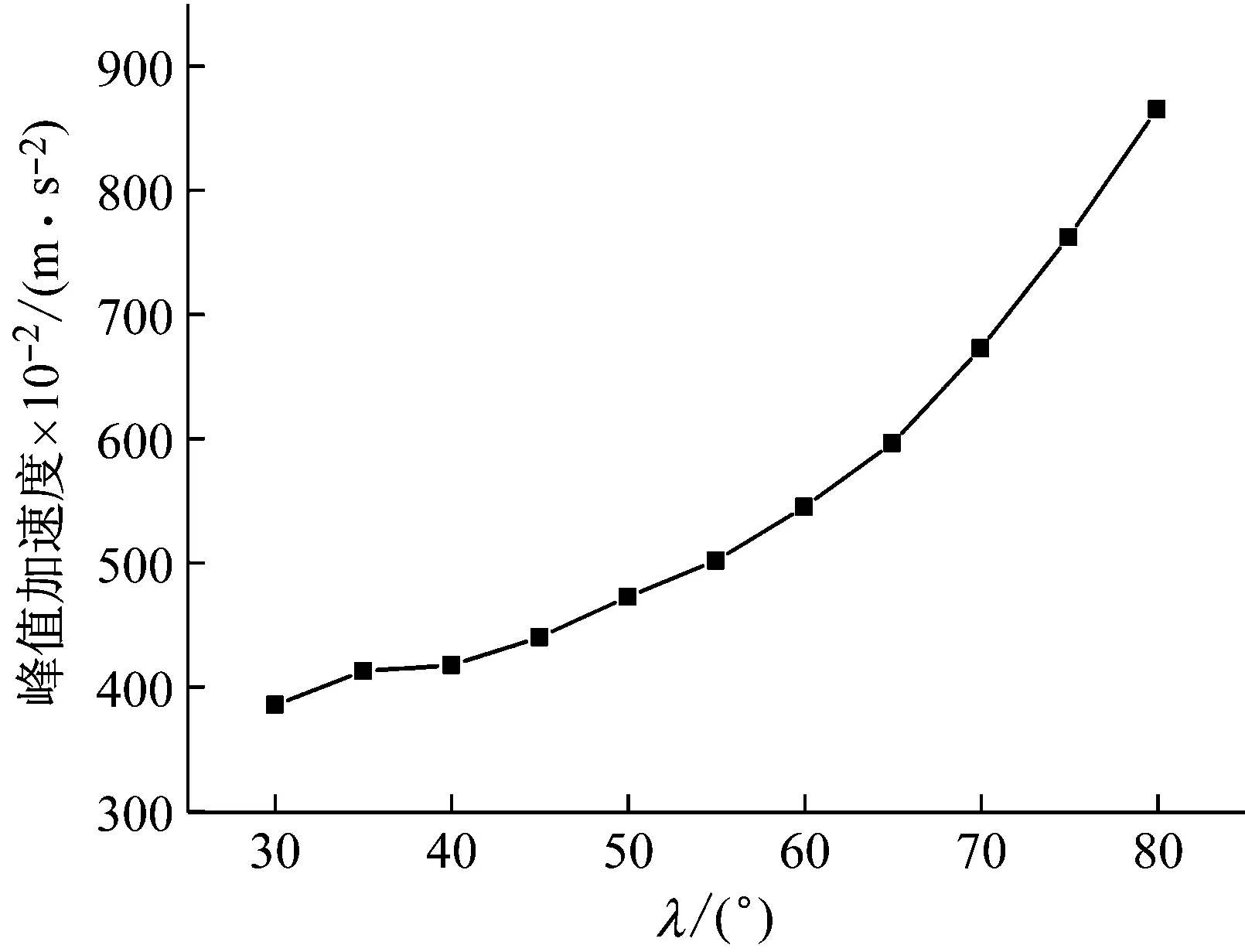
图13 峰值加速度-λ曲线

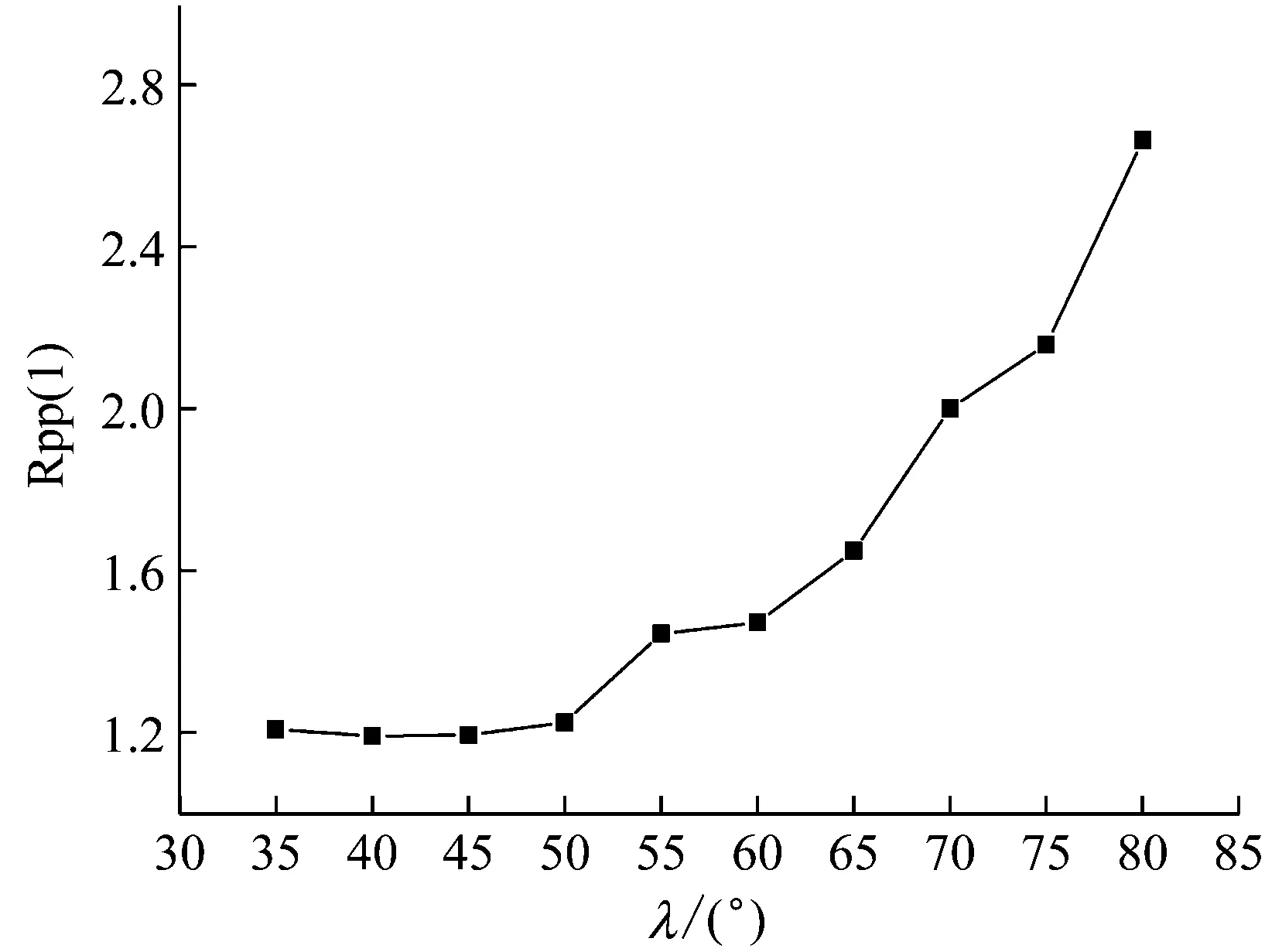
图14 Rpp-λ曲线

从图14中可以看出，当λ<50°的时候，Rpp基本不随λ变化而变化。但λ>50°之后，Rpp随λ增大而增大，说明λ<50°相对较优。

Rpp随Acos(λ)的变化如图15所示。由于A<11 mm时褶皱段并没有起到应有的作用，图15中并没有加入这三组数据。从图中可以看出，Rpp基本上随着Acos(λ)的增大而减小，直到降到1左右为止。这是由于随着Acos(λ)的增大，轴力引起的弯矩也在增大，从而导致轴向附加应力的增加。也就是说，Acos(λ)越大，褶皱段承载能力的削弱也就越多。当初始峰值过载低于平台段的最大过载时(Acos(λ)>10.6 mm)，Rpp接近于最小值1。此时Acos(λ)的变化对Rpp的影响不大。

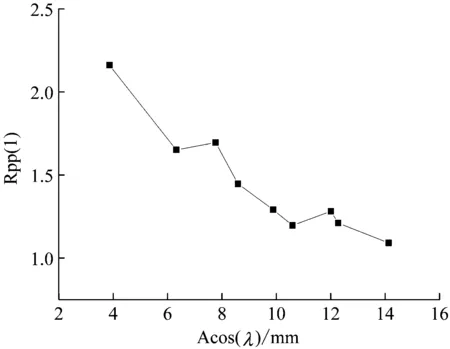
图15 Rpp-Acos(λ)曲线

需注意的是，Acos(λ)的最优取值需考虑A和λ的最优取值范围，只有A和λ都在其最优取值范围内时，Acos(λ)=10.6 mm最优才是正确的。若A过大而r过小，会导致褶皱段强度太小，褶皱段结构强度过低，褶皱段破坏后剩余的结构会产生很大的第二峰值，仍会产生过大的过载。

此外，褶皱段的几何参数均未对剩余强度产生很大的影响，说明加入褶皱薄弱环节不会对波纹梁的吸能性能产生很大的削弱。这也是褶皱薄弱环节的一个优势。

4 总 结

(1) 建立了带有褶皱薄弱环节的正弦波纹梁压缩吸能有限元模型。模型分析结果与论文[18]中的结果相符。褶皱薄弱环节能够使波纹梁的峰值载荷和平台载荷基本保持一致。

(2) 将带有褶皱薄弱环节的正弦波纹梁各几何参数对其吸能能力的影响进行了研究。峰值载荷随H、A的增大而减小，随λ的增大而增大。Rpp随H的增大而减小，随Acos(λ)的增大而减小。而波纹梁剩余长度基本上只与H有关。褶皱薄弱段对波纹梁的吸能性能的影响较小。

(3)S的变化对波纹梁吸能性能和Rpp的影响都很小，说明褶皱薄弱环节的位置并不重要。

(4) 最优的H=30 mm，最优的A=15 mm，λ应不大于40°，最优的Acos(λ)=10.6 mm。

[1] LAVOIE J A, MORTON J. Design and application of a quasistatic crush test fixture for investigating scale effects in energy absorbing composite plates[R]. NASA Contractor Report 4526, Washington, D.C: National Aeronautics and Space Administration, 1993.

[2] BARK L W, YANIV G. Cost-effective production of helicopter energy-absorbing subfloor structures with advanced thermoplastic composites.[C]// The American Helicopter Society 49th Annual Forum, St. Louis: American Helicopter Society International, 1993: 519-529.

[3] AIAA. Simulating composites crush and crash events using abaqus[R]// AIAA, 50th Aiaa/asme/asce/ahs/ asc Structures, Structural Dynamics and Materials Conference, California: AIAA, 2009: 1-12.

[4] NAGEL G M, THAMBIRATNAM D P. A numerical study on the impact response and energy absorption of tapered thin-walled tubes[J]. International Journal of Mechanical Sciences, 2004, 46(2): 201-216.

[5] SANTOSA S, BANHART J, WIERZBICKI T. Experimental and numerical analyses of bending of foam-filled sections[J]. Acta Mechanica, 2001, 148(1): 199-213.

[6] TAN X C, CHEN X G. Modelling energy absorption in textile composite cellular structures[C]// AIAA, 49th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics and Materials Conference., Illinois: AIAA, 2008: 1-12.

[7] 倪先平,王永亮,荚淑萍,等. 直升机机身下部复合材料典型结构耐坠特性研究[J]. 复合材料学报, 2003, 20(4): 51-57.

NI Xianping, WANG Yongliang, JIA Shuping, et al. Analysis of crash impact behaviour of typical composite components of helicopter bottom structure[J]. Acta Materiae Compositae Sinica, 2003, 20(4): 51-57.

[8] 印春伟,徐建,童明波. 复合材料的应用对波纹梁吸能能力的改进分析[J]. 江苏航空, 2012(增刊1): 130-132.

YIN Chunwei, XU Jian, TONG Mingbo. Analysis of the improvement of energy absroption capability of waved beams with the application of composite materials[J]. Jiangsu Aviation, 2012(Sup1): 130-132.

[9] ZHOU W Z, CRAIG J, HANAGUD S. Crashworthy behavior of graphite/epoxy composite sine wave webs[C]// SDMC Aiaa/Asme/Asce/Ahs/ Asc Structures, 32nd AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics and Materials Conference, Reston: AIAA, 1991: 1618-1626.

[10] AIAA. A method of predicting the energy-absorption capability of composite subfloor beams[J]. Journal of the American Helicopter Society, 1987, 34(2): 63-67.

[11] 刘豫,李巧,宋艳华. 大尺寸复合材料RTM波纹梁设计优化[J]. 航空工程进展, 2014(4): 541-546.

LIU Yu, LI Qiao, SONG Yanhua. Optimal design of composite RTM waved-beams with large size[J]. Advances in Aeronautical Science and Engineering, 2014(4): 541-546.

[12] 孟祥吉,燕瑛,罗海波, 等. 复合材料波纹梁冲击试验与数值模拟[J]. 复合材料学报, 2015, 32(1): 196-203.

MENG XiangJi, YAN Ying, LUO Haibo, et al. Impact tests and numerical simulation of composite waved-beam[J]. Acta Materiae Compositae Sinica, 2015, 32(1): 196-203.

[13] 冯振宇,袁鹏,邹田春,等. 不同波纹梁结构吸能特性仿真分析[J]. 机械科学与技术, 2014, 33(6): 948-952.

FENG Zhenyu, YUAN Peng, ZOU Tianchun, et al. Simulation analysis of energy absorption characteristics for different waved beams[J]. Mechanical Science and Technology for Aerospace Engineering, 2014, 33(6): 948-952.

[14] 卢致龙, 王新峰. 基于Hashin准则的直升机复合材料波纹梁耐撞性分析[J]. 直升机技术, 2015(1): 25-38.

LU Zhilong, WANG Xinfeng. Criteria crashworthness analyses of helicopter composite waved beams based on Hashin[J]. Helicopter Technique, 2015(1): 25-28.

[15] 卢致龙, 常成. 直升机复合材料波纹梁结构抗坠毁设计技术研究[J]. 直升机技术, 2015(3): 14-19.

LU Zhilong, CHANG Cheng. Study of helicopter composite wave beam structure anti-crash design technology[J]. Helicopter Technique, 2015(3): 14-19.

[16] 郑建强,向锦武,罗漳平,等. 民机机身耐撞性设计的波纹板布局[J]. 航空学报, 2010, 31(7): 1396-1402.

ZHENG Jianqiang, XIANG Jinwu, LUO Zhangping, et al. Crashworthiness layout of civil aircraft using waved-plate for energy absorption[J].Acta Aeronautica et Astronautica Sinica, 2010, 31(7): 1396-1402.

[17] 刘瑞同,王鑫伟,荚淑萍. 碳纤维-环氧树脂波纹梁吸能能力的试验研究[J]. 航空学报, 2002, 23(1): 59-61.

LIU Ruitong, WANG Xinwei, JIA Shuping. Experimental study on energy absorption of carbon-epoxy waved beams[J]. Acta AERONAUTICA ET Astro-Nautica Sinica, 2002, 23(1): 59-61.

[18] 龚俊杰, 王鑫伟. 薄弱环节对复合材料波纹梁吸能能力的影响[J]. 材料工程, 2006(5): 28-31.

GONG Junjie, WANG Xinwei. Effect of trigger geometry on energy absorption of composite waved beams[J]. Journal of Materials Engineering, 2006(5): 28-31.

[19] 龚俊杰, 王鑫伟. 复合材料波纹梁吸能能力的数值模拟[J]. 航空学报, 2005, 26(3): 298-302.

GONG Junjie, WANG Xinwei. Numerical simulation of energy absorption capability of composite waved beams[J]. Acta Aeronautica et Astro-nautica Sinica, 2005, 26(3): 298-302.

[20] 龚俊杰, 王鑫伟. 复合材料波纹梁盒段耐撞性的数值模拟[J]. 应用力学学报, 2007, 24(1): 165-168.

GONG Junjie, WANG Xinwei. Numerical simulation to crashworthness of composite corrugated board boxes[J]. Chinese Journal of Applied Mechanics, 2007, 24(1): 165-168.

Energyabsorptioncapabilityofasinewavedbeamwithafoldedweaksegment

ZHOU Huazhi， WANG Zhijin， HAN Wei， JIANG Binbin

(National Defense Key Lab of Advanced Aircraft Design Technology, Nanjing University of Aeronautics and Astronautics, Nanjing 210016, China)

A weak segment has a large influence on the energy absorption capacity of waved beams. Reasonable design of a weak segment can reduce the impact overload of waved beams to decrease overload delivered from a structure to crews inside, and make a waved beam buckled steadily to absorb more energy. Here, the concept of a folded weak segment for a waved beam was proposed, the energy absorption properties of a waved beam with a folded weak segment were studied. Firstly, the FE simulation of a waved beam with an arc shape weak segment was done and the correctness of the FE simulation was verified. Then the FE model for a sine waved beam with a folded weak segment was established, the effects of geometric parameters of the waved beam on its energy absorbing property and its maximum acceleration during the beam suffering crash impact were studied. The results showed that the folded weak segment can effectively reduce the maximum impact load of the waved beam, its effect on the energy absorption ability of the waved beam is small. The results provided a guide for the application of waved beams in energy-absorbing structures.

waved beams; crashworthiness; energy absorption; weak segment; geometric parameter

江苏省普通高校研究生科研创新计划资助项目(KYLX_0298);江苏高校优势学科建设工程基金

2016-08-12 修改稿收到日期：2016-11-02

周华志 男，博士，1989年9月生

王志瑾 女，博士，博士生导师，1963年7月生

V214.3

： A

10.13465/j.cnki.jvs.2017.17.036