附设黏滞阻尼器的仿古建筑混凝土枋-柱节点动力性能试验研究

薛建阳， 董金爽， 隋 龑， 戚亮杰， 许 丹

(西安建筑科技大学 土木工程学院，西安 710055)

附设黏滞阻尼器的仿古建筑混凝土枋-柱节点动力性能试验研究

薛建阳， 董金爽， 隋 龑， 戚亮杰， 许 丹

(西安建筑科技大学 土木工程学院，西安 710055)

为研究附设黏滞阻尼器的仿古建筑混凝土枋-柱节点在地震作用下的抗震性能，设计制作了3个仿古建筑混凝土枋-柱节点，包括2个附设黏滞阻尼器的有控结构试件，1个未附设黏滞阻尼器的无控结构对比试件，对其进行动力试验。观察试件的受力过程及破坏特征，分析其受力机理及破坏模式，并研究了其荷载-位移滞回曲线、骨架曲线、承载能力、刚度退化等力学特性。试验结果表明：附设黏滞阻尼器的仿古建筑混凝土枋-柱节点抵御外荷载的能力明显高于未附设黏滞阻尼器的无控结构，屈服荷载提高幅度平均值约为27.4%，极限荷载提高幅度平均值约为22.4%；附设阻尼器的有控结构位移延性及耗能能力均优于无控结构，且有控结构的骨架曲线在达到极限荷载之后的下降段更为平缓；极限荷载时，有控结构的等效黏滞阻尼系数提高幅度约为27.3%～30.8%，说明附设黏滞阻尼器的仿古建筑混凝土枋-柱节点具有更为优越的抗震性能。

仿古建筑；混凝土；动力试验；抗震性能；黏滞阻尼器

仿古建筑作为中华民族建筑风格与地域建筑特色方面的传承载体，是具有良好推广应用前景的探索与创新，对目前我国城市发展、建设具有重要的意义。

当前对仿古建筑的研究还处于起步阶段。薛建阳等[1]进行了传统风格建筑钢结构梁-柱节点试验研究；高延安等[2]对环境激励下古建筑飞云楼动力性能进行了分析研究，在不损伤古建结构性能条件下获得了结构自振频率、阻尼等模态参数；谢启芳等[3]进行的混凝土仿古建筑试验表明，其耗能系数和延性系数小于现代常规结构，很难满足结构抗震设计的要求。因此如何确保仿古建筑在地震作用下的力学性能，成为仿古建筑研究亟待解决的关键性技术问题。

传统抗震体系把结构构件作为耗能部件，通过容许结构构件在地震中产生塑性变形来吸收地震能量，而消能减震结构将地震能量引向特别设置的阻尼装置加以吸收耗散，使主体结构尽可能处于弹性阶段或弹塑性阶段，从而保护结构的安全。1990年Constantinou等[4]开始研制应用于土木工程领域的黏滞阻尼器；西雅图棒球场安装了36个黏滞阻尼器，用于风振和屋盖开合时的振动控制；日本Shibuya Park Road大楼采用10个黏滞阻尼器来耗散输入的地震能量；北京饭店、北京展览馆由于按当时抗震规范进行设计，其抗震性能较差，为满足目前的抗震设防要求，采用黏滞阻尼器进行加固，取得了良好的效果[5]。

目前，将黏滞阻尼器应用于仿古建筑混凝土枋-柱节点的应用研究尚未见报道，因此对混凝土仿古建筑关键部位附设黏滞阻尼器后的结构抗震性能进行研究，不但可以填补仿古建筑结构设计理论与方法的空白，也为工程实际提供科学的参考依据，具有重大的理论意义和工程应用价值。

鉴于此，本课题组设计了3个仿古建筑混凝土枋-柱节点，包括2个附设黏滞阻尼器的仿古建筑混凝土枋-柱节点的有控结构，1个未附设黏滞阻尼器的无控结构对比试件。采用动力加载方式，对其破坏模式、受力机理及抗震性能进行试验研究，为工程设计提供理论基础。

1 试验设计

1.1试件设计

试验设计了3个仿古建筑混凝土枋-柱节点，试件编号分别为SLJ-1～SLJ-3，其中SLJ-1试件为未布置阻尼器的无控结构对比试件。试件以某佛学院大雄宝殿为原型，并依照清《工程做法则例》[6]材份换算，试件总高2 650 mm，总宽3 000 mm。

试件上柱为方钢管混凝土结构，下柱及枋为普通钢筋混凝土结构，方钢管截面尺寸为160 mm×5.5 mm，试件几何尺寸及截面配筋如图1示，试件按照“强柱弱梁、强剪弱弯、强节点弱构件”的抗震设防要求进行设计。实测与试件同龄期混凝土立方体抗压强度平均值fcu=58.2 MPa。钢筋力学性能指标如表1所示。设计轴压比n=0.25。

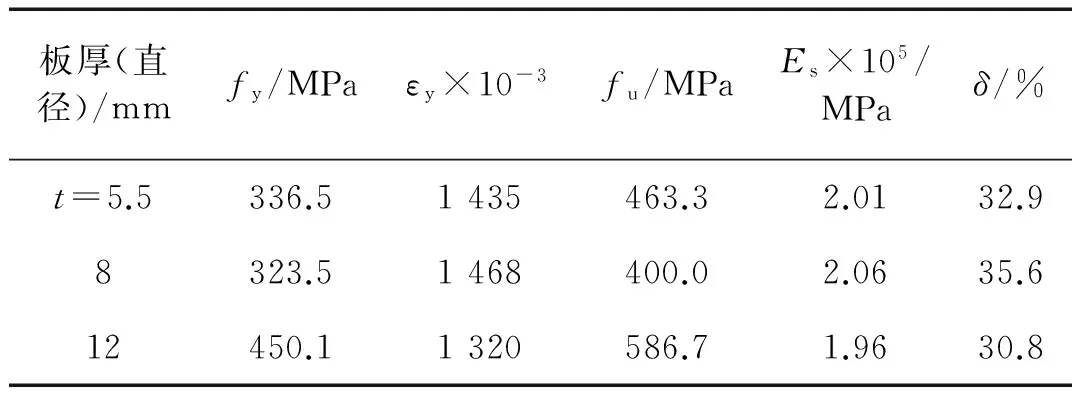
表1 钢材材性指标

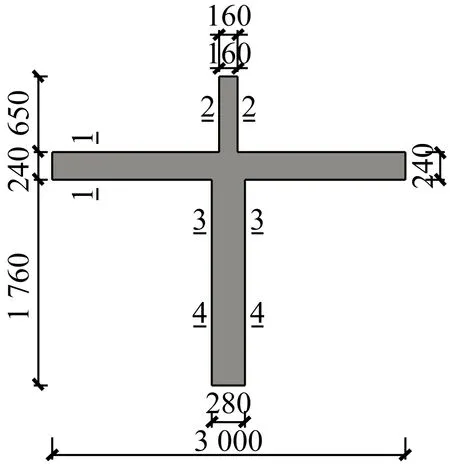
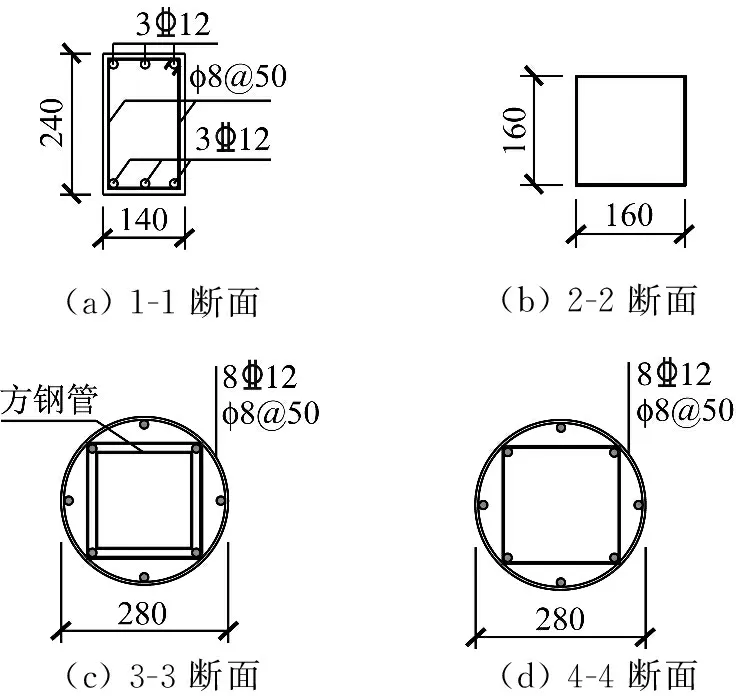
(a)1-1断面(b)2-2断面(c)3-3断面(d)4-4断面

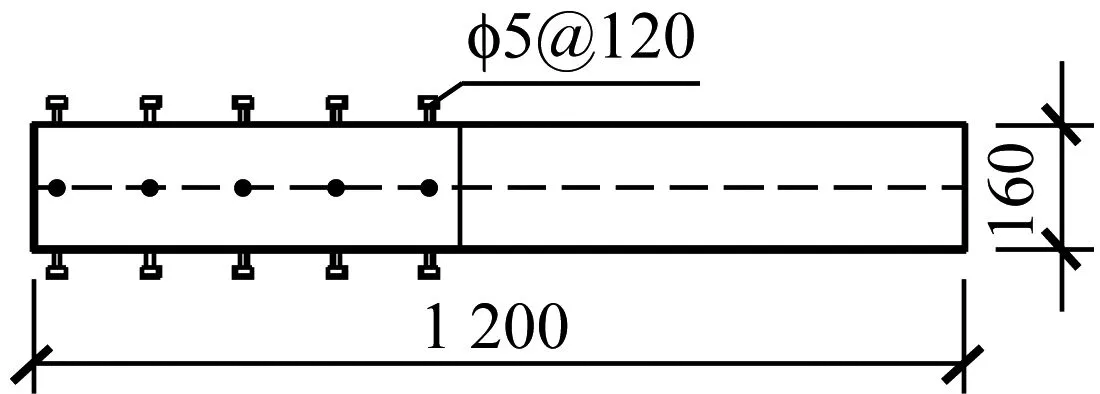
(e) 方钢管

1.2黏滞阻尼器选用

选用速度相关型黏滞阻尼器，该类型阻尼器通过调整内部黏滞流体的黏度及流速控制可阻尼器阻尼力与阻尼器两端相对速度的不同次方成正比。

黏滞阻尼器计算公式如式(1)所示[7]。

F=CVα

(1)

式中：C为阻尼系数;V为活塞运动的相对速度;α为阻尼指数;α为1时，为线性阻尼器，其他(α≠1)为非线性阻尼器。

本次试验选用非线性(α≠1)黏滞阻尼器，设计参数如表2所示。具体形式如图2所示。

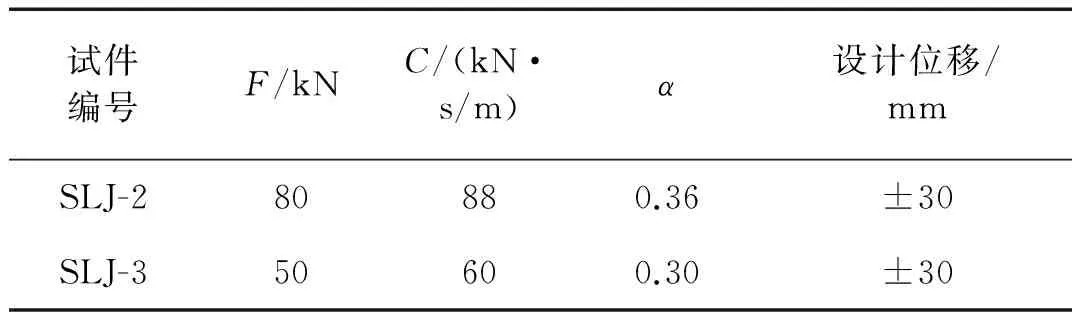
表2 黏滞阻尼器设计参数

黏滞阻尼器安装方法：预先在阻尼器设计安装位置预埋钢板，预埋钢板的长度和宽度比阻尼器支座大100 mm，预埋钢板应焊接足够多的锚固钢筋深入到构件内，如图2(a)示，采用对称断续焊接方式将预埋钢板与阻尼器支座周边焊接牢固，而后，将黏滞阻尼器两端置于支座双耳内，插入螺栓并拧紧。阻尼器支座如图3所示。

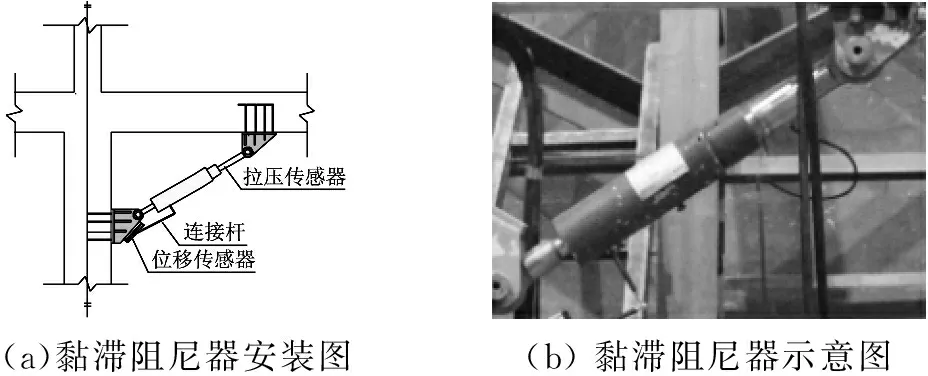
(a)黏滞阻尼器安装图(b)黏滞阻尼器示意图

图2 黏滞阻尼器

Fig.2 Installation drawing and sketch of viscous damper

图3 黏滞阻尼器支座

1.3加载方案

试验加载装置如图3所示，枋端采用单向铰支座控制，使其只可以在水平方向移动，上柱柱端通过MTS793电液伺服程控结构试验系统加载，位移行程为500 mm(±250 mm)，采用1 000 kN千斤顶在柱顶施加轴向荷载，千斤顶与反力梁之间设置滚轮装置，使千斤顶能够随柱顶实时水平移动。

试验的基本过程为：首先调整柱顶的千斤顶，使节点试件处于轴心受压状态，并施加轴向荷载至设计值，然后在上柱柱端按照预先设定好的加载制度通过MTS系统施加荷载。

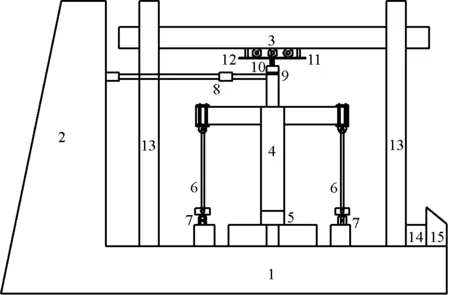
1.基座 2.反力墙 3.加载架 4.试件 5.柱底铰支座 6.连接器 7.单向铰支座 8.液压伺服作动器 9.垫块 10.千斤顶 11.钢板 12.滚珠 13.支架 14.支撑钢架

图4 试验加载装置图

Fig.4 Test setup

试件破坏标志为：水平荷载降至最大承载力85%以下，或层间位移角超限，终止试验。

1.4加载制度

试验采用动力加载制度，正弦波加载形式，通过MTS793电液伺服程控结构试验系统输入正弦波频率及振幅。输入的振幅及频率由《建筑抗震设计规范》(GB50011—2010)[8]及《中国地震烈度表》(GB/T 17742—2008)[9]中相关数据确定。加载频率主要是根据不同加载工况下正弦波荷载的峰值加速度大小反推得出，正弦波加速度的峰值根据地震烈度等级的划分及其对应的水平地震动参数范围作为设计依据。控制位移设计依据是消能减震结构的层间弹塑性位移角限值应符合预期的变形控制要求，宜比非消能减震结构减小。依据美国土木工程学会ASCE进行的黏滞阻尼器力学性能试验报告中所采用的测试参数[10]及《建筑消能阻尼器》(JGT209—2012)[11]制定加载制度的相关参数。

动力加载制度如表3所示。

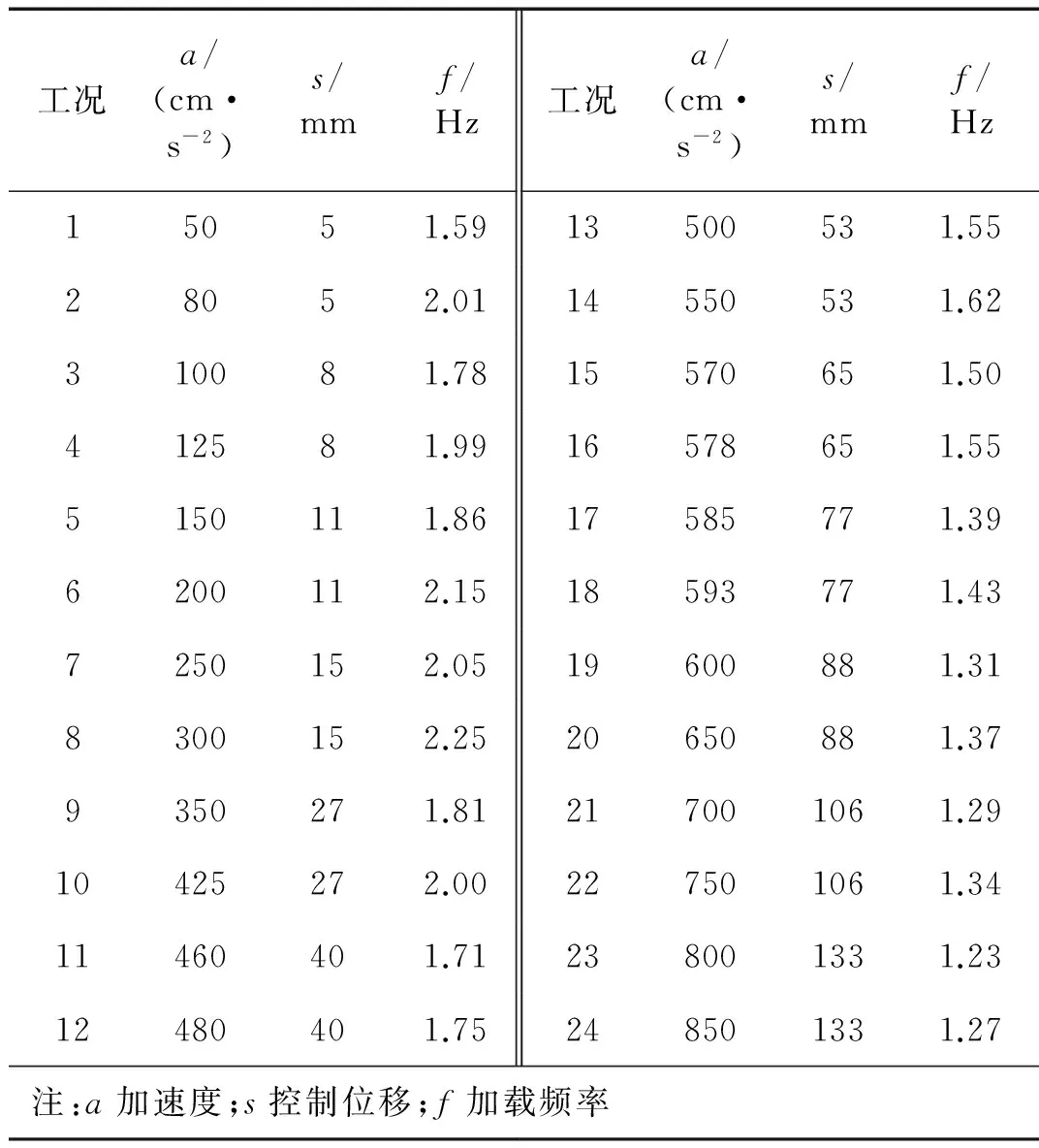
表3 试验加载制度

1.5量测方案

试件主要量测内容为：①节点破坏情况；②枋端塑性铰区域破坏情况及变形情况；③节点核心区箍筋应变及承载力；④枋端纵筋、箍筋应变及承载力；⑤柱顶荷载-位移滞回关系。

应变数据由8通道DC-104R动态应变数据采集仪实时记录，上柱柱端水平荷载-位移关系通过MTS加载系统自动采集。应变片布置如图5所示。

2 试验破坏现象及受力机理分析

2.1加载破坏过程

试件SLJ-1～SLJ-3试验过程及试件破坏现象基本相同，整个加载过程大致可分4个阶段：

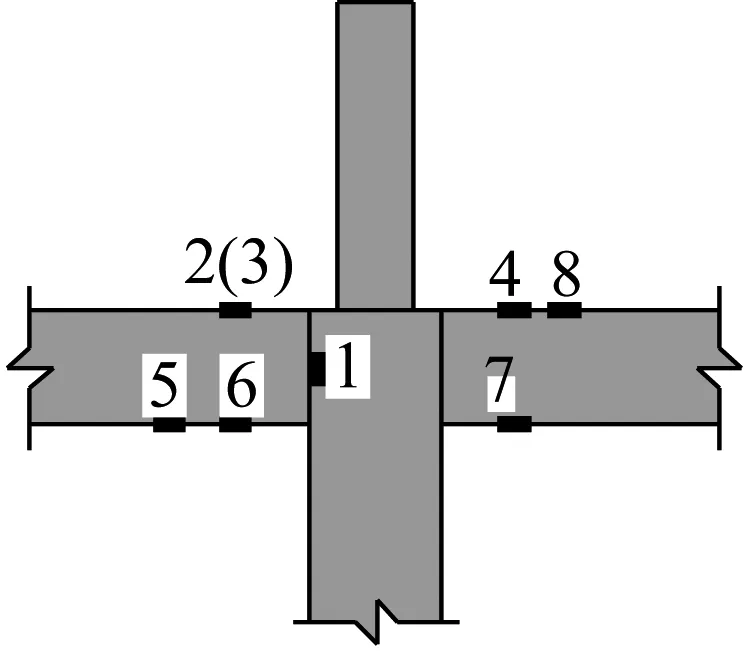
(a) 正视图

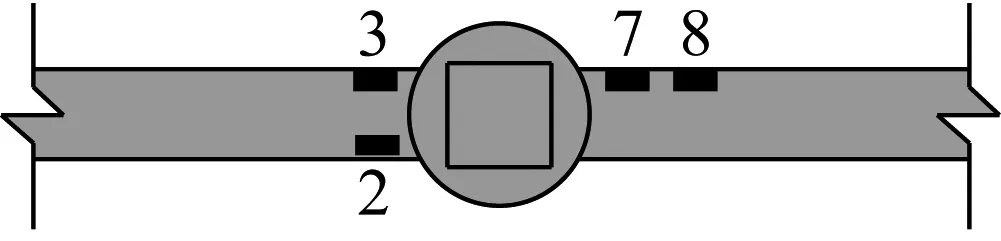
(b) 俯视图

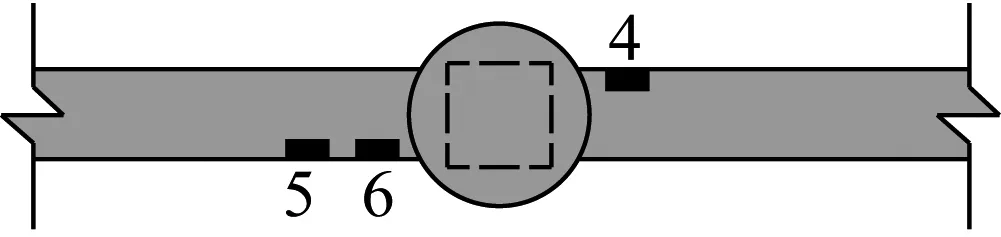
(c) 仰视图

(1) 开裂阶段：竖向荷载加载至预定值后，施加柱端水平荷载，随着水平荷载增大，枋端出现弯曲裂缝。各试件开裂荷载大致相等，表明附设黏滞阻尼器对改善节点抗裂能力不明显；

(2) 屈服阶段：随着柱端水平荷载的继续增大，枋端出现弯剪裂缝，节点核心区两侧裂缝分布大致对称，随着荷载的增大，裂缝继续扩展，并伴随新裂缝的出现。随后，枋端钢筋率先屈服，水平荷载-位移滞回曲线出现明显的拐点，经判断，试件进入弹塑性工作阶段，此时，核心区钢筋仍处于弹性工作阶段；

(3) 极限阶段：试件进入弹塑性阶段后，承载力仍继续增大，直至达到峰值。在该加载过程中，枋端钢筋相继屈服。枋端混凝土局部压碎剥落严重，但未见钢筋裸露。枋端与柱连接区域形成贯通裂缝；

(4) 破坏阶段：水平荷载超过峰值荷载之后，随着水平位移的增大，枋端混凝土压碎剥落区域逐渐扩大，在加载过程中，有明显的混凝土大面积剥落现象，且可见枋端钢筋外露，但核心区均未见明显裂缝。试件SLJ-1在加载的最后几个工况，枋端混凝土已大部分剥落，枋端形成铰接点，不适宜继续加载，且柱顶最大水平荷载已下降至峰值荷载85%以下，试件宣告破坏，终止试验。试件SLJ-2及SLJ-3，加载至最后几个工况，枋端亦是混凝土大部分剥落，钢筋外露，与柱连接处枋端的上顶面、下底面混凝土已完全压碎剥落，形成凹陷，随着加载的继续，该凹陷区域逐渐扩大，最终枋端上顶面混凝土完全剥落，此时，枋端已形成完全铰支座，但黏滞阻尼器作为支撑存在，确保结构继续承载，最终试件因枋端破坏严重，且柱顶最大水平荷载已下降至峰值荷载的85%以下，试件宣告破坏，终止试验。

试件的最终破坏形态如图6所示。

(a) 试件最终破坏形态

(b) SLJ-1枋端混凝土贯通裂缝

(d) SLJ-2混凝土剥落

(e) SLJ-3混凝土剥落、钢筋外露

图6 破坏形态

Fig.6 Failure pattern of specimens

2.2破坏模式分析

对试件最终破坏形态及受力过程进行分析，概述如下：

当荷载较小时，试件处于弹性工作阶段，卸载后无残余变形，其水平荷载-位移滞回曲线基本表现为线性关系，滞回曲线包络面积较小，试件耗能主要是以可恢复的弹性应变能为主；随着荷载的增大，试件裂缝增大增宽，枋端混凝土压碎剥落，钢筋外露，枋端与柱交接处形成贯通裂缝，枋端上下面混凝土压碎剥落尤为严重。对于未附设粘滞阻尼器的试件，当枋端出现塑性铰，继续加载，结构变成可变体系，不适宜继续加载而终止试验；对于附设黏滞阻尼器的试件，枋端形成梁铰机制，而附设的黏滞阻尼器作为支撑，可确保结构继续承载，最终试件因枋端破坏严重，且柱顶最大水平荷载已下降至峰值荷载的85%以下，终止试验。

综上分析，可知，有控结构及无控结构破坏模式主要分为两大类：

(1) 对于无控结构，试件因形成梁铰机制，不适宜继续加载，从而终止试验，试件破坏类型为梁铰破坏机制；

(2) 对于有控结构，试件虽形成梁铰机制，但黏滞阻尼器可作为支撑存在，可确保结构继续承载，试件荷载-位移曲线下降段较平缓,试件破坏为梁铰破坏机制。

3 试验结果及分析

3.1应变分析

以试件SLJ-1、SLJ-2为例，分析仿古建筑混凝土枋-柱节点枋端及核心区应变，研究其节点不同部位应变特点。

选取枋端塑性铰区域电阻应变片2、7及核心区电阻应变片1进行应变分析。各测点荷载-应变曲线如图7、图8所示。

3.1.1 SLJ-1应变分析

试件SLJ-1测点2，其水平荷载-应变曲线如图7(a)、7(b)示，在工况10时最大应变值在630 με以内，小于材料的屈服应变值，卸载后几乎无残余应变，表明试件仍在弹性工作阶段；随着加载的继续，至工况14时，钢筋应变值达到2 300 με，明显超过材料屈服应变值，卸载后存在残余应变，说明试件进入弹塑性工作阶段。

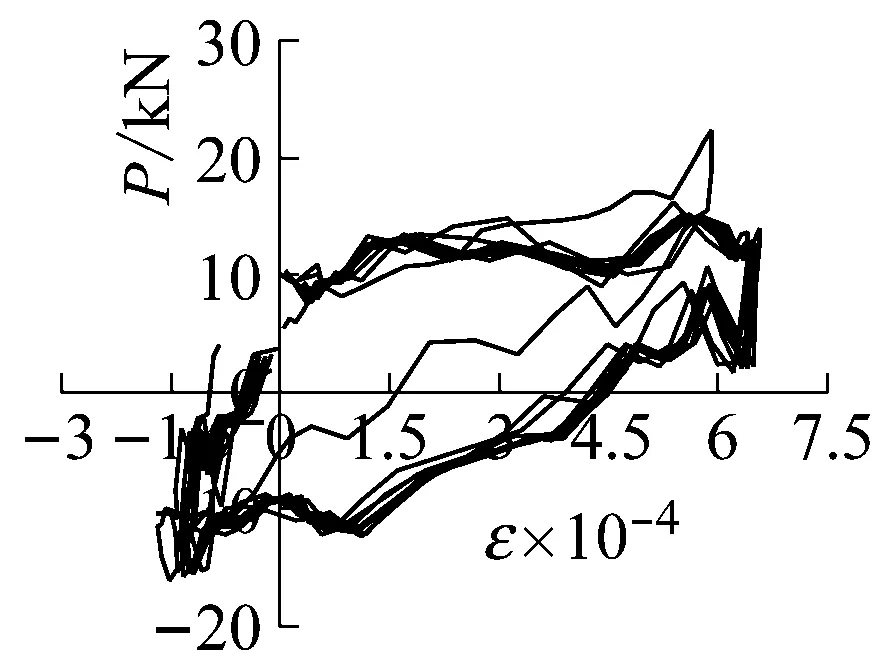
(a) SLJ-1测点2工况10

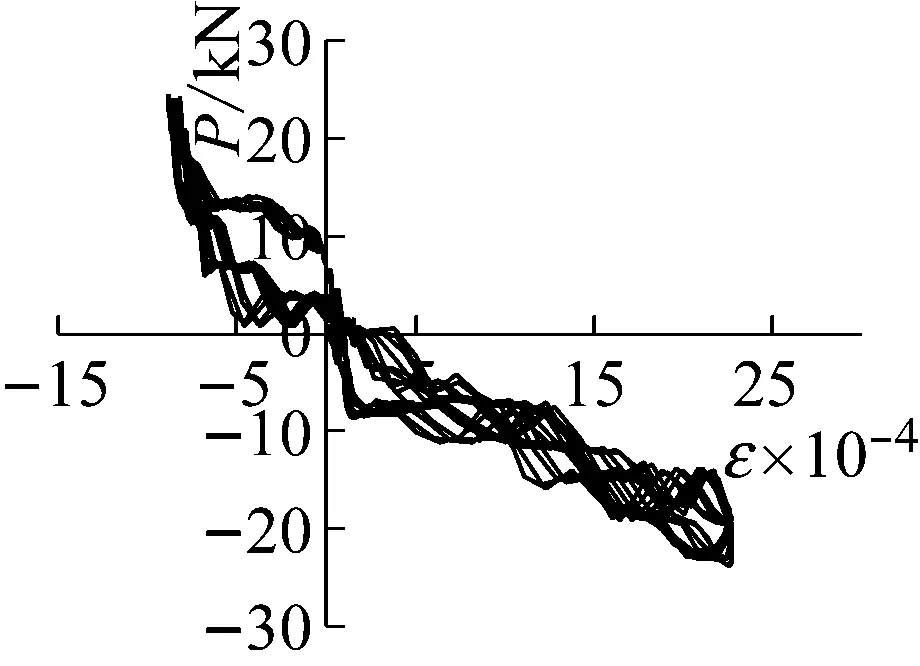
(b) SLJ-1测点2工况14

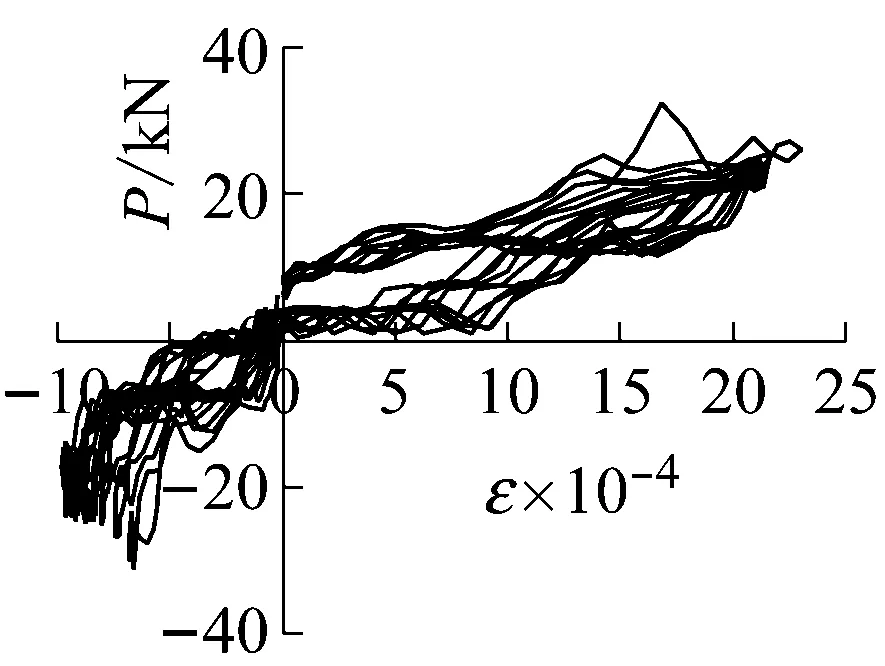
(c) SLJ-1测点7工况11

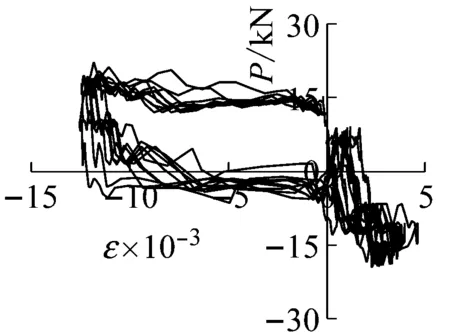
(d) SLJ-1测点7工况17

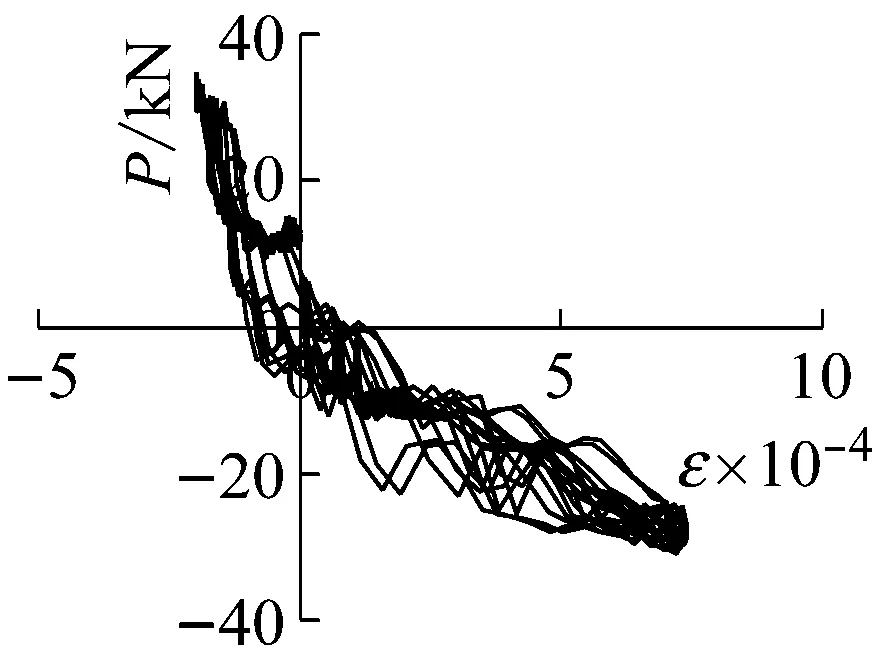
(e) SLJ-1测点1工况18

试件SLJ-1测点7的水平荷载-应变曲线如图7(c)、7(d)所示，在工况11时，该处最大应变值已达到2 400 με，超过了材料的屈服应变值，说明已进入弹塑性工作状态；至工况17时，枋端纵筋应变值已达到11 600 με，残余应变较大。

试件SLJ-1测点1的荷载-应变曲线如图7(e)示，加载至工况18时，箍筋最大应变值约为860 με，小于材料屈服应变值，且几乎无残余应变，说明核心区仍在弹性工作阶段，满足“强节点，弱构件”抗震设防要求，试件破坏位置在枋端塑性铰区域，结合试验过程中观察到的试件破坏现象，判断为梁铰破坏机制。

3.1.2 SLJ-2应变分析

试件SLJ-2测点2，其荷载-应变曲线如图8(a)、8(b)示，在工况10时最大应变值在480 με以内，明显小于材料的屈服应变值，且该值小于试件SLJ-1对应工况下同一位置应变值，试件卸载后几乎无残余应变，说明试件仍处于弹性工作阶段；随着加载的继续，至工况15时，该处钢筋应变值已达到2 600 με，明显超过材料屈服应变值，卸载后存在残余应变，说明试件进入到弹塑性工作阶段。

SLJ-2试件测点7，其荷载-应变曲线如图8(c)、8(d)示，在工况11时，该处最大应变值已达到了10 000 με，表明该工况下，该处已进入到弹塑性工作状态；至工况17时，枋端纵筋应变值已达到12 600 με，残余应变较大，说明在屈服前，黏滞阻尼器可减小试件的应变，屈服后对应变变化无明显影响。

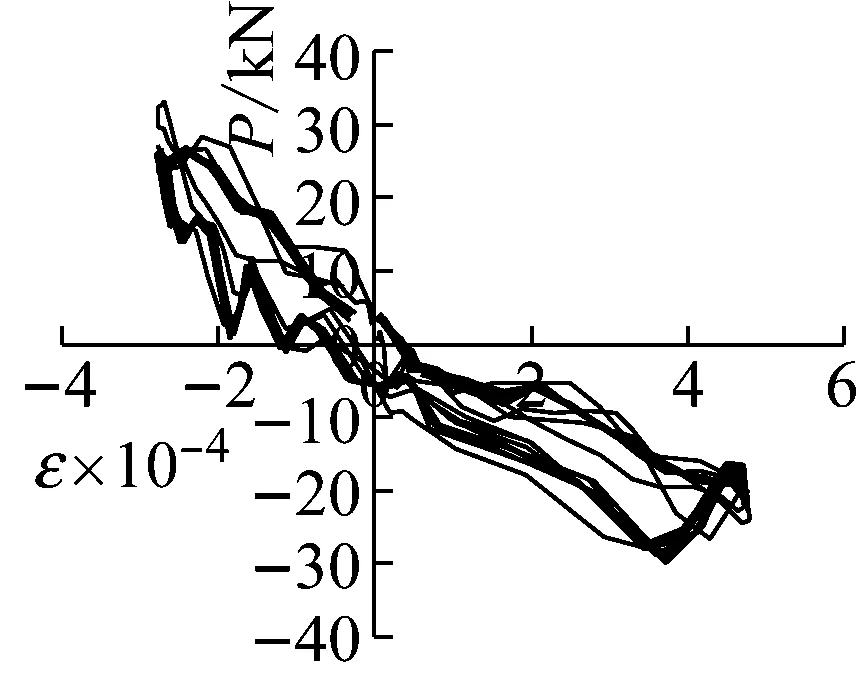
(a) SLJ-2测点2工况10

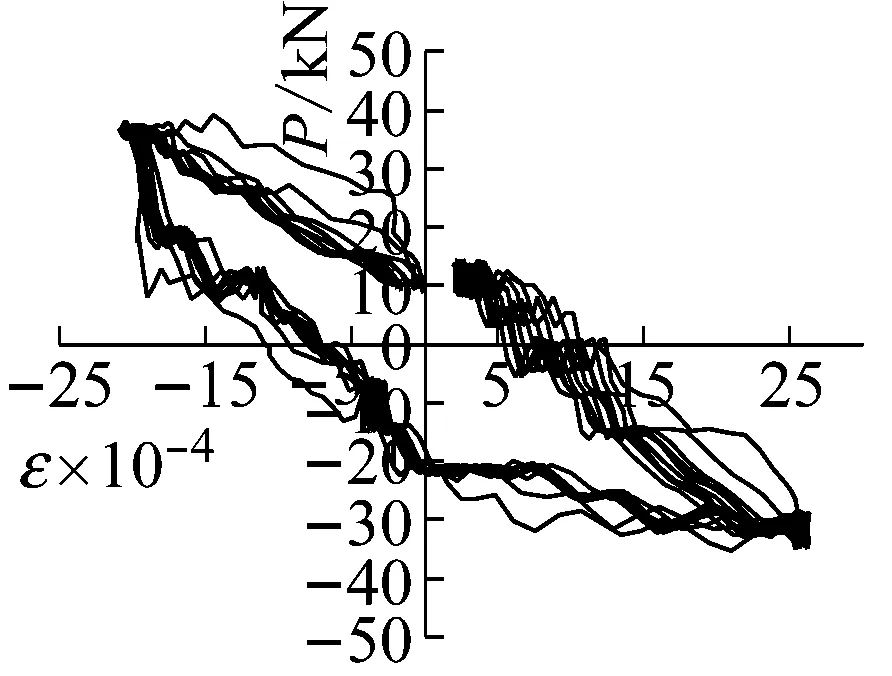
(b) SLJ-2测点2工况15

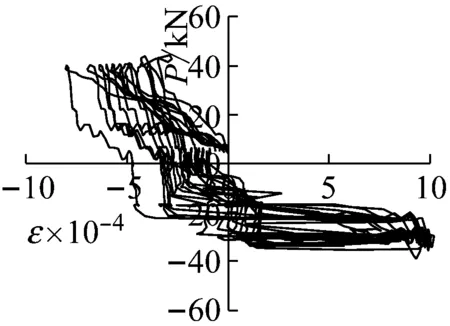
(c) SLJ-2测点7工况11

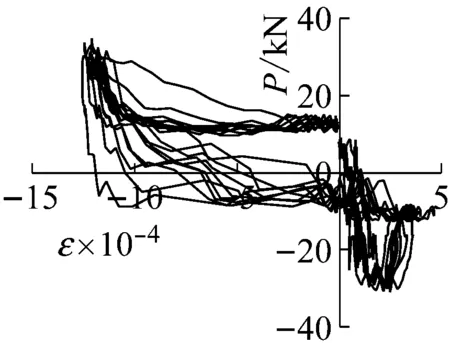
(d) SLJ-2测点7工况17

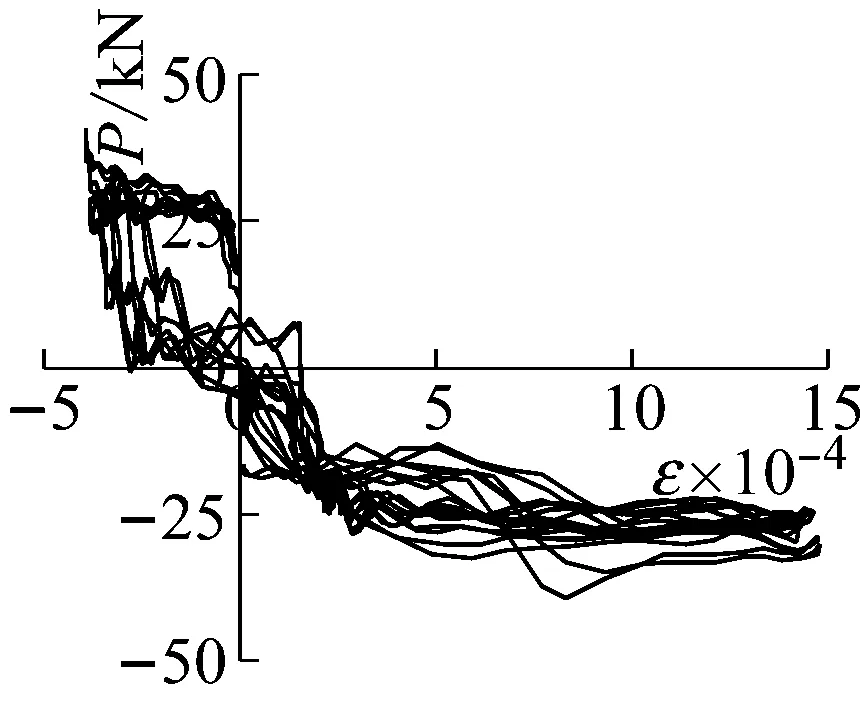
(e) SLJ-2测点1工况19

位于柱核心区位置的SLJ-2试件测点1，其荷载-应变曲线如图8(e)示，加载至工况19时，该处箍筋最大应变值约为1 500 με，略大于材料屈服应变值，几乎无残余应变，说明核心区由弹性工作阶段向弹塑性阶段工作阶段过渡，满足“强柱弱梁、强剪弱弯、强节点，弱构件”抗震设防要求试件破坏位置在枋端塑性铰区域，结合试验过程中观察到的试件破坏现象，最终判断为梁铰破坏机制。

3.2试件水平荷载-位移滞回曲线

滞回曲线主要由滞回环构成，综合反映了结构或构件的抗震性能，及构件的承载能力、延性性能、刚度退化规律和耗能能力等性能，是对结构或构件进行弹塑性分析的主要依据。试件P-Δ滞回曲线如图9所示，图中P为柱顶水平荷载，Δ为相应的柱顶水平位移。

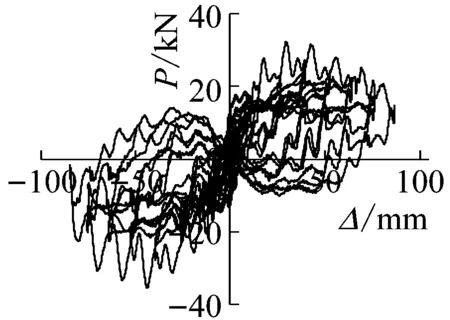
(a) SLJ-1荷载-位移滞回曲线

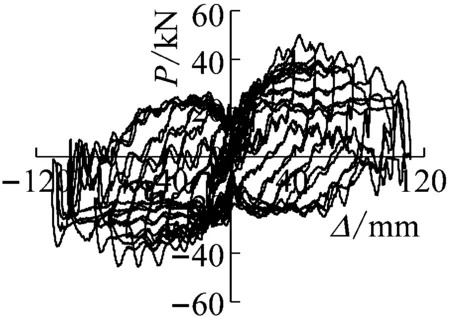
(b) SLJ-2荷载-位移滞回曲线

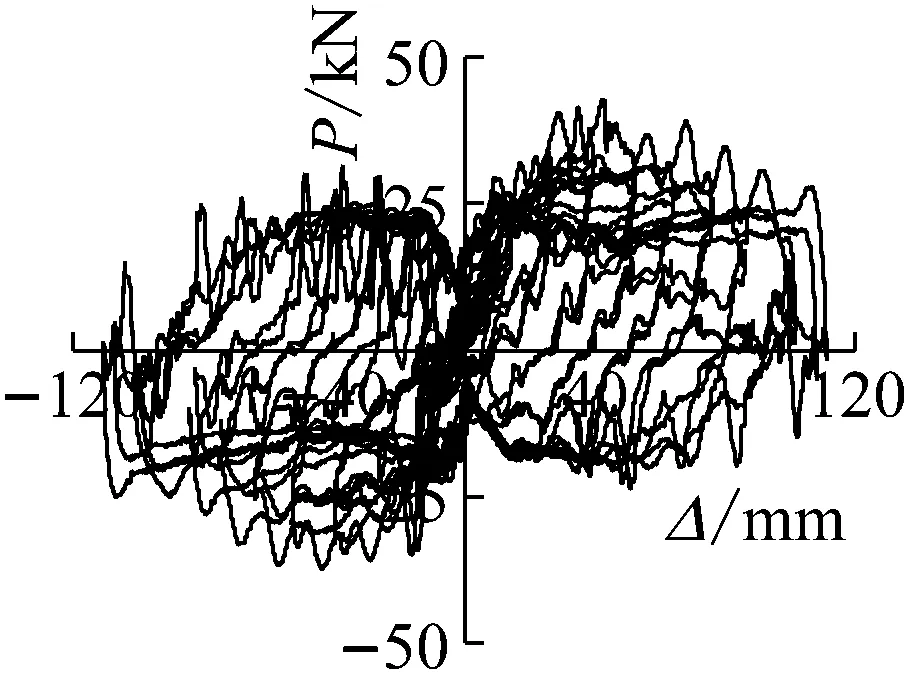
(c) SLJ-3荷载-位移滞回曲线

由图9可知，仿古建筑混凝土枋-柱节点滞回曲线具有以下主要特点：

(1) 总体上，滞回曲线饱满，表现出良好的耗能能力；

(2) 当荷载较小时，水平荷载-位移滞回曲线包络面积较小，荷载与位移基本呈直线关系，表明试件处于弹性工作阶段，刚度退化不明显，卸载至零，几乎无残余变形，试件耗能能力小；

(3) 随着荷载增大，滞回环包络面积逐渐增大，滞回曲线逐渐向位移轴倾斜，试件刚度逐渐退化，这是由于随着荷载的增大，枋端钢筋屈服及混凝土压碎的范围也逐渐增大，试件由弹性工作阶段逐步过渡到弹塑性阶段导致；

(4) 附设黏滞阻尼器的试件进入弹塑性工作阶段后，水平荷载-位移曲线会经历较长的接近水平的强化阶段，且其承载力明显高于未布置黏滞阻尼器的无控结构，表明黏滞阻尼器的附设可显著提高试件的承载力；

(5) 附设黏滞阻尼器的试件滞回曲线较无控结构更加饱满，包络的面积更大，说明附设黏滞阻尼器后的节点试件具有更优的耗能能力和抗震性能；

3.3黏滞阻尼器阻尼力-位移滞回曲线

以试件SLJ-2黏滞阻尼器阻尼力-位移曲线为例，选取工况10、工况19、工况23等典型工况下黏滞阻尼器阻尼力-位移曲线分析,如图10所示。

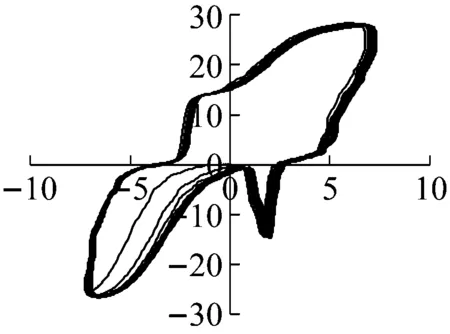
(a) 工况10时西侧

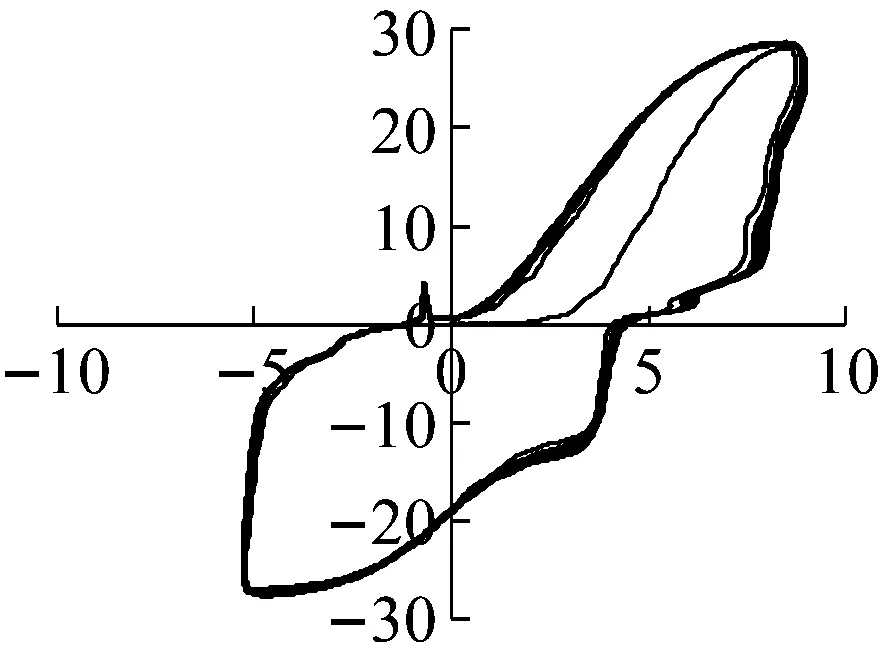
(b) 工况10时东侧

(c) 工况19时西侧

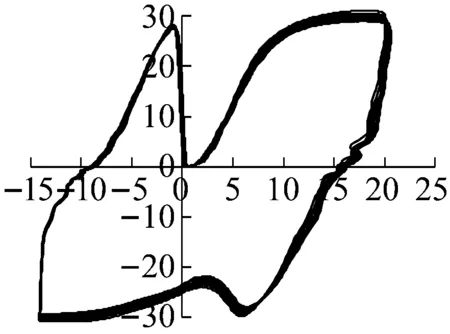
(d) 工况19时东侧

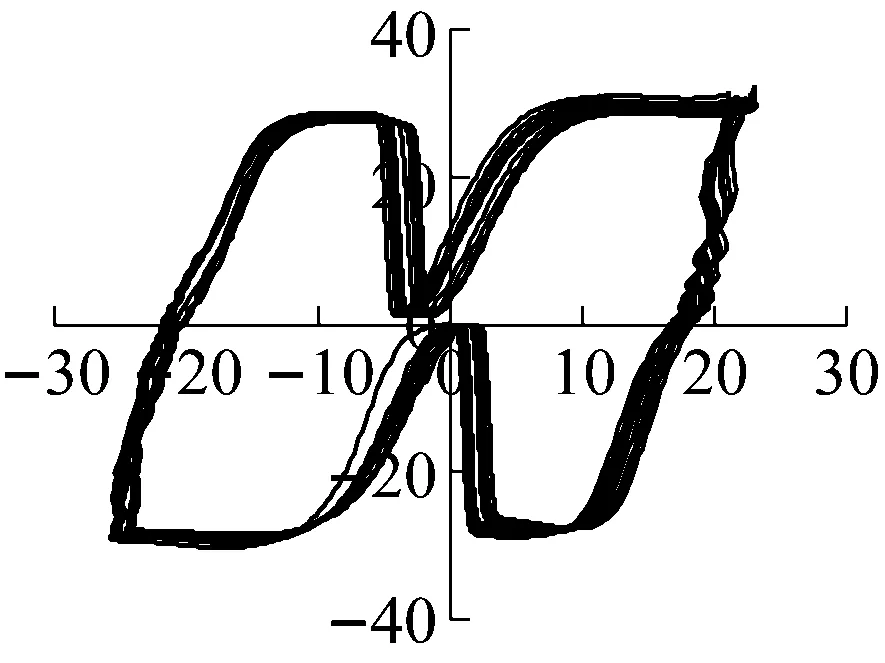
(e) 工况23西侧

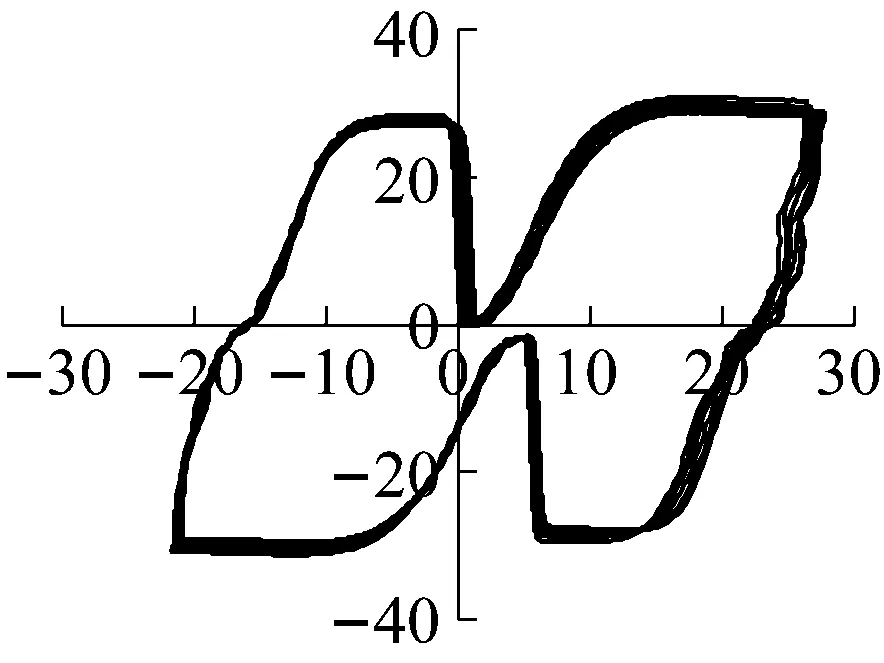
(f) 工况23东侧

由图10可知：

(1) 随着控制位移的不断增大，黏滞阻尼器的阻尼力及轴向位移不断增大，说明输入的能量越大，则黏滞阻尼器的反应越大，更利于确保结构的正常使用；阻尼器阻尼力-位移曲线最大荷载随着加载速率的不同而不同，反应了黏滞阻尼器作为速度相关型阻尼器的特征。

(2) 黏滞阻尼器的阻尼力-位移曲线较为饱满，说明该阻尼器具有较好的耗能能力。黏滞阻尼器的阻尼力-位移滞回曲线具有一定的倾角，这是由于黏滞阻尼器虽然本身不具有刚度，但在加载的瞬间，黏滞阻尼器具有一定的“瞬时刚度”，同时，曲线的斜率表示黏滞阻尼器的储能刚度，并且曲线的斜率并不是固定的，而是随着荷载的不断增大而发生变化，黏滞阻尼器的弹性刚度为一种动态刚度。

(3) 从黏滞阻尼器阻尼力-位移曲线上看出，滞回曲线并不完全重合，具有一定的“错动”，且该“错动”随着工况控制位移的增大而愈加明显，这是由于在加载过程中试件存在损伤累积，从而使得试件刚度及强度退化导致的。

(4) 黏滞阻尼器的阻尼力-位移滞回曲线在位移零点附近存在“凹陷”现象，这是由于试验加载制度造成的，试验过程中，同级位移加载以循环后会稍微停顿一下，然后在进行下一循环的加载，因此，每一循环加载起始时阻尼器活塞都从中间位置起步，并在中间位置结束，此时，活塞的运动速度下降至零，因此阻尼器的阻尼力也下降至零，导致阻尼器的滞回曲线在零点附近存在“凹陷”现象。

(5) 黏滞阻尼器阻尼力-位移滞回曲线沿位移轴有一定的平移错动，这是由于黏滞阻尼器在安装的过程中存在一定的空隙，且黏滞阻尼器在注油的过程中可能存在气泡。

3.4试件水平荷载-位移骨架曲线

采用“Park法”[12]确定试件的屈服点，相应坐标即为屈服荷载Py和屈服位移Δy。破坏荷载Pu定义为0.85Pm，相应的柱顶水平位移定义为破坏位移Δu。Pm为柱顶极限荷载，相应的柱顶位移为Δm。各试件的骨架曲线如图11所示，各特征点处相应的荷载及位移列于表4中。

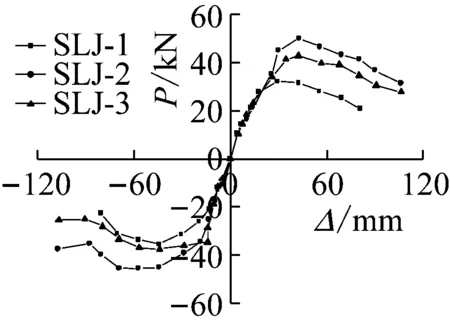
图11 试件骨架曲线

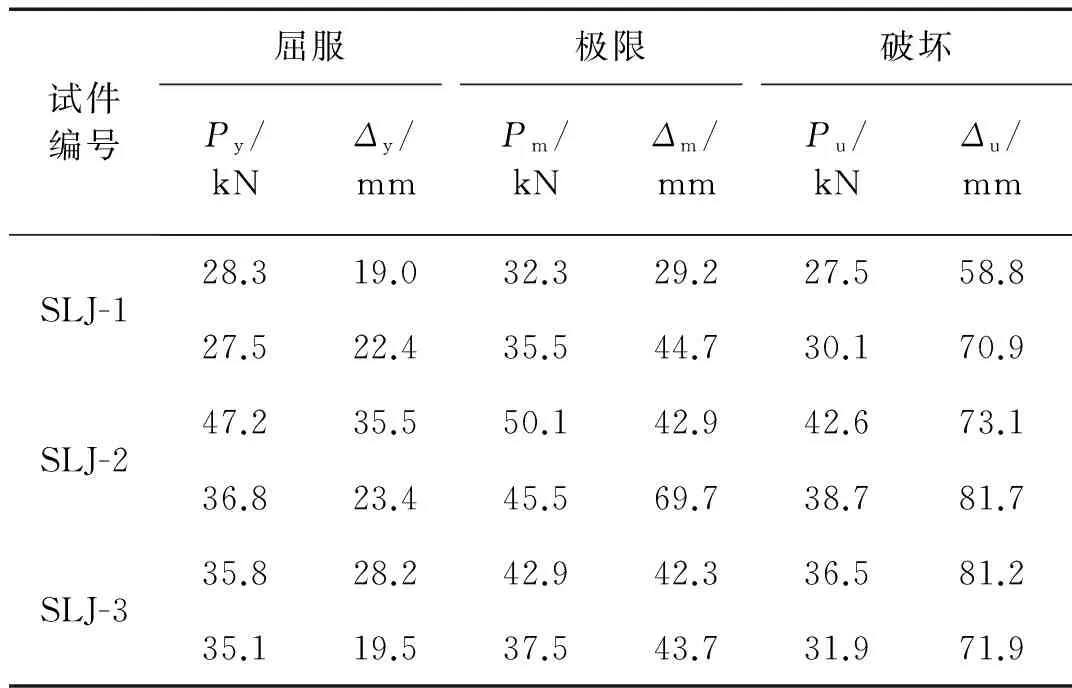
试件编号屈服极限破坏Py/kNΔy/mmPm/kNΔm/mmPu/kNΔu/mmSLJ-128.319.032.329.227.558.827.522.435.544.730.170.9SLJ-247.235.550.142.942.673.136.823.445.569.738.781.7SLJ-335.828.242.942.336.581.235.119.537.543.731.971.9

由图11及表4可知：

(1) 试件在恒定竖向荷载和水平往复荷载作用下经历了开裂、屈服、极限和破坏四个阶段，但在试件骨架曲线上并未出现屈服拐点，说明试件的屈服是一个从局部向整体逐渐扩散的过程。根据试验测试结果，可将枋端钢筋开始屈服，试件滞回曲线出现拐点作为试件屈服标志。

(2) 通过与已有的试验结果[13]相比较，可知：与钢筋混凝土框架结构节点相比，未附设黏滞阻尼器的仿古建筑混凝土枋-柱节点延性及耗能能力要弱于普通混凝土梁-柱节点，但附设黏滞阻尼器的有控结构，耗能能力要优于普通混凝土梁-柱节点，其骨架曲线有平缓的下降段。

(3) 试件SLJ-2、SLJ-3抵御外荷载的能力明显高于对比试件SLJ-1，且破坏阶段时，其骨架曲线下降段相对于无控结构较平缓，说明附设黏滞阻尼器可显著提高试件抵御外荷载的能力及延性性能。

(4) 与试件SLJ-3相比，附设设计荷载较大的黏滞阻尼器的试件SLJ-2具有更高的极限荷载，且其骨架曲线与坐标轴所围成的面积相对较大，但其骨架曲线的下降段相对较陡，表明增大黏滞阻尼器的设计荷载能在一定程度上提高试件的承载力。

3.5延性及耗能能力分析

各试件位移延性系数及耗能能力指标如表5、表6所示。其中位移延性系数μ为试件达到破坏时的柱顶水平位移Δu与试件达到屈服荷载时柱顶水平位移Δy之比。结构耗能能力采用等效黏滞阻尼系数he及功比系数IW[14]表征。

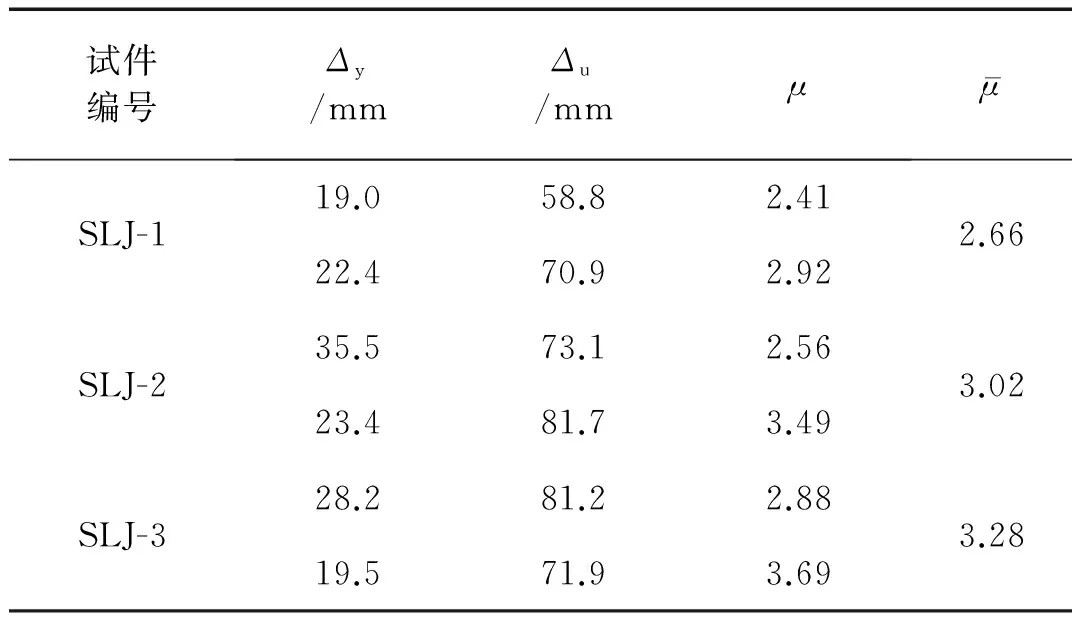
表5 试件延性系数

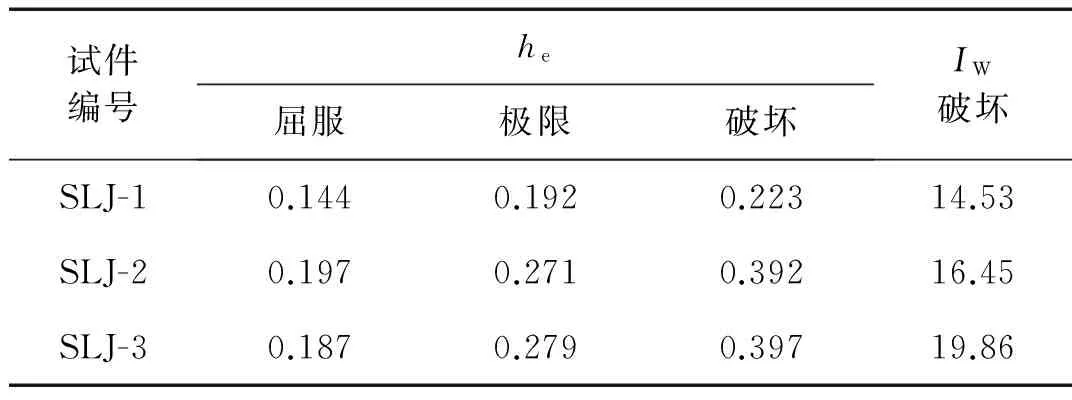
表6 试件耗能指标

由表5、表6可以看出：

(1) 试件SLJ-1位移延性系数要低于试件SLJ-2、SLJ-3，说明附设黏滞阻尼器可在一定程度上提高试件的延性。

(2) 试件SLJ-2位移延性系数要明显高于试件SLJ-3，说明不同型号的黏滞阻尼器对提高仿古建筑混凝土枋-柱节点的延性程度不同，对于本类型试件，附设黏滞阻尼器设计荷载大的试件位移延性更优良。

(3) 试件SLJ-2、SLJ-3的等效黏滞阻尼系数明显高于试件SLJ-1，屈服荷载时，he提高约为23.0%～26.9%；极限荷载时，he提高约为29.2%～31.2%；破坏荷载时，he提高约为43.1%～43.8%，说明附设黏滞阻尼器可显著提高试件的耗能能力。

(4) 试件SLJ-2所布置的黏滞阻尼器设计荷载要大于试件SLJ-3，但其极限荷载及破坏荷载时的he要低于试件SLJ-3，说明所布置的黏滞阻尼器设计荷载大小与试件耗能能力并没有正比关系，并非是黏滞阻尼器设计荷载大的试件耗能能力大。

(5) 通过与已有的研究结果[13]相比较，极限荷载时，普通钢筋混凝土节点等效黏滞阻尼系数为0.1左右，型钢混凝土节点的等效黏滞阻尼系数约为0.3，而本试验试件he为0.192～0.279，说明该类型节点耗能能力强，耗能指标满足结构抗震设计的要求。

(6) 试件功比系数均较大，说明结构在超过了其极限点之后的下降阶段仍具有较高的耗能能力。试件SLJ-2、SLJ-3的功比系数均大于SLJ-1，且根据已有研究结果[15-16]，钢筋混凝土结构、钢结构在破坏点的功比系数分别约为10、40，表明附设黏滞阻尼器后试件具有优于普通混凝土构件的耗能能力，布置黏滞阻尼器可大幅度提升试件的整体抗震性能及力学性能。

3.6刚度退化分析

结构或构件在同一级位移下控制点不同循环周次之间的刚度退化可用割线刚度Ki表示。割线刚度按式(2)计算。其含义是试件第i次加载循环的割线刚度等于第i次循环的正负最大荷载的绝对值之和与相应变形绝对值之和的比值。割线刚度按下式计算：

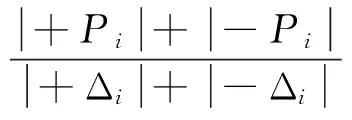
(2)

式中：+Pi(-Pi)为正(负)向加载时第i次加载循环峰值荷载；+Δi(-Δi)为正(负)向加载时第i次加载循环峰值荷载对应的位移值。

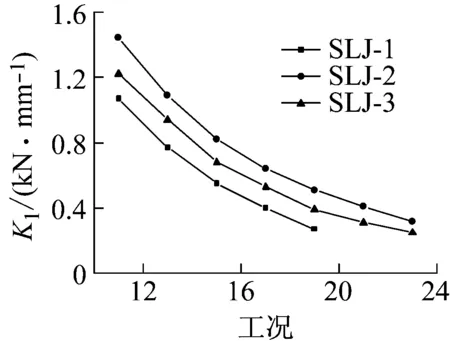
图12 刚度退化曲线

由于试件在弹性阶段没有明显的刚度退化现象，故取试件从弹塑性阶段到破坏阶段的刚度作为研究对象。试件刚度退化曲线如图11所示，从图中可知：

(1) 各试件的割线刚度随着加载位移的增大而降低，反映了试件在水平反复荷载作用下的刚度退化；究其原因随着荷载的增大，试件累积损伤增大，混凝土开裂剥落，钢筋屈服等。

(2) 各试件的刚度退化曲线基本平行，说明各试件刚度退化规律基本一致，在试件屈服后刚度下降速率逐渐变得平缓，最后趋于稳定。

(3) 试件SLJ-2、SLJ-3刚度退化规律虽大致相同，但SLJ-3试件在刚度开始退化时要明显小于SLJ-2试件，说明黏滞阻尼器荷载设计值对试件刚度退化并没有直接关系。

4 结 论

通过3个仿古建筑混凝土枋-柱节点的动力试验，包括2个附设黏滞阻尼器的试件及1个未附设黏滞阻尼器的对比试件，得到节点受力特点和抗震性能的主要结论如下：

(1) 试验中试件的破坏机制虽都为梁铰破坏机制，但破坏过程受试件是否附设黏滞阻尼器影响较大，对于无控结构，试件因形成梁铰机制，变成可变体系，不适宜继续加载，终止试验；对于有控结构，试件虽形成梁铰机制，但黏滞阻尼器可作为支撑存在，防止结构变成可变体系。

(2) 附设黏滞阻尼器可显著提高试件抵御外荷载的能力及耗能能力，在一定程度上可提高试件的延性性能。

(3) 附设黏滞阻尼器的试件破坏时，等效黏滞阻尼系数he=0.392～0.397，功比系数IW=16.4～19.8，其耗能能力优于普通混凝土梁-柱节点耗能能力。

(4) 达到屈服荷载后，刚度下降速率逐渐变的平缓，最后趋于稳定；对于有控试件，试件刚度退化与所附设黏滞阻尼器设计荷载并无直接关系。

[1] 薛建阳,吴占景,隋龑,等. 传统风格建筑钢结构双梁-柱中节点抗震性能试验研究及有限元分析[J].工程力学,2016,33(5):97-105.

XUE Jianyang,WU Zhanjing, SUI Yan,et al. Experimental study and numerical analysis on seismic performance of steel double beams-column interior-joints in traditional style building[J]. Engineering Mechanics,2016, 33(5):97-105.

[2] 高延安,杨庆山,王娟,等. 环境激励下古建筑飞云楼动力性能分析[J]. 振动与冲击,2015,34(22):144-148.

GAO Yanan,YANG Qingshan,WANG Juan, et al. Dynamic performance of the ancient architecture of Feiyun pavilion under the condition of environmental excitation[J].Journal of Vibration and Shock,2015,34(22):144-148.

[3] 李朋.传统风格建筑钢筋混凝土梁-柱节点抗震性能研究[D].西安:西安建筑科技大学,2014.

[4] MARKRIS N, CONSTANTINOU M C. Viscous dampers: testing, modeling, application in vibration and seismic isolation[C]// National Center for Earthquake Engineering Research. Technical Report NCEER-90-028n[R].Buffalo, New York:1990.

[5] 欧进萍, 吴斌, 龙旭, 等. 北京饭店消能减震抗震加固分析与设计:时程分析法[J].地震工程与工程振动,2001,21(4):82-87.

OU Jinping, WU Bin, LONG Xu, et al. Analysis and design of seismic retrofit of Beijing Hotel with energy dissipation: Time history method[J].Earthquake Engineering and EngineeringVibration,2001,21(4):82-87.

[6] 梁思成.清.工程做法则例图解[M].北京:清华大学出版社,2006.

[7] HOUSNER G W, BERGMAN L A, CAUGHEY T K, et al. Structural control: past, present, and future[J]. Journal of Engineering Mechanics, 1997, 123(9): 897-971.

[8] 建筑抗震设计规范:GB50011—2010[S].北京:中国建筑工业出版社, 2010.

[9] 中国地震烈度表:GB/T 17742—2008[S].北京:中国建筑工业出版社,2008.

[10] Highway Innovative Technology Evaluation Center. Guidelines for the testing of seismic isolation and energy dissipation devices[R].Technical Evaluation Report No: 40404.

[11] 建筑消能阻尼器:JGT209—2012[S].北京:中国标准出版社.2012.

[12] ELNASHAI A S, BRODERICK B M, DOWLING P J. Earthquake-resistant composite steel/concrete structures[J]. Structural Engineer, 1995, 73: 121-121.

[13] 韩林海.钢管混凝土结构: 结构与实践[M]. 北京:科学出版社,2007.

[14] GOSAIN N K, JIRSA J O, BROWN R H. Shear requirements for load reversals on RC members[J]. Journal of the Structural Division, 1977, 103(7): 1461-1476.

[15] WANG C, FOLIENTE G C, SIVASELVAN M V, et al. Hysteretic models for deteriorating inelastic structures[J]. Journal of Engineering Mechanics, 2001, 127(11): 1200-1202.

[16] SONG J K, PINCHEIRA J A. Spectral displacement demands of stiffness and strength degrading systems[J]. Earthquake Spectra, 2000, 16(4): 817-851.

Testsfordynamicperformanceofaconcretelintel-columnjointwithaviscousdamperinarchaizedbuildings

XUE Jianyang, DONG Jinshuang, SUI Yan, QI Liangjie, XU Dan

(College of Civil Engineering, Xi’an University of Architecture & Technology, Xi’an 710055, China)

In order to analyze aseismic behaviors of a concrete lintel-column joint with a viscous damper in archaized buildings under seismic actions, 3 specimens were made including two ones with viscous dampers called controlled structures and one without viscous damper called non-controlled structure. The dynamic tests were conducted for these 3 joints. Their failure process and patterns were observed. Their failure characteristics, load-displacement hysteretic curves, skeleton curves, load-bearing capacity and stiffness degradation were analyzed. The test results indicated that the load-bearing capacity of two controlled structures is obviously higher than that of the non-controlled structure, the mean values of their yield load increase value and ultimate load increase value are 27.4% and 22.4%, respectively; meanwhile, the displacement ductility and the energy-dissipating ability of two controlled structures are superior to those of the non-controlled one. Compared with the non-controlled structure, the equivalent viscous damping coefficient of two controlled structures is improved by 27.3%～30.8%; so, the aseismic performance of the controlled structures is superior to that of the non-controlled one.

archaized building; concrete; dynamic test; aseismic behavior; viscous damper

国家自然科学基金(51208411)；陕西省科学技术研究发展计划(2013KW23-01)

2016-04-26 修改稿收到日期：2016-07-16

薛建阳 男，博士，教授，1970年生

TU375

： A

10.13465/j.cnki.jvs.2017.17.032