半球壳冲击土壤的SPH-FEM耦合分析方法

罗 杰， 肖建春， 马克俭， 毛家意

(1.贵州大学 空间结构研究中心，贵阳 550003； 2.贵阳市人民防空办公室，贵阳 550003)

半球壳冲击土壤的SPH-FEM耦合分析方法

罗 杰1， 肖建春1， 马克俭1， 毛家意2

(1.贵州大学 空间结构研究中心，贵阳 550003； 2.贵阳市人民防空办公室，贵阳 550003)

SPH方法作为一种具有无网格、拉格朗日性质的动力学求解算法，已经广泛应用于冲击动力学的研究。采用SPH-FEM耦合分析和8组试验进行半球壳冲击土壤的对比分析，比较加速度时程曲线和局部变形图，验证SPH-FEM方法在处理此类问题中的适用性。利用SPH-FEM方法得到的能量和冲击力时程曲线，归纳出土壤的能量耗散机理。分析表明，数值模拟结果和试验结果吻合较好，SPH-FEM方法能胜任模拟半球壳冲击土壤的整个过程。土壤是一种很好的能量缓冲体。

SPH-FEM；冲击；土壤；半球壳；加速度

土壤是由大量离散固体颗粒组成的集合体，是一种复杂的非平衡态的能量耗散体系。当受到冲击时，部分颗粒会呈现流体的现象，并会发生强烈挤压和摩擦[1]。散体的这些性质，很难找到一种具体模型来描述。目前散体的动力学行为还没有成熟的理论，因此研究人员一般采用数值模拟和实验来进行分析[2-3]。由于试验复杂且影响因素过多，数值模拟方法是研究土壤受冲击的重要手段之一。近年来，适合于大变形分析的离散介质力学方法和无网格方法等逐渐发展起来。其中离散介质力学方法可以真实地表达求解区域中的几何状态以及大量的不连续面，易于处理大变形、大位移和和动态问题；而无网格法则将整个求解区域离散为独立的节点，对网格没有依赖性，并基于大变形理论建立了不同无网格理论框架下可进行大变形问题分析的计算方法[4]。然而，它们的适用性亦存在一定的缺陷，原因在于，这些方法中非物理参数不易确定，难以直接描述土体的应力-应变关系，限制了其在本研究方向上的应用[5-6]。

光滑粒子流体动力学(SPH)是一种无空间网格的连续介质动力学计算方法。这种方法最初主要用于研究天体物理现象[7-9]，目前该方法的研究成果已涉及多个领域[10-15]。近年来，SPH方法开始涉及土体材料特性的研究，已被应用在山体滑坡，挖孔成桩等土体大变形问题中[16]。这些研究均证明SPH方法能够精确描述土体在不同不变形阶段的力学性质，并具有较高的计算精度和稳定性[17]。与有限元或离散元等数值方法相比，SPH由于其拉格朗日和自适应特性，可以很好地处理大变形和后失稳问题，避免了有限元计算中的网格过度扭曲可能导致的计算失败，或离散单元法计算工作量大和参数标定困难等问题，因此是量化及解释土体大变形和后失稳机理的有力工具。本文采用SPH-FEM方法模拟土壤受冲击的整个过程，通过与试验数据对比，并对数值结果进行了详细的验证分析，证明该方法在处理土壤受冲击问题中的适用性。该研究为以后分析散体介质受冲击的动力学行为提供了一种稳定的数值模拟方法，为以后的研究工作奠定了基础。

1 理论基础

2.1SPH基础[18]

连续体偏微分方程的求解可转化为粒子的运动方程而求解, 而每个粒子的场变量通过积分插值获得：

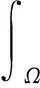
(1)

在SPH方法中，整个系统是由具有独立的质量，占有独立空间的有限个粒子表示的。SPH计算时, 通过对支持域内的离散粒子求和来代替式(1)中的连续积分:

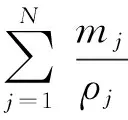
(2)

SPH方法通过使用光滑函数引进积分表示式。光滑函数不仅决定了函数近似式的形式、定义粒子支持区域的尺寸，而且还决定核近似的一致性和精度。本文采用的光滑核函数是B样条曲线：

(3)

流体动力学的基本控制方程是基于质量守恒，动量守恒，能量守恒三条基本的物理守恒定律来得到的。

1.2SPH-FEM算法流程

在交界面上SPH粒子与FE单元耦合，通过罚函数将质点的力转换到FE单元表面。当SPH粒子与FE单元接触时，更新SPH粒子与FE单元节点的位移与速度等变量，产生接触力。流程见图1。

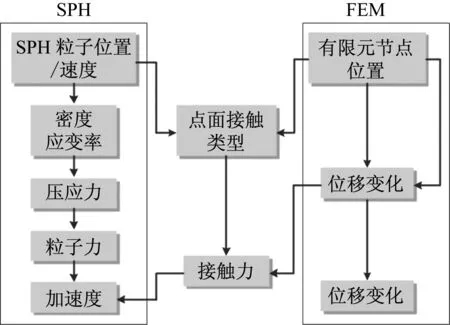
图1 SPH-FEM耦合算法流程

1.3时间步

SPH采用跳蛙格式求解Navier-Stokes方程，FEM采用中心差分格式求解显式动力学方程。在Lagrangian框架下要求SPH与FEM的耦合面上积分同步，在同一时间点进行数据传输[19]。FEM与SPH采用相同时间步。

ΔtSPH-FEM=min{ΔtSPH,ΔtFEM}

(4)

(5)

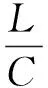
(6)

式中：h为SPH的光滑长度；L为最小单元尺寸；C为材料声速；α为时间步长比例系数。

2 冲击试验

图2为北京大学所做的撞击试验，一个半球壳以一定的初速度竖直撞击地面。通过不同高度释放具有不同直径和质量的半球壳，利用安装在半球壳中的加速度测量装置测得了球壳落在土壤中的加速度曲线[20]。根据不同的半球壳直径，质量以及撞击速度，实验共有8组，如表1所示。

图2 半球壳撞击试验

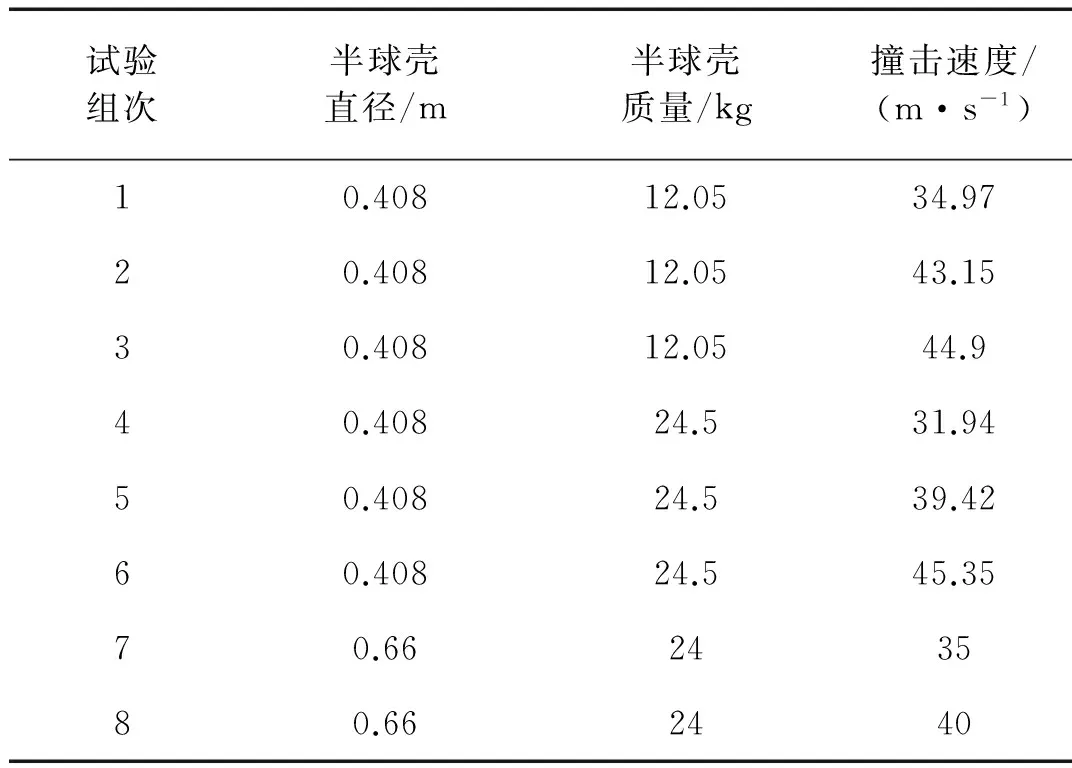
试验组次半球壳直径/m半球壳质量/kg撞击速度/(m·s-1)10.40812.0534.9720.40812.0543.1530.40812.0544.940.40824.531.9450.40824.539.4260.40824.545.3570.66243580.662440

在低速碰撞情况下，土壤颗粒很少跳起，但是球壳的冲击在土壤中形成沙坑。沙坑的外围出现空腔，同时球壳周围一圈的土壤将翻起而略高于土壤表面，如图1所示。

3 数值模型

3.1几何和网格模型

采用LS-Dyna对半球壳撞击试验进行SPH-FEM耦合方法数值分析，如图3所示。半球壳，四周及底面土壤采用有限元单元，内部土壤采用SPH粒子。土壤数值模型尺寸按经验确定：冲击后模型外侧最大应变小于0.001%，属于非常小应变[21]。通过模型调试，土壤数值模型尺寸1.1 m×1.1 m×0.55 m。大变形部分采用SPH模拟，SPH尺寸0.7 m×0.7 m×0.35 m。有限元单元为实体单元，按六面体单元划分网格，划分网格后半球壳共有8 908个单元，四周及底面土壤共有31 616个单元，内部土壤共有171 500个SPH粒子。

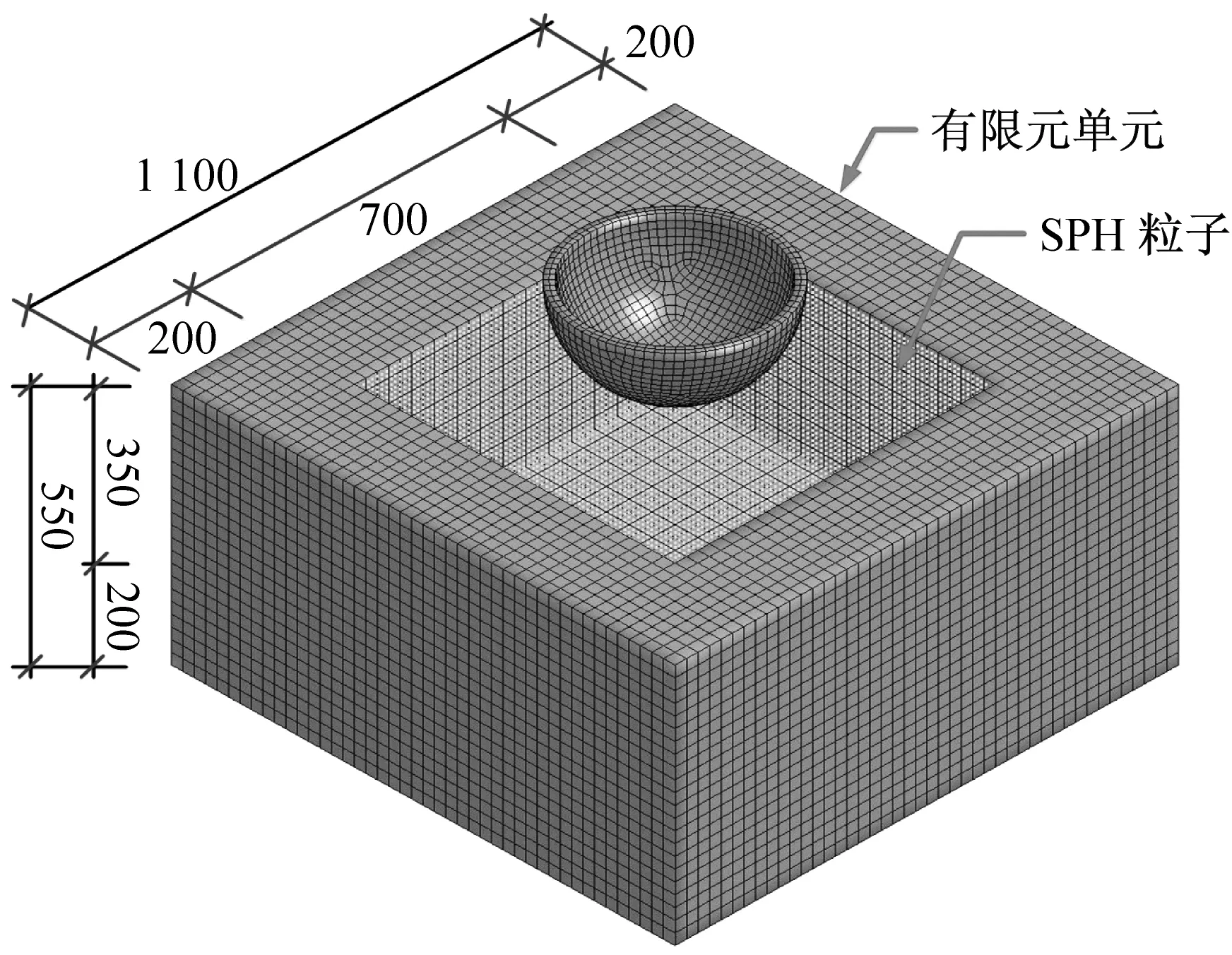
图3 半球壳撞击有限元模型

3.2材料模型

半球壳采用刚体模型，采用LS-Dyna提供的MAT147材料模型来作为土壤模型。此土壤材料采用修正的Mohr_Cloulomb 屈服准则，是一种适合于实体单元、考虑损伤的各向同性材料模型，其屈服面表达式[22]为

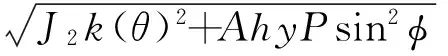
(7)

式中：P为压力；φ为内摩擦角；J2为应力张量的第二不变量；k(θ)为张量平面角函数；C为黏聚力；Ahyp为修正的Mohr_Cloulomb屈服面和标准的Mohr_Cloulomb屈服面相似程度。结合实验，土壤模型的主要材料参数见表2。

3.3模型边界

半球壳与土壤SPH粒子定义为侵蚀接触，土壤有限元单元与土壤SPH粒子定义为点面接触，以保证不同算法间的协调一致性。在SPH与FEM耦合处理中，将SPH粒子定义为从节点，将与SPH粒子接触界面上的有限元单元表面定义为主面。为了完全消除应力波反射作用，在模型四周及底面有限单元面施加无反射边界，以描述半无限土体空间。

表2 土壤材料参数

3.4数值计算结果与试验对比

选取试验1和试验3中加速度传感器得到的半球壳质心的加速度时程曲线与数值模拟得到的半球壳质心的加速度时程曲线进行对比，如图4，5所示。选取试验与数值模拟中的最大加速度值进行对比，如表3所示。通过对比发现，数值模拟得到的最大加速度非常接近试验得到的最大加速度。数值模拟结果和试验结果吻合的比较好，SPH-FEM方法能较好的模拟半球壳冲击土壤的整个过程。

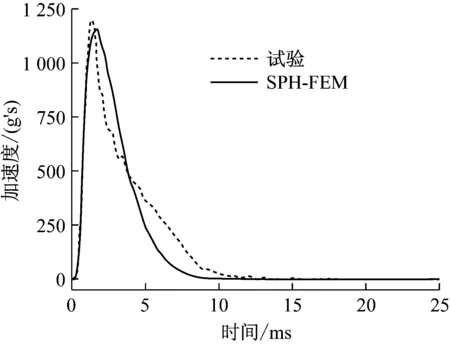
图4 试验1和SPH-FEM的加速度曲线对比

Fig.4 Comparison of acceleration curves of first experiment and SPH-FEM

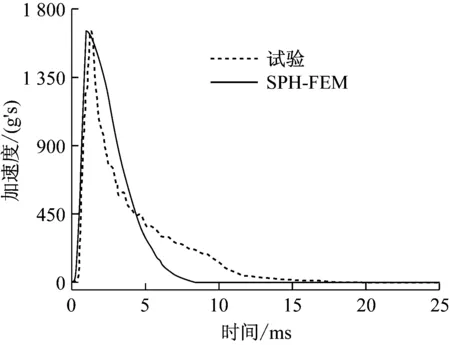
图5 试验3和SPH-FEM的加速度曲线对比

Fig.5 Comparison of acceleration curves of third experiment and SPH-FEM

表3 试验结果和SPH方法最大加速度对比(g=9.8 kg·m/s2)

数值模拟与试验有一定的误差，导致该误差的原因经分析主要在于以下几点原因：① 加速度传感器的响应频率偏小，对高频的测量不太准确(数值解在不同的时间步长下计算得到的加速度最大值相应的有所变化，时间步长越短得到的加速度值越大，数值解和试验结果的对比需要在加速度传感器的最高测量频率相比较)[20]；② 土壤的缓冲性能与土壤的密实度有密切关系。在一般无网格方法中土壤密实度通过密度来控制[20]，SPH方法均分粒子的质量大小来模拟土壤的密实度。该数值模型中的土壤模型密实度较大，起到的缓冲的作用较小，从而使得加速度下降过程比试验快(图3，4)。③ 该SPH算法中粒子与粒子之间忽略摩擦滑移。

半球壳初始位置位于土壤上方，与土壤无接触；开始瞬间与土壤接触，土壤由于受到剪切和挤压作用开始流动；随着与土壤接触面积的增大，土壤粒子流动范围逐渐变大。直到25 ms后观察土壤变化形状，如图6所示。土壤颗粒很少跳起，球壳的冲击在土壤中形成沙坑。球壳周围一圈的土壤将翻起而略高于土壤表面，这与试验现象描述相符。

图6 25 ms时半球壳冲击土壤的形状

Fig.6 Shape of the hemispherical shell impact the soil in 25 ms

3.5冲击能量分析

图7为第一组SPH-FEM数值模型的能量时程图。在冲击加载过程中，半球壳的初始动能部分转化为土壤的内能，部分土壤翻起、飞溅，以及单元失效删除耗散掉，还有一部分能量转化为接触能；半球壳与土壤接触后，土壤内能迅速上升，之后由于土壤单元损伤超过阀值，逐渐出现单元删除，土壤的内能逐渐下降，转化为土壤的侵蚀能。半球壳动能大部分被土壤吸收，转化为土壤内能，仅有很小一部分能量转化为侵蚀能、接触能和沙漏能。接触能、沙漏能为峰值内能的10%以内，是被认为可以接受的范围。另外SPH方法应用于动力学冲击时在冲击波波面应用质量守恒、动量守恒、能量守恒时要将动能转化为热能，提供冲击波波面的耗散，这种能量的转换往往需要采用人工黏度耗能的形式来表示，因此会产生一部分由人工黏度产生的能量。该耗量对于能量平衡是非常重要的，这使得该算法适合于模拟冲击波问题。图中人工黏度能量包含在砂土内能中。

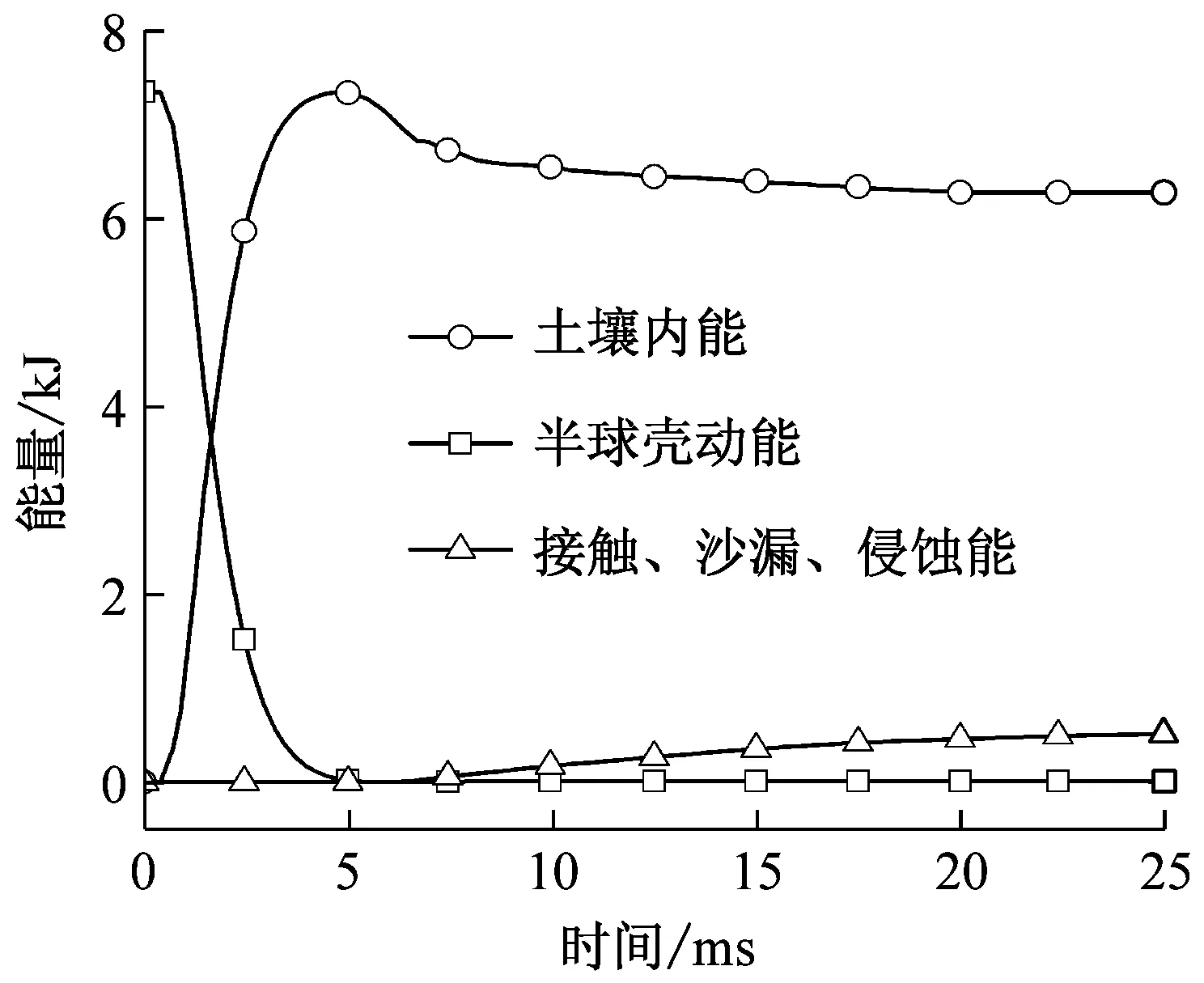
图7 第一组SPH-FEM数值模型能量时程图

3.6冲击力曲线

传统的SPH方法存在粒子压力场数值震荡问题，引入人工黏度参数来考虑粒子压力场影响。图8给出了半球壳与砂土之间的冲击力时程曲线。可见，在整个冲击作用过程中，冲击力时程曲线包括快速上升，快速下降，稳定三个阶段，即冲击力在极短的时间内增加，然后迅速减小到0。土壤是一种很好的缓冲材料，半球壳与颗粒及颗粒间产生激烈的碰撞，使冲击力得到衰减，从而达到了缓冲的效果。图中可以得出初始冲击能量越大，半球壳与土壤之间的冲击力越大。8组数值模拟冲击力变成0的时间均一样，都为10 ms。土壤是一种能量快速耗散体系且冲击力衰减时间与初始动能和半球壳直径无关。

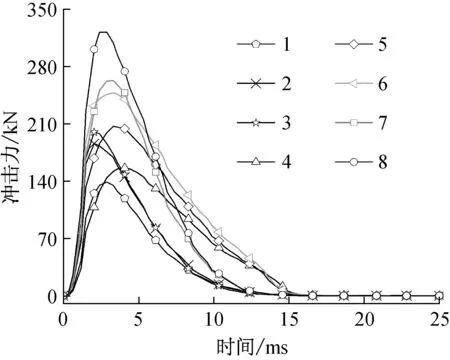
图8 8组数值模拟冲击力时程曲线

4 结 论

SPH-FEM耦合法能充分利用传统有限元法的高计算效率和光滑质点流体动力学法处理土体大变形的优势。正是由于这些优点，该方法已大量应用于岩土工程的研究中。本文通过采用SPH-FEM方法对土壤受冲击的过程进行分析，并与试验对比，得到以下结论：

(1) 利用SPH-FEM耦合算法得到的半球壳与土体碰撞时的局部变形行为以及加速度时程曲线与试验较为吻合，证明了这种算法是能够分析土壤受冲击的整个过程。

(2) 半球壳动能大部分被土壤吸收，转化为土壤内能，仅有很小一部分能量转化为侵蚀能、接触能和沙漏能。

(3) 通过数值模拟得到土壤是一种很好的缓冲材料；初始冲击能量越大，半球壳与土壤之间的最大冲击力越大。

[1] 庞勇，刘才山. 低速刚性体冲击密实散体介质的动力学实验与理论研究[C]// 中国力学大会暨钱学森诞辰100周年纪念大会. 哈尔滨市, 2011.

[2] GOLDMAN D I, UMBANHOWAR P. Scaling and dynamics of sphere and disk impact into granular media[J]. Physical Review E, 2008,77(1): 255-282.

[3] KATSURAGI H, DURIAN D J. Unified force law for granular impact cratering[J]. Nature Physics, 2007, 3(6): 420-423.

[4] 黄雨，郝亮，谢攀，等. 土体流动大变形的SPH数值模拟[J]. 岩土工程学报, 2009, 31(10): 1520-1524.

HUANG Yu, HAO Liang, XIE Pan, et al. Numerical simulation of large deformation of soil flow based on SPH method[J]. Chinese Journal of Geotechnical Engineering, 2009, 31(10): 1520-1524.

[5] SASAKI T, OHNISHI Y, YOHINAKA R. Discontinues deformation analysis and its application to rock mechanics problems[J]. Journal of Geotechnical Engineering, JSCE, 1994,Ⅲ-27: 11-20.

[6] BAXTER G W, BEHRINGER R P. Cellular automata models of granular flow[J]. Physical Review A, 1990, 42(2): 1017-1020.

[7] LUCY L B. A numerical approach to testing of the fission hypothesis[J]. The Astronomical Journal, 1977, 82: 1013-1024.

[8] GINGOLD R A, MONAGHAN J J. Smoothed particle hydrodynamics theory and application to non-spherical stars[J]. Monthly Notices of the Royal Astronomical Society, 1977, 181: 375-389.

[9] MONAGHAN J J, LATTANZIO J C. A refined particle method for astrophysical problem[J]. Astronomy and Astrophysics, 1985, 149(1): 135-143.

[10] MICHEL Y, CHEVALIER J M, DURIN C, et al. Hypervelocity impacts on thin brittle targets: experimental data and SPH simulations[J]. International Journal of Impact Engineering, 2006, 33: 441-451.

[11] CLEARY P W, SINNOTT M, MORRISON R. Prediction of slurry transport in SAG mills using SPH fluid flow in a dynamic DEM based porous media[J]. Minerals Engineering, 2006, 19(15): 1517-1527.

[12] FANG J N, OWENS R G, TACHER L, et al. A numerical study of the SPH method for simulating transient viscoelastic free surface flows[J]. Journal of Non-Newtonian Fluid Mechanics, 2006, 139(1/2): 68-84.

[13] 许庆新，沈荣瀛，周海亭. SPH方法在剪切式碰撞能量吸收器中的应用[J]. 振动与冲击, 2007, 26(9): 108-111.

XU Qingxin, SHEN Rongying, ZHOU Haiting. Applying SPH method to shearing energy absorbers[J]. Journal of Vibration and Shock, 2007, 26(9): 108-111.

[14] 沈燕鸣，何琨，陈坚强，等. SPH同一算法对自由流体冲击弹性结构体问题模拟[J]. 振动与冲击, 2015, 34(16): 60-65.

SHEN Yanming, HE Kun, CHEN Jianqiang, et al. Numerical simulation of free surface flow impacting elastic structure with SPH uniform method[J]. Journal of Vibration and Shock, 2015, 34(16): 60-65.

[15] 杨刚，傅奕轲，郑建民，等. 基于SPH 方法对不同药型罩线性聚能射流形成及后效侵彻过程的模拟[J]. 振动与冲击, 2016, 35(4): 56-61.

YANG Gang, FU Yike, ZHENG Jianmin, et al. Simulation of formation and subsequent penetration process of linear shaped charge jets with different liners based on SPH method[J]. Journal of Vibration and Shock, 2016, 35(4): 56-61.

[16] BUI H H, FUKAGAWA R, SAKO K, et al. Lagrangian mesh-free particle method (SPH) for large deformation and post-failure of geomaterial using elastic-plastic soil constitutive model[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2008, 32: 1537-1570.

[17] 黄雨，郝亮，野々山泶人. SPH方法在岩土工程中的研究应用进展[J]. 岩土工程学报, 2008, 30(2): 256-262.

HUANG Yu, HAO Liang, NONOYAMA Hideto. The state of the art of SPH method applied in geotechnical engineering[J]. Chinese Journal of Geotechnical Engineering, 2008, 30(2): 256-262.

[18] LIU G R, LIU M B. Smoothed particle hydrodynamics-a meshfree particle method[M]. New Jersey: World Scientific Publishing Company, 2003.

[19] 张志春，强洪夫，高巍然. 一种新型SPH-FEM耦合算法及其在冲击动力学问题中的应用[J]. 爆炸与冲击, 2011, 31(3): 243-249.

ZHANG Zhichun, QIANG Hongfu, GAO Weiran. A new coupled SPH-FEM algorithm and its application to impact dynamics[J]. Explosion and Shock Waves, 2011, 31(3): 243-249.

[20] 马炜. 散体介质冲击荷载作用下力学行为理论分析与算法实现[D]. 北京:北京大学, 2008.

[21] 汪中卫，王海飙，戚科骏，等. 土体小应变试验研究综述与评价[J]. 岩土力学, 2007, 28(7): 1518-1523.

WANG Zhongwei, WANG Haibiao, QI Kejun, et al. Summary and evaluation of experimental investigation on small strain of soil[J]. Rock and Soil Mechanics, 2007, 28(7): 1518-1523.

[22] LEWIS B A. Manual for LS-DYNA soil material model 147[R]. USA: Federal Highway Administration Research and Development Turner Fairbank Highway Research Center, 2004.

SPH-FEMcoupledmethodforanalyzingahemisphericalshellimpactsoil

LUO Jie1, XIAO Jianchun1, MA Kejian1, MAO Jiayi2

(1. Space Structure Research Center, Guizhou University, Guiyang 550003, China;2. Guiyang City People’s Air Defense Office, Guiyang 550003, China)

SPH method as a meshless Lagrange dynamic solving method is widely applied in studying impact dynamics. Here, the SPH-FEM coupled method and 8 tests were adopted to analyze a hemispherical shell impact soil. The acceleration time history curves and local deformations obtained with SPH-FEM coupled method were compared with those gained in tests to validate the applicability of SPH-FEM method. The energy dissipation mechanism of soil was generalized with the energy and impact force time history curves obtained using SPH-FEM method. The results showed that the numerical simulation results agree well with the test ones; SPH-FEM coupled method can be used to correctly simulate the whole process of a hemispherical shell impact soil, soil is a good energy buffer.

SPH-FEM; impact; soil; hemispherical shell; acceleration

国家自然科学基金(50978064)

2016-08-12 修改稿收到日期：2016-12-11

罗杰 男，博士生，1989年8月

肖建春，男，博士，教授，1967年9月

TD853

： A

10.13465/j.cnki.jvs.2017.17.029