考虑非线性阻尼的双稳态电磁式吸振器的动力学特性研究

刘丽兰， 任博林， 朱国栋， 杨倩倩

(西安理工大学 机械与精密仪器工程学院， 西安 710048)

考虑非线性阻尼的双稳态电磁式吸振器的动力学特性研究

刘丽兰， 任博林， 朱国栋， 杨倩倩

(西安理工大学 机械与精密仪器工程学院， 西安 710048)

将非线性阻尼引入到双稳态电磁式振动能量捕获器中，提出了考虑非线性阻尼的双稳态吸振器。建立了考虑非线性阻尼的双稳态吸振器和主系统的力学模型和数学模型。分析了考虑非线性阻尼的双稳态吸振器随非线性阻尼系数的分岔情况。数值仿真研究发现，特别是在频率共振区域，考虑附加非线性阻尼的双稳态吸振器比线性阻尼的双稳态吸振器对主系统减振更有优势。并进一步获得了主系统及考虑非线性阻尼的双稳态吸振器振动能量随非线性阻尼参数的变化曲线，发现了非线性阻尼对主系统减振及吸振器发电的影响规律。上述研究工作可为双稳态吸振器的研究提供参考。

非线性阻尼； 双稳态吸振器； 共振； 振动能量； 平均功率

随着精密加工技术的进步，采用有效的隔振或者吸振技术隔离来自基础的振动和设备自身的扰动日益重要。吸振或隔振技术一般分为主动隔振和被动隔振，主动隔振的吸振器在多频激励下具有较好的减振效果，但是要消耗能源，成本较高[1-2]。被动隔振是一种不需要外部能源的减震控制技术，一般是在结构的某个部位附加一个子系统，因其构造简单、造价低、易于维护且无需外部能源支持等优点而引起了广泛的关注。近年来一些学者发现，非线性吸振器具有振动抑制频带宽、附加质量小、可实现靶能量传递等诸多特点，将其应用到系统的减振和隔振中[3-6]。

通常系统的减振和隔振多采用线性弹簧、线性阻尼质量系统，也取得了较好的减振效果[7-9]。随着非线性动力学理论研究的深入，有研究表明振动控制系统采用非线性阻尼对减振更加明显，如Milovanovic等[10]分别研究了一个单自由度隔振系统附加线性黏性阻尼及立方刚度和附加立方阻尼及线性刚度的减振性能，通过分析系统的位移及相对位移响应，发现在共振区域时立方阻尼系统比线性黏性阻尼减振明显。文献[11-12]介绍了附加立方非线性阻尼的单自由度隔振系统，并理论证明了立方非线性阻尼在共振频率区域可以减少力的传递率，同时保证在其他频率区域内几乎不受影响。但是这些研究都只局限于单个自由度系统。Jing[13]研究了主系统附加线性刚度和非线性阻尼的吸振器，发现了吸振器在主系统振动控制方面有很多优点。另外，将吸振器吸收的能量转化为电能成为了新的研究热点[14-15]。

本文将非线性阻尼引入到双稳态电磁式振动能量捕获器中，在对主系统减振的同时，将吸收的振动能转化为有用的电能，提出了考虑非线性阻尼的双稳态电磁式振动吸振器，并建立了主系统附加非线性阻尼的双稳态吸振器的力学模型和数学模型。借助数值仿真分析，研究了频率共振区考虑非线性阻尼的双稳态吸振器随非线性阻尼系数的分岔情况。特别是在频率共振区域，考虑附加非线性阻尼的双稳态吸振器比线性阻尼的双稳态吸振器对主系统减振更有优势。

1 吸振器及主系统力学模型

本文提出的考虑非线性阻尼的双稳态电磁式振动吸振器及主系统的力学模型如图1所示。

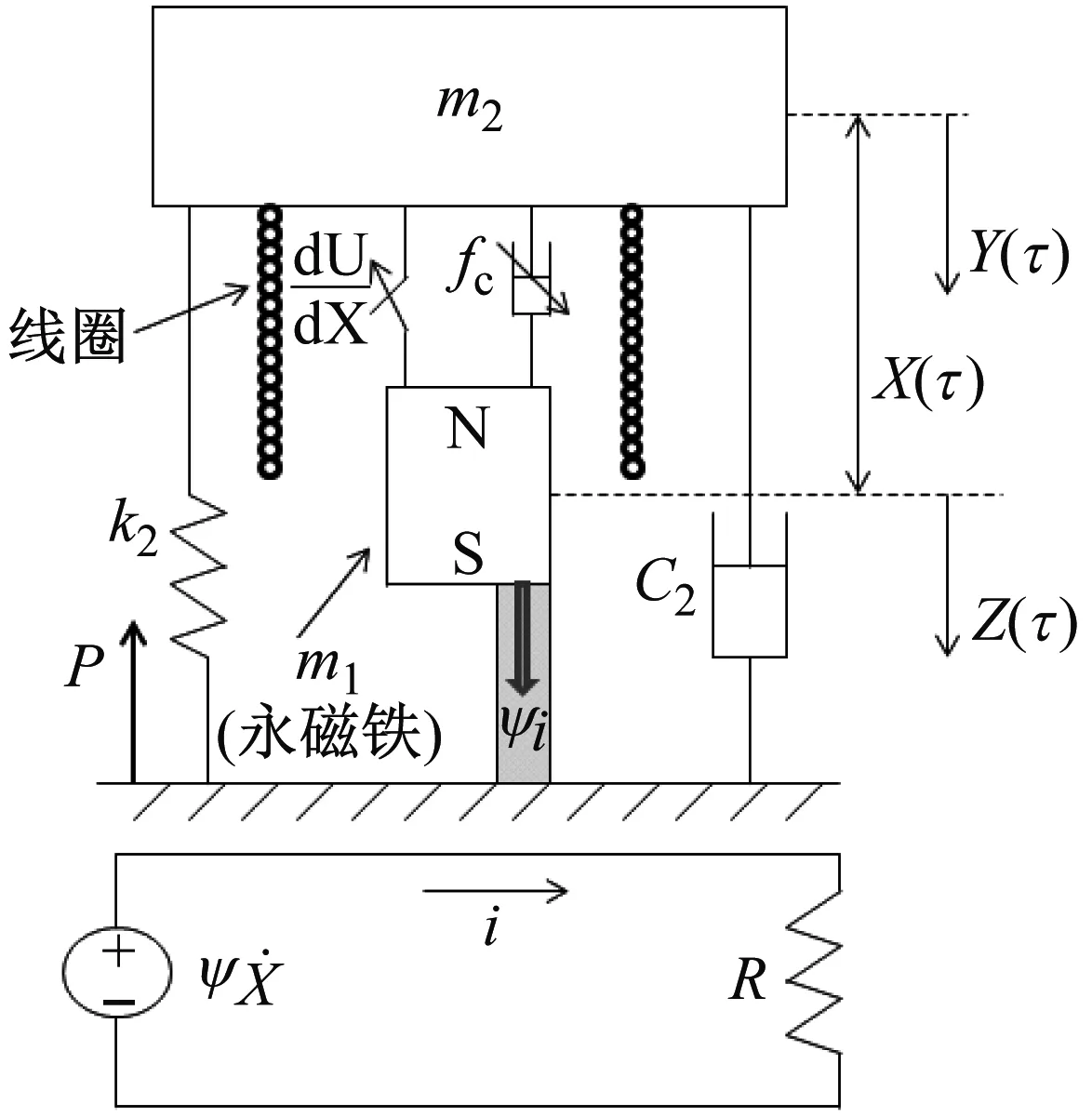
图1 考虑非线性阻尼的双稳态吸振器及主系统力学模型

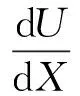
在该模型中，假设输出电路只有一个负载电阻R，i是电回路中的电流，ψ是机电耦合系数。简谐激励P施加给主质量后，主质量发生振动，进而吸振器吸收主质量的振动能量，吸振器发生振动，并与线圈发生相对运动X(τ)切割磁感线产生电动势，在能量收集电路中产生了电流i(τ)。

系统控制方程如下：

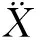
(1)

(2)

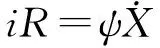
(3)

将式(3)代入式(1)，再对式(1)和式(2)进行无量纲化得到：

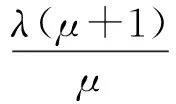
(4)

y″+γ2y′+y-μfγ1x′-λx′3+μf2x-μf2βx3=pcos (ωt)

(5)

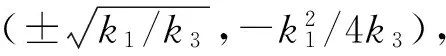
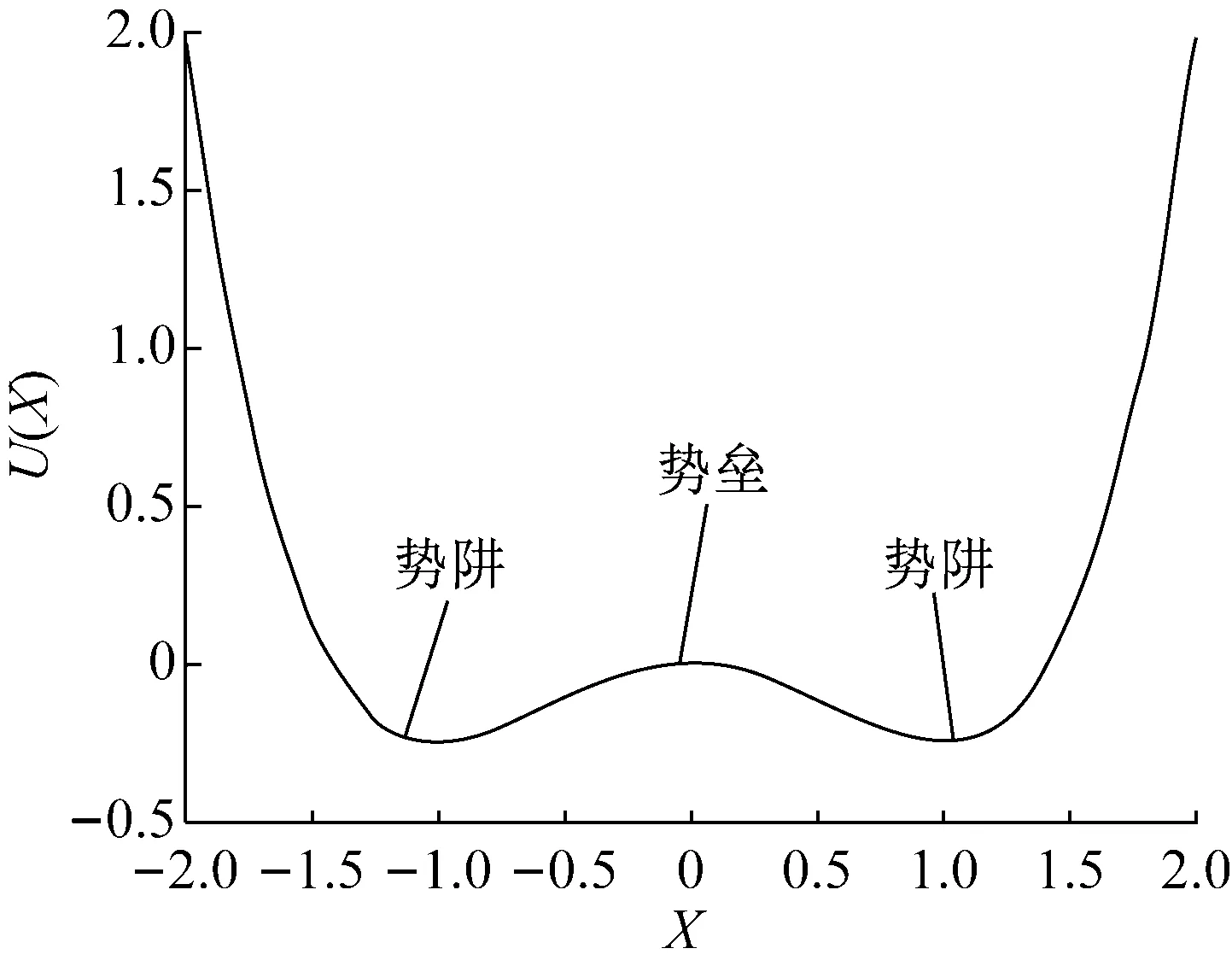
图2 双稳态势能函数示意图

2 振动能量及输出功率

减振效果主要表现在主系统的振动幅值及振动能量的大小，发电效果可用输出功率的大小来衡量。

非线性双稳态吸振器振动的能量包含两部分：动能和弹性势能，即：

(6)

同理，主系统振动的能量为

(7)

为了便于对比，在此采用平均振动能量表示，即：

(8)

(9)

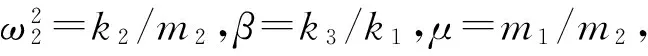
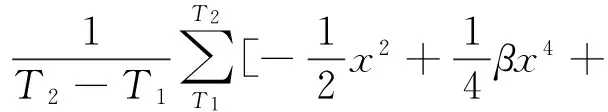
(10)

(11)

从式(10)可以看出，吸振器的能量取决于主系统和吸振器的位移和速度，由式(11)可知主系统的能量直接取决于主系统的位移和速度响应。

根据文献[16]，定义吸振器发电系统的平均输出功率为

(12)

式中：Pav为平均输出功率;T1和T2分别为初始和终止时刻;Δt为计算步长;n为T1和T2时间段内步长数。

某拟建桥梁总长约1520m，横跨既有高速公路，处在2km曲线段上，和既有高速公路成45°的夹角。根据实际情况，设计采用组合梁的形式直接跨越既有高速公路。组合梁的长度与高度分别为82m、9m，相邻节段之间的距离为10m，中心距为6.7m，采用不设竖杆的结构形式，整体呈三角形，上、下弦杆分别采用钢筋混凝土与预应力钢筋混凝土；上、下弦杆的截面形式分别为矩形与槽型。道床板采用40～45cm厚钢筋砼板，梁顶、底部宽度分别为9.4m、7.8m，梁端板总厚为90～95cm，梁体立面如图1所示。现围绕本工程实际情况，对其组合梁施工关键技术做如下深入分析。

由式(3)可知：

(13)

将式(13)代入式(12)中，得到

(14)

将ε2=ψ2/R代入式(14)，并令ω2=1得无量纲的吸振器平均输出功率：

(15)

由式(15)可知，当ε2为常数时，发电系统的平均输出功率与吸振器速度的平方成正比。

3 非线性阻尼与线性阻尼对主系统减振效果的比较

取参数f=0.25，μ=0.3，β=1.0，γ1=γ2=0.05，p

=0.15，ε=0.2，对无量纲式(4)和式(5)仿真计算，当吸振器分别采用线性阻尼和非线性阻尼时，共振下主系统的幅值——频率响应曲线和振动能量——频率响应曲线分别如图3(a)和(b)所示。

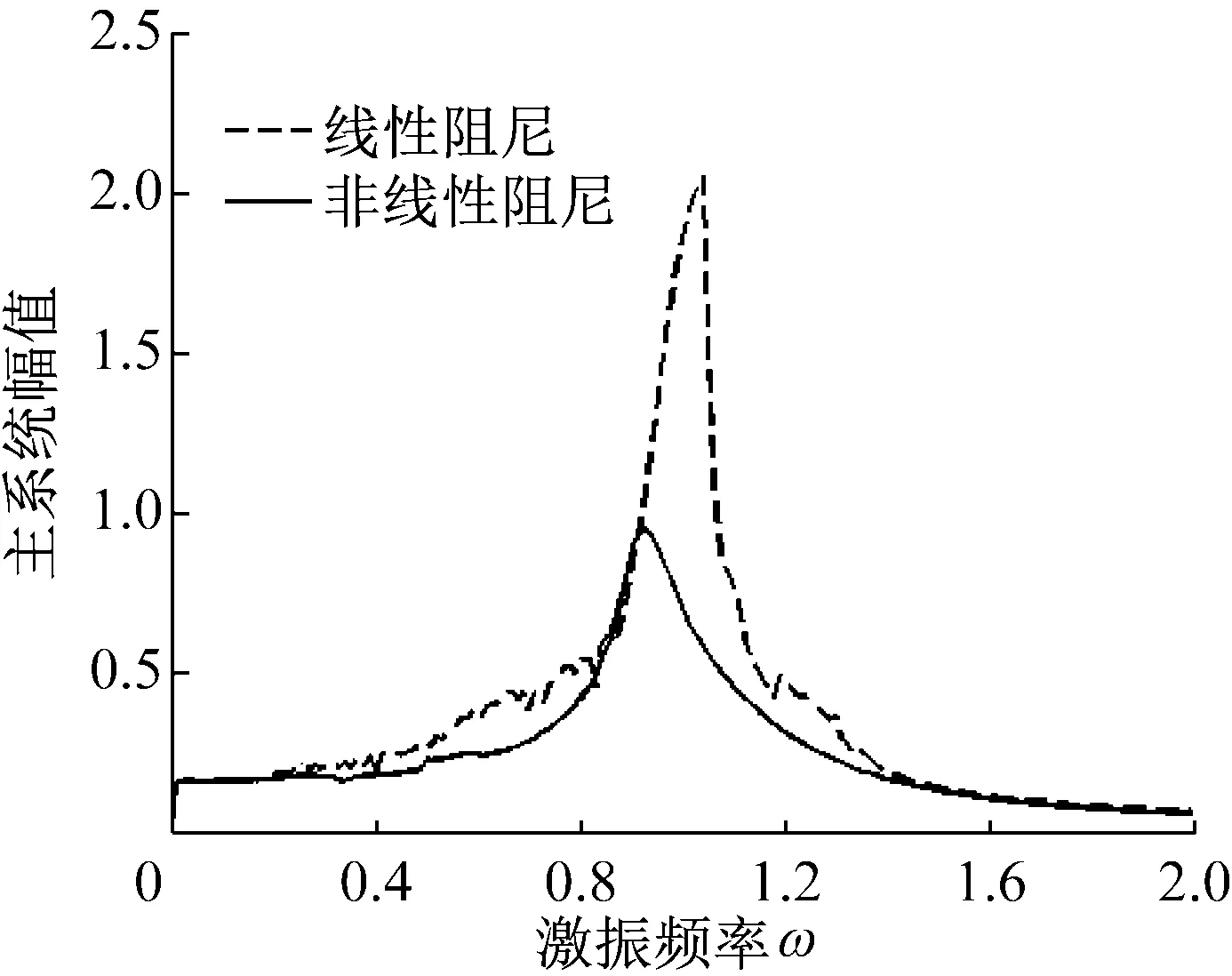
(a) 主系统幅频响应曲线

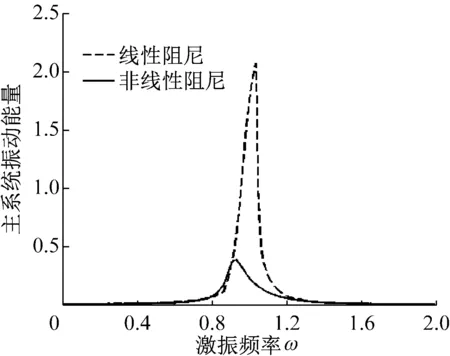
(b) 主系统能量随激励频率的响应曲线

Fig.3 Comparison of the effects of nonlinear damping and linear damping on the vibration reduction of the main system

从图3(a)主系统的幅频响应曲线可以看出，在共振区，双稳态吸振器采用非线性阻尼比线性阻尼时主系统振幅更小。图3(b)的振动能量曲线也反映出同样的变化趋势。

为了直观查看吸振器和主系统的振动情况，图4给出了共振下(ω=1.0)，分别考虑非线性阻尼和线性阻尼的双稳态吸振器影响下主系统的时域图、相图及振动能量响应。

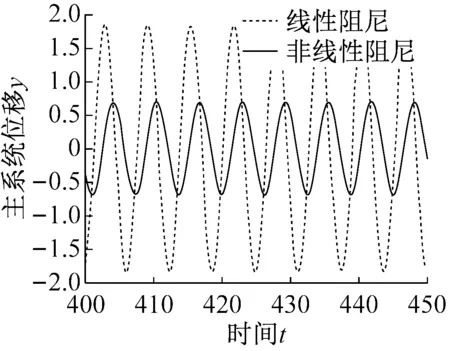
(a) 时域图

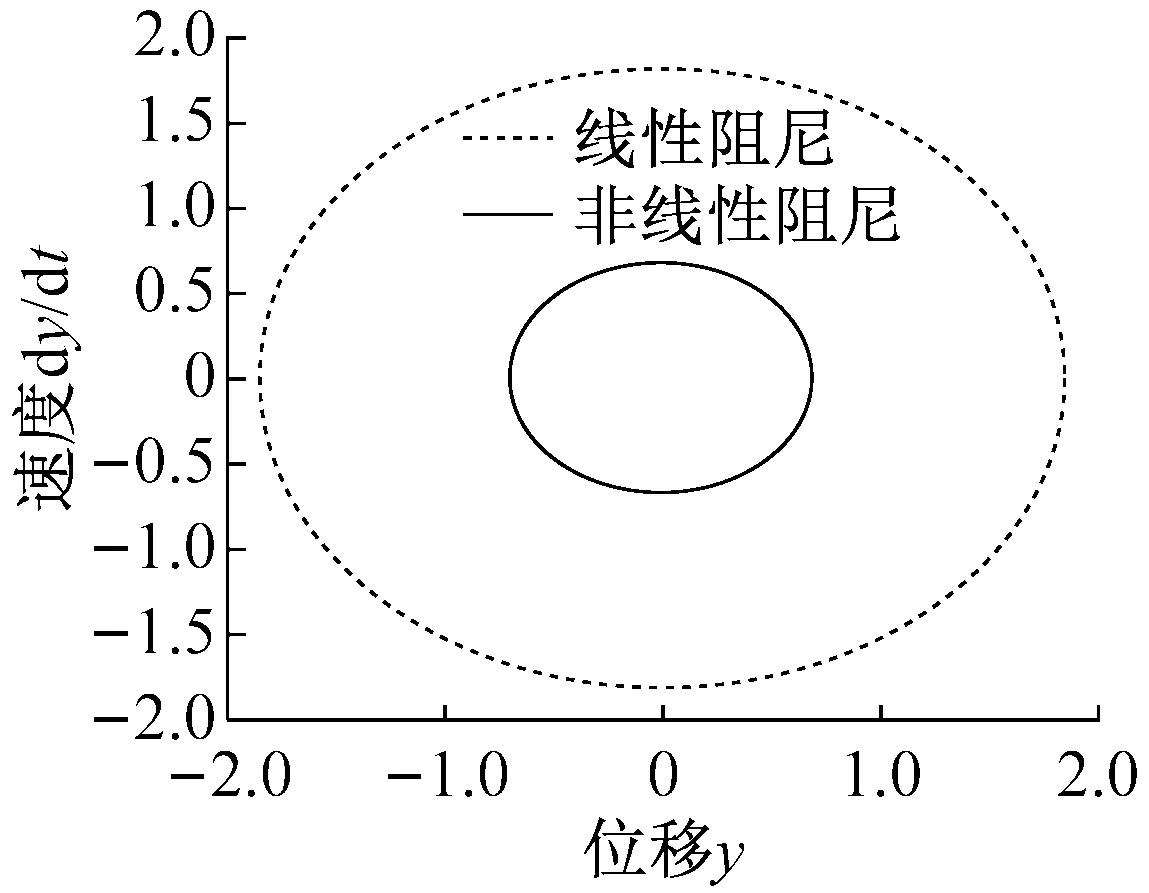
(b) 相图

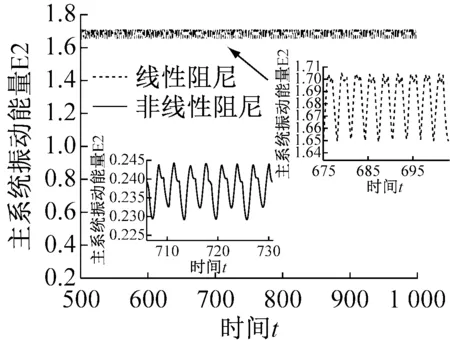
(c) 能量响应

4 非线性阻尼系数对双稳态吸振器的动力学特性影响

根据第3节的分析，主系统在共振区时，非线性阻尼对减振具有优越性，为了了解考虑非线性阻尼的双稳态吸振器的动力学特效，对其进行了以非线性阻尼系数为参数的分岔分析，分岔图如图5所示。取激振频率ω=1.0，其余参数为f=0.25，μ=0.3，β=1.0，γ1=γ2=0.05，p=0.15，ε=0.2。

从图5看出，在非线性阻尼系数处于[0-0.17]时，吸振器做大幅混沌或者周期运动，随着的增大，吸振器开始在平衡点1或-1处做小幅运动，偶尔出现平衡点间的跨越，大多数情况下在平衡点做小幅周期运动。

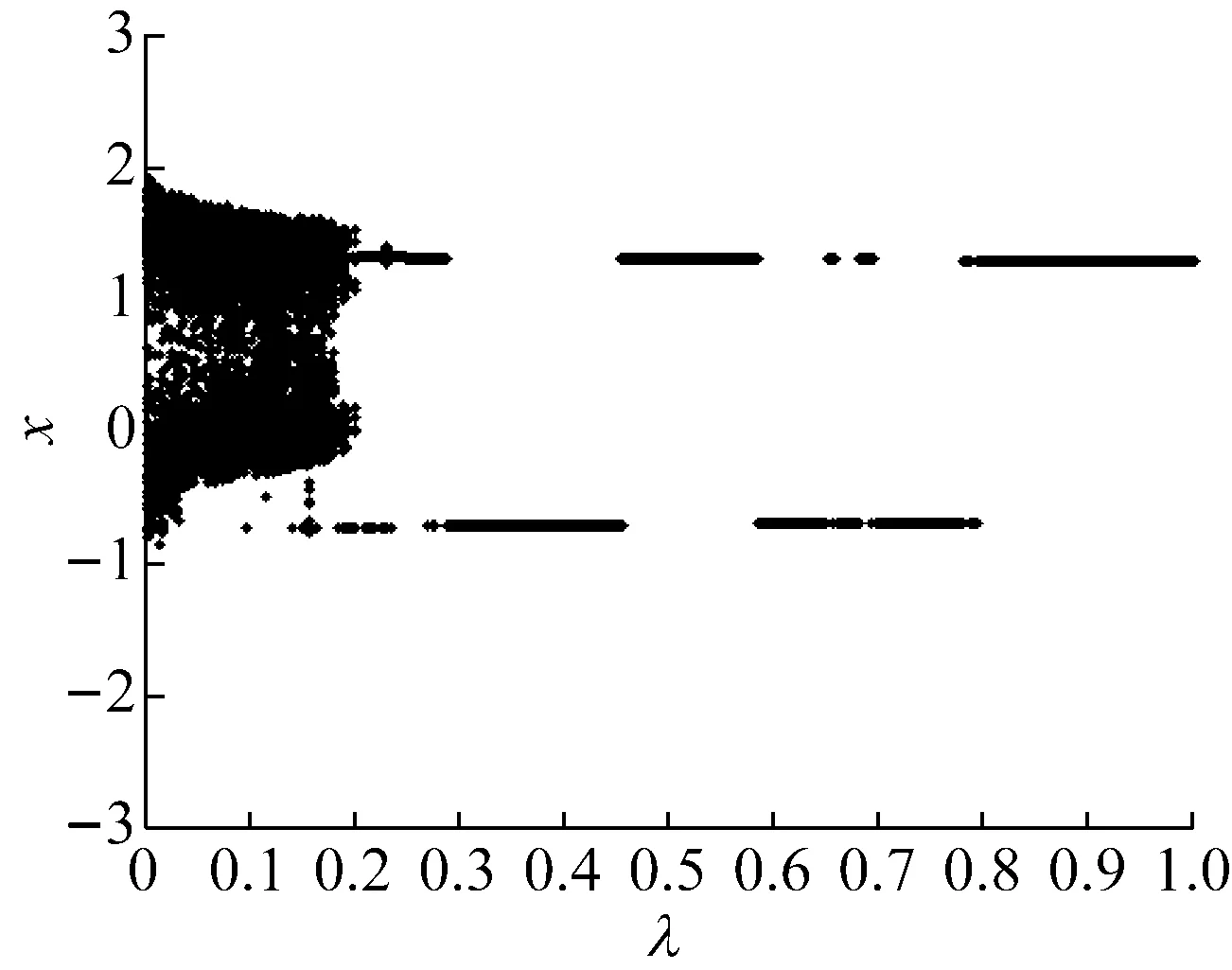
图5 以λ为分岔参数的分岔图

为了直观查看双稳态吸振器的动力学响应，图6和图7分别以λ=0.1和λ=0.9为例，给出了双稳态吸振器的时域图和相图。

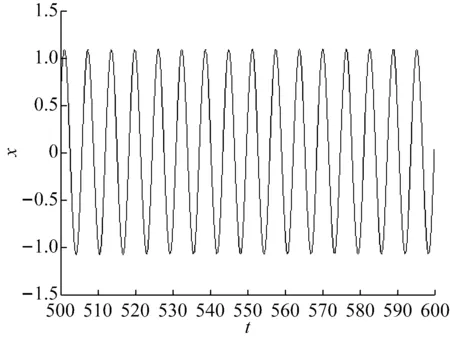
(a) 时域图

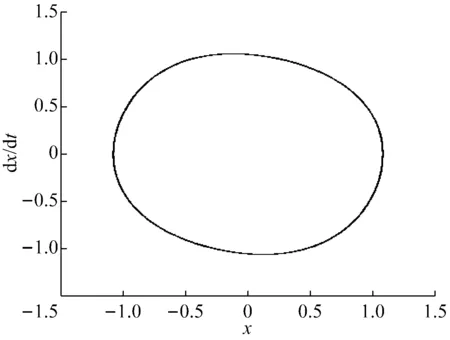
(b) 相图

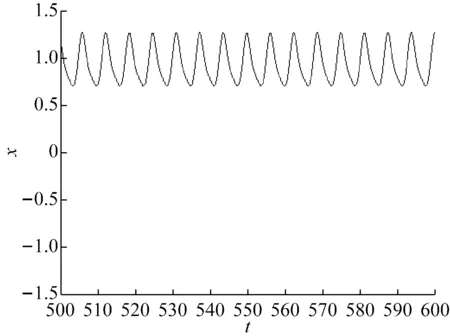
(a) 时域图

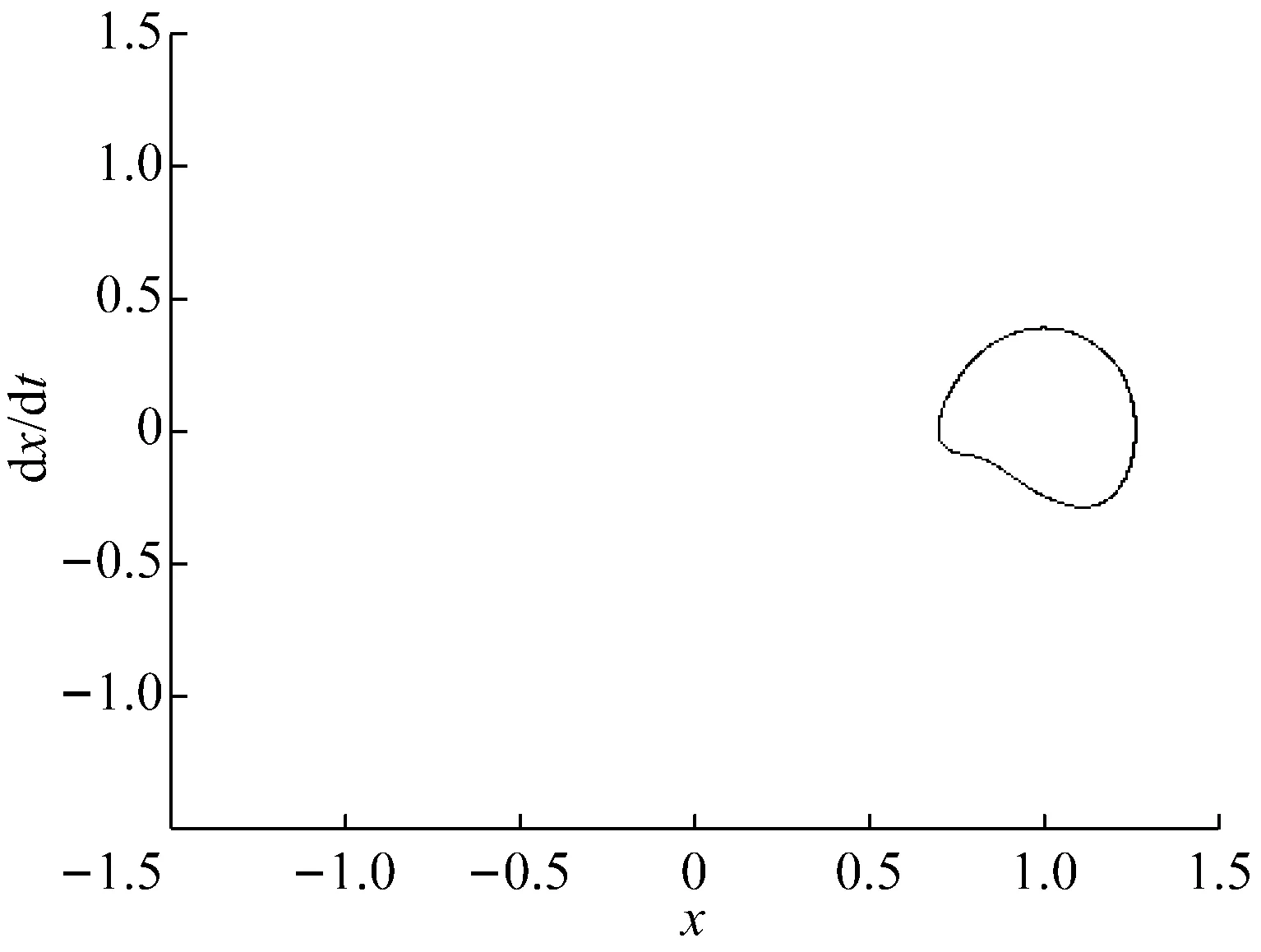
(b) 相图

从图6中可知，双稳态吸振器做大幅周期运动。

从图7可以看出，当增大λ=0.9时，双稳态吸振器在上平衡点做小幅周期运动。

5 非线性阻尼系数对减振和发电的影响

为了提高双稳态吸振器的工作效率，对非线性阻尼系数进行仿真分析。取参数f=0.25，μ=0.3，β=1.0，γ1=γ2=0.05，p=0.15，ε=0.2，不同的非线性阻尼系数λ对应的主系统平均振动能量E2av及吸振器平均输出功率Pav随激励频率ω的变化曲线,如图8所示。

从图8可知系统在频率共振区时，随着非线性阻尼系数λ的增大，主系统的平均振动能量E2av逐渐减小(图8(a))，吸振器的平均输出功率Pav也逐渐变小(图8(b))。在非共振区时，非线性阻尼的大小对主系统和吸振器都几乎没有影响。

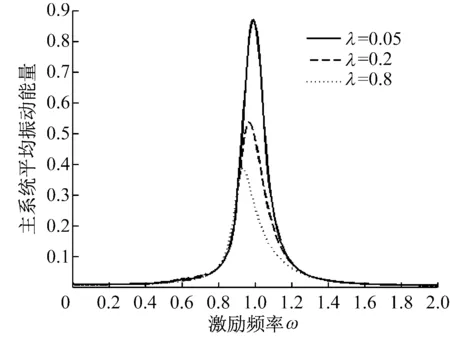
(a) 主系统平均振动能量

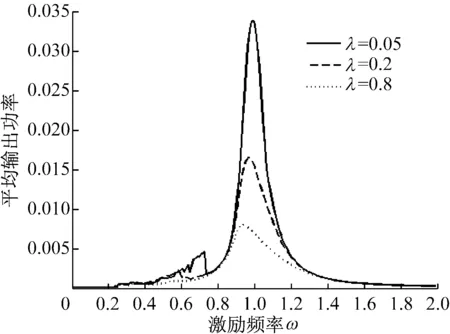
(b) 吸振器平均输出功率

图8 不同非线性阻尼系数下主系统平均能量和吸振器平均输出功率的变化曲线

Fig.8 The variation curves of average energy of the main system and average output power under different nonlinear damping coefficient

为了获取在频率共振区时非线性阻尼系数对主系统减振和吸振器振动能量的影响规律，现取共振激励频率ω=1.0，其余参数同上，主系统和吸振器的平均振动能量随非线性阻尼系数的变化曲线，如图9所示。

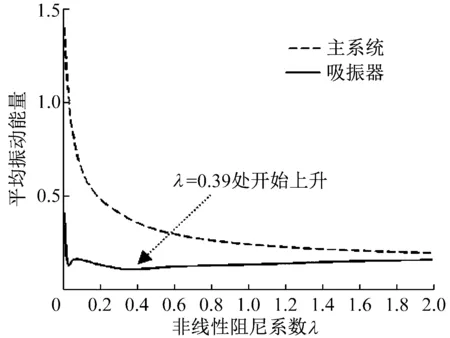
图9 频率共振区域下主系统和吸振器的平均能量随变化曲线

Fig.9 The average energy of the main system and the vibration absorber with the change of in the frequency resonance region

从图9中可以看出，在非线性阻尼系数较小时，主系统和吸振器的平均能量都较大，随着λ的增大，主系统平均能量E2av逐渐较小后保持平稳，吸振器E1av先减小后缓慢增大，在λ=0.39出现了拐点。

为了直观观察非线性阻尼对主系统和吸振器的能量影响，分别取λ=0.3和λ=1.8，对应的主系统及吸振器的振动能量随时间t的响应变化，如图10所示。

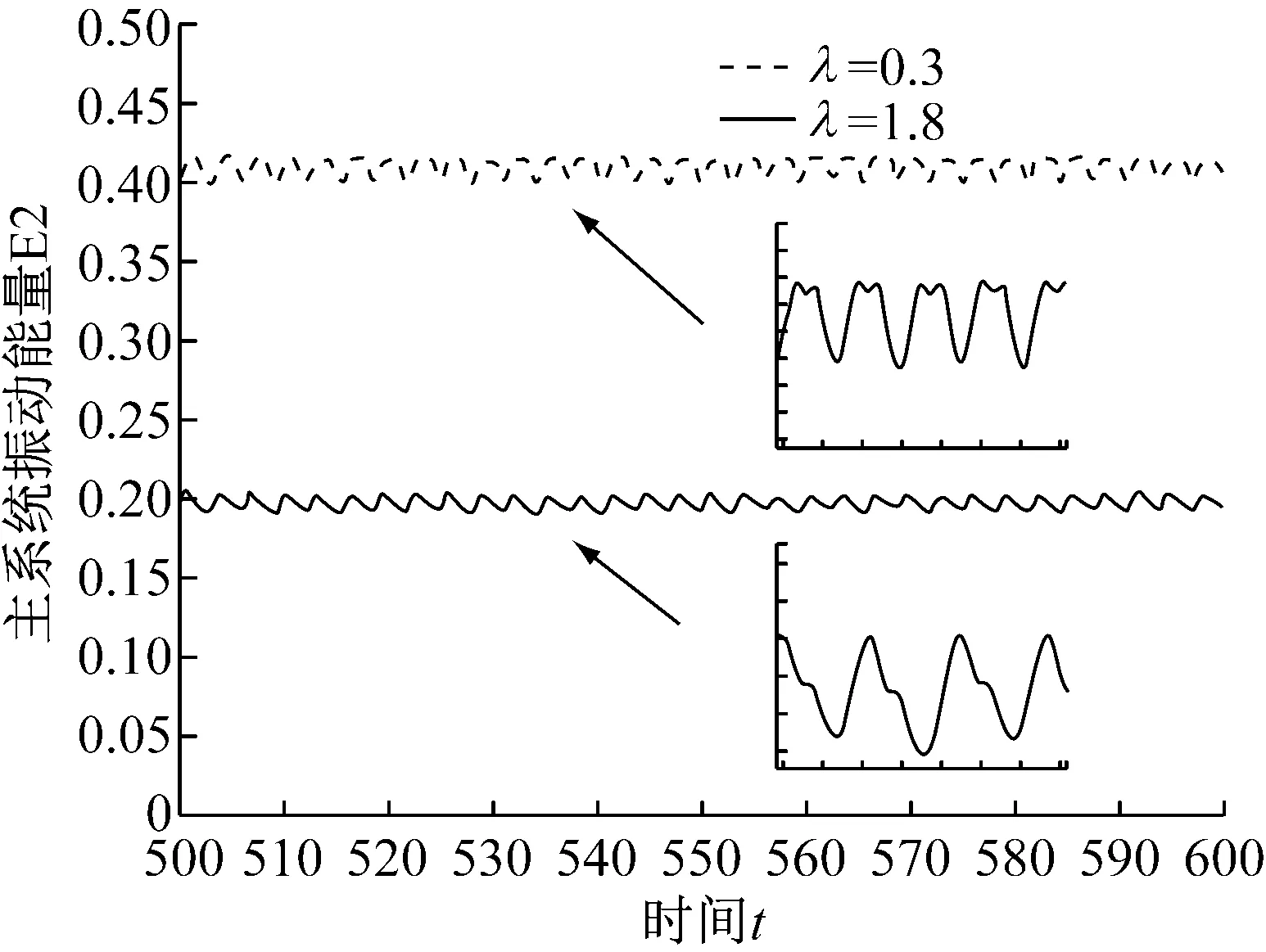
(a) 主系统振动能量响应

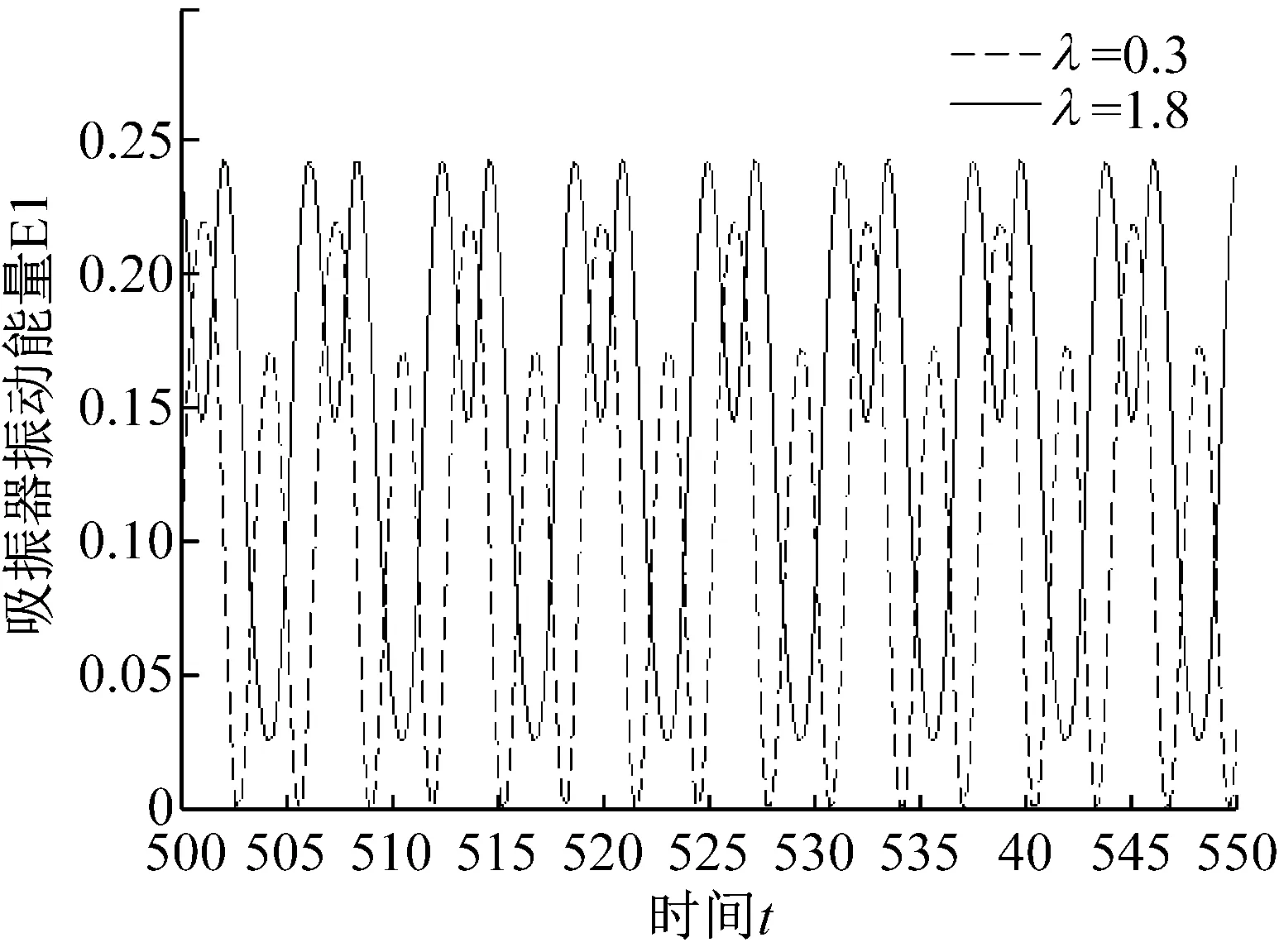
(b) 吸振器振动能量响应

从图10(a)可以看出λ=0.3时，主系统振动能量E2值位于0.4左右，当λ=1.8时，E2值减小到0.2左右，减振效果更佳。图10(b)给出了λ=0.3与λ=1.8时吸振器的振动能量对比，可以看出，后者的吸振器振动能量E2的最大值及最小值均大于前者，振动能量有所增大。

另外，为了进一步了解双稳态电磁吸振器在实现吸振同时的发电情况，图11给出为了吸振器平均输出功率随非线性阻尼系数变化的关系曲线。

从图11可以看出，吸振器的平均输出功率随着非线性阻尼系数的增加逐渐递减，也进一步验证了图8(b)的变化趋势。虽然图9中吸振器的振动能量随着非线性阻尼系数的增加出现了下降然后上升的趋势，但结合吸振器振动能量表达式(6)和平均输出功率表达式(14)可以看出，振动能量是位移和速度的函数，而平均输出功率仅仅是速度的函数。由于非线性阻尼的增大，吸振器振动的速度在减小。

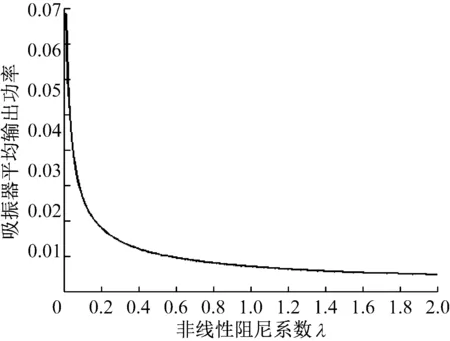
图11 吸振器平均输出功率随非线性阻尼系数变化的关系曲线

Fig.11 Relation curve of the average output power of vibration absorber and nonlinear damping

6 结 论

本文将非线性阻尼引入到双稳态电磁式振动能量捕获器中，提出了考虑非线性阻尼的双稳态吸振器，建立了主系统及吸振器系统力学和数学模型，借助数值仿真对比了考虑非线性阻尼的吸振器和考虑线性阻尼的吸振器对主系统减振效果，研究了频率共振时非线性双稳态吸振器随非线性阻尼的分岔特性，分析了非线性阻尼对主系统和吸振器的振动能量及平均输出功率的影响，主要结论如下：

(1) 考虑非线性阻尼的双稳态吸振器对主系统减振效果好于考虑线性阻尼的双稳态吸振器；

(2) 不同的非线性阻尼系数对应的双稳态吸振器的分岔效果不同，在较小时，吸振器会出现大幅运动，随着增大，吸振器在某一平衡点附近做小幅运动。

(3) 随非线性阻尼的增大，吸振器对主系统减振效果越明显，吸振器的振动能量先减小后缓慢增大，吸振器的平均输出功率呈现逐渐减小的趋势，也反映出虽然提高了减振效果，但也对吸振器产出的副产品——电量产生了影响。

[1] DENOYER K K, JOHNSON C D, DENOYER K K, et al. Recent achievements in vibration isolation systems for space launch and on-orbit applications[C]. International Astronautical Congress, 52ndTouhouse:2001.

[2] SUN W, GAO H, KAYNAK O. Adaptive backstepping control for active suspension systems with hard constraints[J]. IEEE/ASME Transactions on Mechatronics, 2013, 18(18):1072-1079.

[3] KOPIDAKIS G, AUBRY S, TSIRONIS G P. Targeted energy transfer through discrete breathers in nonlinear systems.[J]. Physical Review Letters, 2001, 87(16):175-196.

[4] PARSEH M, DARDEL M, GHASEMI M H. Investigating the robustness of nonlinear energy sink in steady state dynamics of linear beams with different boundary conditions[J]. Communications in Nonlinear Science & Numerical Simulation, 2015, 29(1/2/3):50-71.

[5] DAI H, ABDELKEFI A, WANG L. Usefulness of passive nonlinear energy sinks in controlling galloping vibrations[J]. International Journal of Non-Linear Mechanics, 2016, 81:83-94.

[6] XIONG H, KONG X, YANG Z, et al. Response regimes of narrow-band stochastic excited linear oscillator coupled to nonlinear energy sink[J]. 中国航空学报(英文版), 2015, 28(2):457-468.

[7] 陈俊, 董大伟, 时威振,等. 带子系统的动力包双层隔振系统隔振设计研究[J]. 振动与冲击, 2016, 35(16):211-218.

CHEN Jun, DONG Dawei, SHI Weizhen, et al. Study on vibration isolation design of double layer vibration isolation system with dynamic package of belt system[J]. Journal of Vibration and Shock,2016,35(16):211-218.

[8] 朱翔,殷学吉,李天云,等. 基于惯容器的动力反共振隔振器隔振特性分析[J].哈尔滨工程大学学报，2016，37(10):1318-1322.

ZHU Xiang, YIN Xueji, LI Tianyun, et al. Analysis of vibration isolation characteristics of dynamic anti resonance vibration isolator based on inertial container[J]. Journal of Harbin Engineering University, 2016，37(10):1318-1322.

[9] 宋春生, 于传超, 张锦光,等. 基于遗传算法的复杂双层磁悬浮精密隔振系统 LQR 控制研究[J]. 振动与冲击, 2016, 35(16):99-105.

SONG Chunsheng, YU Chuanchao, ZHANG Jinguang, et al. Study on LQR control of complex double magnetic levitation precision vibration isolation system based on genetic algorithm[J]. Journal of Vibration and Shock, 2016, 35(16):99-105.

[10] MILOVANOVIC Z, KOVACIC I, BRENNAN M J. On the displacement transmissibility of a base excited viscously damped nonlinear vibration isolator[J]. Journal of Vibration & Acoustics, 2009, 131(5):1749-1779.

[11] LANG Z Q, JING X J, BILLINGS S A, et al. Theoretical study of the effects of nonlinear viscous damping on vibration isolation of sdof systems[J]. Journal of Sound & Vibration, 2009, 323(1/2):352-365.

[12] JING X J, LANG Z Q. Frequency domain analysis of a dimensionless cubic nonlinear damping system subject to harmonic input[J]. Nonlinear Dynamics, 2009, 58(3):469-485.

[13] JING X J. Nonlinear characteristic output spectrum for nonlinear analysis and design[J]. IEEE/ASME Transactions on Mechatronics, 2013, 19(1):171-183.

[14] BRENNAN M J, TANG B, MELO G P, et al. An investigation into the simultaneous use of a resonator as an energy harvester and a vibration absorber[J]. Journal of Sound & Vibration, 2014, 333(5):1331-1343.

[15] KREMER D, LIU K. A nonlinear energy sink with an energy harvester: Transient responses[J]. Journal of Sound & Vibration, 2014, 333(20):4859-4880.

[16] 蓝春波, 秦卫阳. 带碰撞双稳态压电俘能系统的俘能特性研究[J]. 物理学报, 2015, 64(21):183-194.

LAN Chunbo, QIN Weiyang.Vibration energy harvesting from a piezo electric bistable system with two symmetric stops[J]. Acta Physica Sinica, 2015, 64(21):183-194.

Dynamiccharacteristicsofabi-stablestateelectromagneticvibrationabsorberconsideringnonlineardamping

LIU Lilan, REN Bolin, ZHU Guodong, YANG Qianqian

(School of Mechanical and Instrumental Engineering， Xi’an University of Technology， Xi’an 710048， Shaanxi， China)

Here, nonlinear damping was introduced into a bi-stable state electromagnetic vibration energy harvester. The harvester with nonlinear damping was proposed to be a nonlinear bi-stable state vibration absorber. The mechanical model for the absorber and the main system was established. The bifurcation diagram for the absorber vibration energy versus nonlinear damping parameter was obtained. Numerical simulation showed that the vibration reduction effect of the main system using a bi-stable state vibration absorber with nonlinear damping is superior to that with linear damping, especially, in the resonance region; furthermore, the relation curve between the vibration energy of the main system using the bi-stable state vibration absorber and nonlinear damping parameter is obtained; the influence laws of nonlinear damping on the vibration energy of the main system and its average output power are obtained. The results provided a reference for studying bi-stable state vibration absorbers.

nonlinear damping; bi-stable state vibration absorber; resonance; vibration energy; average power

国家自然科学基金(11572243)

2016-10-12 修改稿收到日期：2016-12-11

刘丽兰 女，副教授，硕士生导师，1979年12月生

O322

： A

10.13465/j.cnki.jvs.2017.17.015