利用向量的范数证明二元函数极值的充分条件

，

(东北林业大学 理学院，黑龙江 哈尔滨 150040)

利用向量的范数证明二元函数极值的充分条件

谭畅，马淑芳

(东北林业大学 理学院，黑龙江 哈尔滨 150040)

基于线性代数中向量范数的相关理论，给出二元函数极值的充分性定理的一个新的证明，此方法形式简明且便于理解。

二元函数；极值；充分条件；范数

一、定理证明的现行方法

二元函数取极值的充分性定理如下：

定理1 设二元函数f(x，y)在点P(x0，y0)的某邻域内存在二阶连续的偏导数，且fx(x0，y0)=0，fy(x0，y0)=0，记

A=fxx(x0，y0)，B=fxy(x0，y0)，C=fyy(x0，y0)

(1)若AC-B2>0，则f(x，y)在点P(x0，y0)取得极值，进一步地，当A>0时，取极小值；当A<0时，取极大值；

(2)若AC-B2<0，则f(x，y)在点P(x0，y0)不取极值；

(3)若AC-B2=0，则f(x，y)在点P(x0，y0)可能取极值，也可能不取极值。

许多教材，如菲赫金哥尔茨著《数学分析原理》[1]359中对二元函数极值充分条件的证明是充分且严格的，大致思想是将函数f(x，y)在点P(x0，y0)做二阶泰勒展开得：

f(x，y)-f(x0，y0)

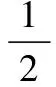
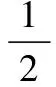
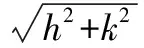
二、利用向量的范数证明定理

首先介绍一种向量的范数及范数的等价性定理。

定理2[10]142设‖·‖α和‖·‖β为Rn上任意两种范数，则存在正常数c1和c2，使得对一切向量X∈Rn有：

c1‖X‖β≤‖X‖α≤c2‖X‖β

下面给出本文定理的证明：

记

(1)若AC-B2>0，且A>0，则Q为对称正定矩阵，故

由范数的等价性，存在正常数c1和c2，使得：

c1ρ=c1‖X‖2≤‖X‖Q≤c2‖X‖2≤c2ρ

因此α1h2+2α2hk+α3k2=o(ρ2)。由此易知f(x，y)-f(x0，y0)的符号由Ah2+2Bhk+Ck2确定。当X≠0时，Ah2+2Bhk+Ck2=‖X‖Q2>0，f(x，y)-f(x0，y0)>0，故f(x，y)在点P(x0，y0)取得极小值。

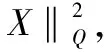
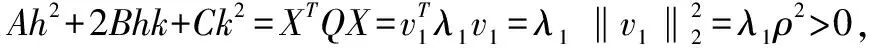
(3)若AC-B2=0，函数z=x3+y3及z=x4+y4在点(0，0)均满足AC-B2=0，(0，0)是后者的极值点，但不是前者的极值点。证毕。

三、结论

基于线性代数中向量范数的相关知识给出了二元函数取极值充分性定理的一个新的证明，所用的方法可以帮助学生灵活运用各科知识，拓宽解决问题的思路。相较于经典的分析方法，此方法更为直接而且形式简明。

[1]菲赫金哥尔茨.微积分教程[M].路可见，余家荣，吴亲仁译.北京：高等教育出版社，1959.

[2]刘玉琏，傅沛仁.数学分析讲义(下册)[M].北京：高等教育出版社(第5版)，2008.

[3]李国莹.多元函数极值充分条件的证明[J].中国大学教学，1987，(5)：42—44.

[4]张家琏，宋述刚.关于二元函数极值存在的充分性定理的证明[J].荆州师专学报(自然科学版)，1990，(2)：18—20.

[5]王敏芝.关于多元函数的极值判别准则[J].浙江理工大学学报，2007，24(5)：83—87.

[6]王欣.二元函数极值充分条件的证明及条件极值的判定[J].沈阳大学学报(自然科学版)，1996，(2)：82—85.

[7]汪全珍.多元函数极值判别法的一个证明[J].高等数学研究[J]，2009，12(2)：39—40.

[8]郭常予，徐玲等.多元函数极值问题的分析与研究[J].中国科技论文在线精品论文.2009，2(1)：6—10.

[9]吴海玉，冯志刚.多元函数极值充分性定理的另一证明[J].甘肃联合大学学报(自然科学版)，2010，24(6)：7—9.

[10]徐树芳，高立，张平文.数值线性代数[M]. 北京：北京大学出版社，2013.

AProofofSufficientConditionforExtremumofBinaryFunctionbyUsingVectorNorm

TAN Chang，MA Shu-fang

(College of Science，Northeast Forestry University，Harbin150040， China)

Based on the theory of vector norm in linear algebra， a new proof ofsufficient condition for the extremum of binary functionis is given， which is simple and easy to understand.

binary function；extremum；sufficient condition；norm

O171

：A

：1008-6714(2017)09-0085-02

〔责任编辑：李海波〕

10.3969/j.issn.1008-6714.2017.09.038

2017-05-02

东北林业大学教育教学研究项目(DGY2016-45)

谭畅(1982—)，女，吉林吉林人，讲师，博士研究生，从事计算机代数教学研究。