散货船配载仪中完整稳性计算方法研究

王 智 洲， 孙 霄 峰， 尹 勇， 刘 春 雷

( 大连海事大学 航海动态仿真与控制交通部重点实验室， 辽宁 大连 116026 )

散货船配载仪中完整稳性计算方法研究

王 智 洲， 孙 霄 峰*， 尹 勇， 刘 春 雷

( 大连海事大学 航海动态仿真与控制交通部重点实验室， 辽宁 大连 116026 )

为提高散货船配载仪中完整稳性计算精度，基于船舶三维设计数据对完整稳性进行了计算．首先通过对三维设计模型切片得到每个肋位处横剖面型值数据；然后对横剖面型值数据进行等距偏移模拟板厚，得到各肋位处的外板数据；再通过水线面与外板数据求交计算该浮态下的船舶参数；最后按照不同完整稳性计算方法计算复原力臂，绘制出不同载况下的船舶复原力臂曲线．以38 300 t散货船RUI AN CHENG为例，分别采用固定纵倾法和自由纵倾法对其3个典型载况进行实例计算．结果表明，采用静平衡下的自由纵倾法与NAPA计算结果更为接近，复原力臂平均误差为0.003 7 m，最大误差为0.009 4 m，验证了基于三维设计数据进行完整稳性计算的准确性及可行性．

船舶完整稳性；散货船；配载仪；NAPA软件

0 引 言

船舶在外力作用下偏离其平衡位置而倾斜，当外力消失后，能自行恢复到原来平衡位置的能力，叫作船舶稳性[1]．船舶完整稳性是船舶最主要的航行性能之一，是确保船舶安全航行的基本保障．

目前散货船完整稳性计算分为两种．一是固定纵倾计算法：船舶在横倾过程中(给定横倾角，一般取0°～60°)，保持纵倾角始终不变，只有船舶吃水改变，使得船舶横倾后的排水量与初始状态下的排水量相等．二是自由纵倾计算法：船舶在横倾过程中会自由纵倾，吃水和纵倾角都会变化．现有自由纵倾下的稳性计算法分为两类：第一类是静平衡下的自由纵倾法，该方法保证在船舶到达指定横倾角时，合力以及合力矩为0[2-3]；第二类是基于最小功原理的自由纵倾法(简称最小功计算法)，该方法保证船舶到达指定横倾角时船舶位能最小[4-5]，可以用牛顿迭代法[4，6-8]或者优化法[9]等进行求解．

目前国际上的散货船配载仪软件，如韩国HANLA IMS公司开发的LOADPLUS和德国SEACOS 公司开发的MACS3都实现了基于三维设计模型的船舶完整稳性计算，但是由于商业保护等原因，其计算方法并未公开．国内的配载仪对稳性的计算大多基于静水力数据，基于三维设计模型开发的配载仪软件较少．因此，本文基于船舶三维设计数据，对散货船配载仪中完整稳性计算方法进行研究．

1 船舶三维设计数据库建立

本文通过对船舶型表面三维设计模型沿船长方向依次切片，得到船舶每个肋位处横剖面的型值数据，如图1所示．考虑到船壳板的存在，需要对船舶每个横剖面进行大小为平均板厚的等距偏移，得到外板数据，具体的过程参考文献[10]．规定x轴船艏方向为正，y轴左舷方向为正，z轴基平面向上为正．

图1 散货船RUI AN CHENG型表面切片示意图

2 稳性计算

船舶完整稳性的计算基于以下几个假设[2]：

(1)横倾力矩水平恒定作用在船上，船舶等容横倾且重心不变；

(2)横倾力矩在空间中的位置恒定；

(3)回复力矩仅由重力和浮力组成．

设船舶浮心坐标为b(xb，yb，zb)，重心坐标为g(xg，yg，zg)；横倾角为θ，纵倾角为φ，kn为船舶基点到浮力作用线的垂直距离，kg为重心的垂直距离：

kn=yb×cosθ+zb×sinθ

(1)

设船舶排水量为Δ，Mf为自由液面惯性矩与密度的乘积，dgz为自由液面修正量：

dgz=∑Mf×sinθ/Δ

(2)

船舶完整稳性复原力臂gz可表示为

gz=kn-kg×sinθ-dgz-yg×cosθ

(3)

2.1 固定纵倾法

船舶由初始浮态横倾到指定角度，稳性计算可转化为保持横倾角与纵倾角不变，变化吃水使函数t最小的问题．设船舶重力为G，海水密度为ρ，当前水线面下船舶排水量与船舶重力的差值为

t=ρV-G

(4)

其中V为当前水线面下船舶的排水体积．

吃水增量

dt=(G-ρV)/w

(5)

其中w为当前船舶的水线面面积．

当满足函数t小于设定精度时，即可求出当前横倾角下的吃水．

2.2 自由纵倾法

按照文献[4]，引用下列符号：

(6)

2.2.1 静平衡下的自由纵倾法 在已知船舶初始排水量和重心位置下，将船舶横倾角设置为目标横倾角，变化船舶吃水和纵倾角φ，保持横倾角θ不变，船舶满足平衡方程组：

f1=ρV-G=0
f2=Myz+Mxytanφ=0

(7)

引入向量表示：

(8)

其中Tm为船舯吃水．

使用牛顿法得到线性化方程：

F′(xk)Δxk+F(xk)=0；k=0，1，2，…

(9)

解线性方程组：

(10)

其中δTmk、δtanφk为设置精度．

按照船舶静力学原理，式(7)的雅可比矩阵为

其中S为水线面在基平面上投影的面积；船舶漂心坐标为f(xf，yf，zf)；水线面面积S对通过该水线面漂心f横轴的纵向惯性矩为Ilf．

2.2.2 最小功计算法 船舶在倾斜过程中将找到位能最小的位置．最小功计算法为在初始浮态的基础上横倾，通过引入最小功原理建立优化模型．通过解析优化算法确定倾斜船舶功的极值从而计算船舶稳性，具体的算法见文献[4]．

2.3 程序设计

本文用C++语言编写了船舶完整稳性计算程序．最小功计算法的程序最复杂，本文采用牛顿迭代法进行求解，流程图如图2所示．首先对所有切割肋位处的横剖面进行等距偏移得到外板的离线数据；然后由船舶初始浮态得到船舶初始船舯吃水、横倾角及纵倾角，从而确定初始水线面；再依次与水线面求交得到水线面数据和水下部分横剖面数据；进而可以求解雅可比矩阵所需的静水力参数．其他稳性计算法的流程与此类似，这里不再详述．

图2 稳性计算流程图

3 算 例

以散货船RUI AN CHENG为例，平均板厚0.019 m．以不同的完整稳性算法计算表1中的典型载况，计算区间为0°～60°．根据计算结果绘制复原力臂曲线，并与NAPA计算值进行比较．

表1 典型载况

NAPA公司开发的软件是目前造船界应用最为广泛的船舶设计软件[11]．目前大约有32个国家，总计320多家单位采用NAPA软件作为船舶方案设计和技术设计的主要工具．NAPA公司的配载软件已经成为了行业的标杆，挪威船级社(DNV GL)、英国劳氏船级社(LR)等在进行配载仪认可时，均将送测配载仪与NAPA配载软件的计算结果进行对比，根据计算结果误差是否符合要求确认是否颁发相应认可．

本文选取空船、压载出港、均质货满载出港3个典型载况进行稳性计算对比．其他载况如不均匀装载等极端载况，对船舶强度的影响较大，但由于该种载况只影响了重心位置，对完整稳性计算的影响不大．

3.1 固定纵倾法

通过固定纵倾法绘制的复原力臂曲线与NAPA计算曲线对比如图3～5所示，L为复原力臂．

图3 空船复原力臂曲线对比1

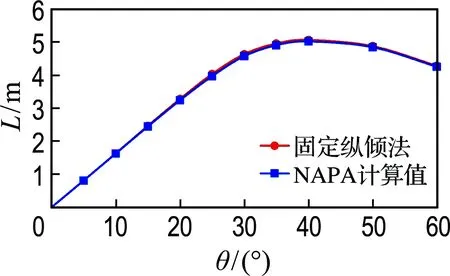
图4 压载出港复原力臂曲线对比1

图5 均质货满载出港复原力臂曲线对比1

Fig.5 Righting arm curves comparison in fully loaded with homogeneous cargo at departure condition 1

3个载况下的平均误差如图6所示，载况1的平均误差为-0.015 m，最大误差为0.080 m；载况2的平均误差为0.030 m，最大误差为-0.064 m；载况3的平均误差为0.017 m，最大误差为-0.044 m．

图6 复原力臂误差曲线1

3.2 静平衡下的自由纵倾法

通过静平衡下的自由纵倾法绘制的复原力臂曲线与NAPA计算曲线对比如图7～9所示．

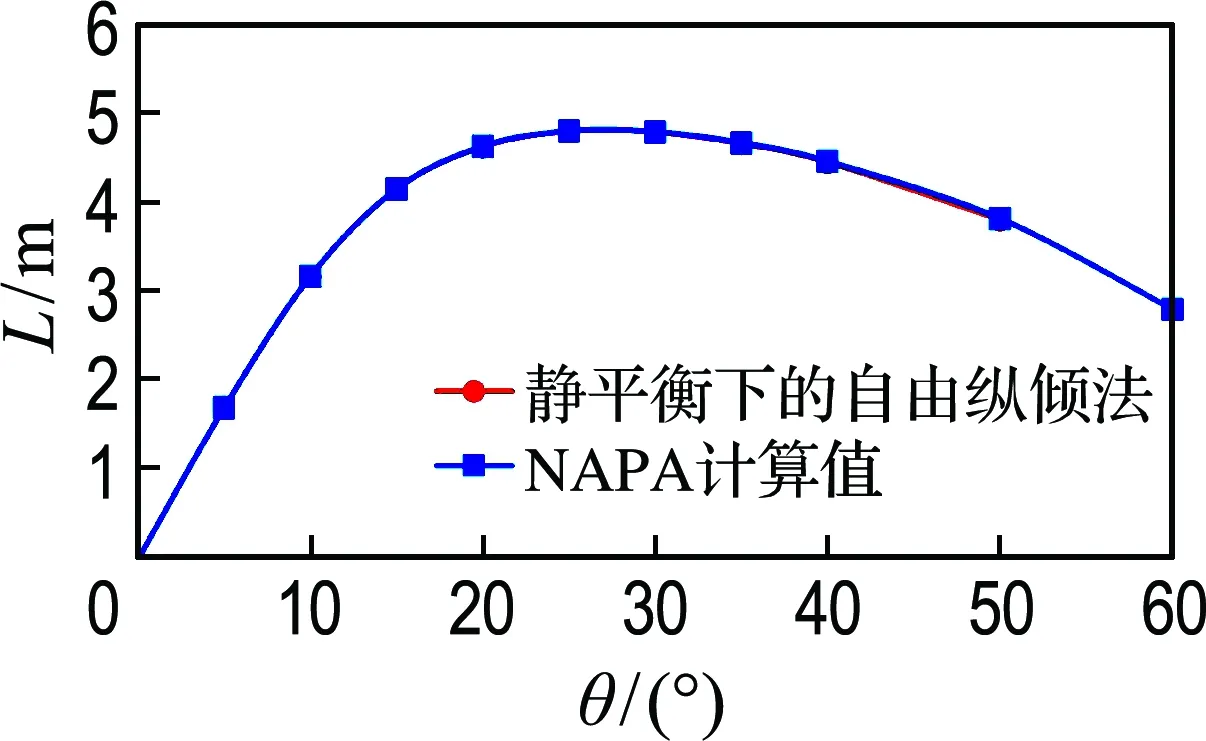
图7 空船复原力臂曲线对比2

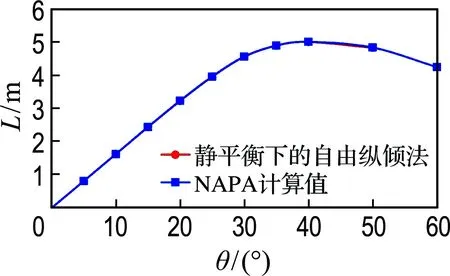
图8 压载出港复原力臂曲线对比2

图9 均质货满载出港复原力臂曲线对比2

Fig.9 Righting arm curves comparison in fully loaded with homogeneous cargo at departure condition 2

3个载况下的平均误差如图10所示，载况1的平均误差为0.004 6 m，最大误差为0.009 4 m；载况2的平均误差为0.003 5 m，最大误差为0.006 3 m；载况3的平均误差为0.003 7 m，最大误差为0.005 7 m．

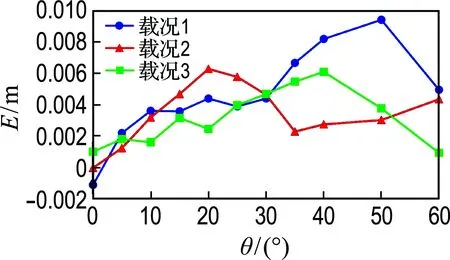
图10 复原力臂误差曲线2

3.3 最小功计算法

通过基于最小功原理的自由纵倾法绘制的复原力臂曲线与NAPA计算曲线对比如图11～13所示．

3个载况下的平均误差如图14所示，载况1的平均误差为0.406 m，最大误差为0.860 m；载况2的平均误差为0.190 m，最大误差为0.510 m；载况3的平均误差为-0.049 m，最大误差为-0.320 m．可以看到，随着角度增大，NAPA计算值与最小功计算法的差距在逐渐增大，在60°时，差距最大达到了0.860 m．

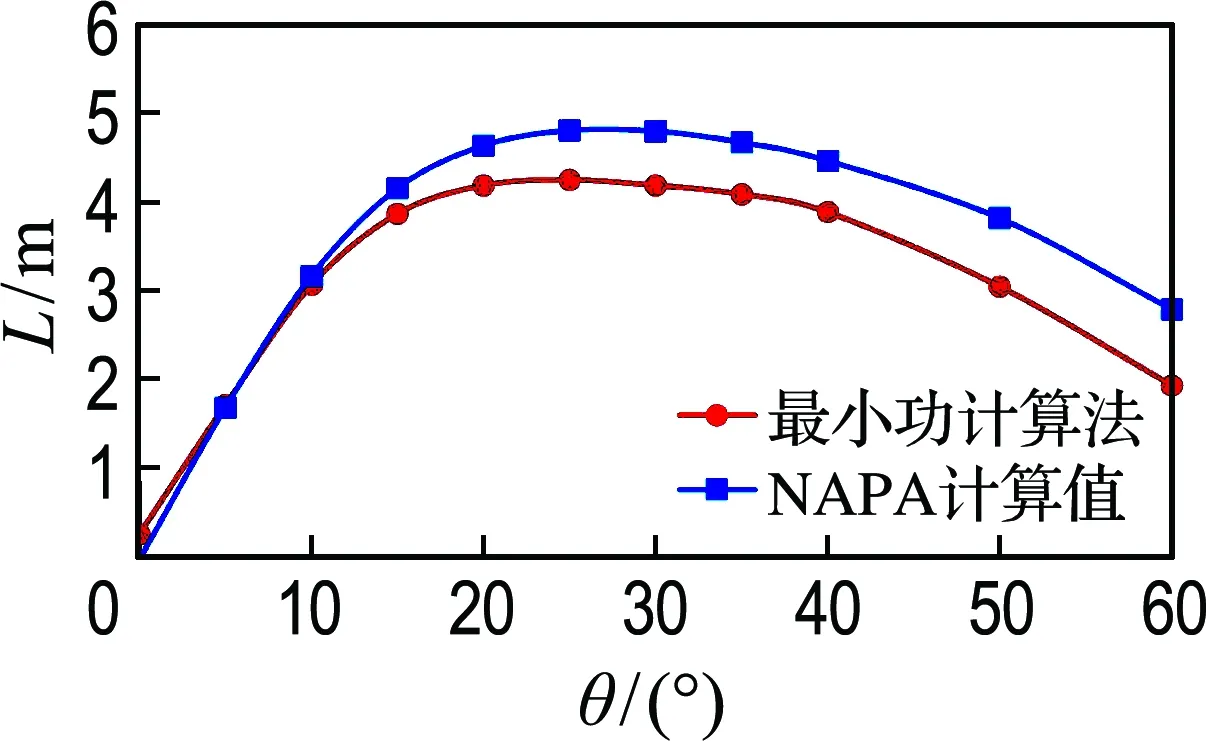
图11 空船复原力臂曲线对比3

图12 压载出港复原力臂曲线对比3

图13 均质货满载出港复原力臂曲线对比3

Fig.13 Righting arm curves comparison in fully loaded with homogeneous cargo at departure condition 3

图14 复原力臂误差曲线3

3.4 实验结果

挪威船级社和英国劳氏船级社对采用三维设计模型计算的散货船配载仪中复原力臂的计算误差要求为最大5 cm或者5%．

(1)与NAPA计算值相比，对于散货船这种艏艉差异不大的船型，使用固定纵倾法计算载况的平均误差不是很大，但最大误差达到了0.080 m，不满足船级社的精度要求，说明该方法不适合配载仪软件的稳性计算．

(2)使用静平衡下的自由纵倾法，可以取得和NAPA计算值非常接近的结果，3个载况下最大误差为0.009 4 m，达到了很高的精度，满足了船级社的精度要求．并且该方法的实时性很好，每个载况不同横倾角的迭代次数如图15所示，平均每个横倾角迭代2～4次可以得到结果，满足配载仪实时性的要求．

图15 各横倾角下迭代次数

(3)使用最小功计算法计算差别较大，最大误差达到了0.860 m．说明NAPA不是按照最小功原理进行稳性计算的．由于该方法不保证横倾之后纵向力矩的平衡，导致了计算结果的差异．理论上讲，采用最小功计算法比较符合船舶横倾过程中稳性变化的实际情况．

根据本文的研究结论，使用静平衡下的自由纵倾法进行稳性模块的开发，成功完成了基于三维设计数据的散货船配载仪软件设计，如图16所示．该配载仪已通过CCS认可，并已成功装船．

图16 散货船配载仪主界面

4 结 论

(1)船舶三维型表面模型来源于船舶设计软件，采用船舶真实数据，计算精度较高；

(2)对固定纵倾和自由纵倾下稳性计算结果与NAPA计算值进行比较，分析结果表明采用静平衡下的自由纵倾法与NAPA计算值更为接近；

(3)不同的稳性计算软件使用的方法不同，计算出的复原力臂会有所不同，应该根据实际情况选择相应的计算方法；

(4)本文虽然以散货船为例进行了完整稳性计算，但对于油船、集装箱船等配载仪和船舶设计软件中的稳性模块开发具有一定的指导意义．

[1] 盛振邦,刘应中. 船舶原理[M]. 上海:上海交通大学出版社, 2003.

SHENG Zhenbang, LIU Yingzhong.ShipPrinciple[M]. Shanghai: Shanghai Jiao Tong University Press, 2003. (in Chinese)

[3] 于雁云,林 焰,纪卓尚. 海洋平台拖航稳性三维通用计算方法[J]. 中国造船, 2009,50(3):9-17.

YU Yanyun, LIN Yan, JI Zhuoshang. General algorithm to calculate the towing stability of the platform [J].ShipbuildingofChina, 2009,50(3):9-17. (in Chinese)

[4] 赵晓非,蔡伟科. 船舶稳性计算优化方法研究[J]. 中国造船, 1987(2):86-92.

ZHAO Xiaofei, CAI Weike. An optimization method for the calculation of ship stability curves [J].ShipbuildingofChina, 1987(2):86-92. (in Chinese)

[5] 崔 阳. 基于CATIA三维建模的船舶稳性计算方法研究[D]. 大连: 大连理工大学, 2015.

CUI Yang. Research on the calculation method of ship stability based on 3D modeling with CATIA [D]. Dalian: Dalian University of Technology, 2015. (in Chinese)

[6] 桑 松,徐学军. 浮式结构物完整稳性优化计算原理[J]. 上海交通大学学报, 2009,43(10):1568-1572. SANG Song, XU Xuejun. Optimization calculational principle on intact stability of floating structures [J].JournalofShanghaiJiaotongUniversity, 2009,43(10):1568-1572. (in Chinese)

[7] 孙承猛,刘寅东. 一种船舶最小稳性和自由浮态计算的改进算法[J]. 中国造船, 2007,48(3):1-4.

SUN Chengmeng, LIU Yindong. An improved algorithm for calculating ship′s minimum stability and free floatation [J].ShipbuildingofChina, 2007,48(3):1-4. (in Chinese)

[8] 赵成璧,邹早建. 船舶稳性计算程序ESTAB[J]. 武汉造船, 2001(2):12-15.

ZHAO Chengbi, ZOU Zaojian. ESTAB-a computer package for stability calculation of ships [J].WuhanShipbuilding, 2001(2):12-15. (in Chinese)

[9] 马 坤,张明霞,纪卓尚,等. 非线性规划法计算船舶稳性[J]. 中国造船, 2003,44(2):83-86.

MA Kun, ZHANG Mingxia, JI Zhuoshang,etal. Application of nonlinear programming to calculation of ship stability curve [J].ShipbuildingofChina, 2003,44(2):83-86. (in Chinese)

[10] 王智洲,孙霄峰,尹 勇,等. 基于三维设计数据的船舶湿面积计算[J]. 船舶工程, 2016,38(5):5-8,73. WANG Zhizhou, SUN Xiaofeng, YIN Yong,etal. Ship′s wetted surface calculation based on 3D design data [J].ShipEngineering, 2016,38(5):5-8,73. (in Chinese)

[11] 蔡计强,谌志新. 基于NAPA软件的渔业船舶完整稳性分析[J]. 渔业现代化, 2016,43(1):41-46.

CAI Jiqiang, CHEN Zhixin. Analysis on the intact stability of the fishing vessel based on NAPA software [J].FisheryModernization, 2016,43(1):41-46. (in Chinese)

Studyofcalculationmethodofintactstabilityinbulkcarrierloadingcomputer

WANG Zhizhou, SUN Xiaofeng*, YIN Yong, LIU Chunlei

( Key Laboratory of Marine Dynamic Simulation & Control for Ministry of Communications, Dalian Maritime University, Dalian 116026, China )

For better computational accuracy of intact stability in bulk carrier loading computer, intact stability is calculated based on ship 3D design data. First, moulded data of transverse sections in each frame are obtained by 3D design model slicing. Then, the shell data in each frame are gained by equidistant offsetting of transverse moulded data to simulate shell thickness. After that, ship parameters in this floating condition are gained by intersecting water plane and shell data. Finally, righting arms are calculated using different intact stability calculation methods and the ship righting arm curves in different loading conditions are plotted. Three typical loading conditions of 38 300 t bulk carrier RUI AN CHENG are selected for calculation using fixed trim and free trim methods. The result shows that the computation result using static equilibrium free trim method is closer with that of NAPA. The average error of righting arm is 0.003 7 m, and the max error is 0.009 4 m. The accuracy and feasibility of the intact stability calculation based on 3D design data are verified.

ship intact stability; bulk carrier; loading computer; NAPA software

1000-8608(2017)05-0476-06

2016-12-23；

2017-07-17．

“八六三”国家高技术研究发展计划资助项目(2015AA016404)；海洋公益性行业科研专项经费资助项目(201505017-4)；中央高校基本科研业务费专项资金资助项目(3132016310).

王智洲(1993-)，男，硕士生，E-mail:wzzdmu@163.com；孙霄峰*(1978-)，男，博士，副教授，E-mail:xfsun_dlmu@163.com.

U661.22

A

10.7511/dllgxb201705006