关于圈龙图的奇优雅性
2017-09-20孙慧,姚兵*,2
孙 慧, 姚 兵*,2
( 1.西北师范大学 数学与统计学院, 甘肃 兰州 730070;2.兰州交通大学 电子与信息工程学院, 甘肃 兰州 730070 )
关于圈龙图的奇优雅性
孙 慧1, 姚 兵*1,2
( 1.西北师范大学 数学与统计学院, 甘肃 兰州 730070;2.兰州交通大学 电子与信息工程学院, 甘肃 兰州 730070 )
图的标号主要有 (奇) 优美标号、和谐标号、幸福标号、魔幻类标号等.圈龙图和多毛圈龙图可以作为计算机网络的模型.证明了圈龙图和多毛圈龙图都具有奇优雅标号,证明方法能够算法化,为网络模型的密码和可区别性研究提供了理论依据和可行的工具.
圈龙图;多毛圈龙图;奇优雅标号;叶子;奇优雅图
0 引 言
图标号研究起源于1967年Rosa的著名的优美树猜想[1].根据不同的条件,产生了各种类型的图标号,例如优美标号、奇优美标号、和谐标号、幸福标号、魔幻类标号等.图的标号在现代科学技术的诸多领域(计算机科学、信息科学、密码学、数学证明等)都得到了广泛应用.因此,图标号成为图论学科中发展迅速的分支之一[2-8].文献[8]收录了1 400多篇关于图标号的文章.而周向前[9]在2012年提出奇优雅标号的概念,给出若干构造奇优雅标号的方法,并给出一个猜想:所有的树都是奇优雅的.文献[9-13]是一些关于奇优雅标号的研究结果.Wang等在文献[14]中提出了“图结构+数论”的新型密码设计思想,目的是设计使用者方便、破译困难的图结构密码.这种设计需要足够多的图结构、图标号、灵活组合的策略.受文献[7,10]和环形计算机网络的启发,以及为Wang等的设计提供新的具有奇优雅性质的图结构,本文讨论与计算机网络有关联的圈龙图和多毛圈龙图网络模型.圈龙图是一种典型的环形计算机网络,每个顶点可以看作一个服务器;而多毛圈龙图是给圈龙图的任意顶点添加任意叶子得到的,一个叶子的顶点代表一个连接某一服务器的用户,多毛圈龙图是给圈龙图任意添加叶子的过程,它模拟了用户登录服务器的过程.文献[7]研究的模型也是一种环形计算机网络模型,但与本文研究的圈龙图略有不同,且文献[7]没有多毛圈龙图网络模型.
1 定 义
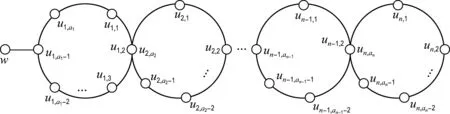
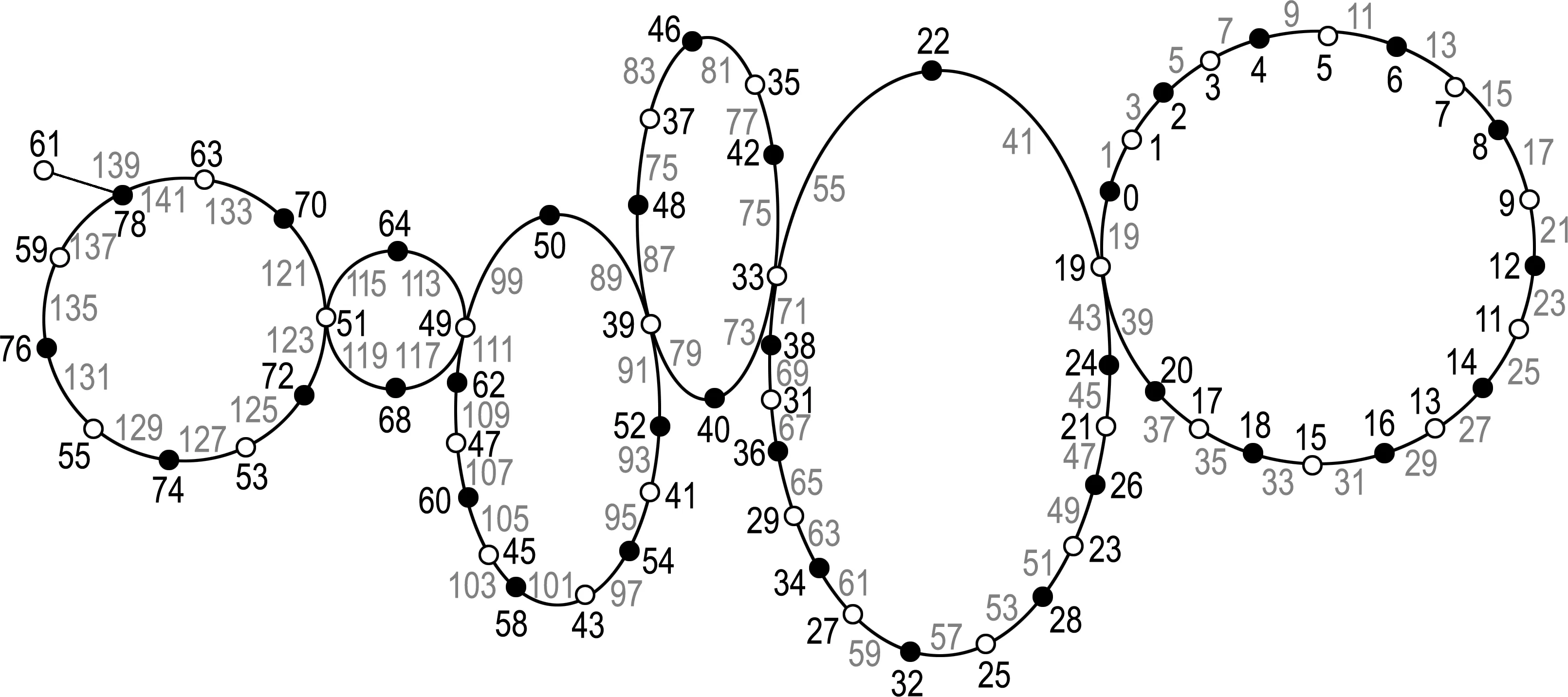
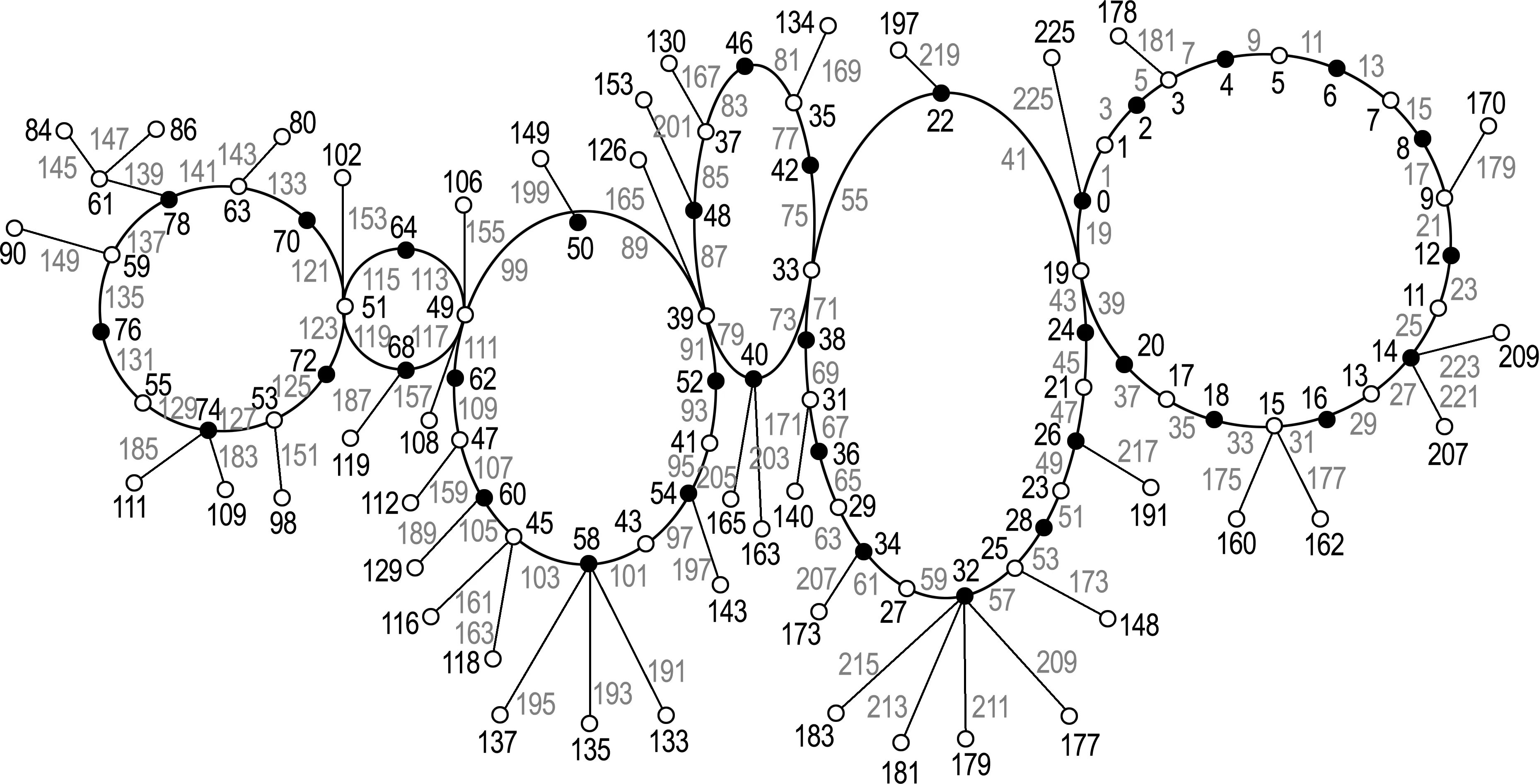
文中所考虑的图均为有限、无向、简单图.文中没有定义的术语和符号参见文献[15].为方便起见,用记号[m,n]表示集合{m,m+1,m+2,…,n},其中m和n均为非负整数,且满足0≤m 一个(p,q)-图G是指V(G)=p和E(G)=q.图G的一个从顶点集V(G)(或边集E(G),或全集V(G)∪E(G))到一个非负正数集的单射f是指任何2个不同顶点u、v(或2条边或2个元素)的像不同,即f(u)≠f(v),称f为G的一个标号(labelling).以下顶点标号集合{f(u)|u∈V(G)}简记为f(V(G)),边标号集合{f(uv)|uv∈E(G)}简记为f(E(G)). 定义1[8,16]对于给定的(p,q)-图G,如果存在一个单射f:V(G)→[0,q],使得边标号集合f(E(G))={f(uv)=f(u)-f(v)|uv∈E(G)}=[1,q],则称f是G的一个优美标号(graceful labelling),也称G为优美图(graceful graph).此外,若图G是具有顶点二部划分(X,Y)的二部图,且f满足max{f(x)|x∈X} 定义2对于给定的(p,q)-图G,如果存在一个单射f:V(G)→[0,2q-1],使得f(E(G))={f(uv)=f(u)-f(v)|uv∈E(G)}=[1,2q-1]o,则称G为奇优美图(odd-graceful graph),f是G的一个奇优美标号(odd-graceful labelling).若图G是具有顶点二部划分(X,Y)的二部图,且f满足f(X) 定义3[10]对于给定的(p,q)-图G,如果存在一个单射f:V(G)→[0,2q-1],使得f(V(G))=p和f(E(G))={f(uv)=[f(u)+f(v)](mod 2q)|uv∈E(G)}=[1,2q-1]o,则称G为奇优雅图(odd-elegant graph),f是G的一个奇优雅标号(odd-elegant labelling). 图1 圈龙图 证明设f是G的奇优雅标号.现定义X={v|f(v)是偶数,v∈f(v)},Y={v|f(v)是奇数,v∈f(v)}.显然,V(G)=X∪Y以及X∩Y=∅.因为G是奇优雅的,所以X和Y都是独立集. □ f(w)=F(1)-2n+3; f(u1,2k-1)=F(2)+2k+2n-4;k∈[1,α(1)] 当i∈[2,n]时 f(ui,2k)=F(i+1)+2k-2n+2i-1;k∈[1,α(i)] 另外,边标号集合f(E(G))={f(uv)=[f(u)+f(v)](mod 2q)|uv∈E(G)}. (1)先证明f(V(G))⊂[0,2q-1],以及对于任意的顶点u,v∈V(G),有f(u)≠f(v). 不难看出每个f(ui,2k-1)(i∈[1,n],k∈[1,α(i)])是偶数,每个f(ui,2k)(i∈[1,n],k∈[1,α(i)])和f(w)是奇数.令X={ui,2k-1|ui,2k-1∈V(G),i∈[1,n],k∈[1,α(i)]},Y={ui,2k|ui,2k∈V(G),i∈[1,n],k∈[1,α(i)]}∪{w}.注意到,当i∈[1,n]时,有f(ui,2k-1) 因此,f(V(G))⊂[0,2q-1],对于任意的顶点u,v,u≠v,有f(u)≠f(v). 因此,f(E(G))=[1,2q-1]o,对于任意的边uv,xy∈E(G),有f(uv)≠f(xy). 综合知:f满足奇优雅标号的定义,定理证明完毕. □ 图2是定理1的一个示例. 图2 解释定理1的一个例子 (i)令g(ui)=f(ui)(i∈[1,s]),g(vj)=f(vj)(j∈[1,t]). (ii)令g(u1u1,1)=2q′-1,g(u1,1)=g(u1u1,1)-g(u1)=2q′-1,其中g(u1)=0.定义多毛圈龙图G*的边标号为g(u1u1,j)=2q′+1-2j(j∈[1,l1]),其顶点标号为g(u1,j)=g(u1u1,j)-g(u1)=2q′+1-2j(j∈[1,l1]). 根据标号g的定义,有g(uiui,j)=[g(ui,j)+g(ui)](mod 2q′)=g(ui,j)+g(ui)(j∈[1,li],i∈[1,s]).g(vivi,j)=[g(vi,j)+g(vi)](mod 2q′)=g(vi,j)+g(vi)(j∈[1,ki],i∈[1,t]). 下面证明g是多毛圈龙图G*的奇优雅标号,叙述里省略“(mod 2q′)”. (1)下证g:V(G*)→[0,2q′-1].对于任意的顶点u,v∈V(G*),有g(u)≠g(v). 显然,每个g(ui)(i∈[1,s])是偶数,每个g(vj)(j∈[1,t])是奇数;每个g(ui,j)(j∈[1,li],i∈[1,s])是奇数,每个g(vl,r)(r∈[1,kl],l∈[1,t])是偶数.注意到0≤g(ui) 根据标号g的定义,有g(uiui,j)>g(uiui,j+1)≥2q+1(j∈[1,li-1],i∈[1,s]);g(uiui,li)>g(ui+1ui+1,1)≥2q+1(i∈[1,s-1]);2q+1≤g(vivi,j) 因为 g(usv1)=g(v1)+g(us)=2q-1, g(v1v1,1)=g(v1)+g(v1,1)=2q+1 以及 因此g(us,ls)>g(v1),g(v1,1)>g(us).故当u≠v(u,v∈V(G*))时,总有g(u)≠g(v),g(V(G*))⊂[0,2|E(G*)|-1]. (2)证明g(E(G*))=[1,2q′-1]o.多毛圈龙图G*的边标号由两部分组成:{g(uv)|uv∈E(G*)-E(G)}=[2q+1,2q′-1]o和{g(uv)|uv∈E(G)⊆E(G*)}=[1,2q-1]o,也就是说,g(E(G*))=[1,2E(G*)-1]o,满足奇优雅标号的定义,定理2得证. □ 解释定理2的一个例子在图3中给出。 图3 解释定理2的一个例子 本文探索了圈龙图和多毛圈龙图的奇优雅性.定理1证明了圈龙图具有奇优雅标号,定理2证明了多毛圈龙图也具有奇优雅标号.进一步研究发现多毛圈龙图完美地继承了圈龙图具有奇优雅标号的性质.需要注意的是,本文的圈龙图的圈Ci和Ci+1的连接点不能够任意,那么连接点任意的圈龙图的图是否也具有奇优雅标号呢?另外,多毛圈龙图是通过对圈龙图加叶子得来的,并且良好地继承了圈龙图具有奇优雅标号的性质,那么这种加叶子的方法是不是可以应用于所有的图,并且新图是否依然继承了原图的标号性质,这些都是今后需要继续研究的课题. [1] ROSA A. On certain valuation of the vertices of a graph [M] // ROSENSTIEHL P.TheoryofGraphs. New York: Gordon and Breach, 1967:349-355. [2] CHENG Hui, YAO Bing, CHEN Xiang′en,etal. On graceful generalized spiders and caterpillars [J].ArsCombinatoria, 2008,87:181-191. [3] KOTZIG A, ROSA A. Magic valuations of finite graphs [J].CanadianMathematicalBulletin, 1970,13:451-461. [4] 姚 明,姚 兵,赵振学. 关于太阳图魔幻标号的若干结果[J]. 甘肃科学学报, 2015,27(4):1-5. YAO Ming, YAO Bing, ZHAO Zhenxue. Some results on the magic labelling of sun-graphs [J].JournalofGansuSciences, 2015,27(4):1-5. (in Chinese) [5] 刘信生,刘元元,姚 兵,等. 龙图的优美性[J]. 兰州理工大学学报, 2013,39(3):133-135. LIU Xinsheng, LIU Yuanyuan, YAO Bing,etal. Gracefulness of dragon graphs [J].JournalofLanzhouUniversityofTechnology, 2013,39(3):133-135. (in Chinese) [6] 王宏宇,姚 兵,杨 超. 一类特殊对称图的边魔幻性 [J]. 四川师范大学学报(自然科学版), 2013,36(1):28-33. WANG Hongyu, YAO Bing, YANG Chao. The edge-magic property of a special class of edge-symmetric graphs [J].JournalofSichuanNormalUniversity(NaturalScience), 2013,36(1):28-33. (in Chinese) [7] FU Mingyan, LIU Xiaodong, WANG Ligong,etal. The graceful property of a kind of string graphs [J].JournalofSouthwestUniversityforNationalities(NaturalScienceEdition), 2005,31(6):843-851. [8] GALLIAN J A. A dynamic survey of graph labeling [J].TheElectronicJournalofCombinatorics, 2013,14:DS6. [9] 周向前. 关于图的优美、奇优美、奇优雅标号的研究[D]. 兰州:西北师范大学, 2012. ZHOU Xiangqian. The research on graceful, odd-graceful and odd-elegant labelings of graphs [D]. Lanzhou:Northwest Normal University, 2012. (in Chinese) [10] ZHOU Xiangqian, YAO Bing, CHEN Xiang′en. Every lobster is odd-elegant [J].InformationProcessingLetters, 2013,113(1/2):30-33. [11] YANG Sihua, YAO Bing, ZHANG Wanjia,etal. On odd-elegant properties of generalized sun-graphs [C] //2014IEEE7thJointInternationalInformationTechnologyandArtificialIntelligenceConference,ITAIC2014. Piscataway: IEEE, 2014:392-396. [12] XIE Jianmin, YAO Bing, ZHAO Tinggang. An algorithm and its implementation for odd-elegant labeling of general sun graphSm,n[J].JournalofShandongUniversity(NaturalScience), 2016,51(4):79-85. [13] XIE Jianmin, YAO Bing, HONG Wenmei. Odd-elegant labeling algorithm of generalized ring core networks [C] //20166thInternationalConferenceonMachinery,Materials,Environment,BiotechnologyandComputer(MMEBC2016). Amsterdam: Atlantis Press, 2016. [14] WANG Hongyu, XU Jin, YAO Bing. Exploring new cryptographical construction of complex network data [C] //2016IEEEFirstInternationalConferenceonDataScienceinCyberspace(DSC). Piscataway: IEEE, 2016:155-160. [15] BONDYJ A, MURTY U S R.GraphTheorywithApplications[M]. Amsterdam: North-Holland, 1976. [16] ZHOU Xiangqian, YAO Bing, CHEN Xiang′en,etal. A proof to the odd-gracefulness of all lobsters [J].ArsCombinatoria, 2012,103:13-18. Onodd-elegantqualityofcyclic-dragongraphs SUN Hui1, YAO Bing*1,2 ( 1.College of Mathematics and Statistics, Northwest Normal University, Lanzhou 730070, China; 2.School of Electronic and Information Engineering, Lanzhou Jiaotong University, Lanzhou 730070, China ) Graph labellings mainly include (odd-)graceful labellings, harmonious labellings, felicitous labellings, magic types of labellings. As known, (haired) cyclic-dragon graphs can be used to computer network models. The odd-elegant quality of (haired) cyclic-dragon graphs is proved, and the proof methods can be easily translated into algorithm. The work provides theoretical basis and feasible tools for cryptology and distinguishing research in networks. cyclic-dragon graphs; haired cyclic-dragon graphs; odd-elegant labelling; leaf; odd-elegant graph 2017-02-16; 2017-07-23. 国家自然科学基金资助项目(61163054,61363060,61662066). 孙 慧(1992-),女,硕士生,E-mail:18919104606@163.com;姚 兵*(1956-),男,教授,E-mail:yybb918@163.com. 1000-8608(2017)05-0531-06 O157.5 A 10.7511/dllgxb201705014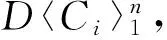
2 主要结论
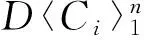
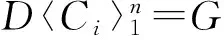
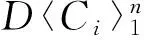
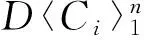
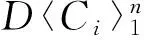
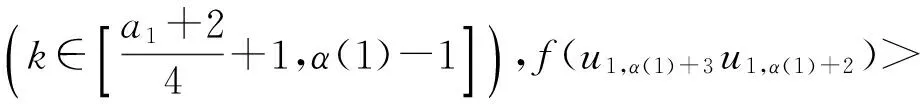
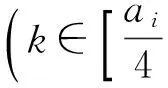
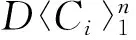
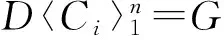
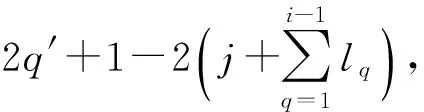
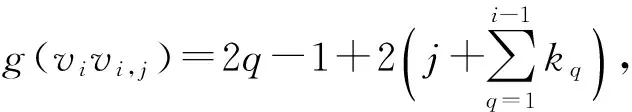
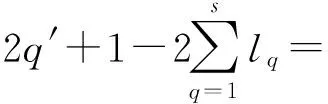
3 结 语
