房价非线性回归模型及期权定价

冯 敬 海， 朱 骏 桥

( 大连理工大学 数学科学学院, 辽宁 大连 116024 )

房价非线性回归模型及期权定价

冯 敬 海*， 朱 骏 桥

( 大连理工大学 数学科学学院, 辽宁 大连 116024 )

从宏微观经济学的角度出发，依照国家统计局网站的数据选取多个可能影响房地产价格的变量建立了全国房地产平均价格模型．运用R语言对数据进行了多元线性回归分析、多元非线性回归分析、相关性分析、多重共线性分析、岭回归分析等统计分析，得出房价的线性与非线性多个模型并进行了比较．结合随机微分方程、实物期权等相关金融数学知识进行了房价模型的理论推导与实际估计，并对房价期权进行了定价．利用Matlab对模型进行了大量的模拟并得到较好结果．

实物期权；房价模型；随机微分方程

0 引 言

房地产行业与我国经济发展始终相互影响，它的状况也间接反映了我国人民的生活水平．进入21世纪以来，我国经济全面发展，房地产作为我国经济的龙头行业发展速度越来越快．国家政策始终在一定程度上影响着房地产价格．1990年5月，《中华人民共和国城镇国有土地使用权出让和转让暂行条例》的出台，为土地使用权有偿出让提供了具体依据，为房地产市场形成和流转房地产的建立奠定了基础．2008年11月，4万亿元投资计划的实施抵挡了国际金融危机的冲击，阻止了GDP的下降，间接支撑了房地产行业的持续发展．诸如此类，数不胜数．近十年来，随着经济和教育水平的不断提高，房地产价格快速增长的原因成为国内各大高校学者热议的话题，与此相关的论文也层出不穷．影响房地产价格的因素较多，前人的论文所针对的方向各有不同，选取变量的依据大都为宏观或微观经济学原理加之一定的主观倾向，但依据的统计学方法如出一辙，得到的多元线性回归模型都可以很好地解释房地产价格的增长．

本文选取可能影响房地产价格的近10个变量进行统计学分析，数据来源于国家统计局网站．通过R语言[1]对多个变量与房地产平均销售价格进行相关性分析、逐步回归分析、非线性回归分析、岭估计等统计分析得到最优的拟合结果[2]．结合随机微分方程的相关知识对其进行深入的探索，利用Matlab对随机微分模型进行模拟，结合实物期权的相关知识对房价期权进行预测．

1 房价模型

1.1 房地产价格影响因素分析

经济学对人的消费理论有深度的研究[3]．影响我国房地产平均销售价格的主要因素有很多，本文选取了以下几个因素作为自变量：

x1：商品房年度销售面积，104m2；x2：广义货币M2，即交易货币以及定期存款与储蓄存款，亿元；x3：年末总人口，万人；x4：城镇人口，万人；x5：国民总收入，亿元；x6：国内生产总值，亿元；x7：人均国内生产总值，元；x8：城镇居民家庭人均可支配收入，元；x9：城镇居民家庭恩格尔系数，%

因变量y：全国商品房平均销售价格，元．

1.2 数据归一化

通过观察原始数据表可以发现，这些数据不仅单位有差异，并且数量级相差比较大．为优化这种数据的处理，需对各个自变量进行归一化处理．具体处理办法如下：

之所以采用这种归一化方法，是因为归一化后所有数据均处于0～1，消除了单位不一致的缺点．本文中归一化后的数据表示仍然采用归一化之前的符号．

1.3 多元线性模型的建立与求解

根据这9个变量建立y的多元线性回归模型：

y=β0+β1x1+β2x2+β3x3+β4x4+β5x5+β6x6+β7x7+β8x8+β9x9

首先，用R语言对数据进行拟合，step函数对其进行逐步回归，得到结果如表1所示(拟合后发现x9的P值最大，随后的拟合结果显示x8的P值最大，故将这两个变量剔除)．数据结果依然存在不够显著的情况，个别自变量与因变量之间正负相关关系不符合实际情况且可能存在多重共线性问题，故继续选择变量进行剔除，首先剔除不显著的x5．国内生产总值x6应该与房价y呈正相关，随后剔除变量x6，进而将不显著的x2剔除．得到结果如表2所示．

表1 线性回归模型数据初步拟合

表2 线性回归模型数据拟合

这已经是一个比较好的结果，但是x4的系数β4仍然为负．城镇居民人口越多，对房屋的需求量越大，导致房价变高．但是年末总人口x3的系数很大．考虑非城镇人口即乡村人口对y是否有影响，设x10=x3-x4，x10表示乡村人口总数(单位：万人)．拟合后得到结果：

y=-0.355 17+0.422 95x1+0.591 79x7- 0.739 56x9+2.631 38x10

该模型(模型1)与实际值对比如图1所示，将t与y的数据点、预测估计曲线、预测区间曲线和置信区间曲线画在一张图上，效果更加直观．

(a) 对比

(b) 区间

图1 模型1实际值与估计值对比

Fig.1 Comparison of actual and estimated values in Model 1

倘若不对变量x3和x4进行相减处理，由于x3和x4都是与人口相关的变量，数据中一定存在多重共线性．衡量数据是否存在多重共线性的一个重要指标就是矩阵XTX的条件数κ的大小，即

式中：X为数据标准化后的矩阵，λmin(XTX)和λmax(XTX)分别是矩阵XTX的最小特征值和最大特征值．条件数κ象征着XTX的特征值差异大小．利用R语言进行多重共线性分析得到矩阵XTX的最小特征值和最大特征值：λmin(XTX)=0.004 072 048 和λmax(XTX)=3.808 502，100<κ=935.281 088<1 000证明数据中存在中等程度的多重共线性．

采用岭估计的方法解决多重共线性的问题，对于多元线性模型y=Xβ+ε，岭估计的回归系数定义为β(k)=(XTX+kI)-1XTy，公式中k为大于0的可选择的参数，称之为岭参数．当k取不同值的时候，得到的估计结果也不同．若k=0，β(0)=(XTX)-1XTy即为普通的最小二乘估计．岭迹图如图2所示．

图2 岭迹图

岭回归的R语言函数还提供了两种确定岭参数的方法，计算后得出L-W=0.004 400 138和HKB=0.002 495 606，但这两种方法对于本问题得到的参数很不理想．所以，采用观测岭迹图的方法，当k>0.4时，各变量的岭迹趋于平稳，代入k=0.4后得到结果如表3所示．

表3 线性回归模型数据拟合(k=0.4)

其中x4的系数β4依然为负，但与其他变量系数相比较小，暂且得到模型2如下：

y=-0.338 23+0.228 29x1+2.141 08x3- 0.032 59x4+0.377 24x7

该模型与实际值的对比图如图3所示．

1.4 非线性模型的建立

通过观察数据发现，从1990年到2014年，大部分自变量及因变量y的值都显著增大，以变量x2为例，其在25 a间扩大了近100倍．不难看出，x2随着t的变化大致呈指数关系增长．假设它们之间的关系为x2=aebt，而后对等式两侧同时取对数，得到lnx2=lna+bt，对lnx2和t进行线性回归，计算出结果a=-353.7，b=0.175 3．指数函数x2=aebt与实际值的对比图4验证了本文的猜想．

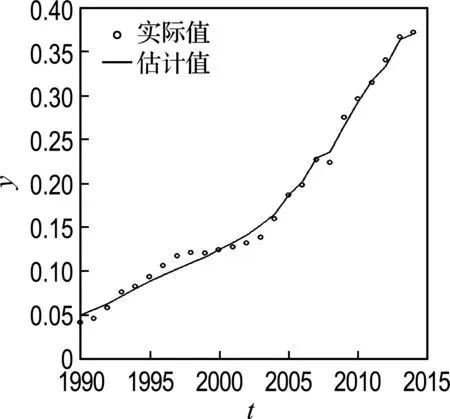
图3 模型2实际值与估计值对比

图4 x2=aebt与实际值

故假设房价与各变量之间的非线性模型为

lny=β0+β1lnx1+β2lnx2+β3lnx3+β4lnx4+β5lnx5+β6lnx6+β7lnx7+β8lnx8+β9lnx9+β10lnx10

由于变量x3、x4、x10均为与人口相关的变量，x6和x7均为与生产总值相关的变量，考虑多重共线性的问题，从这两组变量中各取一个变量并结合其他变量进行拟合．利用R语言中lm函数与step函数进行拟合和变量筛选，并从多种组合中选取最优解．于是得到模型的解：

lny=-0.490 56+0.238 95lnx1+ 0.871 15lnx2+0.713 15lnx9+ 1.634 10lnx10

恩格尔系数越高，说明人民生活相对艰苦，间接导致房价降低．尽管我国提出了计划生育等一系列控制人口增长速度的政策，我国总人口依然稳中有升，随着乡村人口的不断向城镇迁移，城镇人口逐年增加．而城镇房价显著高于乡村房价，故乡村人口应与全国房地产平均价格呈现负相关．故推测数据中仍然存在多重共线性的可能．100<κ=442.329 6<1 000表示数据中存在中等程度的多重共线性．图5为4个变量的岭迹图，选取k=1.7，各变量趋于平稳，得到多元非线性回归方程如下，即模型3：

lny=0.287 60+0.202 96lnx1+ 0.392 11lnx2-0.026 91lnx9- 1.005 66lnx10

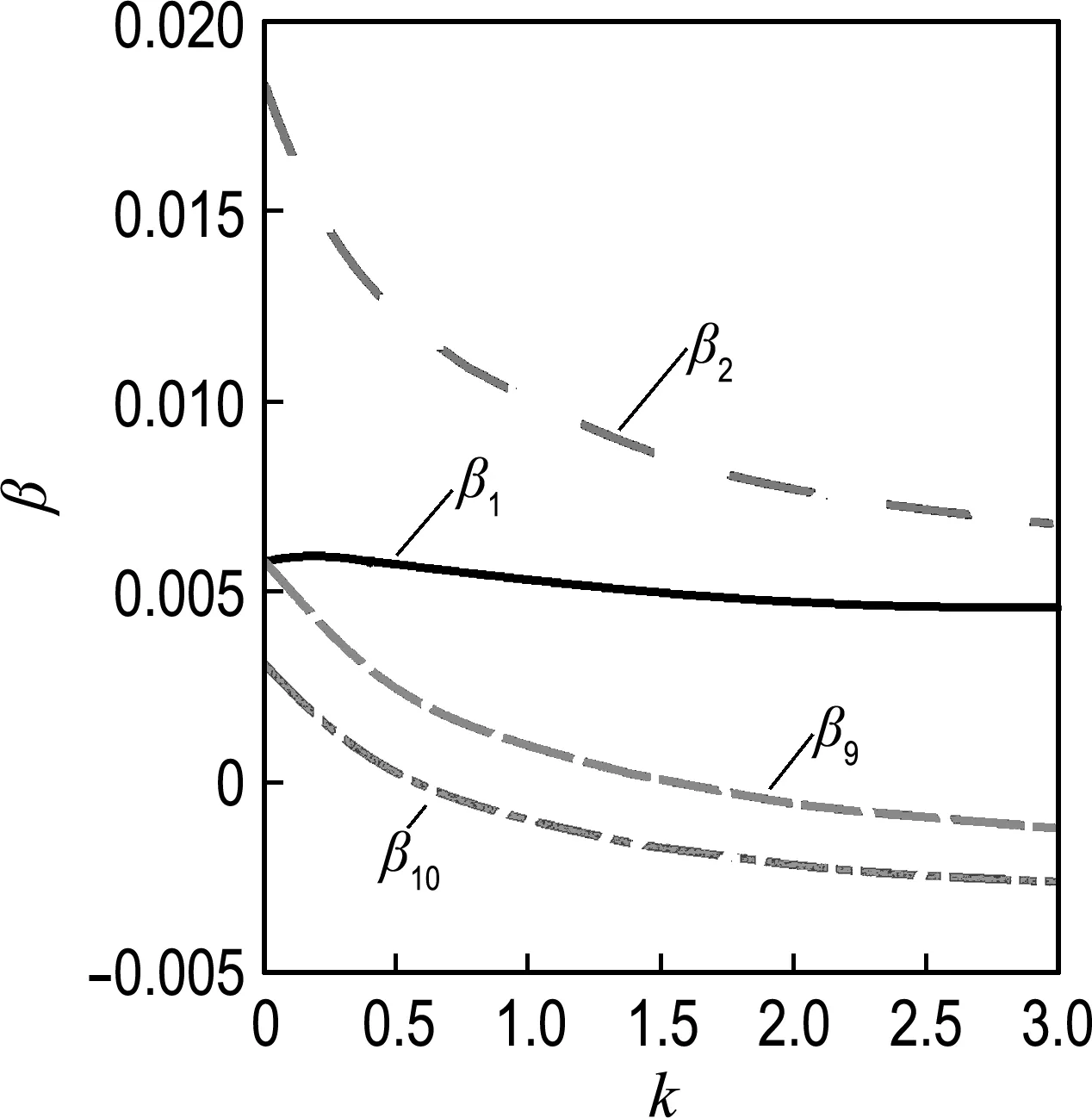
图5 4个变量的岭迹图

估计值与实际值之间的对比图如图6所示．

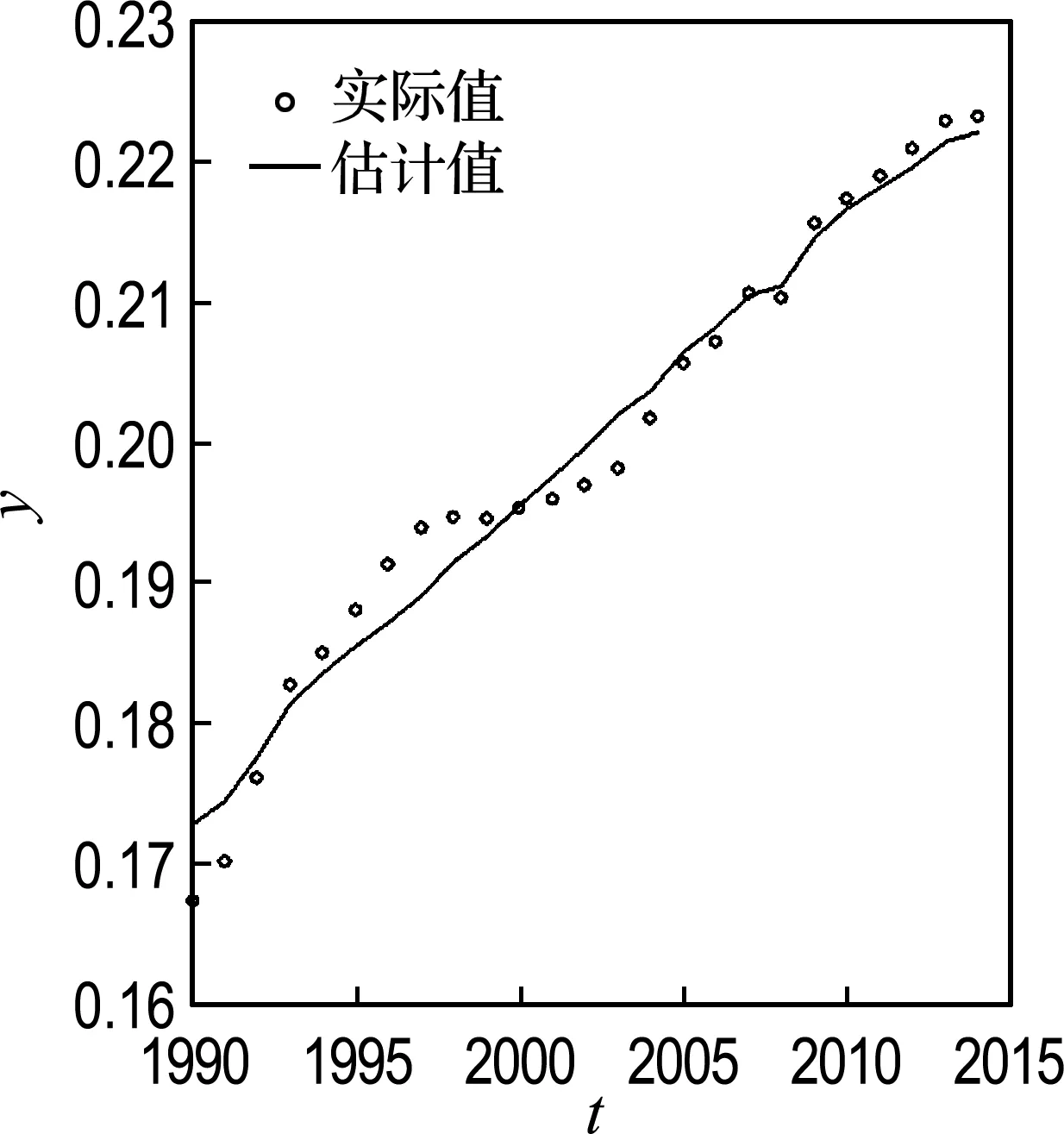
图6 模型3实际值与估计值对比

商品房年度销售面积x1与广义货币x2两个变量与全国商品房平均销售价格呈正相关．恩格尔系数x9、乡村人口x10与全国商品房平均销售价格呈负相关．其中，销售面积之所以逐年增长，是由于我国人民生活水平提高、对大面积住房的需求等多种因素所导致的．我国现阶段楼盘大户型越来越多，并且大部分地区户型越大房价越高．这说明市场需求量在增加，故销售面积的增加导致了房价的增加．人口的增长也会导致房地产需求的增加，房价的提高在预期之内．但城镇人口占全国人口比重较低，其生活水平却过高，对于房价的影响虽然显著，但却不符合常理．故选用更能接近全国平均消费水平的乡村人口作为变量研究，并且得到了很好的结果．

广义货币的增加，说明人们的购买力越来越强，增加了市场需求，从而引发了房价的上涨．随着生活水平的提高和时代的进步，人们的追求不仅限于房产，支配所拥有的财产的方式也越来越多．广义货币的变动也是国家货币政策的间接体现，从属于货币政策的利率政策、贷款政策以及公开市场业务都对广义货币x2有着显著的影响．该变量将国家政策间接、细致地体现于每一年的数据当中．模型中x2的系数β2较大也验证了国家政策对房价有着一定程度的影响．

由于模型1中x10与y呈正相关，模型2依然存在多重共线性，故选择模型3作为最终模型．

2 期权分析

2.1 模型及假设

根据上述模型得到：

假设Xi为几何布朗运动，dXi(t)=μiXi(t)dt+σiXi(t)dBi(t)，初值为Xi(0)，其中{Bi(t),t≥0}为布朗运动，μi>0,σi>0，i=1,2,3,4，(B1(t)B2(t)B3(t)B4(t))T为4维相关布朗运动，且当i≠j时，相关系数ρij=ρBi(t)Bj(t),ρii=1．Y(t)表示全国商品房平均销售价格,Xi表示影响Y(t)的变量．

命题1在引理1的假设下，Y(t)为几何布朗运动．

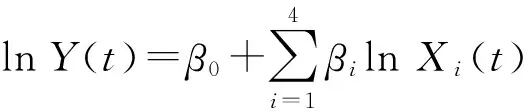
于是Y(t)=Y(0)eμt+σW(t)．

□

2.2 房地产价格的模拟

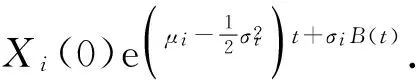
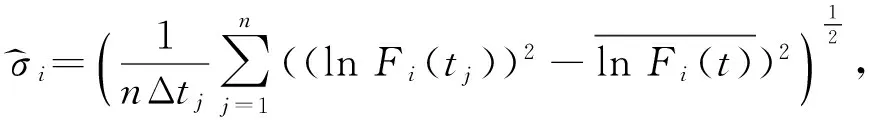
μ^i=1ΔtjlnFi(t)+12σ^2

其中

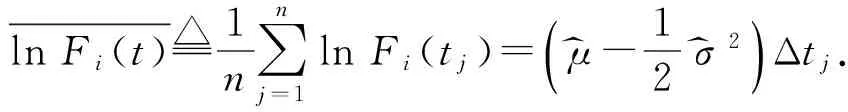
lnFi(t)1n∑nj=1lnFi(tj)=(μ^-12σ^2)Δtj.

代入归一化后的数据，n=24，Δtj=1，j=1,2,…,

最终计算得出μ=0.010 657，σ=0.006 993，得到关于Y(t)的随机微分方程：

dY(t)=0.010 657Y(t)dt+0.006 993Y(t)dB(t)

用Matlab软件模拟计算100 000次并取均值，发现模拟结果较好(图7)．其中1998年前后国际金融危机导致的房价增速缓慢轻微影响了拟合结果．

图7 随机微分模型的实际值与估计值对比

2.3 期权定价

设Y(0)为0时刻的房价，Y(t)为t时刻的房价，K为敲定价格，买入欧式看涨期权，收益(Y(t)-K)+，用C(t,Y(t))表示t时刻的期权[5]价值(t

首先考虑对冲思想，假设某人以全国房地产平均价格Y(t)购买了Δt处房产，并将剩余的资金存入银行，则得到如下资产组合：

dΠt=ΔtdY(t)+r(Xt-ΔtY(t))dt

根据本文假设及引理1的证明可知，全国房地产平均价格满足如下随机微分方程：

由期权定价基本定理[6]得

其中t∈[0,T]，Y(t)≥0．该方程即为Black-Scholes-Merton方程．假设该期权为欧式期权，则终值条件C(T,Y(t))=(Y(t)-K)+．Black-Scholes-Merton方程的解为

C(t,Y(t))=Y(t)N(d+(T-t,Y(t)))-Ke-r(T-t)N(d-(T-t,Y(t)))； 0≤t0

其中N是N(0,1)的分布函数，其中

3 结 语

本文所得的3个房地产价格模型各有各的特点，且拟合效果均达到预期效果，最终选取多元非线性模型作为最佳选择．对房价这一实物期权进行了预测，其意义在于不但增加了房地产交易的多样性，对房地产行业的持续发展有所帮助，并且为购买力较弱的居民提供了更大的选择空间．

[1] 薛 毅,陈立萍. R语言实用教程[M]. 北京:清华大学出版社, 2014.

XUE Yi, CHEN Liping.RLanguagePracticalTutorial[M]. Beijing: Tsinghua University Press, 2014. (in Chinese)

[2] 何晓群. 应用回归分析[M]. 北京:中国人民大学出版社, 2014.

HE Xiaoqun.AppliedRegressionAnalysis[M]. Beijing: China Renmin University Press, 2014. (in Chinese)

[3] 王 妍. 房地产供需及房价的数学模型研究[D]. 杭州:浙江大学, 2012.

WANG Yan. Supply and demand of real estate and mathematical model study of real estate price [D]. Hangzhou:Zhejiang University, 2012. (in Chinese)

[4] 张德丰. MATLAB数值分析与应用[M]. 北京:国防工业出版社, 2007.

ZHANG Defeng.MATLABNumericalAnalysisandApplication[M]. Beijing: National Defense Industry Press, 2007. (in Chinese)

[5] AMRAM M, KULATILAKA N.RealOptions:ManagingStrategicInvestmentinanUncertainWorld[M]. Boston: Harvard Business School Press, 2001.

[6] SHREVE S E.StochasticCalculusforFinanceⅡ [M]. New York: Springer-Verlag New York Inc., 2004.

Nonlinearregressionmodelandoptionanalysisofrealestateprice

FENG Jinghai*, ZHU Junqiao

( School of Mathematical Sciences, Dalian University of Technology, Dalian 116024, China )

Based on macro-micro economics, a national average real estate price model is established by selecting several variables which may affect real estate price according to the data of National Bureau of Statistics website. By using R language, multiple linear regression analysis, multiple nonlinear regression analysis, correlation analysis, multicollinearity analysis, ridge regression analysis are used, and a number of linear and nonlinear models are obtained and compared with each other. Combined with the stochastic differential equation and real option, and some relevant knowledge of financial mathematics, the theoretical deduction, practical estimate of real estate model and pricing of real estate price option are carried out. A lot of simulations are carried out by using Matlab to get a good result.

real option; real estate price model; stochastic differential equation

1000-8608(2017)05-0545-06

2017-01-08；

2017-07-20．

国家自然科学基金资助项目(11371077，11571058)；中央高校基本科研业务费专项资金资助项目(DUT15LK19).

冯敬海*(1970-)，男，教授，硕士生导师，E-mail:physics_7@163.com；朱骏桥(1992-)，男，硕士，E-mail:zjqqq1018@126.com.

O211.9

A

10.7511/dllgxb201705016