在说题教学中培养高中生的数学思维素养

念家桃（平潭县第一中学，福建平潭350400）

在说题教学中培养高中生的数学思维素养

念家桃
（平潭县第一中学，福建平潭350400）

在数学教学中，教师引导学生说题，可以让学生养成“说题、想题、做题、反思”的良好习惯。在说题教学中，可以通过说解法以培养学生的发散思维与独立思考能力，通过说变式以培养学生的创新意识与探索思维能力，通过说思想方法以提高学生的归纳总结能力与数学素养。

高中数学；数学说题；思维训练；有效学习

学生的数学学习活动不只限于接受、记忆、模仿和练习，在数学教学过程中，教师应倡导自主探索、动手实践、合作交流、阅读自学等多样化的数学学习方式。“说题”是一种促进教师专业发展的教学教研活动，也是一种促进学生思维发展的学习途径，在数学教学中，教师引导学生说题，可以让学生养成“说题、想题、做题、反思”的良好习惯。

说题包括学生说题和教师说题。教师说题，类似于说课，是一种教育教研和讨论活动，也是一种深层次备课后的展示与一种教学方式。学生说题，是一种旨在深化学生解题思维习惯与思维品质的学习活动，在提高学生问题解决能力的同时，有助于培养学生的发散思维，激发学生独立思考的能力，有助于培养学生的创新意识，发展学生勇于探索的能力，有助于培养学生的归纳总结能力，提升学生的数学素养。

高中数学说题的内容大致包含：说解法、说变式、说思想方法、说背景、说规律、说反思、说错解等等。笔者结合多年来的教学经验在课堂上开展说题活动，从教师“说”到学生“说”，课堂上气氛热烈，学生的学习成绩显著进步。

一、说解法以培养学生的发散思维与独立思考能力

波利亚说:“问题是数学的心脏，掌握数学意味着什么？那就是善于解题。”从不同的角度去思考问题，从不同的方向去寻找解题策略是学生要掌握的能力。为此，教师可选择在说题的教学活动中培养学生的发散思维，以及学生的独立思考能力和创新意识。

在课堂上，教师与学生可以先围绕问题的解法展开说题活动：

解法3.两边平方去根号并整理得：y2=4+把两个根号问题转化为一个根号的问题，再利用二次函数求出最大值。

解法4.利用导数工具研究函数的单调性，令f′(x)=0得：x=-1，所以函数f(x)在(-3，-1)上单调递增，在(-1，1)上单调递减进一步求出函数的最大值，体现了通性通法。

我们在解题教学过程中，不能盲目追求数量不顾质量，陷于题海战术，而应着力教会学生思考，对一个问题的多思路分析，能让学生的思维产生迁移与发散，从而提高学生思维的敏捷性和灵活性，以及分析与解决问题的能力。

二、说变式以培养学生的创新意识与探索思维能力

高中学生的思维十分活跃，在说题教学中，教师有意识地引导学生对问题进行引申与拓展，有助于培养学生的创新意识，发展学生勇于探索的思维能力。例如，在求函数f(x)=最大值的问题中，我们可引申出以下变式题：

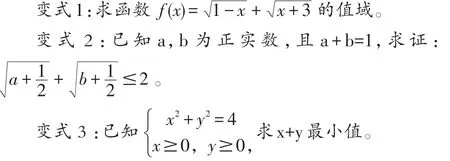
教材中的例习题都经过精心设计和严加挑选，在教学中，教师要充分利用这些例习题进行引申与拓展，通过一题多变，一题多用，一题多解和多题一解等方式，提高学生灵活运用知识的能力。高中数学题的变式教学要做到循序渐进、有的放矢，要紧密联系以前所学知识，在新知识的学习中复习巩固旧知识，以提高学习效率。习题的变式教学可以培养学生的发散思维，提高他们解决实际问题的能力，有时候，这种变式教学甚至可以跨学科进行，比如，可以用甲烷的分子结构图对正四面体问题进行变式。习题的变式教学要紧扣考试说明不要编造繁、难、杂、怪类问题，以免浪费学生的学习时间，挫伤学生的积极性。

引申与拓展和真正意义上的反思与创新有很大的距离，但是它可以使学生明白，一个问题解完了并非结束了，如果能够做出一些有益的变式拓展，对理解和掌握数学知识和解题策略，都有事半功倍的作用，对发展学生勇于探索的思维能力有很大作用。

三、说思想方法以提高学生的归纳总结能力与数学思维素养

学数学需要解题，但解题不是数学学习的全部内容，领悟数学思想掌握数学方法才是数学学习的精髓，离开这一点，解题将是低效甚至是无意义的。

数学思想方法是从数学知识中凝炼出来，是将数学知识转化为数学能力的桥梁。在上述例题五种解法及其变式解法中，教师要引导学生总结出其中用到的“转化（化归）思想、数形结合思想、函数与方程思想”等数学思想，以提高学生对数学的认识与理解水平。

在2009年福建高考理科试卷中，有一道这样的填空题：若曲线f(x)=ax3+1n x存在垂直于y轴的切线，则实数a的取值范围是______。由于问题中的曲线f(x)=ax3+1n x存在垂直于y轴的切线，故有f′(x)=0，即3ax2+=0有大于0的解，这里蕴含了化归与转化思想。我们可以将3ax2+=0化为3ax3+1=0，讨论a＞0，a=0，与a＜0三种情形，只有当a＜0时，方程有正数解，这里蕴含了分类与整合的思想，以及方程的思想；将3ax2+=0化为3a=，因为x＞0，所以a＞0，这里蕴含了函数的思想与变量分离的思想；将3ax2+=0化为3ax2=，在同一直角坐标系内画出y=-与分别当a＞0，a=0与a＜0时y=3ax2的图象，发现只有当a＜0时两图象有交点，且交点的横坐标大于0，这里蕴含了数形结合的思想，分类整合的思想。

“授之以鱼，不如授之以渔”，方法的掌握，思想的形成才能使学生终身受益。用数学思想指导解题思维，可最大程度地培养思维的发散性、灵活性，能对问题灵活变通与引申拓展，提高数学思维的深刻性。

通过一年的“学生说题”课题实验教学研究，从刚开始引导学生按波利亚的“如何解题表”提供的方法去“说题”，到后期学生能围绕数学题目进行“说题”，遇到比较难的数学题目时，也可以说说做不出来的原因或碰到的困难，说出自己的想法，或者对问题的结论进行猜想。通过与非实验班的对比，参与“学生说题”的学生学习更积极主动，同学间交流更多了，同学们也喜欢将自己对数学问题的理解或解法与其他同学分享，这也说明“学生说题”的教学实践是成功的。

说题提供了一种很好的研修模式，对学生学习数学有较大的促进作用。它可使学生学习的自主意识有明显提高；学生自主学习能力有明显提高；学生的数学成绩有明显提高。在教学中充分挖掘例题的潜在功能，通过对例题的巧妙变式及一题多解和一题多变训练，可以培养学生多角度、多层次地去思考和解决问题，培养学生的思维能力，提高解题能力。对数学问题能够执著探求，对数学新问题能够不断学习、反复思考、解题方法及时调整、寻求更优解法，将会使他们的数学成绩有质的飞跃。

［1］张晓东.说题与数学青年教师的专业成长[J].中学数学教学参考，2015（3）.

［2］徐敏亚.数学课堂让学生经历真学习[J].中学数学教学参考，2015（3）.

［3］江忠东.小试题中的大信息[J].中学数学教学参考，2015（4）.

（责任编辑：王钦敏）