基于翻转课堂的高中数学导学案设计与思考

陈言（福州格致中学，福建福州350001）

基于翻转课堂的高中数学导学案设计与思考

陈言
（福州格致中学，福建福州350001）

翻转课堂教学模式颠转了知识传授和知识内化的过程，基于翻转课堂的高中数学导学案可以为学生的学习搭建平台、提供“脚手架”，利用导学案中“导”的功能和“学”的任务可以为学生的自主学习、主动学习提供帮助，实现课前、课中、课后的有效学习。

翻转课堂；导学案；设计与思考

一、引言

翻转课堂教学模式是信息时代在学习方式和教育模式上的一次创新，其特点是翻转传统的教学流程，将“课堂讲解—课后作业”变为“课前学习—课堂研究—课后拓展”的教学过程，其核心思想是“先学后教、以学定教”。在翻转课堂里，学生掌握着学习的主动权，是知识的主动建构者，但由于学生直接面对新内容、新问题、新情境，这可能会给他们的学习带来一定的困难，解决这一问题的有效抓手就是根据学生的实际情况合理设计导学案，为学生提供学习的支架、路线图，提供自主学习与思考探究的问题情景，让每位学生都能在最近发展区内自主探究、主动思考、获取知识、发展能力。所谓导学案“是指教师通过对课标、教材、学情的深入研究，依据学生的认知水平、知识经验而编制的用于指导学生主动参与、合作探究的学习方案”。［1］目前，导学案在打造高效课堂方面以其特有的实效性受到广大教师的关注，本文以“等比数列的前n项和”为例，介绍基于翻转课堂的导学案设计，探究如何设计使用导学案。

二、课前学习导学案

课前学习（前置学习）环节是学生获取知识的环节，学生利用学习资料和微视频学习，对新知识产生一个基本的认识，作为学习活动的组织者，教师应认真研究教材和课程标准，明确学生应达到的目标，合理安排前置学习的内容，合理设计导学案，笔者对等比数列前n项和的前置学习导学案设计如下：

1.学习目标

（1）通过类比、归纳，猜想，写出等比数列的前n项和公式。

（2）运用特殊与一般、分类与讨论、化归与转化等数学思想，推导等比数列的前n项和公式。

设计说明：为了给学生指明学习方向和达成目标，教师尽可能使用“写出”“运用”等有明确指向的词语，使学习目标的表述具体、清晰。

2.学习重点和难点

重点：等比数列的前n项和公式的推导。

难点：分析等比数列的结构特点推导等比数列的前n项和公式。

3.学习过程

【知识回顾，提出问题】

在学习等差数列时，我们研究过等差数列的前n项和，其探究的方法是从高斯算法中获得启示，利用倒序求和的方法得到，对于等比数列怎样求其前n项和？

设计意图：以类比的方式直截了当地提出问题，让学生明确要学什么并思考怎么学。

【探索分析，猜想论证】

（2）能类比等差数列求和公式的推导方式求Sn吗？上式中每一个括号里的和是否都相等？

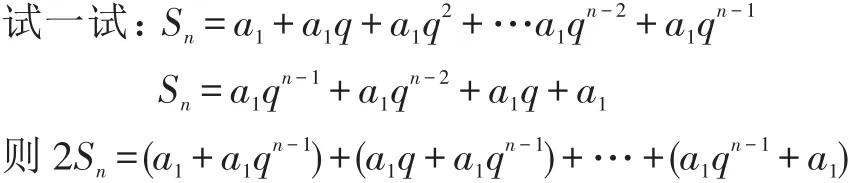
设计意图：选择与等差数列求和公式的推导进行类比作为“引思”“设疑”的点，让学生思而生疑，以疑促思。

（3）用倒序求和的方法行不通，需要另辟蹊径，我们从特殊化入手去发现规律，猜想结论。

若q=1则Sn=na1，若q≠1，当n=2时,S2=a1+a2= a1+a1q=a1(1+q)，当n=3时,

S3=a1+a2+a3=a1(1+q+q2)，……，依次类推请写出Sn的表达Sn=a1+a2+…+an=a1（）。

上面的式子较长，能化简吗？

设计意图：对等比数列前n项和公式的探索，导学案设计的重点放在如何调动学生的积极性，如何指导学生开展学习上，为了发挥导学案“导”的功能，笔者设计使用“归纳-猜想-演绎”的学习方式取代课本纯演绎的学习方式，以知识的再发现过程和学生思维的发展过程为主线，学生通过体验、感受，自主完成等比数列前n项和公式的推导。

【思考题】等比数列前n项和公式还有其它的推导方法吗？

三、课堂探究导学案

针对课堂探究活动，导学案的编制应突出学生的主体意识和问题意识，可以将要求学生掌握的知识和方法设计成一个个问题，用问题来引导和促进学生学习，用问题来拓展和深化学生思维，导学案的设计就是要使学生学习有“路”，学习有“法”，成为学生课堂学习实践过程中的学习方案和操作方案。

1.课堂交流、合作探究

课本上等比数列前n项和公式的推导方法我们称之为“错位相减法”，其它推导方法的研究如下：

你还有其它的推导方法吗？请写出来与大家交流。

设计意图：方法一源自2000多年前古埃及人的递推方法，方法二源自欧几里得比例法，课堂探究活动不应拘泥于教材上的一种方法，应鼓励学生通过积极思考，从不同的角度对公式进行推导与证明，拓展学生的数学思维。

2.构造模型，数学实验

对于正数等比数列{an}，首项为a1，公比为q求其前n项和的实验：

有了以上发现，我们是不是又得到了等比数列前n项求和的一种推导方法？请写出来。

设计意图：发挥导学案“学做”的功能，引导学生开展数学实验。

3.学以致用，解决问题

例1求下列等比数列的前8项和

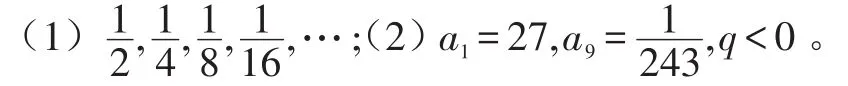
设计意图：有了等比数列的通项公式和前n项和公式，如果已知Sn.an,q,a1,n五个量中的任意三个，就可以求出其余的两个，本例是对等比数列的前n项和公式的直接应用，同时渗透了方程思想。

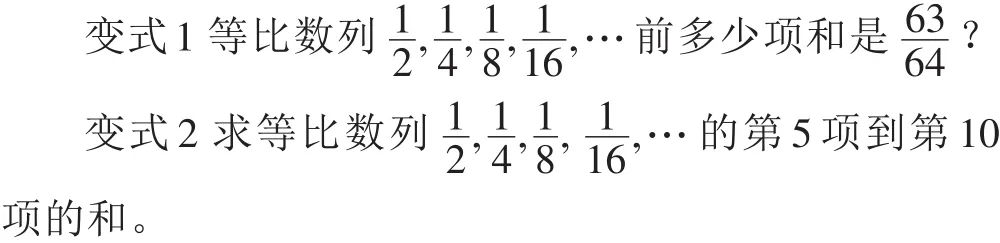
方法1：观察、发现：a5+a6+…+a10=S10-S4。

方法2：此等比数列的连续项从第5项到第10项构成一个新的等比数列：首项为，公比为q=，项数为n=6的等比数列，所求和为_____。

分析：数列中的第n项c=n是由a=n和b=1n2nnn2n相乘而来，由于每一项中的n不一样，所以不能直接运用等比数列求和公式。如何将不可求和的式子转化为可求和的式子?如果能够把数列的前n项和化为，就可以用等比数列求和公式计算，如何把“系数”化为相同呢？可以用“错位相减法”吗？请写出过程。

变式4求和：Sn＝1＋3x＋5x2＋7x3＋…＋(2n－1)xn-1(x≠0)。

分析：当x=1时，Sn=？

当x≠1时，可以用“错位相减法”求Sn吗？

设计意图：应用环节的重点是方法的使用以及问题的解决，是基于学生的角度设计问题，通过一题多解及一题多变，提炼数学方法，感悟数学思想，形成解题技能，优化思维品质，提高思维水平。

四、课后学习导学案

课后学习导学案内容包含对本节课所学知识和方法的小结、课后作业、延伸探究等，采用任务驱动的方式，引导学生及时复习，整理归纳。推荐的作业应当数量合适，难度适中，可以适当设置选做题，满足不同层次学生的需要，并要求学生按时完成推荐的作业。

1.学习体会：本节课一方面是“等差数列的前n项和”与“等比数列”内容的延续，另一方面它又为进一步学习等比数列前n项和性质等内容做准备，就知识的应用价值上来看，它是从数学问题和现实问题中抽象出来的一个模型，公式推出中所蕴含的数学思想方法有着广泛的应用，请总结本节课所用到的数学思想方法。

2.推荐作业：课本P61A组2、3、4、5，选做：课本P62B组1。

3.查阅与研究：（1）“芝诺悖论”，并从数列求和的角度加以解释；（2）中国古代数学文献《九章算术》衰分章第二题及第四题。

五、思考与感悟

1.导学案设计的理论基础

根据布卢姆的掌握学习理论，教师要为学生的掌握而教学，学生要为自己的掌握而学习。教师能够帮助每一位学生很好地学习，但每一位学生掌握同样的教学内容所需要花费的时间是不一样的，因此教师需要思考如何提高教学质量，为学生个性化的学习提供帮助。按照维果斯基“搭建脚手架”的理念，教师应根据学生的“最近发展区”把复杂的学习任务加以分解，一方面要为学生提供促进其发展的学习任务，另一方面还要为学生搭建完成这些学习任务的“脚手架”。基于翻转课堂的高中数学导学案可以为学生的学习搭建平台、提供“脚手架”，实现课前、课中、课后的学习，学生可以利用导学案中“导”的功能，依据导学案中“学”的任务，明确自主学习的内容、目标和方法，开展“自主探索、动手实践、合作交流、阅读自学”活动，因此，导学案是学生学习的“路线图”“指南针”“方向盘”，“是学生学习的起点，也是将要到达的目的地”，［2］导学案的设计和应用既符合维果斯基的“搭建脚手架”理念以及布卢姆的掌握学习理论，也符合《普通高中数学课程标准（2003实验版）》所倡导的“积极主动，勇于探索”的学习方式和要求。

2.导学案设计的问题情境

问题在导学案中“既是教师‘导’的基本思想策略和方法的体现，又是学生‘学’的过程体现”［2］，问题的设计不仅要具有科学性、针对性、实效性和启发性，而且要能够有效化解学习难点。比如人教A高中数学必修5的教材是运用“错位相减法”对等比数列前n项和公式进行推导，学生理解起来可能一时会有困难，针对这一情况，在导学案问题的设计上可以运用类比联想、由特殊到一般等方法引导学生开展“归纳-猜想-演绎”的学习活动，学生通过观察、分析、归纳、猜想、论证等思维活动，在对问题的思考过程中主动建构知识，在解决问题的同时既掌握了方法，又提高了能力。对问题的设计不仅要考虑如何化解学习难点，还要考虑如何“学”，考虑学生如何在问题的驱动下产生认知冲突并在已有认知结构的基础上探究新知。

3.导学案设计的层次性

翻转课堂以课前学生自主学习，课堂学生自主、合作探究，是翻转课堂教学的主要模式，这一模式的核心理念有两个：一是发挥学生在学习过程中的自主性和积极性，“让每个学生按照自己的步骤学习”；二是互动的个性化指导。因此，基于翻转课堂的导学案设计不仅应有利于学生实现对知识和方法的掌握，而且还应该让每位学生都能得到发展。从学生的差异性方面考虑，导学案的设计应有利于因材施教，做到对学困生有帮助、对中等生有启发、对尖子生有挑战。导学案的设计还包括对一节课的总体设计，需要设计者认真研究教学内容，把握好每节课的目标、要求，设计的学习活动应由易到难、由浅入深、由表及里、螺旋上升、逐步提高。

［1］王俊亮.导学案在高中数学命题教学中的应用研究［D］.济南：山东师范大学，2011.

［2］黄发国，张福涛.翻转课堂导学案编写指导与案例分析［M］.济南：山东友谊出版社，2014.

（责任编辑：王钦敏）