畅你所见——埃舍尔艺术作品的数学美

安徽省合肥师范学院数学与统计学院 阮 征

畅你所见
——埃舍尔艺术作品的数学美

安徽省合肥师范学院数学与统计学院 阮 征

埃舍尔是将理性思维和艺术表现发挥到极致的艺术家和思想家。在他的艺术作品中，往往能够体现数学思维融入绘画艺术创作，为绘画艺术增添了数学之美，其作品被科学家认可。如果说数学家开启了通往宇宙之门的钥匙，那么埃舍尔就是那个将理性思维和艺术表现发挥到极致、把情感和生灵给予这个空旷的世界的艺术家。他的作品的成功之处不仅来源于他精湛的绘画能力，而且在于他将数学美融入艺术创造中。本文通过介绍数学美的内容和最数学的画家埃舍尔，从平面镶嵌、多面体、空间形状、拓扑学效果和自我复制五个方面走进埃舍尔的“不可能”世界，剖析埃舍尔艺术作品中所能看见的数学美，领略埃舍尔赋予这些抽象的数学美以具体的表象。

埃舍尔；数学思维；数学美

爱美之心，人皆有之。人们执着地追求美，但什么是美，却很少有人能够具体地描述出来，当我们看到一幅精美的图画时，便会感到心情愉悦，受到一种美的熏陶，这难道不就是一种美吗？现如今，数学已渗透到文学、音乐、美术、建筑等大量领域之中，之所以数学可以如此广泛地存在于生活的各个方面，就在于数学存在一种美，数学美是丰富的，如数学结构系统的协调性、对称性，数学命题与数学模型的概括性、典型性与普遍性，数学中的奇异性等都是数学美的具体内容。20世纪最伟大的数学家希尔伯特把数学比喻为“一座鲜花盛开的园林”，由此足以看到艺术与数学美有着悠远的历史。早在公元前6世纪，毕达哥拉斯就把数与美联系起来，将数看作是美的本源，认为“事物由于数而显得美”，一切艺术都产生于数，甚至整个天空都是一个音乐的音阶和一个数。数学家和物理学家用数字符号描述这个世界，而在荷兰图形艺术家摩里茨·科奈里斯·埃舍尔看来，“在数学领域，平面规则分割已经从理论上获得了充分的研究，数学家打开了一扇通向无限可能性的大门，但是他们自身并没有进入其中看看，他们特殊的禀赋使他们对如何打开这扇门的方式更感兴趣，而对隐藏在其后的花园不感兴趣。如果我们想构建一个宇宙，不能让它是模糊不清的抽象物，而必须是可以识别的具体形象”。埃舍尔的创作笔记《不规则图案的平面规则分割》等，证明了他和达·芬奇一样，都是致力于对艺术创作的基本原理做彻底探究的艺术家。下面就走进埃舍尔艺术作品中的“不可能”世界，去领略其中的数学美。

一、最数学的画家埃舍尔简介

1898年出生在荷兰的埃舍尔，自称是一个“图形艺术家”，专门从事木版画和平板画。1956年，埃舍尔举办了生平第一次重要的画展，这个画展得到了《时代》杂志的好评，使他获得了世界范围的名望，许多数学家给予了埃舍尔艺术作品充分的肯定，认为埃舍尔的艺术作品中数学的原则和思想得到了非同寻常的形象化。后来随着埃舍尔创作的发展，创造了许多反映悖论和“不可能”的图形结构的艺术作品，让全世界看到了艺术作品中的数学美。

二、剖析埃舍尔艺术作品中的数学美

1．镶嵌图形

我们都知道，规则的平面分割叫作“镶嵌”，镶嵌图形是完全没有重叠并且没有空隙的封闭图形的排列。一般情况下，构成一个镶嵌的封闭图形的基本单元是多边形或类似的常规形状，然而更使埃舍尔着迷的是那些不规则的、形状特别的平面镶嵌。埃舍尔曾经在他的一篇关于镶嵌图形的文章里谈到：“从数学领域来看，规则的平面分割已经在理论上进行了研究……难道这意味着它只是一个严格的数学问题吗？按照我的意见，它不是。数学家打开了一扇通向无限可能性的大门，但是他们自身并没有进入其中看看。他们特殊的禀赋使他们更感兴趣的是如何打开这扇门，而不是门后面的花园。”

埃舍尔平面镶嵌的很多艺术作品中，都运用了几何学中的反射、旋转来得到更多变化的图案，埃舍尔也努力使这些图案通过扭曲变形成为人、鸟、鱼、蜥蜴等动物，这样的效果既是美不胜收的，又是令人拍案叫绝的。当中体现出最为神奇的数学美是埃舍尔的平面镶嵌图形每次都能铺满整个平面，下面以埃舍尔的《黑白鸟的镶嵌》（如图1所示）和《骑士平面镶嵌》（如图2所示）为例：

图1

著名数学家彭罗斯多次提到埃舍尔的设计思路对数学思维的启发，在黑白鸟的平面镶嵌里，观众看到的是向西北方向飞翔的深色鸟和白色鸟布满了整个平面，通过镶嵌图形形成的黑白鸟在变化中并不脱离最初的图案。现在经常将这些图案模式运用到多边形的镶嵌图形中。

图2

而《骑士平面镶嵌》就给观众呈现了某种怪异的对称现象，假如把白骑士看作一个图形，黑骑士就成了“背景”，倘若把黑骑士揭起来，翻转180°，就可以和原来的白骑士重叠，不仅表现出了数学上翻转、重叠的美，也表现了物理世界中某种“对称”的破坏和缺损——在弱相互作用下的“守称不守恒”，可见艺术不仅和数学有密切联系，也和物理、科学之间有着相通之处。

2．多面体

对埃舍尔来说，数学上规则的几何体中，多面体尤为具有特殊的魅力，他把多面体作为自己许多艺术作品的第二重要元素出现。

从理论上讲，正四面体、正方体、正八面体、正十二面体和正二十面体这五种立体图形可以被视为理想的多面体，即有4个三角形表面的正四面体、有6个正方形表面的正方体、有8个三角形表面的正八面体、有12个五边形表面的正十二面体，在他的木版画作品《四个常规的几何体》中，将四种多面体匀称地交叉，使它们呈现出半透明状，观众可以有效地辨认出来。

图3

交叉几何体常出现在埃舍尔的艺术作品中，体现出浓厚的数学美，以这幅有趣的木版画《星空》（如图3所示）为例：这是一个由八面体、四面体、立方体和变色龙交叉构成的几何体，这些正面体都是外凸的，同时还存在内凸的正多面体，数学家已证明出存在26种可能的规则立体，它们之间互相交叉还可以形成无数规则的立体系列，然而倘若单单画出这些规则的立体几何，想让观众对这幅艺术作品产生兴趣是十分困难的，可在这里，埃舍尔引入了两条栩栩如生的变色龙，使它们居住在这个周围一片漆黑且飘浮着无数规则立体星空的奇妙正多面体中，带给观众一种奇妙的视觉冲击，完美展现出了立体几何的数学美。

3．空间的形状

在埃舍尔用数学观点完成的所有重要艺术作品中，最重要的是处理空间性质的作品，以《瀑布》（如图4所示）为例，从中可以看到很多美妙的几何图形，更容易会发现原来富有规则的线条也是那么令人着迷。不禁引发观众思考：是否存在这样一种图形（如图5所示）？

图4

图5

这种图形在数学上被称为彭罗斯三角，是所有不可能图形中最基础、最著名的一个。彭罗斯三角被很多人独立发现过，最早的也许是1934年18岁的瑞典学生奥斯卡·路特斯瓦德的课堂涂鸦。在看到了埃舍尔的作品《楼梯房间》（如图6所示）之后，罗杰·彭罗斯和他的父亲一起写了一篇论文，分析了这种错觉以及当中存在的数学美，从而提炼出彭罗斯三角和彭罗斯楼梯等几个基本形态，还把这篇论文寄给了埃舍尔，反过来埃舍尔受此启发，创作出了最有名的不可能作品《瀑布》。

图6

反观《瀑布》，不难发现这个瀑布本质上就是两个彭罗斯三角的叠加，形成了矛盾的空间，显示了埃舍尔对空间维度的关注以及用二维的方式表现三维空间的矛盾和诡术，刚性的维度在埃舍尔手中好像成了一团面，可以任意扭转弹拉、可以在自己想象空间里展现出各种不同维度空间和它们不可思议的魔法转变。

以下面这幅《三个球面》（如图7所示）为例，这三个简单的几何体号称球面。对于最上面的几何体，观众都毫不犹豫地认为这是个球面，可万万没想到这只不过是一个在二维平面上画的球面。埃舍尔把这个球面折了一下，经纬线做了一定的变动，将其放到了中间，观众眼里就看到了一个半球面，仍然没料到这个半球也在二维平面上。继续压那个球面，直至它成了一张皮，摊在桌上，观众这才意识到最下面的那个是一个二维的圆，可这个二维圆却在一个三维空间里，更像是三维球面在一个三维桌的桌面上的投影。

图7

从这些空间形状的艺术作品中我们不难发现，埃舍尔有效地利用了矛盾空间彰显数学美，具有非常好的视觉效果。

4．拓扑学效果

埃舍尔对拓扑学的视觉效果也很感兴趣。众所周知，拓扑学关注的是空间扭曲后依然不变的性质，这种扭曲可以是弯曲或伸长，但不是崩断或撕裂。早在1946年，埃舍尔在前文所说的艺术作品《骑士平面镶嵌》中，就已经采用了一些具有重要拓扑学价值的形象，在此之后又多次尝试通过艺术作品具体表达数学上的美和有趣。拓扑学的视域是向世界展现那些奇怪的物体，莫比乌斯带就是最具有代表性的例子，它拥有一个特别的性质：只有一个边和一个面。

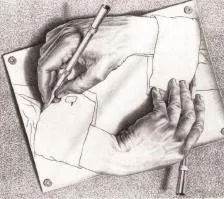
图8

以埃舍尔的艺术作品《莫比乌斯带上的蚂蚁》（如图8所示）为例，如果我们跟踪蚂蚁的路径，就会发现蚂蚁并不是在相反的面上爬行，而是都爬行在同一个面上。这就是埃舍尔艺术作品中展现出的拓扑学价值和数学美。

5．自我复制

埃舍尔的艺术作品总能和数学、信息科学有着千丝万缕的关联，当中一个重要概念就是自我复制，其平版画艺术作品《互绘的双手》（如图9所示）和木版画《鱼和规模》（如图10所示）就用不同的方法表现出了“自我复制”的数学美。

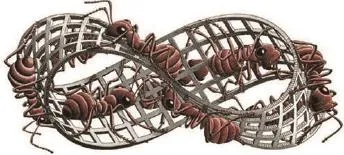
图9

从画面上来看，左手画着右手，右手又画着左手，左右手互绘，埃舍尔好像要表达出“你中有我，我中有你”的意思。我们不难看出，《互绘的双手》的自我复制是直接明了的，双手互绘对方，互绘方式就是意识思考和构建自己的方式。令观众感到自我复制的数学美、神奇之处在于这里两只手的自我和自我复制是完全循环连接在一块的，是同等的。

图10

而在《鱼和规模》这幅艺术作品中，自我复制的数学美发挥了更大的功能，也可称作自我相似。从更深层次水平上讲，自我复制是一种以我们的认知世界互相反映和互相交错的结果。这样的艺术作品所描述的不仅仅是鱼，而是所有的机体。

通过剖析埃舍尔艺术作品中的平面镶嵌、多面体、空间形状、拓扑学效果和自我复制体现的数学美，可以看出艺术作品可以体现数学之美，事物的数学性蕴含着诗意，这不是每个人都能做到的，而埃舍尔从数学思想中获得了巨大的灵感，从生活中的事物的精确、规则、秩序中发现数学美，工作中经常使用直接平面几何和射影几何的结构，这便使他的艺术作品深刻反映了非欧几里得几何学的精髓，其绘画艺术中的数学之美，将绘画艺术和数学进行融合、将自己感悟出的数学美通过错综复杂的视觉效果传达出来，为后人创造出更多充满数学之美的绘画作品提供了非常重要的指导意义。也许，数学是他的艺术之魂，他没有故意表达的数学思想，而是在表达他自己的思想。埃舍尔用他这种独特的理性思维结合他无与伦比的艺术禀赋，为这些抽象的数学美赋予了具体的表象。

[1]朱敏．试议埃舍尔绘画艺术中的数学之美[J]．美术教育研究，016（9）：24．

[2]李凯歌．浅析埃舍尔艺术作品的数学之美[J]．黑龙江科技信息，008（33）：257．

[3]张景中，易南轩．好玩的数学：数学美拾趣[M]．北京：科学出版社，2015．

[4]H．S．M．Coxeter，M．Emmer，R．PenroseandM．L．Teuber，M．C．Escher：Artand．

Science，ProceedingsoftheInternationalCongressonM．C．EscherRome，Italy，26-28March，1985，146-152．

[5]H．S．M．Coxeter，M．Emmer，R．PenroseandM．L．Teuber，M．C．Escher：Artand

Science，ProceedingsoftheInternationalCongressonM．C．EscherRome，Italy，26-28March，1985，287-339．

[6]王众杰，杨敬飞．埃舍尔的魔幻图形及其数学原理[J]．科技信息，2017（1）：82-83．

【本文系基金项目：合肥师范学院2017年度研究生创新基金项目《数学教师入职期关键事件对其成才的作用分析》，项目编号：2017YJS10。】