中心极限定理的实际应用例谈

河南科技学院新科学院 程 楠

中心极限定理的实际应用例谈

河南科技学院新科学院 程 楠

中心极限定理是概率与数理统计学中较为重要的一个内容，它主要是探讨随机变量和的分布以正态分布为极限的一组定理。这些定理是概率与数理统计的一个理论基础，阐明了大量随机变量近似服从正态分布的基本条件。本研究以举例的形式，对中心极限定理的实际应用进行了阐述，旨在为该定理的实际应用提供一定的参考依据。

中心极限定理；实际应用；原理

中心极限定理是概率与数理统计中较为重要的一个知识点，且该知识点是概率论与数理统计之间的一个非常重要的枢纽。该理论指出，大量随机变量之间的加和存在与正态分布相近的分布。所以说，该定理提供了大量独立随机变量之间加和的近似概率的简便方法，而且还很好地解释了大部分自然群体的经验呈正态分布曲线的具体原因，同时，上述结论也促使正态分布的应用变得更为广泛。本研究首先对大数定律与中心极限定理的两大常见定理进行了介绍，然后提出了该定理在实际中的应用情况。

一、大数定律与中心极限定理的两大定理

1．林德贝格·勒维中心极限定理

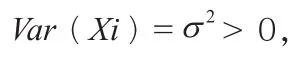
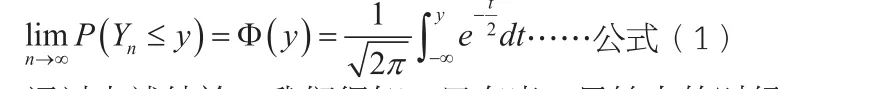
通过上述结论，我们得知：只有当n足够大的时候，Yn才近似～N（0，1）；当n不够大或者较小时，则无法确保上述近似。也就是说：当n足够大的时候，可使用标准正态分布N（0，1）来对与Yn相关事件的概率进行近似计算；而当n不够大的时候，上述计算的近似程度则无法得到保障。当Yn服从标准正态分布N（0，1）的时候，有下式：

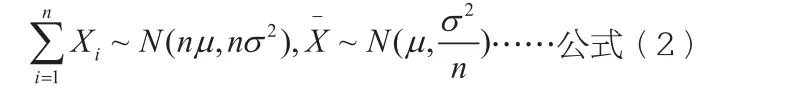
2．棣莫弗·拉普拉斯中心极限定理

定理2：设在n重贝努力试验之中，每次出现A事件的概率为p（p∈（0，1）），现将n次重复试验中A事件出现的次数记为且记：

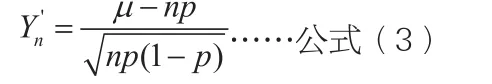
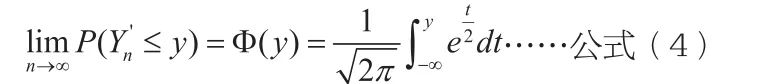
通过上述结论，我们得知：正态分布属于二项分布的极限分布，应用上述结论计算二项分布的概率的前提条件同样是n足够大。

二、中心极限定理的实际应用举例

例1 假设在n重贝努力试验之中，A事件每次发生的概率为0.7，若要使得A事件发生的频率在0.68～0.72范围之内出现变化的概率＜0.9，那么：若要满足上述结论，需要进行多少次重复性试验？

若要解决上述问题，首先应该假设n重贝努力试验中，A事件发生的次数为X，那么根据题设条件可得：X～b（n，0.7）。则有：

E（X）=0.7n，D（X）=0.21n，相对应的概率可表示为X/ n。根据问题要求，若要求出试验次数n，使得P{0.68≤X/ n≤0.72}≥0.90，可使用切比雪夫不等式进行估算，于是得出如下计算式：

那么上式就转化为解不等式1-525/n≥0.9，根据计算可得n≥5250。那么这就是说，至少要进行5250次试验，才能够满足题目中要求的条件。

例2 某工厂一车间现有200台车床，由于相关因素的影响使得这些车床出现停车的情况，现假设每台车床开始运行的概率为0.6，每台车床开始运行时耗电量为1kw·h，且假设每台车床开始运行或者停止运行均为相互独立事件。求至少要供应该车间多少电量，才可使得200台车床以99.9%的概率因不断电而运行？

若要解决上述问题，首先应该假设在任意一个时间点开工的车床的数量为X，那么X～B（200，0.6），np=120，np（1-p）=48，至少需供电量为N kw·h。根据棣莫弗·拉普拉斯中心极限定理可以得出如下公式：

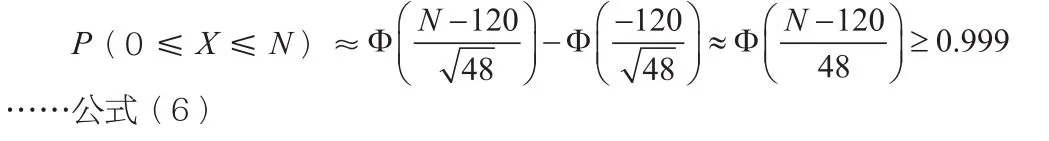
因此，至少供应电量数为141kw·h，方能确保该车间以99.9%的概率不会因供电量不够而对生产产生影响。

例3 现已知某保险公司中有10000名处于同一个年龄范围内的人参加人寿保险，且在同一年之内其死亡率为0.1%，参加此保险的人在每年的元月一号缴纳10元的保险费，若投保者出现死亡的情况，则可向该保险领取2000元的抚恤金。求该保险公司亏本的概率是多少。

若要解决这个问题，首先应该假设在同一年中死亡的人数为X，出现死亡的概率为0.001，那么将10000名在同一年之内是否死亡看成为“10000重贝努力重复试验”，对于10000人的保险费，保险公司总收入为100000元，需要为死者家属提供2000X的抚恤金。那么，保险公司亏本的概率可用下式进行计算：

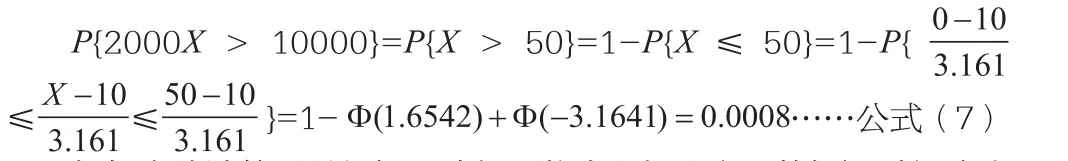
根据上述计算可以得知，我们可将中心极限定理的知识对保险公司的亏本概率进行准确计算，它能够为保险公司提出降低风险因素的决策提供计算依据。

综上所述，中心极限定理是数理统计之中较为重要的一项内容，它以非常严格的数学形式对大样本前提下的数理统计与概率计算进行阐述。无论总体分布状况怎样，在该定理的计算模式下，所选取的样本均值均服从标准的正态分布。该定理在实际生活中的应用较为广泛，为人们的生活带来了极大的便利。

[1]茆诗松，程依明，濮晓龙．概率论与数理统计教程[M]．北京：高等教育出版社，2004．

[2]谢兴武，李宏伟．概率统计释难解疑[M]．北京：科学出版社，2007．

[3]齐治平．概率论与数理统计题库精编（经济类）[M]．沈阳：东北大学出版社，2000．