两点激励中相关系数的影响

农绍宁，赵怀耘



两点激励中相关系数的影响

农绍宁，赵怀耘

（中国工程物理研究院 总体工程研究所，四川 绵阳 621900）

目的用谱函数分析的方式，推导结构在两点激励下的随机振动响应的计算公式。方法通过互谱与相关系数的关系，讨论结构在两点激励下的响应特点。结果对于线性结构，不同相关系数的两点激励下结构激发的模态效果不同，随着相关系数的增大，结构的响应在相邻的谐振峰上，出现增大、减小交替出现的现象。结论相关系数对结构响应影响的特点，应该引起工程结构设计人员的重视。

两点激励；相关系数；随机振动

两点激励是多维激励的一种方式。对于大尺寸结构来说，通常振动环境下结构前后端受到的激励差异较大，利用多台振动器对试件进行多维振动激励方式是更为合理、有效的一种模拟试验方法。GJB 150.16A—2009中对组合式飞机外挂实验也提出了多激励点的要求[1]。由于多维振动与工程实际关系密切，自20世纪60、70年代出现以来，就涌现出许多文献对其进行了研究综述。文献[2]讨论了多轴振动环境试验条件的定义、技术关键以及多轴振动台和振动控制系统的介绍、应用。文献[3]阐述了多维振动试验方法的原理、试验条件定义和试验控制算法。还有许多文献[4—7]对大结构尺寸的具体工程结构进行了数值仿真和实验，结果表明多维振动下结构的响应相对于一致激励有明显的差异，总体上使结构的响应更为复杂。Hao[8]也利用他自己提出的相干函数模型计算了圆拱的多点输入响应，发现如果忽略地震动之间的相干，则求得结构的响应有时偏高，有时偏低，但未能给出普遍的规律。

文中基于随机振动的理论，用谱函数分析的方式，推导结构在两点激励下的随机振动响应。利用互谱与相关系数的关系，讨论了结构在两点激励下不同相关系数的响应特点，认为相关系数对结构的响应有较大的影响，给出了一些有意义的结论。

1 两点激励随机振动响应谱

为简化分析，以长度为的简支均匀梁位移响应为例说明，如图1、图2所示。

图1 左支座基础激励

图2 右支座基础激励

对于图1左支座基础激励，左支座基础位移为0L时，杆长处静态位移为；对于图2右支座基础激励，右支座基础位移为0R时，杆长处静态位移为。

使用相对位移，即设相对位移为，动力学方程为：

式中：为单位长度质量；为阻尼系数；为弯曲刚度；为第阶模态。

质量归一化的模态为：

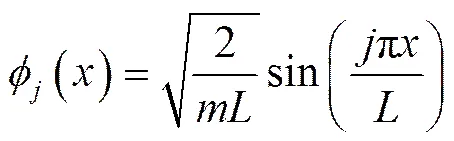
以左端为例：

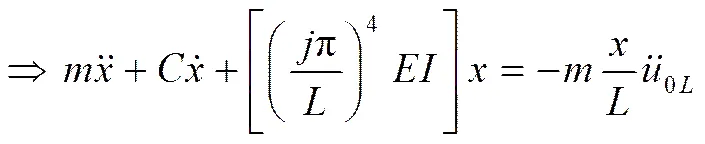
应用模态正交性（仍用变量表示）：

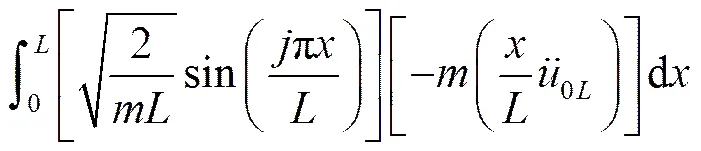
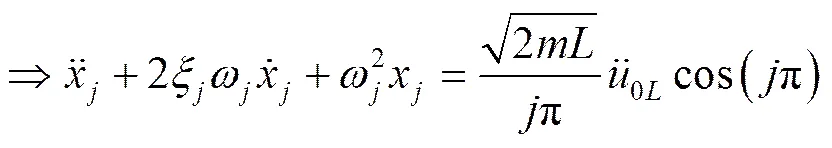
同理，对于右端：

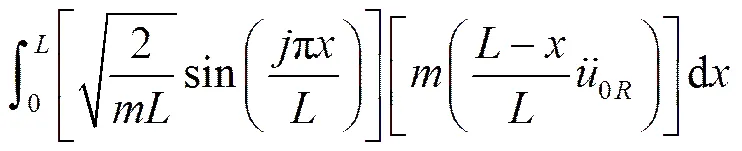
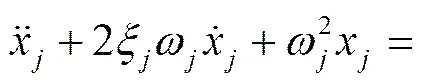
应用杜哈曼积分：

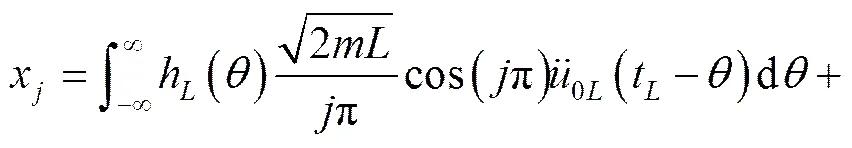
方程的解为：

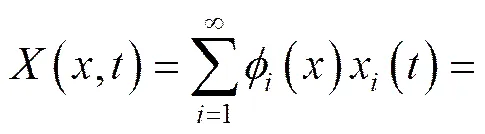
方程两边取相关函数：

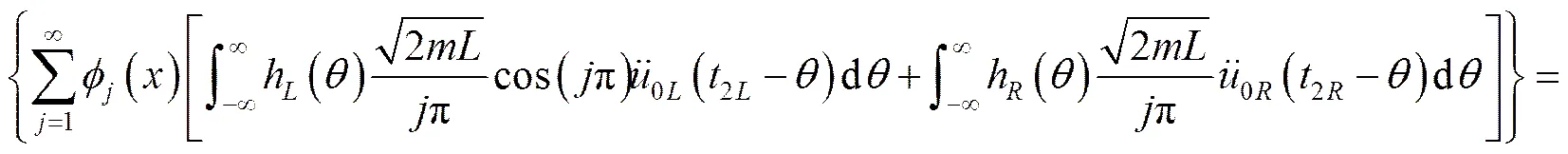
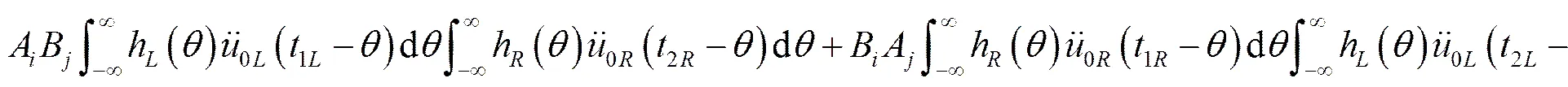
方程两边做傅里叶变换：

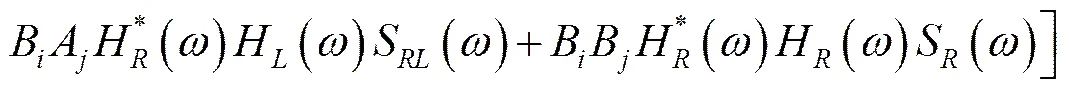
其中：

，，，，

式中：“*”代表共轭；S()为左端输入加速度谱；S()为右端输入加速度谱；S()和S()为两端输入加速度互谱。

2 互相关系数与互谱

每个激励力函数，因为是随机过程()，在不同的时刻值是随机变量，总有自己的相关函数，也就是自相关函数R()。

同理，两个随机过程()和()，它们在不同的时刻值是随机变量，可以定义这两个随机变量函数的二阶联合矩：

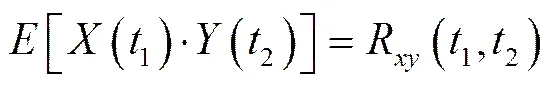
式中：R(1,2)为随机过程()和()的互相关函数。

定义无量纲的标准互相关函数：

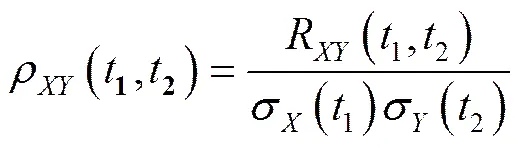
式中：σ(1)，σ(2)为随机过程()和()的标准方差。

若互相关函数ρ(1,2)不恒等于零，则随机过程()和()是相关的，若互相关函数ρ(1,2)恒等于零，则随机过程()和()是不相关的。

对于各态历经的随机过程，随机过程()和()的标准方差不随时间变化，为一个确定的值σ和σ。随机过程()和()的互相关函数R(1,2)为时间差=2－1的函数，当时间差固定时，互相关函数R(1,2)为一确定的值R。因此，同随机变量相似，互相关函数为时间差的函数。

对比相干系数：

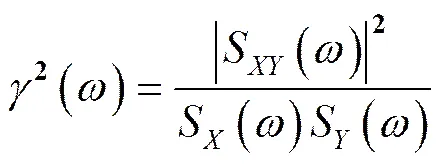
两者是相似的，其中S()为R()的傅里叶变换。

因此相干系数也可以表征两个各态历经随机过程()和()的相关程度。一般来说，相关程度越高，相干系数值越大，S()的值也较大。

3 互相关系数的影响

忽略≠的交叉项影响，响应简化为：

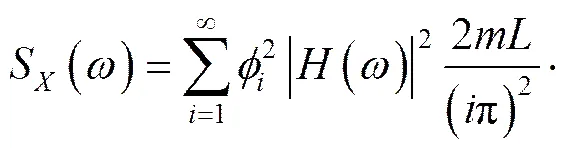
可见，响应与模态阶数有关，还与互谱S()的大小有关。特别的，当两点激励完全相关时，则，响应。在时，响应为0。

4 工程实例

对某挂框式夹具进行了两点激励振动实验[9]。挂框式夹具两点激励振动试验安装状态如图3所示，测点布局如图4所示。

图3 挂框式夹具两点激励振动实验安装状态

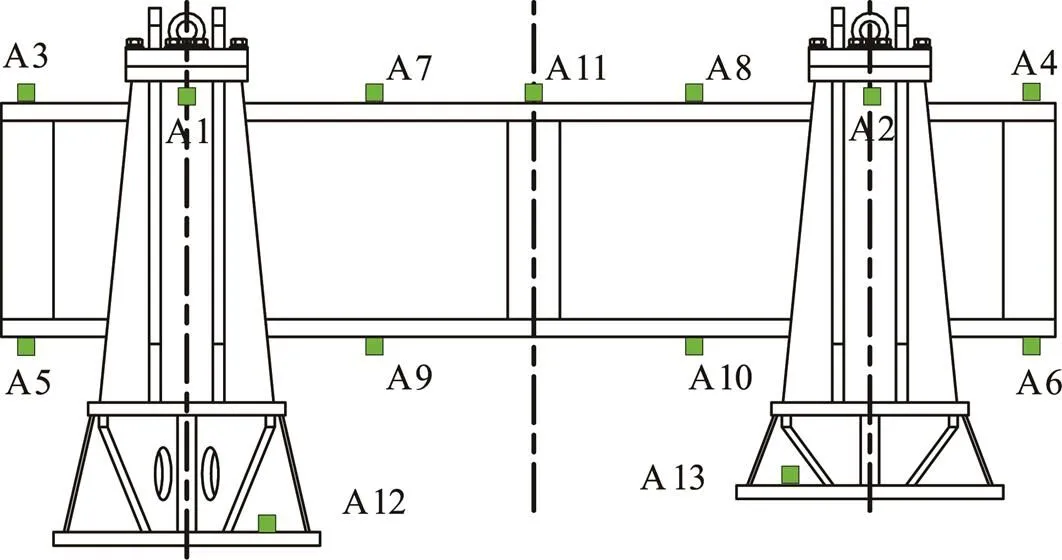
图4 挂框式夹具两点激励振动实验加速度测点布局

分别设置了互谱S()为0.0，0.3，0.5，0.9，以结构上A5测点为例，不同的互谱值，即不同的相关系数下响应见图5。在其中的一个谐振峰上，随着相关系数的增大，响应值越大；而在相邻的谐振峰上，随着相关系数的增大，响应值越小。

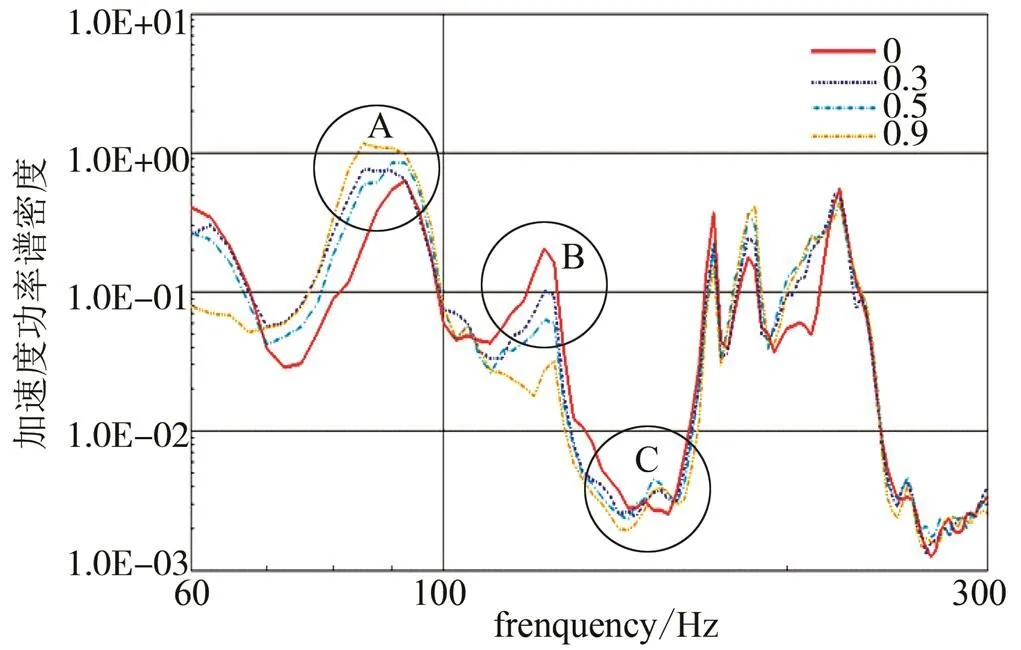
图5 不同相关系数A5测点响应

根据理论计算结果，结构在143 Hz附近有谐振响应，但结构上（例如A5测点）在143 Hz附近响应很小（见图5C处），对应了cos(π)= －1时的结果，如图6所示。

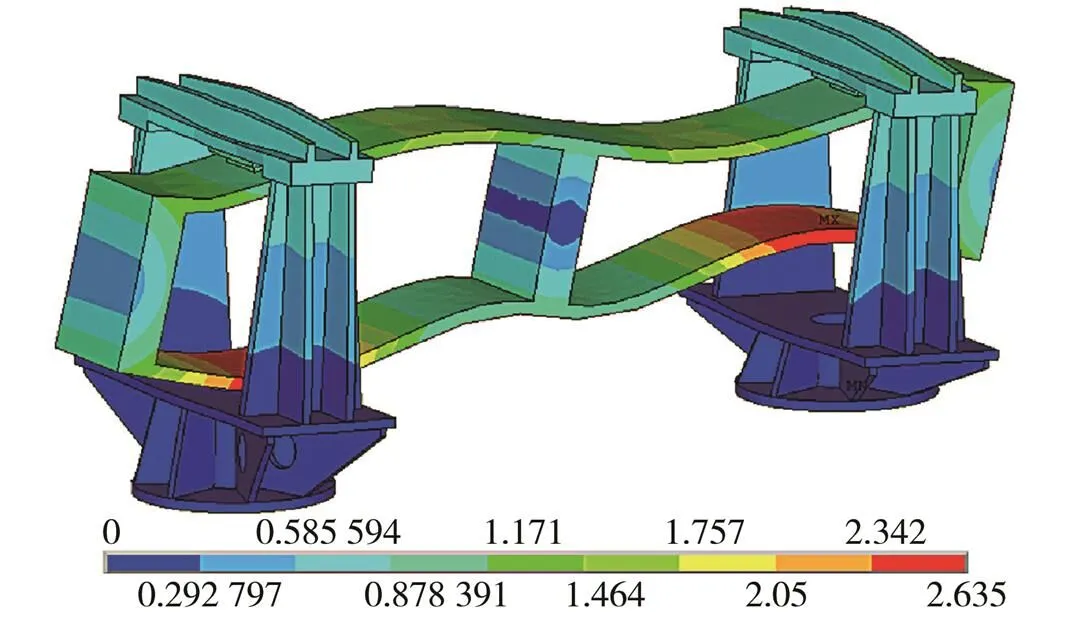
图6 143 Hz模态响应

5 结语

文中利用谱函数的形式，给出了两点随机激励下结构响应的一些特点。从相关系数方面分析了结构响应差异的这一因素。随着相关系数的增大，结构在相邻的谐振峰上，响应随之增大、减小交替出现。在激励谱满足一定的条件下，结构响应可能在某些模态的响应为0。尽管提倡采用多点激励的方式以利于激发出更多的结构模态响应，但也可能出现模态响应为0的现象。两点激励振动响应的这些特点可为工程结构设计人员提供参考。

[1] GJB 150.16A—2009 军用装备实验室环境试验方法第16部分: 振动试验[S].

[2] 夏益霖. 多轴振动环境试验的技术､设备和应用[J]. 导弹与航天运载技术, 1996(6): 52-59.

[3] 吴家驹, 荣克林. 多维振动环境试验方法[J]. 导弹与航天运载技术, 2003(4): 27-32.

[4] 白凤龙, 李宏男. 地震动多点激励下大跨空间网架结构的反应分析[J]. 工程力学, 2010, 27(7): 67-73.

[5] 武芳文, 薛成凤, 赵雷. 多维地震激励作用下大跨度斜拉桥的随机响应[J]. 武汉理工大学学报, 2010, 32(9): 344-347.

[6] 柳国环, 李宏男, 田利. 九江长江大桥在多点多维地震激励下的反应分析[J]. 振动与冲击, 2009, 28(9): 204-209.

[7] 陈颖, 田光明, 钟继根. 典型细长体结构的两点激励振动试验设计[J]. 航天器环境工程, 2013, 30(1): 68-71.

[8] HAO H. Ground Motion Spatial Variation Effects on Circular Arch Response[J]. Journal of Engineering Mechanics, 1994, 120(11): 2326-2341.

[9] 赵怀耘, 田光明, 钟继根. 两点激励振动试验时结构模态对控制效果的影响分析[J]. 装备环境工程, 2012, 9(6): 51-53.

[10] GEORGE A H, RICHARD S S, MARCOS A U. A Review of Multiaxis/Multiexciter Vibration Technology[J]. Sound and Vibration, 1996(4): 20-27.

[11] 王梦魁. 多维振动环境试验的实践[J]. 装备环境工程, 2005, 2(3): 23-25.

[12] 美国ANSYS公司北京办事处. ANSYS动力学分析指南[K]. 北京: 美国ANSYS公司北京办事处, 2000.

Influences of Correlation Coefficient in Two-point Excitations

NONG Shao-ning, ZHAO Huai-yun

(Institute of Systems Engineering CAEP, Mianyang, 621900, China)

Objective The paper aims to derive the computational formula for random vibration response of structures under two-point excitations with spectrum function. Methods Response characteristics of the structural under two-point excitations were discussed with cross spectrum and correlation coefficient. Results For linear structures, the stimulated modal effects varied with different correlation coefficients under two-point excitations. With the increase of the correlation coefficient, the structural response spectrum increased and reduced alternately on adjacent resonance peaks. Conclusion Influences of structural vibration response character with different correlation coefficient should be worth of attention of the designers of engineering structures.

two-point excitation; correlation coefficient; random vibration

10.7643/ issn.1672-9242.2017.08.006

TJ01；O322

A

1672-9242(2017)08-0030-04

2017-04-05；

2017-04-25

NSAF基金项目(U1430129)

农绍宁（1975—），男，广西崇左人，硕士，高级工程师，主要研究方向为工程力学。