基于仿真的动态环境试验设备系统设计

牛宝良

基于仿真的动态环境试验设备系统设计

牛宝良

（中国工程物理研究院总体工程研究所，四川 绵阳 621900）

目的 介绍计算机仿真技术的特点及其在动态设备系统设计中的应用。方法 首先简要介绍仿真技术的发展和特点，其次介绍一些仿真经验，最后通过若干实例介绍Simulink软件在动态设备系统中的应用。结果 基于Simulink仿真，可以快速获得系统运行过程中的各种所关注的参数运行结果，为系统性能评估和优化提供可靠的依据。结论 计算机仿真技术已经日趋成熟，应用于动态环境试验系统设计中，可提升设计水平。

仿真；动态系统；代数环；环境试验

环境试验设备中，振动、冲击、加速度、摇摆试验设备等都属于动态试验设备。动态试验设备系统的特性一般比较复杂，多个参数相互耦合，且往往是频率的函数，这给系统的设计带来困难。早期的设计技术只能采用简化的基于解析公式的设计计算，以液压振动台的伺服阀为例，计算输出流量时不考虑负载影响、或者负载按某个固定值来处理，而实际上，负载是时时刻刻都在变动中。伺服阀随着频率的增加，流量会衰减，相位滞后也会不断增加，相位滞后对系统的稳定性也会有显著影响。这样一种处处简化的设计手段，对系统动态特性的预估和了解是粗糙的、不全面的。因此也增加系统设计的风险。

仿真技术是分析动态系统的有效手段，它把各种相关的动态变量放到一组微分方程中，用模型（电路或者软件）表达系统的动态特性，运行模型得到各量随时间的变化曲线。后期随着全数字仿真技术的发展，不仅仅是微分方程，各种非线性环节或者模块也都可以进到系统模型中，因此逼真程度进一步提高。随着微型计算机和仿真软件的普及，仿真技术在各行各业应用越来越多。文中通过若干实例介绍仿真技术在动态环境试验设备设计中的应用。

1 计算机仿真技术历程与现状简介

仿真技术经历了模拟计算机、数字模拟混合计算机、全数字计算机三个大的阶段[1]。1946年，一台能够模拟导弹、飞机飞行轨迹等物理现象的模拟计算机在美国问世。标志着模拟仿真技术的开始。此后，涌现了大量的模拟机，20世纪50年代至60年代初是模拟计算机的黄金时期。尽管模拟仿真计算机取得了巨大的成功，但也暴露出数据精度不够、实现插值函数困难、不能满足数字控制系统的需要等问题。20世纪50年代末，由于导弹技术发展的需要，促使了混合仿真计算机的诞生。20世纪60年代至70年代中叶是混合仿真计算机的鼎盛时期。美国ADI公司1978年研制出全数字仿真计算机AD10，它的诞生标志着在那场混合仿真计算机与数字仿真计算机的激烈竞争中，全数字仿真计算机终领风骚，也标志着全数字仿真新时代的来临。1973年美国研制成功专用液压仿真软件HYDSIM，之后欧美各国不断发展完善液压仿真软件，1980年代先后推出了DSH（德国）、HASP（英国）等软件。

1985年10月15日，我国第一台全数字仿真计算机“银河仿真I型计算机（YH-F1）”研制成功，标志着中国进入全数字仿真时代。此后又有多个新型的仿真计算机问世。

航空、航天是最先开始应用仿真技术的几个传统领域，是仿真计算机诞生的摇篮。也只有这样的一些重要的、复杂的动态系统设计才用得起。

仿真技术的普遍应用则是在微型计算机普及和仿真软件的图形化编程之后，标志性的节点是MATLAB/Simulink仿真软件的推出。MATLAB/Sim- ulink在仿真软件中具有非常重要的地位。可以认为Simulink是一个分水岭，之前建模是基于语句描述，模块之间的关系靠语句定义，不能直观看到系统的模块组成和模块之间的关系。Simulink提供了图形化的建模方式，只要进行鼠标的简单拖拉操作就可构造出复杂的仿真模型。它外表以方块图形式呈现，且采用分层结构。从建模角度讲，这既适于自上而下（Top-down）的设计流程（概念、功能、系统、子系统、直至器件），又适于自下而上（Bottom-up）逆向程序设计。从分析研究角度讲，这种Simulink模型不仅能让用户知道具体环节的动态细节，而且能让用户清晰地了解各器件、各子系统、各系统间的信息交换，掌握各部分之间的交互影响。这给建模带来极大的方便，也有利于模型的查错和修改。除了建模快捷方便外，其他功能也很强大，它可以处理的系统包括：线性、非线性系统；离散、连续及混合系统；单任务、多任务离散事件系统。 Simulink 6.5是里程碑版本，它的加速模式能使运算速度提高几十上百倍。

除了MATLAB/Simulink外，还有一些仿真软件，比如AMESim 是当今领先的传动系统和液压/机械系统建模、仿真及动力学分析软件。再比如ADAMS，是应用较多的一种动力学仿真软件。比如Modelica，是所谓的多领域建模软件。它们各有特色，或者对某领域有特别的优势，或者多学科综合建模方面有优势。

实时仿真系统也是仿真系统的一个重要分支，不仅要求获得系统响应，而且要求响应与仿真对象实际的响应时间是严格的1:1。当具有这样一种时间上的1:1特性时，就可以与真实的硬件系统连接，构成所谓的硬件在环仿真系统。这类系统通常都不是普通PC所能胜任的，需要专门的比较高端的硬件系统。国内外也都有相应的产品，国外产品有dSPACE，RT-LAB等，国内的有国防科技大学的KDRTS、西安二炮工程学院的CHY-Ⅲ、航天三院的海鹰实时仿真工作站、西北工业大学的并行计算机PD-100、北京华力创通科技有限公司的HRT1000、北京广思特公司的半实物仿真系统、北京经纬恒润科技有限公司的Higale半实物仿真系统等。

在环境试验设备领域的仿真，应该说起步不算晚，李坦在1985年就在模拟计算机上开展了液压振动台的仿真[2]，但是由于仿真软硬件等不成熟不方便等原因，并未大量普及。大约在2000年之后，仿真应用逐渐多了起来。2010年之后，特别是近几年，进入了普遍应用阶段[3—7,9—16]。

如今MATLAB/Simulink仍然是工程技术人员喜欢的仿真软件之一。文中基于MATLAB/Simulink来介绍若干仿真实例，展示仿真给环境试验设备设计带来的便利。

2 仿真技术应用实例

2.1 仿真的几个基本概念

2.1.1 连续与离散

以单自由度振动系统为例，它的运动方程是

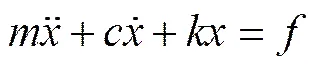
式中：为质量块的质量，kg；为运动阻尼，N/(m·s－1)；为弹簧刚度，N/m；为质量块的位移，m；为的二阶导数，表示加速度，m/s2；为的一阶导数，表示速度，m/s；为作用在质量块上的力，N。

对应的拉氏变换的表达式为：

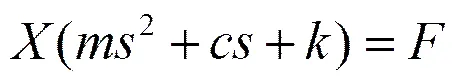
式中：是位移的拉氏变换；是力的拉氏变换。

式（2）对应的模型就是连续模型，它的Simulink模型可以用连续积分器1/构建，如图1中的上面一个模型。把式（2）离散化（有多种离散办法，应用较多的是Tustin变换），或者用连续积分器替代连续积分器1/s。这里用替换法，用梯形积分（Simulink还提供了前向积分、后向积分，都属于矩形积分，精度比梯形积分差）替换连续积分，所得模型如图1中下面一个模型。从模型形式上看，连续系统用的变量，离散系统用的变量。在内部解算上，连续系统有多种解算方法可选，而且这些算法一般都是变步长的多步算法，离散系统的算法则是定步长单步法。

采用离散系统建模有以下好处：离散系统支持Simulink的加速度模式，仿真速度快；单步法，运算量是固定的，仿真耗时也是固定的；半实物仿真系统必须是离散的，采用离散建模方便转换到半实物仿真系统；记录的响应数据是等间隔的，便于后续处理。文献[11]给出了详细实现方法。

当用离散积分器（梯形）替换完连续积分器1/之后，点击运行，会提示“The model 'xxx' has an algebraic loop. Accelerator mode is not supported for models with algebraic loops.”，意思是模型有一个代数环，加速模式不支持代数环。

2.1.2 代数环

尽管离散系统有上述的好处，但是代数环是个问题。所谓的代数环，就是模型有环路（有反馈必然有环路），求解当前某个变量时，又要用到这个变量。对于动态系统，这几乎是必然要遇到的。解决代数环有几个办法，最简单的办法是加延迟环节，或者积分器采用前向欧拉法（Forward Euler）。这些方法精度不高，有时还会发散。笔者提出了一个预测法，较好地解决了代数环。所谓的预测法，就是用前面若干点预测当前点的值。相应的Simulink模型见图2和图3。

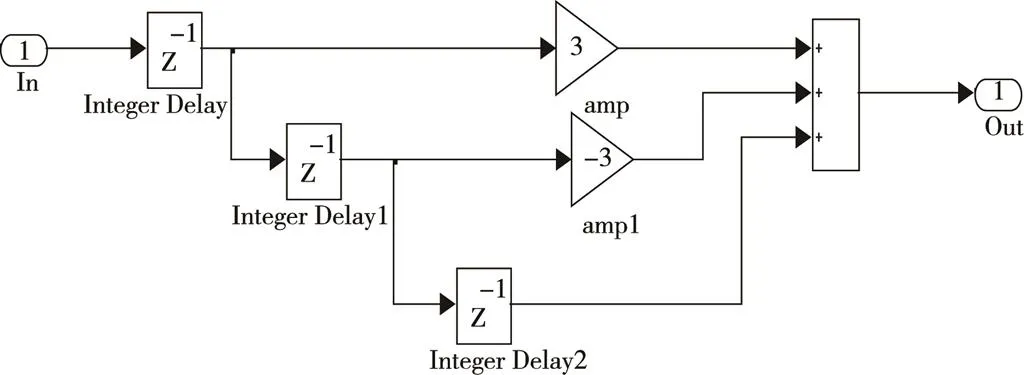
图2 预测环节

注意：预测环节中有三个延迟器，如果知道初值，比如图1所示的例子，加速度初值是一个重力加速度，就可以把它们的初值都置为9.806 65 m/s2；如果不知道初值，就置为0。带来的后果就是仿真开始的几个数据点不正确，之后就正确了，基本不影响仿真。

把这个模块（模块名pred）插入在mass1后面，见图1下面的一个模型，代数环的问题就解决了。

对图1所示的仿真模型，给定一组参数，＝10 kg，＝39478 N/m，＝125.66 N/( m·s－1)，可以仿真得到连续系统、离散系统的仿真结果，见图4和图5。可以看到，步长合适的情况下，连续系统、离散系统结果在采样时刻是一致的，离散系统仿真结果波形是阶梯状的。这个模型同时也显示了Simulink其实是可以在一个模型里同时有连续系统、离散系统。

2.1.3 采样间隔

当采用离散建模时，采样间隔是一个很关键的参数，采样间隔的倒数是采样频率。一般来说，采样频率与系统中振荡环节（也称二阶环节）的共振频率相关。首先，为了能看清振荡的响应，采样频率应该是振荡环节的共振频率的10倍以上。其次，为了仿真系统运行稳定（不发散），采样间隔也应减小。越小的采样间隔，一般精度越高，但同时仿真一次的耗时越长。因此，仿真间隔也是要从这两方面取舍。通常可以先取1×10－4s或者1×10－5s，不行再调整。

2.1.4 上采样、下采样、抽取

一个物理系统，有时由快慢相差很大的模块构成，这时如果采用统一的采样间隔，那就只能确保快的模块，即采样间隔取小值。这样一来，对于慢模块来说，数据量就很大，许多数据是多余的，而且容易导致计算机内存溢出。

一种办法就是采用抽取，即在示波器、数据保存模块中，设置Sampling参数的Decimation,比如设置Decimation值为100，表示每运算100步，记录1个数据到示波器、数组、或者文件中。这种办法数据量可以减下来，但是模型计算量一点不减少。

另一种办法是采用上采样、下采样的办法。即慢速模块用一个比较大的步长，而快的模块用一个小的步长，慢模块的输出进到快模块前用上采样（Upsample），快模块的输出进到慢模块前用下采样（Downsample）。Upsample、Downsample在Signal Processing Blockset下的Signal Operations目录下可以找到。下采样模块直接使用没有问题。上采样模块不能直接使用，因为它是采用加0的办法提高采样频率，把一个连续的信号变成了脉冲信号，如图5的上图所示。笔者给出了修正的上采样模块，如图3所示，得到的上采样后的波形如图5的下图所示。这样，慢模块的运算量的减小了很多，整个系统的仿真速度就能大幅提高。

总之，适当设置抽取参数、采用上采样、下采样有利于避免内存溢出，有利于减小数据、方便后续处理和显示，有利于提高仿真速度。抽取的原则是信号的每个周期有10～100个数据点为佳。点数再少波形就太粗糙，点数再多也没有太大意义。对于扫频信号，只能按最高频率来设置。

避免内存溢出的另一个办法是在示波器上勾选（limit data points to last）选项，填写数据点数，只保留仿真最后的若干数据点。把数据写入文件既能把全程数据保留下来，也不会导致内存溢出。

2.1.5 单位

单位其实很重要。由于历史原因，各种非国际单位制的单位仍没有完全淘汰，再者，有些单位比较直观方便，仍在使用。笔者的观点是方便的或者习惯的单位可以用，但是进入仿真程序时一律换算为国际单位制，仿真结果用于显示时，可以再换算为日常习惯的单位。比如加速度，通常习惯用作单位，仿真时必须换算为m/s2，流量用L/min，仿真时必须换算为m3/s。有些弄简成繁的单位，比如质量用kg·ｓ2/cm，则应坚决淘汰。单位正确是仿真结果正确的重要保证。

2.2 液压振动台

液压振动台在装备环境试验、汽车道路模拟试验、地震模拟试验等方面广泛应用。虽然技术指标有所不同，但是主要构成、控制原理是相同的。下面以某10 t振动台为例介绍仿真的应用，结构如图6所示。主要参数：位移为±120 mm，速度为1 m/s，加速度为10，负载为1 t。

液压振动台设计最主要的参数就是活塞有效面积，传统的设计是基于最佳功率匹配原则[8]，或者简单的负载压强＝2/3油源压强。基于仿真的设计，可以以2/3原则计算初值，通过仿真全面了解在整个频带上的效果，然后再进行迭代。液压台的流量也是系统的主要参数之一。有文献分析过，共振频率处最低，超过共振频率后，逐步上升。通过仿真可以了解全频带的流量需求。建立的液压振动台Simulink模型如图7所示。

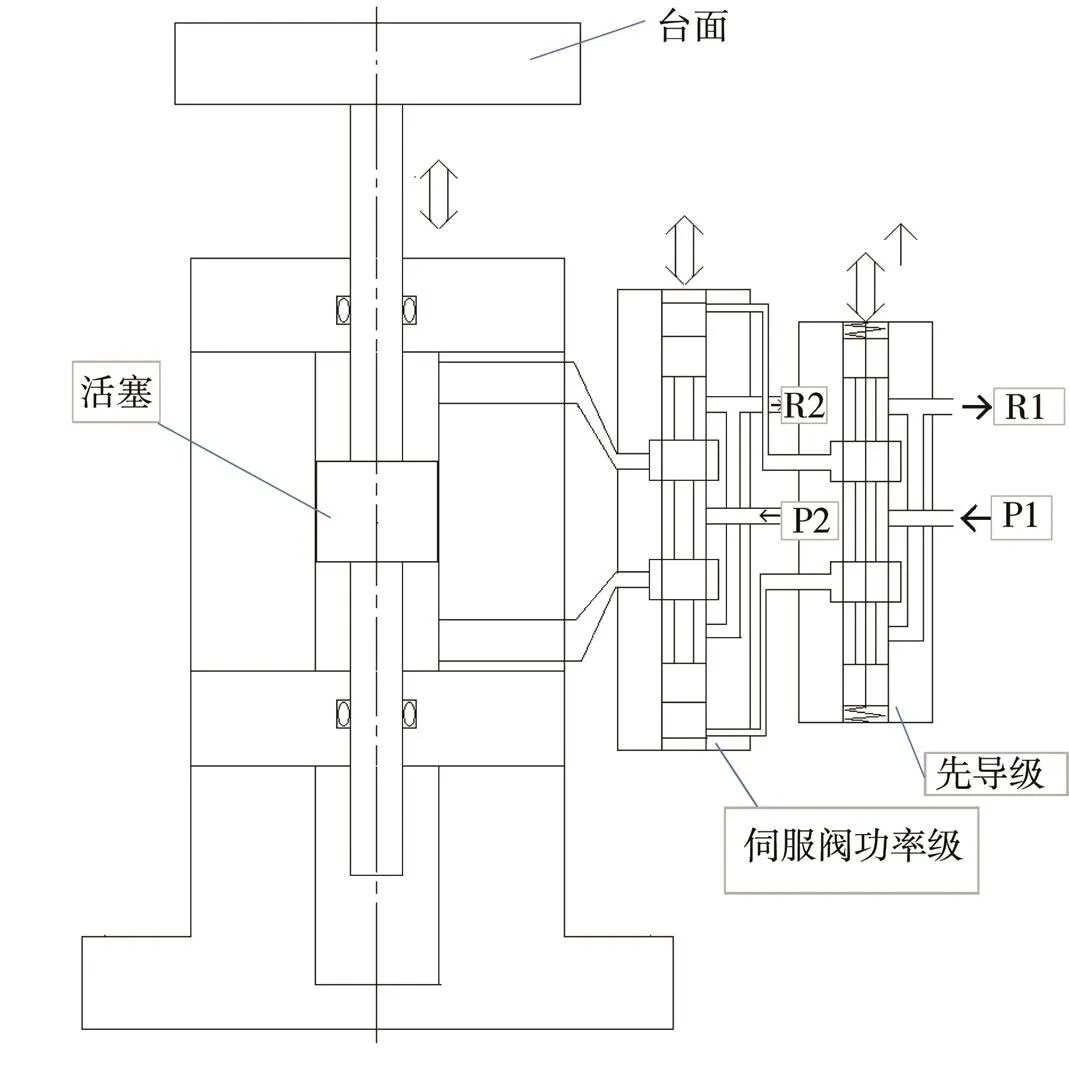
图6 液压振动台结构

利用该仿真模型可以仿真研究[9]：理想情况下的性能；活塞摩擦对波形的影响；基础质量对波形的影响；控制算法对性能的影响；伺服阀遮盖对波形的影响；负载振动频率特性；基础的振动响应。

这里仅介绍两种三状态控制仿真情况。一种是电压输入，一种是加速度输入。

电压输入时，希望最大电压在不同频率对应不同的量的最大值，低频10 V对应最大位移，中频段，10 V对应最大速度，高频段，10 V对应最大加速度。这样既能发挥振动台的最大能力，也不会因为饱和削波导致波形失真。优化后的效果见图8。

另外一种是加速度输入，给定的输入信号与目标加速度信号成比例，控制器优化的目标是让响应加速度尽可能逼近给定加速度。从传函来说，希望传递函数接近一根平直的直线。优化后的某地震波控制如图9所示。由于低频段受位移限制，加速度很小，所以采用加速度输入进行地震波试验时，必须先做一次三参量生成，看看位移、速度是否超振动台极限，确认不超极限时，方可进行试验。

2.3 二维摇摆试验机

二维摇摆试验机是中国工程物理研究院总体工程研究所研制的一套试验系统。在研制阶段进行了仿真分析，其结构和仿真模型如图10和11所示。

系统主要参数：运动自由度为两自由度，即可同时进行横摇和纵摇；最大负载质量不小于1 000 kg；负载高度极限不低于2 200 mm；台面尺寸不小于 2 200 mm×2 200 mm；负载质心高度极限不低于1 000 mm；倾斜试验能力，最大横倾角为±45°，最大纵倾角为±30°；摇摆试验能力，最大横摇角为±60°、横摇周期为3～14 s，最大纵摇角为±30°、纵摇周期为4～10 s；倾斜摇摆复合试验能力（配30°倾斜夹具），最大横摇角为±60°、横摇周期为3～14 s，最大纵摇角为±15°、纵摇周期为4～8 s；

通过仿真，得到如图12所示的阀流量、角位移，得到图13所示的负载角速度、驱动力矩、机械功率，以及其他关注量，比如跟踪误差、齿隙对摇摆角度影响等。对阀选型、供电功率配置等提供了有力支撑。

2.4 离心机

中国工程物理研究院总体工程研究所2号离心机，容量为200t，最大离心加速度为200。系统结构主体见图14。系统的仿真模型见图15。细节可参考文献[10—12]。

通过仿真，可以确定多大的上升速率可行，或者给定的一个上升速率，需要的多大电压、电流。如图16所示。也可以为新离心机设计提供支撑。

2.5 游戏机

某升降游戏机的结构如图17所示。负载为4 000 kg，最大升程为20 m，通过滑轮组实现3倍的位移放大。负载通过两根钢丝绳提升，相当于每根钢丝绳承受0.5倍载荷。

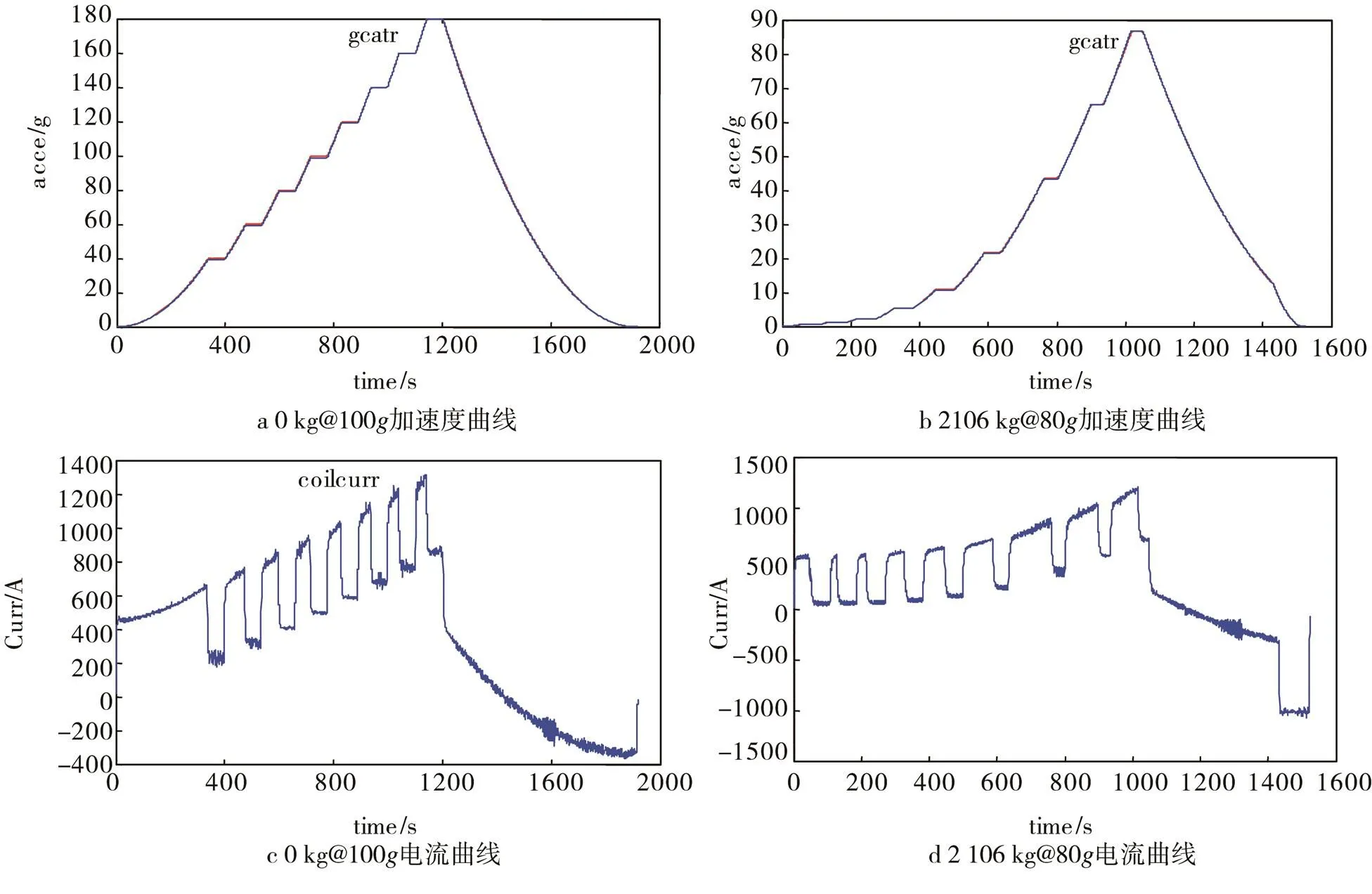
图16 加速度、电流时域曲线

系统仿真模型如图18所示。包括信号源、控制器、伺服阀、振动系统等几个模块。控制器采用PIDF控制算法。伺服阀采用双出口伺服阀模型，液压缸采用单出杆模型，可真实反映上下两腔的油液压强及液压缸的输出力。振动部分用钢丝绳把液压缸活塞和负载连接，钢丝绳用单边刚度弹簧表示，只承受拉，不承受压，压刚度为0。现通过仿真设计系统的主要参数，比如可实现的加速度、液压伺服阀的流量、液压缸的缸径杆径、油源的压力、流量、一次升降需要的油液等。

通过多次迭代优化，确定伺服阀额定流量为800 L/min，油源压力为21 MPa、流量为600 L/min。负载运动的位移、加速度见图19。

可以看到，负载较好跟踪了给定位移，有三个时刻达到失重（－1加速度），钢丝绳峰值载荷为81.26 kN。作为游戏机，主要是给游客加速度感觉，这样的结果是满意的。如果是作为工业控制，需要精确跟随给定位移，有若干办法来提高精度，比如增加活塞面积、改变钢丝绳刚度、尝试不同的控制策略和控制参数等。

3 对仿真的再认识

仿真技术的作用已经无需质疑，对于复杂系统，通过仿真可以提高设计效率和质量，节约研制经费。在此，简要总结一下对仿真的几点认识。

1）深化对系统的认识。仿真模型的建立依赖一定的科学规律，而这些科学规律往往是理想条件下对单一问题的科学表述，比如牛顿第二定律=，黏性阻尼力=·，弹性定律=。一个单自由度系统，包含了上述三个规律，理想情况下可以得到解析式。如果阻尼力是=·v，或弹簧力=kx，或弹簧是钢丝绳类（受拉有刚度，受压刚度为0），或很多的自由度，解析表达式就可能得不到，因而也就不能得到其响应和认识其规律。这些对于仿真来说，则是非常容易的。因此，科学规律是建模的基础，而建模与仿真可以获得对系统更深入全面的认识。

2）系统参数设计与优化。当给定一组设计目标参数后，基于建模仿真，就可以得出系统相关的许多参数，比如液压振动台设计，通过仿真可以得到基础质量、油源压力、电源功率等一系列外界供给参数，由此分析系统的建造规模、经费等。通过多轮次迭代，可以进行优化，以最低的成本获得最大收益。

3）控制器设计与优化。含有控制系统的试验系统，其控制系统往往成为系统的核心子系统，它的算法决定了系统的稳定性（稳定余度）、控制精度等。在仿真系统不用担心系统不稳定导致的设备损坏；可以施加多种不同的载荷，检查控制算法的适宜性；算法、控制器参数、被控对象等的修改只需修改仿真模型，操作快速。整个过程安全、便捷、高效。

4）故障与异常分析。对于真实的系统，人为制造某种故障检查系统的反映是有很大风险的，在仿真系统中，则不存在任何风险。可以安全、方便地观察系统的反应、故障联锁机制是否起效。

5）人员培训。比较操作复杂的重要系统，比如飞机驾驶、高铁驾驶、核电站的操作，采用仿真机进行培训，是安全、高效、节约的培训方式。

6）分析工程因素的影响。在做系统设计时，往往用的理想模型。比如伺服阀，理想情况是零遮盖。实际四个节流边的遮盖量肯定是非零的，且不相同。可以建立双出口四边滑阀模型，人为给定不同的正负遮盖量，通过仿真看看它们对系统波形失真、控制精度等的影响。再比如摩擦力，分析原理时往往不考虑摩擦或者给一个固定的摩擦力值，实际上与加工间隙或过盈量、密封件的材质、压缩量等都有关系，可以人为给一些不同的摩擦力，看看对系统性能的影响，或找到摩擦力允许的上限值。

7）仿真的“真”与“不真”。在正确建模的情况下，可以说仿真得到的规律是“真”的，仿真的值是“不真”的。因为如果模型正确，仿真结果就能反映系统主要运行规律。如果模型不正确，规律也就不正确了。

以液压振动台为例，用二阶振荡环节表示一个伺服阀时，振动波形不失真，与实际系统相差甚远。因为模型已经忽略了阀压降这样一个显著的非线性因素。加上阀压降这个非线性因素，则振动波形失真特性就能显示出来。再以摩擦为例，不考虑摩擦，则波形光滑不失真。加上摩擦这个实际存在的因素，结果就与实际相近，如图20所示。

实际的系统是非常复杂的，常常不愿或者不能建立反映每个参数细节的模型。以液压缸的摩擦为例，具体每个液压缸的摩擦力都是不一样的（每个液压缸的密封圈槽尺寸有加工误差、每个密封圈有加工误差、运行温度也会影响密封圈的压缩量）。再以油液粘度为例，它是温度、压力的函数，建模时也常常把它当作常数，也会带来误差。伺服阀的频率特性每一台各有不同，即使是同一台，它的频率特性与流量幅值还有关系，小流量频响范围宽，大流量频响范围小等。这些因素导致仿真输入参数与实际存在差异，因此仿真的值是“不真”的，但是这个所谓的不真，是有限度的，不能因此而否定仿真。

总之仿真可以反映系统的主要、基本的规律，得到的结果具体值与实际系统会有差异，认识这点，才能正确看待仿真技术。

4 结语

文中简略回顾了仿真技术的仿真历程，给出了一些经验和若干仿真在环境试验设备方面的应用实例，总结了仿真技术的认识。从中可以看出，计算机仿真技术在环境试验设备研制中大有作为，将来伴随着仿真技术的发展，环境试验设备研制也会越来越快速、准确。

[1] 李兴玮, 曹娟. 仿真计算机的过去､现在和未来[J]. 系统仿真学报, 2009,21(S2): 106-111.

[2] 李坦. 位移及加速度控制的液压伺服振动合的动态优化设计[J]. 试验机与材料试验, 1985(2): 15-22.

[3] 李长安, 王长江, 何长安. 不对称结构的防滑刹车压力伺服阀的仿真研究[C]// 97中国航空学会液压与气动专业学术讨论会. 1997.

[4] 吴志清. 四通阀控非对称液压缸伺服系统的动态特性[J]. 煤矿机械, 2004(7): 32-34.

[5] 江桂云, 王勇勤, 严兴春. 液压伺服阀控缸动态特性数学建模及仿真分析[J]. 四川大学学报(工程科学版), 2008(5): 195-198.

[6] 任杉, 李玮, 韩青. 基于MATLAB 的阀控缸伺服系统仿真分析[J]. 装备制造技术, 2009(9): 32-33.

[7] 徐敏, 薛敏东, 王曦. 喷嘴挡板式力反馈电液伺服阀非线性动态模型[C]// 2010年中国国防科技会议. 西安, 2010.

[8] 关景泰. 机电液控制技术[M]. 上海: 同济大学出版社, 2003.

[9] 牛宝良, 王珏. 液压振动台时域建模与仿真[J]. 装备环境工程, 2010, 7(6): 247-251.

[10] 钮王杰, 张斌超, 刘春艳. 基于MATLAB/Simulink转速闭环直流调速控制系统的仿真研究[J]. 山西大同大学学报(自然科学版), 2011, 27(5): 33-35.

[11] 牛宝良. 一种计算结构时程响应的简单直接积分法[C]// 第23届全国结构工程学术会议. 兰州,2014.

[12] 牛宝良. 某离心机模型辨识与仿真[J]. 装备环境工程, 2015, 12(5): 61-66.

[13] 刘增光, 岳大灵, 安林超, 等. 基于MATLAB 的力反馈两级电液伺服阀建模与仿真[J]. 液压与气动, 2015(5): 83-85.

[14] 张宏, 高铭, 郭凯. 伺服阀开口度对电液伺服系统动态特性的影响[J]. 液压气动与密封, 2015(10): 27-30.

[15] 张军, 左哲清, 王书铭. 数字伺服阀卡滞问题研究[J]. 液压与气动, 2014(6): 105-107.

[16] 沈伟, 崔霞. 比例伺服阀静动态特性仿真建模[J]. 计算机仿真, 2015, 32(2): 236-240.

Dynamic Environment Test Equipment System Design Based on Simulating

NIU Bao-liang

(Institute of System Engineering, China Academy of Engineering Physics, Mianyang 621900, China)

ObjectiveTo introduce characteristics of simulation technology and its application in designing dynamic equipment system. Methods Development, characteristics and experience of simulation technology were introduced firstly. Application of Simulink software in dynamic equipment system was introduced with several examples. Results Main characteristic parameters concerned could be obtained quickly with Simulink simulation. It gave dependable data to evaluate or optimize the equipment system. Conclusion The computer simulation technology is quite mature and can be used in the dynamic environment test system design to advance the design level.

simulation; equipment; dynamic system; algebraic loops; environmental test

10.7643/ issn.1672-9242.2017.08.001

TJ01；TB114

A

1672-9242(2017)08-0001-10

2017-04-18；

2017-05-15

牛宝良 (1963—)，男，陕西人，硕士，研究员，主要从事振动、离心试验及相关设备研发。