区间痕迹下汽车事故再现结果不确定性问题的求解策略∗

邹铁方，李 华，赵 冬，李岳林，蔡 铭

区间痕迹下汽车事故再现结果不确定性问题的求解策略∗

邹铁方1，2，李 华1，2，赵 冬3，李岳林2，蔡 铭4

(1.长沙理工大学汽车与机械工程学院，长沙 410004； 2.湖南省工程车辆安全性设计与可靠性技术重点实验室，长沙 410004；3.公安部交通管理科学研究所，无锡 214151； 4.中山大学工学院，广东省智能交通系统重点实验室，广州 510275)

为更好地了解区间痕迹下事故再现结果不确定性分析问题的求解策略，在介绍常用不确定性分析方法后，基于分析和算例给出的求解建议，借助蒙特卡洛法探讨了车速大于事故路段限速值时概率的求解方法；且通过数值算例和真实案例等对相关方法进行了演示与验证。结果表明，不确定性分析方法可分为数值和理论分析两类，对于数值分析类，如对计算时间无要求可直接选用蒙特卡洛法，如对计算时间有要求则可选择遗传算法来满足需求；对于理论分析类，子区间技术是确保各方法所得结果逼近真值的有效方法。另外，若假定区间痕迹服从均匀分布，则可借助蒙特卡洛方法分析车速大于路段限速值的概率。

汽车事故再现；不确定性分析；区间；概率；子区间；遗传算法

前言

交通安全的改善和汽车安全性的设计，均需对道路交通事故进行深度调查[1]，以从中吸取教训和经验。通过对事故的深度调查，能获得大量的如碰撞角度、人体损伤和事故车速等数据，这些数据可为道路限速值设定[2]及相关汽车碰撞法规的制定提供依据。

事故再现是事故深度调查的重要组成，是获知事故车速等数据的核心依据，但由于人们认知的局限，往往导致事故再现结果包含不确定性。事故再现结果的不确定性通常由两部分原因所致，其一是事故再现模型的不确定性，主要引发因素是人们对客观世界认知的局限性[3]；其二是测量的不确定性，交通事故中，测量的不确定性主要指因事故现场痕迹受过往车辆、行人、雨、雪、尘等外界环境因素影响而慢慢消逝所导致的不确定性[4]。为提高依据事故深度调查所得数据的可靠性，进而确保据此而得的各类结论的可靠性，必须认真对待事故再现结果的不确定性问题。

因此，人们就此开展了大量深入的研究，并取得了丰硕成果。其一，在测量方面，卷尺、激光测距仪、摄影测量、三维扫描仪和无人机等技术均被应用于这一领域[5－7]，相关技术的引入和改进加快了事故现场测量的速度，并提高了测量精度，一定程度上降低了痕迹的不确定性。但如前所述，事故现场痕迹的不确定性主要来源是因受环境因素影响而导致的痕迹消逝，故仅从测量方面入手，无法根除痕迹的不确定性问题。其二，在模型方面，人们不仅研究了基于单一痕迹如人体损伤、车辆变形、事故现场洒落物和视频监控等的事故再现技术[8－11]，还用交叉验证和仿真等手段对不同痕迹所得结果进行验证[12－14]，确保事故再现结果的客观性。相关研究成果有效地降低了模型的不确定性，但并未涉及痕迹的不确定性问题。据此，第三方面的研究应运而生，即不确定性分析，人们借助相应的数学知识，研究从事故现场不确定痕迹所确定的空间域内寻找高可信度的事故再现结果取值区间或分布情况的不确定性分析技术，提出了不确定度理论、区间分析、上下界、差分法和响应曲面等方法[15－17]。

就事故再现而言，绝大多数情况下，仅能获得痕迹的取值范围，很难确切地知道痕迹的具体分布，因而可将痕迹视为仅包含区间信息的数[18]。故可认为事故再现结果不确定性分析的主要任务是在事故现场痕迹不确定取值区间所定义的空间域内寻找到事故再现结果的取值区间，相应引入很多求解策略，如区间理论[19]、泛灰理论[20]和改进的仿射算法[21]等。

据此，本文中首先简要介绍区间痕迹下已有事故再现结果取值区间的计算方法，并通过数值算例分析其特性；然后通过分析并引入优化和子区间等技术，给出区间痕迹下事故再现结果不确定性分析的求解建议；接着提出一种计算事故车辆车速大于事故路段限速值之概率的替代求解策略；最终给出一例真实案例对相关方法进行演示与验证。

1 事故再现结果取值区间计算方法

1.1 上下界法[16]

该方法通过组合区间痕迹的上下界后再计算模型结果，然后依据所有计算结果而获得相应模型的最大、最小值。对于一个有s区间痕迹的问题，相应的组合有2s种，自然需计算2s次。该方法的最大优势在于，当模型在定义域空间内单调时，能获得结果的真实取值区间。例如求模型

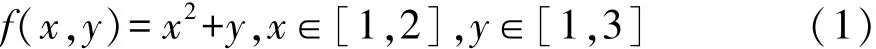
的取值区间，其真值为[2，7]。通过区间法而得的所有计算结果为{2，4，5，7}，则模型取值区间为[2，7]，显然与真值一致。但一旦模型不单调，则该方法所得结果会失真，比如求解下述模型的取值区间

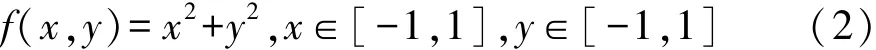
为求出模型f的取值区间，用上下界法算出的所有4个计算结果为{2，2，2，2}，则所得区间退化为一个数字2，显然与真实区间[0，2]相去甚远。

1.2 差分法[16]

差分法根据差分理论而来，它先获得各区间数的名义值，然后依据所有名义值计算1次模型结果，进而在其他名义值均不变的前提下，依次选择某个区间数的上、下界后再计算结果，最后根据所有计算结果而获得模型的最大和最小值。由此可知，对于一个有s区间痕迹的问题，相应的组合有2s＋1种，需计算2s＋1次。该方法是一种极为普通的方法，几乎所有情况都能算，但几乎所有情况下都算不出真值。例如模型(1)中，用该方法所得的所有计算结果为{4.25，3.25，5.25，3，6}，则由此可得f的取值区间为[3，6]；模型(2)中用该方法所得的所有计算结果为{0，1，1，1，1}，则由此可得f的取值区间为[0，1]，都能算出一个区间，但所得区间与真实区间均有差距。

1.3 区间理论法[19，22]

参照数学中的相关运算法则，提出了区间的相应运算法则，如加、减、乘、除等四则运算，进而可以依据模型表达式并通过相应的运算法则获得模型的取值区间。该方法因有固定的运算规则，虽然是一种非常简单的计算方法，但它的计算精度会随着模型中不确定参数出现次数的改变而改变，存在众所周知的区间扩张问题，例如计算模型

的取值区间，根据区间的四则运算法则，可得f的取值区间为[0.14，0.5]，与真值[0.17，0.4]有误差。但若式(3)的模型不变，仅将其表达式改为

则算得f的取值区间为[0.17，0.4]，与真值一致。

1.4 泛灰理论法[20]

该方法先将区间数转换为泛灰数，然后依据泛灰理论中提出的运算法则进行计算。该方法与区间法最大的相似之处在于均依据完善的运算法则进行计算，最大的不同之处在于采用泛灰理论计算时，只要模型给定，其结果不会像区间理论法那样随模型表达式的改变而改变。比如，用泛灰理论法计算模型(3)与模型(4)的取值区间，均为[0.25，0.29]，尽管它不是真值。不过泛灰理论有时也可能得到真值，例如计算模型(5)的取值区间

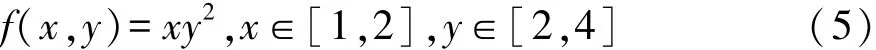
所得结果为[4，32]，与真值一致。

1.5 改进的仿射算法[21，23]

针对区间理论存在的区间扩张问题，学者引入了仿射理论，首先需将区间数表达为其仿射形式，然后依据仿射理论中的运算法则进行计算。为提高此类方法的精度，人们对该方法进行了改进，首先将模型表达成多项式的形式，然后将区间数表达为其仿射形式，进而可将模型转变为矩阵形式，最后求得结果的取值区间。与区间理论法、泛灰理论法类似，仿射算法有着完善的数学理论，且在某些情况下能算得与真值一致的结果，例如计算模型(2)的取值区间，可得[0，2]，与真值一致；但并非总是如此，例如用该方法所得模型(5)的取值区间为[－3.5，32]、模型(3)的取值区间为[0.14，0.41]，显然与各自的真值[4，32]和[0.17，0.4]皆有差距。

2 讨论分析

上述方法分为两大类，其一为数值类，包括上下界、差分法；其二为理论类，包括区间、泛灰理论和改进仿射法。数值类方法通过在模型定义域空间内取若干点后计算模型的结果，然后从所有结果中取极大、极小值作为模型的取值区间；而理论类方法则是参照已有的数学理论建立相对完善的理论体系，最明显的特征是各方法中均给出了各自的运算法则。

2.1 数值类方法

对于数值类方法而言，差分法毫无优势，而上下界法一旦遇到模型非单调的情况，则其所得结果便容易失真，要改善此类方法的计算精度，重点在于样本点的选择。一种是蒙特卡洛法，通过在模型定义域空间内随机生成若干样本点(一般需大于107个)，然后计算每个样本点对应的结果，进而获得模型的最大、最小值。只要样本数足够多，蒙特卡洛法所得结果必然会逼近真值。但蒙特卡洛法的缺点在于需要大量的样本点，因而需要耗费较多的计算时间，例如为计算模型

的取值区间，取107个样本点，在耗时0.550 848s后可得真值[－1，1]。为节约计算时间，可尝试减少样本点的个数，引入遗传算法，在种群40、最大遗传代数20、个体长度20、代沟0.95、交叉与变异概率分别为0.7与0.01的条件下，仅需0.046 4s，1 600个样本点即可获得模型的取值区间[－1，1]。可以看出，此例中蒙特卡洛法所需时间接近于遗传算法所需时间的12倍，这表明遗传算法确实能显著缩短计算时间，且其样本点会显著降低，样本点的分布情况见图1。

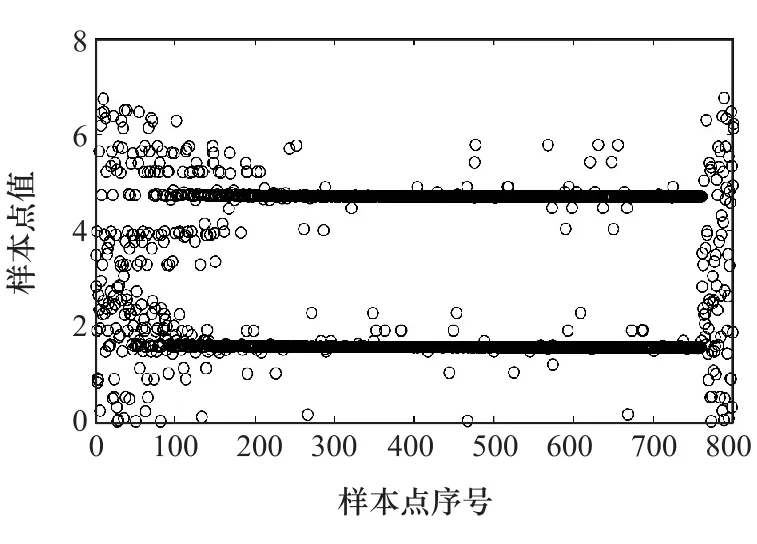
图1 遗传算法样本点

下面分别采用蒙特卡洛法与遗传算法计算模型(1)～模型(5)的取值区间，相应结果列入表1。表中MC表示蒙特卡洛法，GA表示遗传算法，tMC和tGA分别为两种算法的计算时间。因每次计算时间会有少许差异，故表中的时间为连续计算5次的平均时间。

表1 蒙特卡洛与遗传算法计算结果

由表1可知，用蒙特卡洛法与遗传算法均能获得非常接近于真值的计算结果，模型5中遗传算法结果还稍优于蒙特卡洛法；且遗传算法计算时间明显比蒙特卡洛法短。这表明对于数值类计算方法而言，为选用较少样本点就可快速找到模型的准确取值区间，优化是好的选择。除非事故鉴定人员对事故再现模型在某一空间域内的性质如单调性等非常了解，则可自主选择合理的数值类方法；否则，如对计算时间要求不高，可选择蒙特卡洛方法，因该方法几乎不需对问题的本质有任何了解且操作极其简单；但如对计算时间有要求，则需选择优化算法，比如遗传算法。

2.2 理论类方法

从理论上来说，如将不确定区间痕迹所定义的空间分成足够多的子空间，则与蒙特卡洛法类似，子空间往往会填充整个定义域空间，由此所得结果区间必然会逼近真值。

例如选用区间理论法计算模型(3)的取值区间，相关计算结果见表2。表中子区间数指某痕迹区间被分成子区间的数量；对于计算所得区间[a，b]及其真值[a0，b0]，误差为

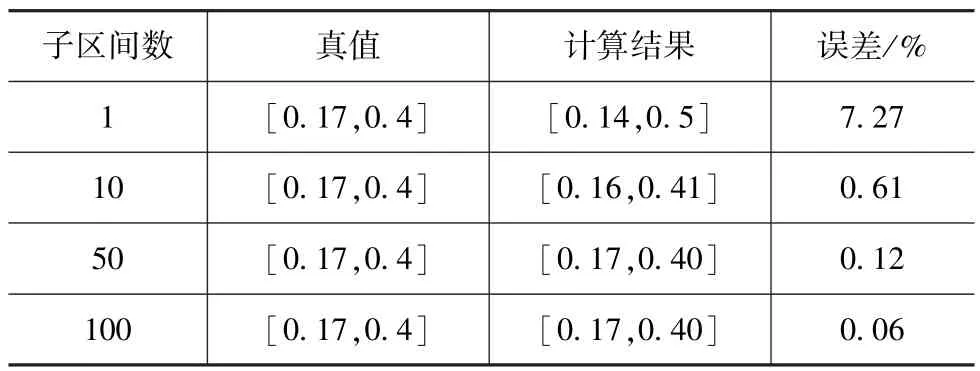
表2 区间理论法计算结果随子区间数量变化

由表2可见，随着子区间数的增加，误差越来越小，计算结果越来越趋于真值。

如选用泛灰理论法来计算模型(3)的取值区间，相关计算结果见表3。由表3可见，随着子区间数的增加，泛灰理论法所得值也逼近真值。

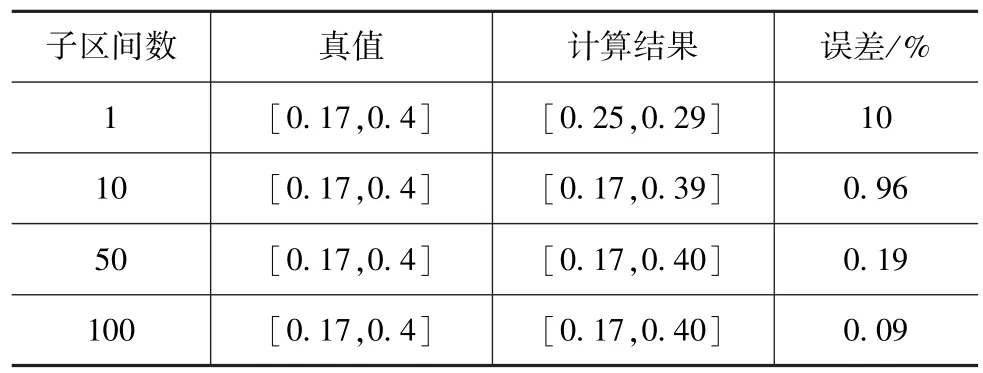
表3 泛灰理论法计算结果随子区间数量变化

选用改进的仿射算法相应的计算结果列于表4。由表4可见，随着子区间数的增多，改进仿射算法计算结果也趋于真值。

表4 改进仿射法计算结果随子区间数量变化

综合表2～表4可知，改进仿射算法的收敛速度最快，而泛灰理论法的收敛速度最慢，但这一结论是否具有普遍性，还需更多其他证明。不过有一点可以肯定，即随着子区间数的增加，各理论类方法所得模型区间均趋于真实区间。至于子区间数量的确定和子区间如何更好地组合、删除，以缩短计算时间，均可借鉴优化理论中的相关算法来实现，此处不再赘述。

3 区间痕迹下车速大于事故路段限速值的概率替代计算策略

对于事故再现而言，核心任务是找出事故车辆车速和碰撞发生位置，其中碰撞车速尤其重要。通过前面的分析可以看出，在区间痕迹下，选用数值类算法中的遗传算法或理论类方法中的子区间法，均能在区间痕迹所定义的空间内寻找到准确的模型取值区间。因此，自然可以得出事故车辆车速的准确取值区间，但这会产生另外一个问题，即如果所得车速区间恰好包含了事故路段的限速值，则会更关心

式中:v0为事故路段限速值；n0为n个计算所得车速中数值大于路段限速值的车速个数。下面通过一个具体案例来演示该方法。

2004年某日、某地，在一条同方向只有一条机动车道的城市道路上，一辆由西向东行驶的小客车在躲避一横穿公路的行人时撞到了该行人，导致该行人身受重伤和小客车内两名乘客受轻伤的交通事故。根据事故现场勘查，小客车前部有碰撞而导致的凹痕，行人与小客车的风窗玻璃发生了接触并导致风窗玻璃破裂，其中心位置距地面的高度为h＝[0.86，1.06]m，行人在事故中被抛出距离(行人抛距)为x＝[19.6，20.8]m；根据经验取人与地面间摩擦因数为μp＝[0.5，0.7]。已知事故路段限速为50km/h，现要求估算小客车与行人发生碰撞前瞬间的行驶速度。

该案例是一起典型车-人碰撞交通事故，可根据文献[24]的标准中汽车与行人碰撞且行人碰撞后被抛出的经验公式来计算事故车辆碰撞前的速度，即事故车速大于事故路段限速值的概率，而非仅仅关注某一车速取值区间。

这本身是一个矛盾的问题，痕迹是区间数，但车速要求给出概率信息，如不在原有区间痕迹条件下做出适当的假设，是不可能计算的。但现实生活中，这又是必须解决的问题，故而做出如下假设:如警方或其他事故调查机构给出某一痕迹的取值区间，则认为该痕迹在该区间内服从均匀分布。例如根据某一事故调查机构的调查，给出某事故中车辆的制动距离为[16，18]m，则认为在该事故中车辆的制动距离取区间[16，18]中的任意数值的概率均是相同的。如此则能借助蒙特卡洛方法轻松实现对该问题的求解。相应步骤如下:

(1)在每一痕迹区间内生成服从均匀分布的n个随机数，一般要求n不小于107；

(2)依据车速计算模型v＝g(X)(该模型可为已有公式或由仿真获得的回归模型)和步骤(1)中生成的样本，计算获得n个相对应的车速；

(3)对计算所得n个车速进行统计分析。事故车辆车速大于路段限速值的概率为

因模型表达式相对较为简单，故先选择数值类算法中的蒙特卡洛法获得事故车辆车速取值区间，为[42.4，51.3]km/h，该区间正好包含了路段限速值，进而借助上述方法可知车速大于事故路段限速值的概率为p(v＞50)＝3.9%。类似的不确定性分析结果在一定程度上满足了人们的现实需求，也更好地解释了不确定痕迹，能显著提高车速再现结果的说服力。

4 仿真案例分析

下面通过一个案例来演示仿真结果不确定性分析问题的求解策略。

2014年5月的某天上午，天气晴，在我国某省，一辆自西向东行驶的小轿车和一辆自西向北转弯行驶的两轮电动车发生碰撞，造成了两轮电动车驾驶员死亡的重大交通事故。事故现场为干燥沥青路面，其摩擦因数为μp，根据GA/T 643—2006《典型交通事故形态车辆行驶速度技术鉴定》，μp的取值区间为[0.6，0.8]；在事故现场采集到了小轿车的制动距离s为[20.3，23.8]m。图2给出事故现场示意图。根据警方的委托，需要对这起事故中小轿车的车速进行估算。

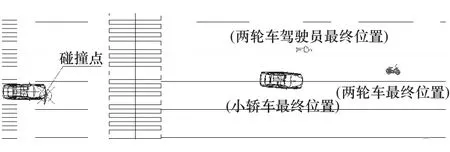
图2 事故现场示意图

因模型为仿真模型，无法采用诸如蒙特卡洛之类的数值类方法，故须先找出仿真模型的近似响应面模型。故先借助拉丁方实验设计在区间痕迹所定义的空间域内生成12个样本点，见表5，然后借助Pc-Crash进行仿真实验。

在仿真过程中，要求每一次再现中均保证事故现场痕迹可在仿真中得到合理解释。如进行第5次实验，需要反复调整车辆的车速及其他相关参数，以使仿真中痕迹与事故现场痕迹相吻合。图3给出两轮车变形情况对比。可以发现，两轮车的最大变形位置和仿真中碰撞位置是吻合的，这说明两轮车与小轿车的接触位置与实际情况相符。图4给出两轮车驾驶员头部与小轿车风窗玻璃接触位置。由图可见，小轿车风窗玻璃凹陷破碎的地方和仿真中被撞人员头部接触位置一致，这说明人-车接触位置与实际情况相符。图5为二维仿真结果。由图5可知，两轮车驾驶员、两轮电动车和小轿车的最终位置与事故现场图能吻合很好，说明仿真结果符合实际情况。相应的实验结果(事故车辆车速)见表5。

表5 实验设计和仿真结果

图3 小轿车与两轮车碰撞时的相对位置

图4 两轮车驾驶员头部与小轿车风窗玻璃接触位置

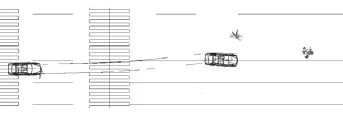
图5 二维仿真结果

依据表5中的数据，通过回归分析，可得近似响应面模型为

该回归方程的相关系数为0.997、残差平方和为0.11，表明回归关系显著。然后借助遗传算法，获得车速的取值区间，为[75.9，86.7]km/h。如事故路段限速60km/h，很明显该区间不包含路段限速值，可就此结束不确定性分析过程；但如事故路段限速80km/h，则需借助第3节的方法分析车速大于80km/h的概率，通过分析可得p(v＞80)＝52.36%。相关研究结果对于更好地解释事故现场痕迹会有所帮助，可提升车速再现结果的说服力。

5 结论

首先介绍常用区间痕迹下事故再现结果取值计算方法，再通过分析指出，优化和子区间是获取精确取值区间的最佳途径，并用相关的案例对各结论进行了验证与演示，得到如下结论。

(1)区间痕迹下，事故再现结果取值区间计算方法可分为两类，其一为数值类方法，包括上下界、差分、蒙特卡洛及遗传算法；其二为理论类方法，包括区间、泛灰理论法和改进仿射算法等。对于数值类方法，为获得精确的模型取值区间，可通过大量增加样本点数据，如蒙特卡洛方法；或借助遗传优化算法，以较短时间和较少样本寻找到模型的取值区间。对于理论类方法，为保证在任何情况下均可获得准确的模型取值区间，子区间是好的解决办法。数值算例显示，随着子区间数的增加，所有方法的计算结果均逼近真实区间。

(2)算例显示，随着子区间数的增加，改进仿射算法的收敛速度最快，区间理论法次之，而泛灰理论法最慢。但该结论是否具有普遍意义，尚需更多证明。

(3)如计算所得车速取值区间包含了事故路段限速值，则假设区间痕迹服从均匀分布，然后可以借助蒙特卡洛方法分析车速大于路段限速值的概率。

(4)引入子区间技术，可提升不确定性分析中理论类方法的精度，但当不确定痕迹和子区间数均较多时，须组合大量的子空间域，这会导致计算时间大量增加，因此需要今后进一步深入研究，如借助优化理论中的相关算法以更快地找到目标子空间域，进而获得准确的取值区间。

[1] 李伟楠，王雪松.基于事故深度调查的城市交通事故特征分析[J].中国安全科学学报，2012，22(12):89－95.

[2] 聂进，吴京梅，吴玲涛，等.基于行人和自行车交通安全的城市道路限速值研究[J].中国公路学报，2014，27(7):91－97.

[3] Wojciech Wach.Calculation reliability in vehicle accident reconstruction[J].Forensic Science International，2016，263:27－38.

[4] ZOU Tiefang，HU Lin，LI Pingfan，et al.A simple algorithm for analyzing uncertainty of accident reconstruction results[J].Forensic Science International，2015，257:229－235.

[5] Brach Raymond M，Brach R Matthew.Vehicle accident analysis and reconstruction methods[M].SAE International Publisher，Pennsylvania，USA，2005.

[6] 王丰元，宇仁德，杜守旭.道路交通事故现场摄影测量原理与模型试验[J].中国公路学报，2001，14(1):100－103.

[7] 杨博，金先龙，张晓云，等.基于数字化摄影测量的交通事故信息采集和过程再现[J].汽车工程，2010，32(6):530－534.

[8] PENG Yong，YANG Jikuang，DECK Caroline，et al.Finite element modeling of crash test behavior of windshield laminated glass [J].International Journal of Impact Engineering，2013，57:27－35. [9] XU Jun，LI Yibing，LU Guangquan，et al.Reconstruction model of vehicle impact speed in pedestrian-vehicle accident[J].International Journal of Impact Engineering，2009，36:783－788.

[10] 许洪国，任有，王利芳，等.硬路面碎块抛物运动模型[J].交通运输工程学报，2002，2(3):63－67.

[11] WONG T W，TAO C H，CHENG Y K，et al.Application of cross-ratio in traffic accident reconstruction[J].Forensic Science International，2014，235:19－23.

[12] DAVIS G A.A Bayesian approach to cross-validation in pedestrian accident reconstruction[J].SAE International Journal of Passenger Cars-Mechanical Systems，2011，4(1):293－303.

[13] 邹铁方，余志，蔡铭，等.基于Pc-Crash的车-人事故再现[J].振动与冲击，2011，30(3):215－219.

[14] WEI Lang，GONG Biao，CHEN Tao.Vehicle continuous collision accident reconstruction system development[J].Procedia-Social and Behavioral Sciences，2013，96:1659－1669.

[15] 袁泉，李一兵.车辆交通事故再现能量方法的不确定度评定[J].中国公路学报，2002，15(1):110－112.

[16] ZOU Tiefang，CAI Ming，DU Ronghua，et al.Analyzing the uncertainty of simulation results in accident reconstruction with response surface methodology[J].Forensic Science International，2012，216(1－3):49－60.

[17] ZHANG Xiaoyun，HU Zhen，DU Xiaoping.Probabilistic inverse simulation and its application in vehicle accident reconstruction [J].ASME Journal of Mechanical Design，2013，135(12): 12100601－12100610.

[18] Wojciech Wach，Jan Unarski.Uncertainty of calculation results in vehicle collision analysis[J].Forensic Science International，2007，167(2－3):181－188.

[19] ZOU Tiefang，YU Zhi，CAI Ming，et al.Two non-probabilistic methods for uncertainty analysis in accident reconstruction[J]. Forensic Science International，2010，198:134－137.

[20] WANG Qinyin.Foundation of grey mathematics[M].Wuhan: Huazhong University of Science＆Technology Press，1996.

[21] DEGRAUWE D，LOMBAERT G，DE ROECK G.Improving interval analysis in finite element calculations by means of affine arithmetic[J].Computers＆Structures，2010，88(3－4):247－254.

[22] ZOU Tiefang，CAI Ming，SHU Xiong.Response surface methodology and improved interval analysis method-For analyzing uncertainty in accident reconstruction[J].Forensic Science International，2012，222(1－3):306－312.

[23] SHOU Huahao，LIN Hongwei，MARTIN Ralph，et al.Modified affine arithmetic is more accurate than centered interval arithmetic or affine arithmetic[C].Mathematics of Surfaces－10th IMA International Conference，Berlin:Springer Berlin Heidelberg，2003: 355－365.

[24] GA/T 643—2006典型交通事故形态车辆行驶速度技术鉴定[S].北京:中国标准出版社，2006.

Solving Strategies for Reconstruction Results Uncertainty Issues of Accidents with Interval Traces

Zou Tiefang1，2，Li Hua1，2，Zhao Dong3，Li Yuelin2＆Cai Ming4
1.School of Automobile and Mechanical Engineering，Changsha University of Science and Technology，Changsha 410004；2.Key Laboratory of Safety Design and Reliability Technology for Engineering Vehicle，Hunan Province，Changsha 410004；3.Traffic Management Research Institute of Ministry of Public Security，Wuxi 214151；4.School of Engineering，Sun Yat-sen University，Guangdong Provincial Key Laboratory of Intelligent Transportation System，Guangzhou 510275

In order to better understand the solving strategy of uncertainty analysis of reconstruction results in traffic accidents with interval traces，existing uncertainty analysis methods are presented firstly，then some solving suggestions are proposed based on above analysis and some calculation examples.The solving methods of the probability of reconstructed speed greater than speed limit are explored with Monte Carlo method and related methods are demonstrated/validated by calculation examples and real accident cases.Results show that uncertainty analysis methods can be classified into two types:numerical analysis and theoretical analysis.For numerical analysis，Monte Carlo method can be directly used if calculation time is not restricted；otherwise，genetic optimization algorithm is recommended.As for theoretical analysis，sub-interval technique is an effective method for ensuring the result approaching true values.In addition，if assuming interval traces follow uniform distribution，then the probability of reconstructed speed greater than speed limit can be found by Monte Carlo method.

vehicle accident reconstruction；uncertainty analysis；interval；probability；sub-interval；genetic algorithm

10.19562/j.chinasae.qcgc.2017.08.008

∗国家自然科学基金(51775056)、广东省科技计划项目(2015B010110005)和道路交通安全公安部重点实验室开放基金(2016ZDSYSKFKT08)资助。

原稿收到日期为2016年8月5日，修改稿收到日期为2016年10月24日。

赵冬，硕士研究生，E-mail:tmrizd＠163.com。