基于Monte-Carlo随机有限元法的地下筒仓可靠性灵敏度研究

陈桂香，崔晨星，付志永，蒋敏敏

（河南工业大学 土木建筑学院，河南 郑州 450001）

基于Monte-Carlo随机有限元法的地下筒仓可靠性灵敏度研究

陈桂香，崔晨星，付志永，蒋敏敏

（河南工业大学 土木建筑学院，河南 郑州 450001）

岩土体环境、结构、材料等因素对地下钢筋混凝土筒仓结构失效产生影响。通过随机有限元法，建立了地下筒仓可靠性灵敏度分析模型，分析随机参数对功能函数的灵敏度和相关性。研究表明：筒仓半径是影响仓壁混凝土强度失效的主要因素，相关性系数为-86.5%，半径越大对强度影响越不利；钢筋弹性模量是影响仓壁裂缝失效的主要因素，相关性系数为79.5%，钢筋弹性模量越大对仓壁裂缝控制越有利；混凝土弹性模量是仓顶梁板结构挠曲失效的主要因素，相关性系数为97.0%，混凝土弹性模量的增大对仓顶梁板挠度控制较有效；混凝土弹性模量、筒仓半径是仓壁结构变形失效的主要因素，相关性系数分别为68.7%和-67.6%，混凝土弹性模量和筒仓半径增大，对仓壁结构变形控制分别产生有利和不利影响。

地下筒仓；随机有限元；灵敏度；相关性分析

0 引言

地上粮仓在环境温度偏高时，常常发生储粮品质劣变和生虫等问题。地下大直径钢筋混凝土筒仓是一种新型的地下储粮结构，具有准低温环境储粮、节地、节能和绿色环保等优点。由于地下仓仓体处在复杂的岩土体和地下水环境中，环境、结构、材料等因素对仓体结构失效均会产生影响，而各因素对可靠性的影响程度则有待确定[1-4]。

目前对于地下大直径钢筋混凝土筒仓的研究，主要采用数值模拟等方法对结构受力机理和优化设计进行研究。涂成顺[5]采用初参数法和有限元法研究了中间带有柱子支撑的地下筒仓仓壁的内力和位移，并将两种方法计算结果进行对比分析；熊晓莉等[6]根据地下试验仓现场监测结果，分析了仓壁土压力的取值方法，并通过圆柱壳模型分析法和有限元分析法研究了地下筒仓仓壁结构受力特性；熊晓莉等[7]采用下端固定、上端简支圆柱壳模型，研究了仓壁竖向弯矩和环向力分布规律及仓壁承载特性等。贾腾南[8]在空间受力条件下对地下筒仓仓壁进行有限元分析，并对试验仓仓壁进行现场监测分析。

Monte-Carlo法抽样次数趋于无穷时可得到结构可靠性分析的精确解。本文采用有限元程序ANSYS中的Monte-Carlo概率设计法，对地下筒仓进行可靠性分析，得出地下筒仓中各随机变量对仓体结构失效概率的灵敏度和随机变量的相关性系数。通过分析随机参数的灵敏度，找出对目标失效概率影响较大的参数，分析随机参数的相关系数，得出随机参数对目标失效概率的相关性。

1 Monte-Carlo法灵敏度基本原理

Monte-Carlo可靠性分析方法是通过随机模拟或统计试验进行结构可靠性分析。Monte-Carlo法求解失效概率Pf，由基本随机变量的联合概率密度函数fX（x）产生N个随机变量的随机样本xj（j=1，…，N），将这 N 个随机样本代入功能函数 g（x），落入失效域 F=｛x∶g（x）≤0｝的样本点数为 Nf，则失效概率Pf的估计值为：

可靠性灵敏度为失效概率Pf对基本随机变量xi的分布参数的偏导数，其中mi为第i个变量的分布参数的总数，即：

将式（2）变换成数学期望的表达形式：

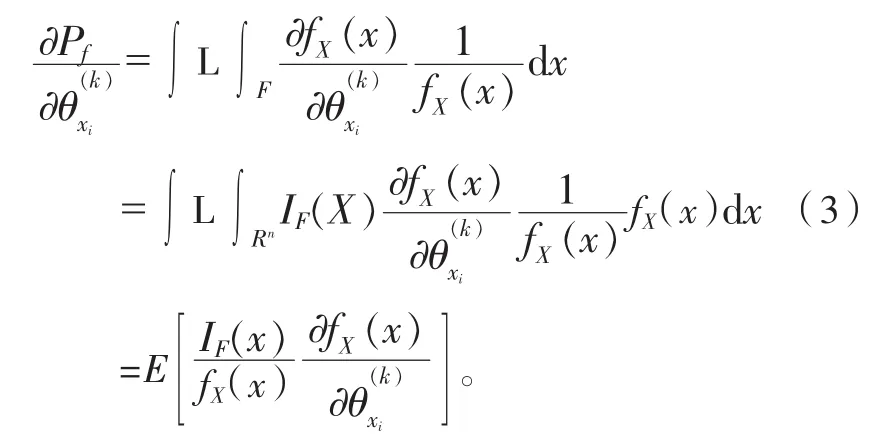
Monte-Carlo法数值模拟，以样本均值代替总体均值，则数学期望形式表示可靠性的灵敏度，可由样本函数的平均值估计：

式中：xi是按联合密度函数fX（x）抽取的N个样本中的第j个样本。

2 地下筒仓可靠性灵敏度分析模型的建立

2.1 有限元模型

以郑州地区新建的地下大直径钢筋混凝土试验筒仓为研究对象，该筒仓内径25 m，仓壁高15 m，仓壁厚度0.35 m，仓顶埋置深度2 m。

场地主要土层的组成及物理、力学指标如表1所示。根据土层参数计算仓顶上部覆土荷载为40 kPa。仓壁为圆筒形结构，由于其空间拱效应，变形很小，仓壁外侧土压力接近于静止土压力，按静止土压力计算。静止土压力系数为Ki=1-sinφi，黏性土按水土合算法，砂土和粉土按水土分算法计算。仓壁上地下水土侧压力总分布见图1。

表1 场地主要土层的组成及指标Table 1 Composition and index of main soil layer

图1 地下水土侧压力总分布Fig.1 The lateral pressure total distribution graph of underground soil&water

仓壁材料为钢筋混凝土，混凝土标号为C40，弹性模量 E=3.25×107kN/m2，泊松比 μ=0.2。筒仓仓壁及倒锥形仓底属壳体，选取SHELL181单元建立仓壁有限元模型，将仓壁沿纵向等分为50段，沿环向等分为80段，划分为四边形单元。在模型仓顶施加40 kPa的覆土荷载，仓壁施加图1所示的地下水土侧压力，在地下筒仓底面施加3个方向位移约束DOF=0。几何模型及网格划分见图2。

2.2 基本随机变量及统计信息

本研究的随机有限元分析中，影响地下大直径钢筋混凝土筒仓可靠性的材料特性和场地土的随机变量以及各随机变量的分布特征如表2、表3所示[9-10]。

2.3 功能函数的建立

（1）仓壁混凝土强度功能函数。在仓壁混凝土强度的可靠性分析中，采用Hsich-Ting-Chen四参数强度准则建立功能函数[11]：

图2 地下大直径钢筋混凝土筒仓模型Fig.2 Large diameter reinforced concrete underground silo model

表2 材料特性的变量统计特征Table 2 Variable statistical characteristics of material properties

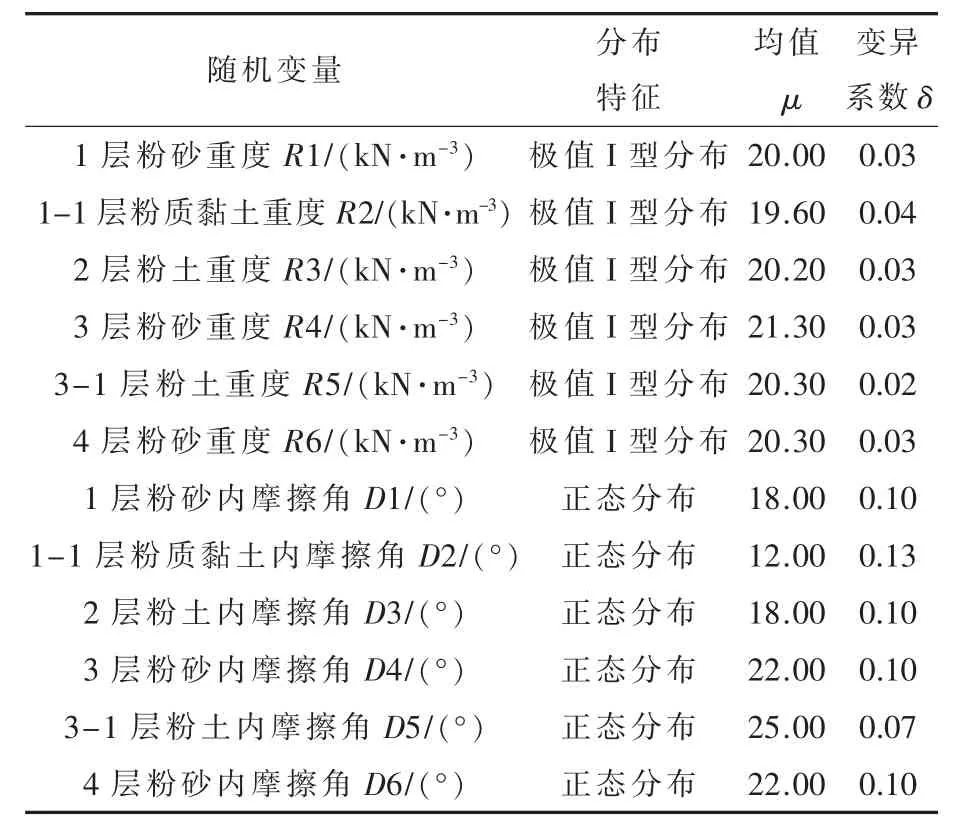
表3 场地土的随机变量统计特征Table 3 Statistical characteristics of random variables in soil

式中：σ1、σ2、σ3分别为第 1、第 2、第 3 主应力，fc表示混凝土的轴心抗压强度。

（2）仓壁裂缝功能函数。建筑结构按所处环境类别和结构类型的不同应分别对裂缝的宽度进行控制。对于允许出现裂缝的构件，构件的最大裂缝宽度采用《混凝土结构设计规范》方法（规范法）计算。地下筒仓结构位于地下干湿交替的环境中，设计环境类别为二b，仓壁裂缝控制等级为三级，地下筒仓仓壁最大裂缝宽度的限值取0.2 mm，仓壁裂缝控制的功能函数为：

（3）仓顶梁板结构挠度功能函数。地下大直径钢筋混凝土筒仓仓顶梁板为受弯构件，最大挠度计算值不超过规范法的限值。仓顶梁板结构挠度控制的功能函数为：

（4）仓壁结构变形功能函数。地下筒仓仓壁结构的变形过大会导致筒仓使用功能的失效。研究表明地下大直径钢筋混凝土筒仓仓壁的径向最大位移为12 mm[12]。仓壁结构变形控制的功能函数为：

3 计算结果分析

基于ANSYS的概率设计，通过Monte-Carlo法抽样106次，得出仓壁混凝土强度、仓壁裂缝、仓顶梁板结构挠度、仓壁结构变形各功能函数的失效概率分 别 为 Pf1=3.998×10-4、Pf2=1.203×10-4、Pf3=2.907×10-4、Pf4=5.974×10-4。

3.1 随机参数的灵敏度分析

Monte-Carlo随机有限元可靠性分析得出的各失效模式下，失效概率关于各随机参数灵敏度的计算结果如图3—图6所示。

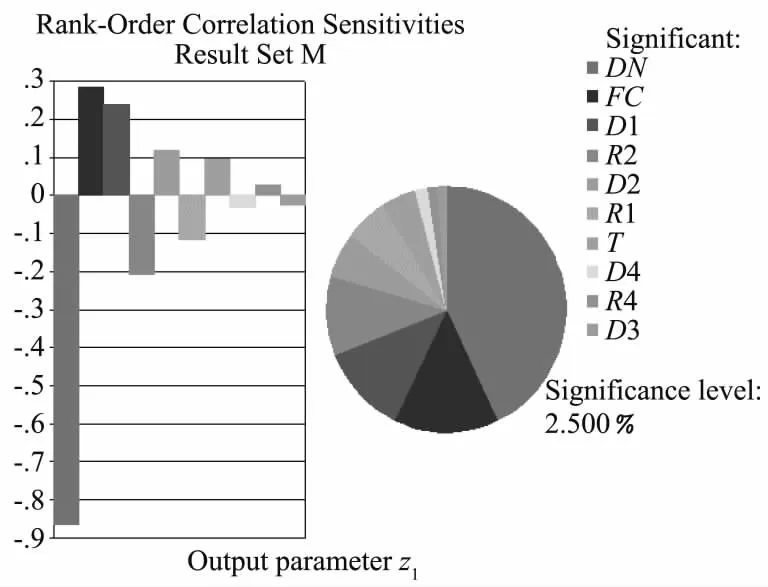
图3 仓壁混凝土强度可靠性灵敏度分布Fig.3 Distribution of reliability sensitivity of concrete strength of silo wall

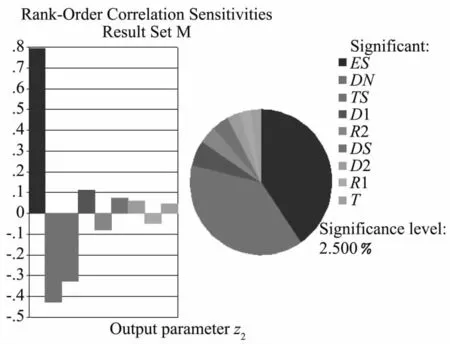
图4 仓壁裂缝可靠性灵敏度分布Fig.4 Distribution of reliability sensitivity of silo wall cracks

图5 仓顶梁板结构挠度可靠性灵敏度分布Fig.5 Distribution of reliability sensitivity of structural deflection of silo beam and plate

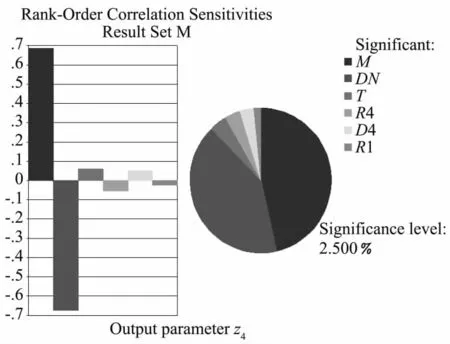
图6 仓壁结构变形可靠性灵敏度分布Fig.6 The distribution of reliability sensitivity of structural deformation of silo wall

由图3可知，对仓壁混凝土强度失效概率影响最大的参数为筒仓半径DN，此外混凝土抗压强度FC、仓壁厚度T、1层粉砂内摩擦角D1和重度R1、1-1层粉质黏土内摩擦角D2和重度R2、2层粉土内摩擦角D3以及3层粉砂内摩擦角D4和重度R4共9个随机参数的灵敏度大于2.5%，对仓壁混凝土强度的失效概率影响较大。

由图4可知，对仓壁裂缝失效概率影响最大的参数为钢筋弹性模量ES，此外筒仓半径DN、钢筋保护层厚度TS、钢筋直径DS、仓壁厚度T、1层粉砂内摩擦角D1和重度R1以及1-1层粉质黏土内摩擦角D2和重度R2共8个随机参数的灵敏度大于2.5%，对仓壁裂缝的失效概率影响较大。

由图5可知，对仓顶梁板结构挠度失效概率影响最大的参数为混凝土弹性模量EC，此外仓壁厚度T、筒仓半径DN以及1层粉砂内摩擦角D1共3个随机参数的灵敏度超过了2.5%，对仓顶梁板结构挠度的失效概率影响较大。

由图6可知，对仓壁结构变形失效概率影响最大的参数为混凝土弹性模量EC和筒仓半径DN，此外仓壁厚度T、1层粉砂重度R1以及3层粉砂内摩擦角D4和重度R4共4个随机参数的灵敏度超过了2.5%，对仓壁结构变形的失效概率影响较大。

3.2 随机参数的相关性分析

上述参数灵敏度分析，说明了随机参数对失效概率的影响程度。本研究更进一步通过ANSYS可靠性分析，处理得出各主要影响的随机参数与功能函数 z1、z2、z3、z4的相关性系数如表 4 所示。

表4 主要输入随机参数与各功能函数的相关性系数Table 4 The correlation coefficient between the main input random parameters and each performance function%

相关性分析结果中，相关性系数为正值，表示这些参数中的某一个参数增大、其他参数不变的情况下，所对应的功能函数随之增大，表明功能函数的失效概率降低，可靠指标变大，对可靠性越有利；相关性系数为负值，表示这些参数中的某一个参数增大、其他参数不变的情况下，所对应的功能函数的失效概率就会变高，可靠指标相应变小，则对可靠性越不利；表中的数值0表示该输入随机参数对控制条件可靠性的灵敏度小于2.5%，对功能函数的影响可以忽略。

从相关性分析结果可见，筒仓半径DN与仓壁混凝土强度破坏功能函数的相关性系数最大，为-86.5%，表明筒仓半径对仓壁混凝土强度破坏影响最大，且半径越大对强度影响越不利。钢筋弹性模量ES与仓壁裂缝控制下的功能函数的相关性系数最大，为79.5%，钢筋弹性模量越大对仓壁裂缝控制越有利。混凝土弹性模量EC与仓顶梁板挠度控制下的功能函数的相关性系数最大，为97.0%，混凝土弹性模量的增大对仓顶梁板挠度控制较有效。混凝土弹性模量EC和筒仓半径DN与仓壁结构变形控制下的功能函数的相关性系数最大，分别为68.7%和-67.6%，表明混凝土弹性模量和筒仓半径的增大，分别对仓壁结构变形控制为有利和不利。

4 结论

通过ANSYS中的可靠性分析Monte-Carlo法建立了地下筒仓可靠性灵敏度分析模型，对郑州地下大直径钢筋混凝土试验筒仓进行了可靠性有限元数值模拟，分析各控制条件的功能函数和各个随机参数的灵敏度以及相关性系数，得出以下结论：

（1）通过随机参数灵敏度分析，在筒仓结构分析的仓壁混凝土强度破环、仓壁裂缝、仓顶梁板结构挠度、仓壁结构变形等功能要求上，筒仓半径对仓壁混凝土强度失效影响最大，钢筋弹性模量对仓壁裂缝失效概率影响最大，混凝土弹性模量对仓顶梁板结构挠度影响最大，混凝土弹性模量和筒仓半径对仓壁结构变形失效影响最大。

（2）随机参数与地下筒仓功能性要求的相关性分析表明，筒仓半径与仓壁混凝土强度破坏影响的相关性系数为-86.5%，表明半径越大对强度影响越不利；钢筋弹性模量与仓壁裂缝影响的相关性系数为79.5%，表明钢筋弹性模量越大对仓壁裂缝控制越有利；混凝土弹性模量与仓顶梁板挠度影响的相关性系数为97.0%，表明混凝土弹性模量的增大对仓顶梁板挠度控制较有效；混凝土弹性模量、筒仓半径与仓壁结构变形的相关性系数为68.7%和-67.6%，分别表明混凝土弹性模量和筒仓半径的增大，对仓壁结构变形控制为有利和不利。

［1］ AU S K.Reliability-based design sensitivity by efficient simulation ［J］.Computers&Structures， 2005， 83（14）:1048-1061.

［2］ XIAO N C， HUANG H Z， WANG Z， et al.Reliability sensitivity analysis for structural systems in interval probability form［J］.Structural and MultidisciplinaryOptimization， 2011，44（5）:691-705.

［3］ 刘言凤.钢筋混凝土梁可靠度的灵敏度分析［D］.哈尔滨:哈尔滨工业大学，2007.

［4］ 蒋伟，吕大刚.钢管混凝土拱面外稳定的可靠度与灵敏度分析［J］.哈尔滨工业大学学报， 2012， 44（12）:8-12.

［5］ 涂成顺.地下大直径钢筋混凝土筒仓仓壁结构分析及比较［D］.郑州:河南工业大学，2011.

［6］ 熊晓莉，金立兵，王振清.钢筋混凝土地下粮仓仓壁土压力取值方法及仓壁结构受力分析［J］.应用基础与工程科学学报，2016，24（1）:103-114.

［7］ 熊晓莉，金立兵，史笑珂，等.钢筋混凝土圆形地下粮仓仓壁承载力计算方法研究［J］.河南工业大学学报（自然科学版），2015，36（1）:95-99.

［8］ 贾腾南.基于空间受力的地下钢筋混凝土粮食筒仓仓壁受力分析［D］.郑州:河南工业大学，2014.

［9］ 张璐璐，张洁，徐耀，等.岩土工程可靠度理论［M］.上海：同济大学出版社，2011.

［10］ 李典庆，蒋水华，周创兵.基于非侵入式随机有限元法的地下洞室可靠度分析［J］.岩土工程学报， 2012，34（1）:123-129.

［11］ 李红梅，李树山，解伟.基于Hsich-Ting-Chen混凝土强度准则的可靠度判据研究［J］.华北水利水电学院学报，2011，32（5）:63-65.

［12］ 李刚，许林，程耿东.基于ANSYS软件的大型复杂结构可靠度分析［J］.建筑结构，2002， 32（5）:58-61.

RELIABILITY SENSITIVITY ANALYSIS OF UNDERGROUND SILO BASED ON MONTE-CARLO STOCHASTIC FINITE ELEMENT METHOD

CHEN Guixiang，CUI Chenxing，FU Zhiyong，JIANG Minmin
（School of Civil Engineering and Architecture， Henan University of Technology， Zhengzhou 450001， China）

Rock and soilenvironment， structure and materialare factorsaffecting structure failure of underground concrete silo.A reliability sensitivity analysis model was established to study sensitivity and correlation between random parameter and performance function based on stochastic finite element method.Research showed that， silo radius was a major factor affecting strength failure of concrete silo wall， with correlation coefficient of-86.5%，which indicated that the increase of radius had adverse effects on the strength.Steel bar elastic modulus is a key factor affecting crack failure of silo wall，with correlation coefficient of 97%，which indicated that the increase of elastic modulus had positive effects on crack control.Concrete elastic modulus is a decisive factor affects flexure failure of beam and plate on concrete silo roof，with correlation coefficient of 97%，which indicated that the increase of elastic modulus was more effective in controlling deflection of beam and plate on silo roof.Concrete elastic modulus and silo radius were influential factors affecting deformation failure of concrete silo wall，with correlation coefficients of 68.7%and-67.6%respectively，which indicated that the increases of concrete elastic modulus and silo radius had positive and adverse influences on deformation control of silo wall，respectively.

underground silo；stochastic finite element；sensitivity；correlation analysis

TU91

：A

1673-2383(2017)04-0086-05

http://kns.cnki.net/kcms/detail/41.1378.N.20170828.0857.032.html

网络出版时间：2017-8-28 8:57:24

2016-09-09

国家粮食局公益性行业科研专项（2015449001、201513001）；国家自然科学基金项目（51408197）

陈桂香（1976—），女，山西吉县人，博士，教授，主要从事结构设计优化和工程风险管理等方面研究。