利用思维导图设计二次函数复习课

彭高阳

摘要：二次函数是初中数学数与代数课程领域的重要内容，它是客观地反映现实世界中变量之间的数量关系和变化规律的一种非常重要的数学模型，它承载着数形结合、分类讨论、化归与转化等数学思想的应用.思维导图是一种表达发射性思维的有效的图形思维工具，它运用图文并重的技巧，把主题关键词与图像、颜色等建立记忆链接，从而开启人类大脑的无限潜能.本节课从一道中考题入手，利用波利亚怎样解题表，融入思维导图，提高课堂效率.

关键词：二次函数思维导图 教学设计

一、教材分析

1.地位和作用

函数是初等数学最基本的概念之一，贯穿于整个初等数学教学的体系之中，它是数学建模的重要工具.二次函数是初中数学数与代数课程领域的重要内容，它是客观地反映现实世界中变量之间的数量关系和变化规律的一种非常重要的数学模型，承载着数形结合、分类讨论、化归与转化等数学思想的应用.二次函数是中考压轴题的必考内容.

2.学情分析

（1）通过本章的学习，学生基本掌握二次函数的定义、图象、性质等相关知识.

（2）学生的分析、理解能力有提高.能利用数形结合和化归的数学思想，独立思考或合作探究来解决一些实际问题.

（3）学生学习能力有差异，两极分化明显.

二、教学目标

1.知识目标

通过对实际问题情境分析确定二次函数表达式的过程，会根据公式确定图像的顶点、开口方向和对称轴（公式不要求记忆和推导） ，体会二次函数的意义.

2.能力目标

（1）会用描点法画出二次函数的图像，能从图像上认识二次函数的性质，并能解决简单的实际问题.

（2）会利用二次函数的图像求一元二次方程的近似值.

（3）学生通过知识的学习，掌握类比、转化等数学学习方法，形成自主探索与合作探究的学习习惯.

3.情感目标

在教学中渗透美的教育，渗透数形结合和化归的数学思想，让学生在教学活动中，体会探索与创新，与同学分享成功的喜悦.

三、教学重点难点

（1）本节课教学重点二次函数常见压轴题型的归纳.

（2）从图形中发现问题，构建数学模型来解决问题.

四、教法学法

教无定法，贵在得法.本节课本节课从一道中考题下手，创设有助于学生探索思考的问题情境，引导学生积极思考探索，让学生经历“观察、发现、归纳”的过程，发挥学生学习的主动性.再引入变式教学，让学生借助波利亚怎样解题表，融入思维导图，优化解题，使学生思想方法得到提升.同时借助多媒体课件、投影仪教学，提高课堂效率.

五、教学过程

（一）自主复习

1.广东省省卷近六年中考统计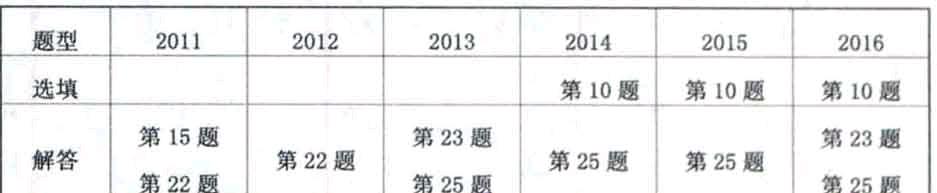

2.二次函数思维导图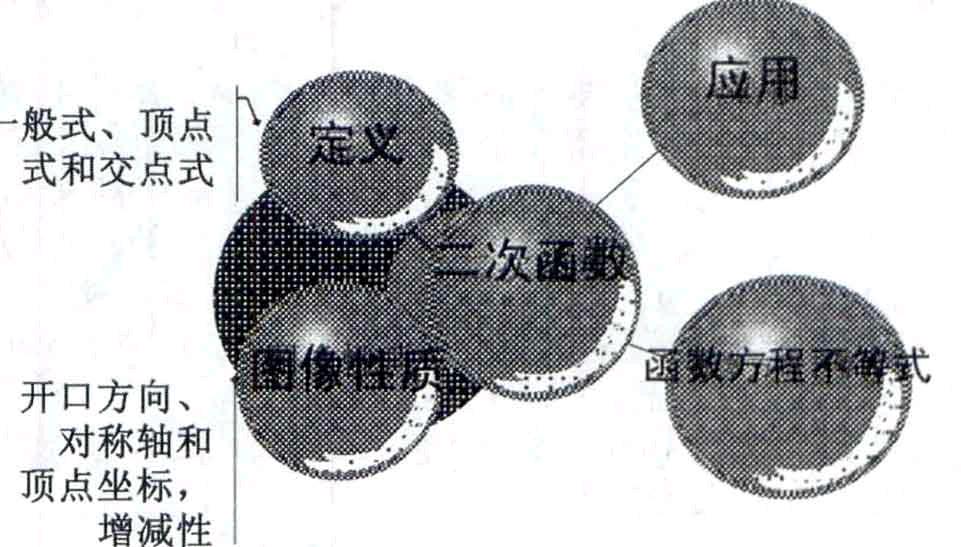

学生活动：学生展示动手制作思维导图，并讲解讨论.

设计意图：思维导图有助于二次函数的关键词在学生脑海里加深印象，有助于理解知识的收集、整理和归纳的过程，更有助于知识的系统化和条理化.

老师点评：思维导图是运用图文并重的技巧，把主题关键词与图像、颜色等建立记忆链接，从而开启人类大脑的无限潜能.

（二）交流合作探究

如图，抛物线y=-x2+bx+c与x轴交与A（1，0），B（-3，0）两点，顶点为D，交y轴于C.

（1）求该抛物线的解析式与△ABC的面积.

学生活动：学生展示.

设计意图：上一题二次函数开口向上，此题开口向下，便于学生对比.

老师点评：利用待定系数法求二次函数解析式，有一般式、頂点式和交点式三种形式，学生要通过弄清问题来选择.

（2）在抛物线第二象限图像上是否存在一点M，使△MBC是以∠BCM为直角的直角三角形，若存在，求出点M的坐标；若不存在，请说明理由.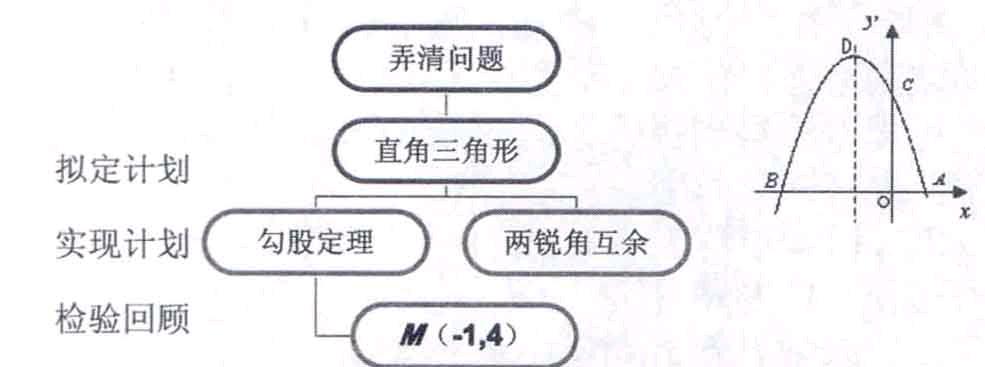

学生活动：学生小组讨论，合作探究，最后小组展示讲解.

设计意图：把三角形放在二次函数的图象中，使学生初步具有基本解决代数与几何综合题的能力.此题从直角的存在性出发，让学生回忆直角三角形在解题中的应用.一种是边的应用——勾股定理，一种是角的应用——两锐角互余.

老师点评：学生要弄清那个角是直角，动手作图，利用勾股定理或两锐角互余来实现计划，最后对各种解法进行比较分析，形成自己解决数学问题的一般策略.

（3）若E为抛物线B、C两点间图像上的一个动点（不与B、C重合），过E作EF与x轴垂直，交BC于F，设E点横坐标为x，EF的长度为L，求L关于x的函数关系式？并写出x的取值范围？

当E点运动到什么位置时，线段EF的长度最大，并求此时E点的坐标？

学生活动：学生独立思考.

设计意图：求两点距离的关键在于表示其坐标，并且字母越少越好.让学生体会变量在数学解题中的应用，体验数形结合解题的实用性和有效性.endprint

老师点评：学生能容易的发现两点的横坐标相同，进而制定计划用横坐标来表示两点的纵坐标，利用函数关系式来实现这个计划，最后检验回顾.让学生发现惯性思维的错误性，因为有的学生觉得点E是抛物线的顶点.

（4）在（3）的情况下直线BC与抛物线的对称轴交于点H.当E点运动到什么位置时，以点E、F、H、D为顶点的四边形为平行四边形？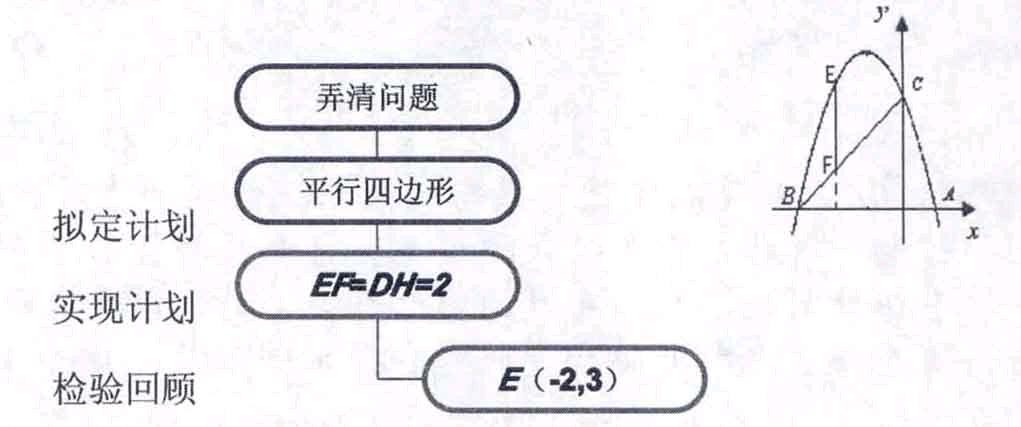

学生活动：学生独立完成.

设计意图：把平行四边形放在二次函数的图像中，使学生进一步具有基本解决代数与几何综合题的能力.让学生动手作平行四边形，来探究点的存在性.

老师点评：在平行四边形的作图中，要考虑已知点的连线段作为边和对角线两种情况，防止遗漏.

（5）在（3）的情況下点E运动到什么位置时，使△BCE的面积最大？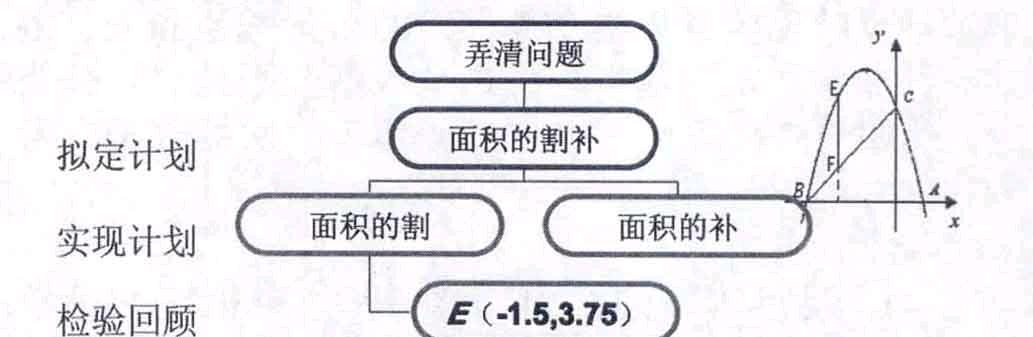

学生活动：学生小组讨论，合作探究，最后小组展示讲解.

设计意图：三角形的面积是常考题型.学生要善于发现图形特征，利用图形的割补思想，把不易表示的底与高转化为易表示的底与高，进而达到数学解题的目的.通过数学解题提高学生数形结合、化归的数学思想.

老师点评：利用线段EF的长度，学生容易将原三角形分割成两个三角形；不利用线段EF的长度，我们可以补形来解决问题.实现计划的难点是图形如何来割补，这是学生要多观察、总结、归纳的.

（三）归纳小结与板书设计

学生活动：学生自由发言.

设计意图：让学生所学、所感、所惑畅所欲言.感受学生的领悟能力，让学生发现自己对数形结合、化归思想的掌握程度，在做题过程中出现的问题进行反思，为以后进一步的学习打下基础.

老师点评：波利亚怎样解题表和思维导图的应用，理清解题思路，提高学生数学解题的能力.

参考文献：

[1]中华人民共和国教育部制定.义务教育数学课程标准（2011年版）[M].北京师范大学出版社，2012.

[2]乔治·波利亚.怎样解题——数学思维的新方法[M].上海科技教育出版社，2011.

[3]罗增儒.中学数学课例分析[M].陕西师范大学出版社，2001.endprint