CFRP约束钢管混凝土核心柱承载力简化分析

孙国帅，顾 威

(1.辽宁工业大学， 辽宁 锦州 121001； 2.辽宁省交通高等专科学校， 辽宁 沈阳 110122)

CFRP约束钢管混凝土核心柱承载力简化分析

孙国帅1，顾 威2

(1.辽宁工业大学， 辽宁 锦州 121001； 2.辽宁省交通高等专科学校， 辽宁 沈阳 110122)

为了推导CFRP环向约束钢管混凝土轴压短柱承载力计算公式，对该类构件的受力机理和破坏特征进行了理论分析。基于极限平衡原理和极限分析的基本假设，得到CFRP环向约束构件的承载力计算公式。为了验证理论公式的有效性，利用试验数据进行对比，结果表明：计算结果与试验结果吻合较好；极限承载力主要取决于由CFRP和钢管产生的约束效应。研究结论可为CFRP约束钢管混凝土结构的实践应用提供参考。

CFRP；钢管混凝土；轴压短柱；极限承载力

随着人类科技的不断发展，每当出现新的优良工程材料和结构形式时，工程结构领域都将迎来飞跃式的发展。研究人员利用混凝土在三向受压下强度提高的特点，研发出了各种新型结构构件，其中典型的结构构件形式有FRP环向约束混凝土构件和钢管混凝土构件，现已将其作为一种承压构件广泛应用于各类土木工程项目中。而对于桥梁等处于复杂自然环境中的钢管混凝土结构，当钢管受到外界较大腐蚀时，钢管混凝土承载力会大大缩减，会给结构带来安全隐患。因此，近年来，CFRP(碳纤维增强塑料)约束钢管混凝土构件逐渐受到研究人员的青睐。

本文根据课题组多年的研究成果，回顾了该类结构的研究现状，阐述了CFRP约束钢管混凝土轴压短柱的受力机理和破坏特征，在此基础上，推导了其承载力计算公式。

1 CFRP约束钢管混凝土结构

外层CFRP筒和中间层钢管共同对核心混凝土形成套箍约束作用。从受力机理上来讲形成了三种材料相互作用得的一种新的结构形式，其截面形式以圆截面为主，也有研究学者进行了方形截面的试验研究工作，如图1所示。目前，这种通过复合材料来增加钢管混凝土性能的结构形式，在降低钢管壁厚和强度、减轻自重方面占优势，同时，本文采用的碳纤维增强塑料还能够解决钢管混凝土结构的钢管易腐蚀问题，因此，其在新建结构材料选用以及既有钢管混凝土结构的增强加固领域有较好的研究价值[1]。

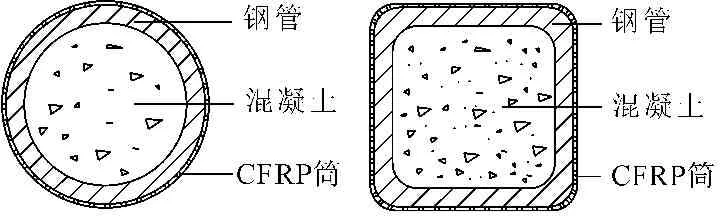
(a) 圆形截面 (b) 方形截面

图1 CFRP约束钢管混凝土构件截面

CFRP约束钢管混凝土结构自提出以来已经历10 a的研究历程，主要研究团队的研究成果已见诸国内外期刊并编入地方规程。赵颖华等[2-4]在CFRP-钢管混凝土往复荷载下力学响应、仿真分析以及基于声发射技术的破坏过程等方面做出了贡献；王庆利等[5]通过大量的试验研究了CFRP-钢管混凝土的受压、受弯及扭转性能；顾威和孙国帅等[6-9]在该类构件的稳定性分析以及受损加固等方面进行了大量的研究；叶勇等[10]分析了该类构件的抗震性能和滞回性能；单波等[11]在利用CFRP加强钢管混凝土的节点部位等领域做了大量研究工作；Kumar A P等[12]研究了静载及循环荷载下CFRP加强钢管结构的性能，结果表明CFRP的存在显著增强了结构的轴向承载力、延性和刚度；Sundarraja M等[13]进行了CFRP约束方截面钢管混凝土梁的实验研究，证实了随着CFRP层数的增加，弯曲构件的延性指标降低，而承载能力和刚度有所增加等[14-16]。

2 CFRP约束钢管混凝土结构受力性能的研究

2.1 工作机理和破坏特征

该类构件的工作机理就是充分利用碳纤维增强塑料、钢管和核心混凝土三种材料的力学特性，达到混凝土三向受压的效果，提高整个复合结构的承载能力。CFRP约束钢管混凝土结构承载的生命周期主要分为以下四个阶段：

(1) 初始承载阶段。CFRP约束效果不明显，钢管和核心混凝土各自独立地承受纵向压力，此阶段，钢管与混凝土之间不发生挤压。

(2) 持续承载阶段。随着持续承载，核心混凝土的不断侧向膨胀使三种材料的受力状态发生了改变，其受力机理如图2所示。此时，钢管的主要贡献已逐渐从纵向受压转变为环向受拉。

(3) 钢管屈服后的塑流阶段。此阶段为CFRP约束钢管后，强化混凝土套箍效应的增益，构件的受力性能得到明显提高。

(4) 失效阶段。针对短柱，在CFRP断裂时达到极限状态，然后荷载开始下降，变形不断增加，试件破坏，图3为课题组进行CFRP环向约束钢管混凝土结构试验和数值模拟过程中得到的荷载与变形关系曲线，可以看出在CFRP断裂前构件的承载力达到极限值；图4为课题组进行CFRP环向约束钢管混凝土结构试验中一组轴压短柱的破坏情况。

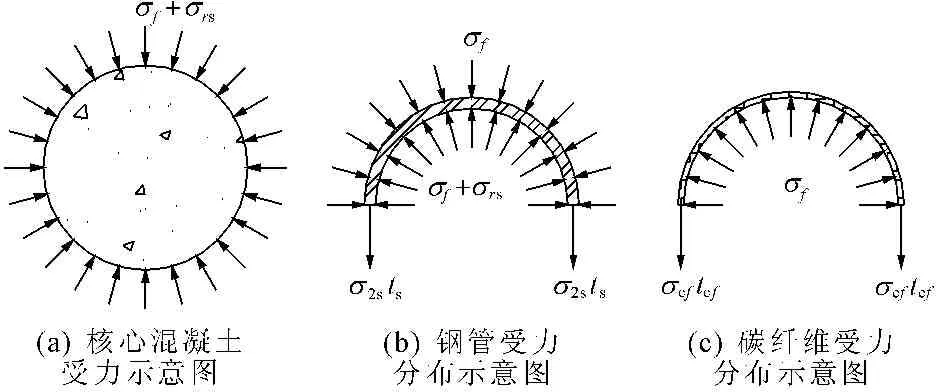
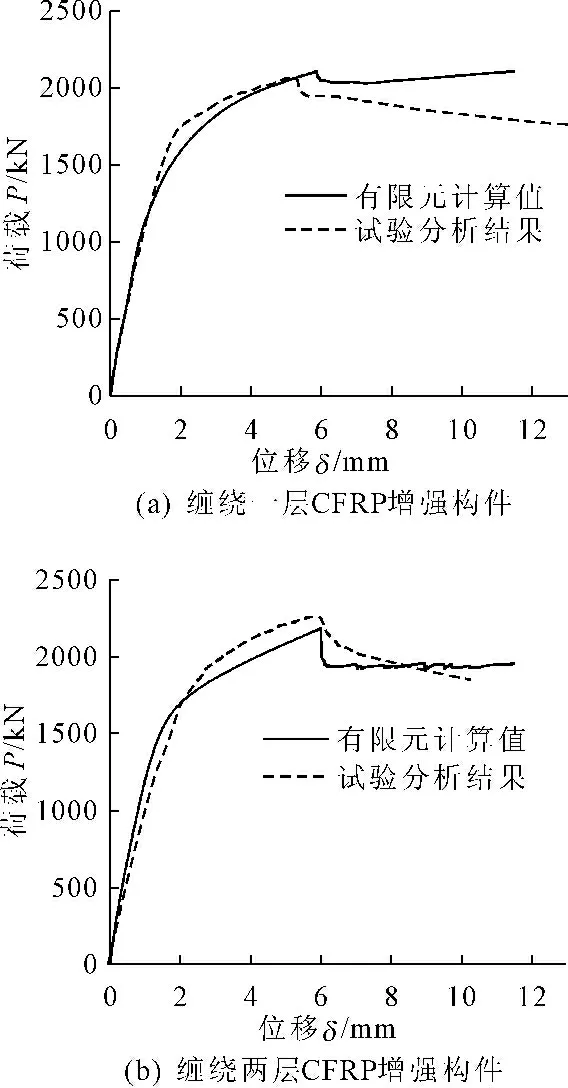
图2 圆CFRP-钢管混凝土受力特点

图3 构件荷载-纵向位移曲线

2.2 CFRP-钢管混凝土承载力计算公式

2.2.1 极限平衡理论

极限平衡理论[17-18]是忽略一些复杂因素，不管加载历史和变形过程，对理论模型进行简化，对极限条件列出静力平衡方程。应用该理论得到的极限承载力应该与通过全过程分析法获得值在理论上是相同的。

图4 CFRP断裂前后对比

根据《建筑结构可靠度设计统一标准》[19](GB50068—2001)，极限平衡理论涉及到的极限状态是指达到最大承载能力或发生不适于继续承载的较大变形，分别对应脆性和塑性破坏两种情况。对于本文研究的CFRP约束钢管混凝土构件，一般短柱属于脆性破坏，而较长柱则属于塑性破坏。

2.2.2 CFRP约束钢管混凝土轴压短柱极限分析的基本假设

(1) 将CFRP环向增强该类构件进行分解，整个结构体系分为CFRP筒、钢管和核心混凝土三部分。

(2) CFRP环向增强该类构件轴心受压时构件的应变场是轴对称的，且CFRP筒、钢管和混凝土的极限条件是稳定的。

(3) 核心混凝土处于三向受压状态；钢管为理想弹塑性材料，采用Von Mises屈服准则，忽略其径向应力，但径向应变值不等于零，沿壁厚方向其径向应力和环向应力是均匀分布的；CFRP符合线弹性关系，处于环向受拉状态，在极限状态时，达到拉伸强度fcf(断裂)。

2.2.3 极限承载力计算公式推导

(1) 建立轴心受压构件静力平衡方程。根据假设，由静力平衡条件，建立如下平衡方程：

N=N1+N2=fckAc+kpAc+fsAs

(1)

式中：N为轴心受压构件承载力；N1、N2分别构件混凝土和中间层钢管所承担的承载力；Ac、As分别为CFRP约束钢管混凝土构件混凝土和中间层钢管的横截面面积；fck为混凝土轴心抗压强度标准值；fs为钢管纵向应力；k为核心混凝土强度提高系数；p为等侧压力。

(2) 混凝土强度提高系数k与侧压力p的确定。由图2三种元件的静力平衡条件可得：

p=σf+σrs

(2)

根据图5所示的钢管平衡条件：

(3)

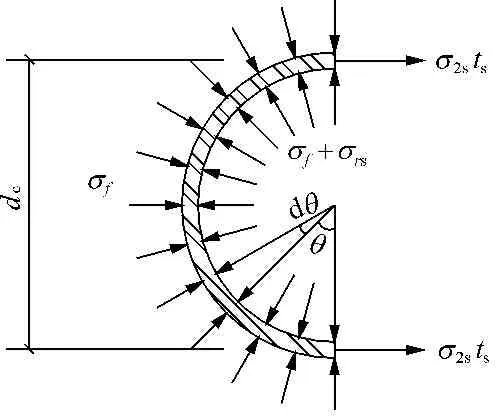
(4)

图5 钢管应力平衡示意图

当钢管的纵向应力达到屈服时，其环向应力不应超过钢管的屈服强度，有：

(5)

(6)

同理，

(7)

所以，

(8)

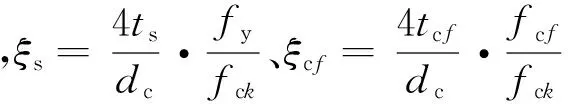
根据混凝土在复杂应力状态下的统一强度准则，可得：

(9)

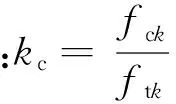
(3) 核心混凝土部分承载力计算

(10)

(4) 钢管的纵向应力计算。根据钢管的平衡条件：

(11)

钢管服从Von Mises屈服条件：

(12)

由于：

(13)

所以，得到：

(14)

(5) 构件的极限承载力计算。根据假设，该类构件的极限状态是CFRP即将断裂，CFRP约束下的钢管产生的约束效应达到极限，有：

(15)

可见，在构件几何尺寸和材料性质一定的情况下，极限承载力与约束效应系数有密切的关系，即约束效应系数的大小决定着CFRP环向增强钢管混凝土核心柱极限承载力的值。

3 试验验证

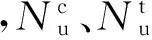
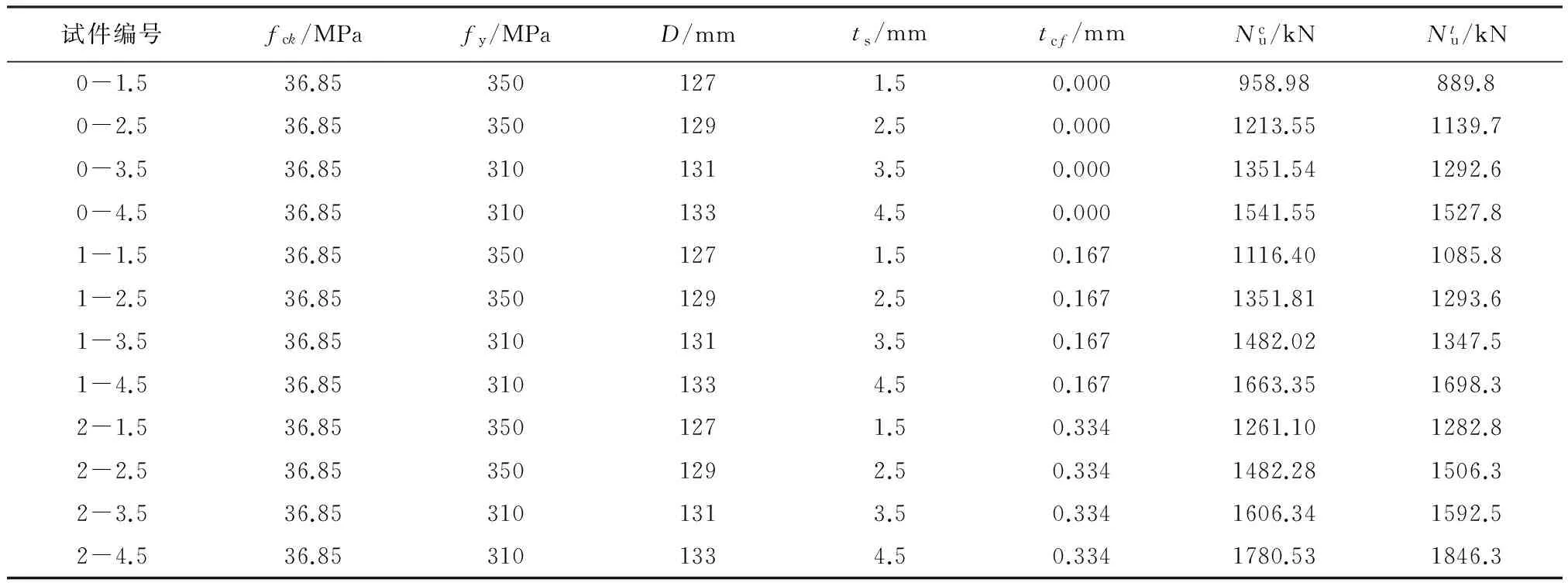
表1 计算结果与文献[20]试验结果对比

图6给出了不同钢管厚度和不同CFRP约束层数下计算值与试验值比较情况，可以看出，除了1-3.5试件试验值离散型稍大外，利用本文推导的CFRP环向增强钢管混凝土轴压短柱计算公式的计算结果与试验结果吻合较好。此外，当钢管厚度不变时，无论是理论值还是计算值，极限承载力随着CFRP厚度的增加而增大；而当CFRP厚度不变时，极限承载力随钢管壁厚增加而增大，验证了前面公式(15)中构件极限承载力主要受约束效应系数影响的关系。

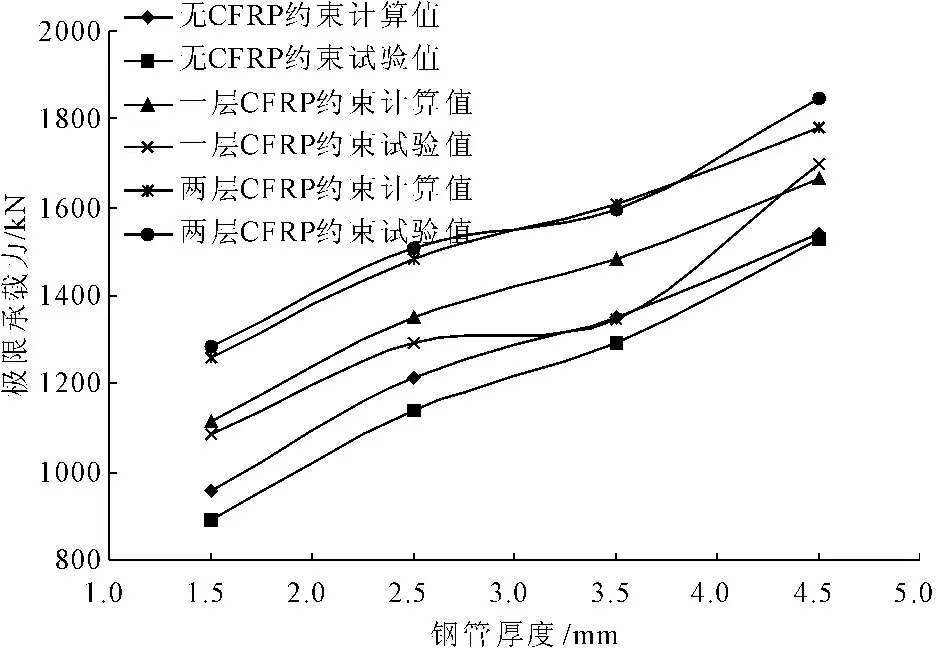
图6 不同钢管厚度和不同CFRP约束层数下计算值与试验值比较情况

4 结 论

本文通过对CFRP环向增强钢管混凝土核心短柱极限承载力的计算公式推导及试验验证，可以得出以下结论：

(1) 根据本文提出的基本假设，建立了CFRP环向约束钢管混凝土轴压短柱的极限承载力简化计算公式，与试验结果的对比分析显示结果吻合较好，验证了其合理性和有效性；

(2)CFRP环向增强钢管混凝土构件发生脆性破坏时，其极限承载力在各材料参数相同情况下，其值取决于由CFRP筒和钢管产生的约束效应，即主要与约束效应系数有关；

(3) 根据本文计算公式得出的承载力值为构件所能承受的最大承载力，结果可以为CFRP环向增强钢管混凝土构件的设计、检测和加固等实践应用提供参考和理论依据。

[1] 孙国帅,于铁汉,董松员,等.CFRP-钢管混凝土结构的发展与研究综述[J].工业建筑,2007,37(S1):584-587.

[2] 朱春阳，赵颖华，高 爽.往复荷载作用下GFRP/CFRP混合-钢管混凝土力学响应[C]//Proceedingsofthe11thChina-JapanJointConferenceonCompositeMaterials，2014.

[3]ZhuCY,ZhaoYH,GaoS,etal.Mechanicalbehaviorofconcretefilledglassfiberreinforcedpolymer-steeltubeundercyclicloading[J].JournalofZhejiangUniversitySCIENCEA, 2013,14(11):778-788.

[4] 陈 忱.FRP钢管混凝土构件抗冲击性能研究[D].大连：大连海事大学，2016.

[5] 王庆利，冯立明，屈绍娥.圆钢管混凝土轴压短柱在长期荷载-氯盐腐蚀耦合作用下的试验研究[J].土木工程学报，2015,48(S1)：48-52.

[6] 顾 威，李宏男，孙国帅.CFRP加固受损钢管混凝土轴压柱试验研究[J].建筑材料学报，2013，16(1)：138-142.

[7] 孙国帅，赵颖华，顾 威，等.长径比对CFRP-钢管混凝土轴压柱承载力的影响[J].四川建筑科学研究，2007，33(5)：12-16.

[8]SunGS,ZhaoYH,GuW.StabilityofconcretefilledCFRP-steeltubeunderaxialcompression[C]//JohnnyVN.ProceedingsofTubularStructuresXII,BocaRaton:CRCPress, 2008:111-116.

[9] 顾 威.CFRP钢管混凝土柱的力学性能研究[D].大连：大连海事大学,2007.

[10] 叶 勇，韩林海，陶 忠.脱空对圆钢管混凝土受剪性能的影响分析[J].工程力学，2016，33(S1)：62-66.

[11] 单 波，刘 波，肖 岩，等.大尺寸CFRP约束混凝土方柱落锤动态冲击试验研究[J].振动与冲击，2016，35(20)：90-97.

[12]KumarAP,SenthilR.AxialbehaviourofCFRP-strengthenedcircularsteelhollowsections[J].ArabianJournalforScienceandEngineering, 2016,41(10):1-10.

[13]SundarrajaMC,PrabhuGG.ExperimentalinvestigationonstrengtheningofCFSTmembersunderflexureusingCFRPfabric[J].ArabianJournalforScienceandEngineering, 2014,39(2):659-668.

[14] 梁炯丰，郭立湘，易萍华，等.方形CFRP钢管约束再生混凝土轴压长柱试验研究[J].混凝土，2016(7)：34-36.

[15] 杜 仇,刘永军,李锡鑫.爆炸荷载下圆截面钢-混凝土-CFRP-混凝土组合柱动力响应数值模拟[J].水利与建筑工程学报,2016,14(5):55-60.

[16] 宋志刚,樊 成,宋 力.GFRP管混凝土轴压短柱承载力研究[J].水利与建筑工程学报,2017,15(2):71-75.

[17] 陈建伟,苏幼坡,陈海彬,等.基于极限平衡理论的复式钢管混凝土轴心受压承载力计算方法[J].土木工程学报,2013，46(S1):106-110.

[18] 李 斌.钢管混凝土结构的研究[D].西安：西安建筑科技大学,2004.

[19] 中华人民共和国建设部.建筑结构可靠度设计统一标准：GB50068—2001[S].北京：中国建筑工业出版社，2001.

[20] 顾 威，关崇伟，赵颖华，等.圆CFRP钢复合管混凝土轴压短柱试验研究[J].沈阳建筑工程学院学报(自然科学版)，2004，20(2)：118-120.

Simplified Analysis of Bearing Capacity of Concrete Filled Steel Tubular Core Columns with CFRP Composite Materials

SUN Guoshuai1, GU Wei2

(1.LiaoningUniversityofTechnology,Jinzhou,Liaoning121001,China;
2.LiaoningCollegeofCommunication,Shenyang,Liaoning110122,China)

To derived the calculation formula of bearing capacity of concrete filled steel tubular core columns with CFRP composite materials, the mechanical mechanism and failure characteristics are investigated theoretically. Based on the basic assumptions of limit analysis, the calculation formula of bearing capacity of concrete filled steel tubular core columns with CFRP composite materials is given by limit equilibrium theory. In order to validate the formula, the calculated results of the proposed method agree with the experimental ones reported in other paper. And the bearing capacity of specimen depend on the effect of restraint from CFRP and steel tube. The conclusion can provide references for the practical application of concrete filled steel tubular structure with CFRP composite materials.

CFRP; concrete filled steel tube; short column with axially load; ultimate bearing capacity

10.3969/j.issn.1672-1144.2017.04.014

2017-04-02

2017-05-03

辽宁省教育厅基金项目(JW201615406)；辽宁工业大学教师科研启动基金项目(X201406)

孙国帅(1979—)，男，辽宁锦州人，博士，讲师，主要从事工程管理和组合结构方面的工作。E-mail:gs.sun@aliyun.com

TU393

A

1672—1144(2017)04—0074—05