扩孔型端板连接新型钢结构节点恢复力模型

黄冀卓，朱骏球，林楚修

(福州大学 土木工程学院， 福建 福州 350116)

扩孔型端板连接新型钢结构节点恢复力模型

黄冀卓，朱骏球，林楚修

(福州大学 土木工程学院， 福建 福州 350116)

建立了一种采用扩孔连接的新型钢结构端板节点恢复力模型。首先在分析节点试验滞回曲线规律的前提下，将节点滞回曲线分解为弹性段、滑移段和滑移承压段三个不同的简化模型，并提出相应的滞回规则；然后应用数值分析与拟合等方法确定了简化滞回模型中的各关键特征参数，并结合已有的骨架曲线模型建立了该新型节点的恢复力模型。通过与试验滞回曲线的对比，验证了新型节点恢复力模型的准确性。该恢复力模型计算简单、滞回规则清晰，可为扩孔型端板连接新型钢结构节点在地震区的应用提供理论依据。

端板；节点；扩孔；滞回规则；钢结构；恢复力模型

与传统的焊接节点相比[1]，通过螺栓连接的半刚性钢节点具有更好的塑性转动和耗能能力[1-2]。常见的半刚性钢节点包括短T型钢连接[3-4]、顶底角钢连接[5]和端板连接[6-12]等节点类型，其中端板连接节点，特别是当端板较厚时，其具有较大的初始转动刚度，因而可被应用于地震区的钢结构设计中[13]。值得注意的是，对于短T型钢和顶底角钢等半刚性连接节点，其连接件是和梁、柱构件分离的；而在端板连接节点中，端板是与钢梁通过焊接形成一个整体。构造上的不同导致节点在后续的震后修复难度和成本上存在明显差异。前者修复简单、成本低廉，而后者由于需要同时替换端板和钢梁，因此修复难度和维修成本均增加。

为改善传统端板节点存在的弊端，文献[14]提出了一种新型分离式端板连接节点，如图1所示。该分离式端板连接件共由4块钢板焊接而成，包括端板、翼缘连接板和腹板连接板等组成部分，其与梁、柱之间均通过螺栓连接。与此同时，为了进一步提高该新型节点的转动、延性和耗能能力，连接钢梁的翼缘和腹板连接板上均采用具有一定扩孔尺寸的长圆螺栓孔来替代普通圆孔。文献[14]开展了该新型端板连接节点在不同扩孔尺寸下的系列试验研究，文献[15]在此基础上给出了该新型节点的骨架曲线模型。

图1 扩孔型端板连接节点

为了能更好地掌握该新型节点的恢复力模型，本文将基于已有试验成果，同时结合文献[15]中的四折线骨架曲线模型，进一步建立适用于该类新型节点的恢复力模型。

1 新型节点试验方案及结果简介

基于不同的扩孔尺寸，文献[14]进行了4个新型节点的足尺试验，节点构造和尺寸如图2所示，4个节点的编号为D-d(d表示扩孔尺寸，分别取0 mm，2 mm，4 mm和6 mm)。所有节点的梁、柱截面均相同，钢梁为H350×200×10×16，钢材为Q235B；钢柱为H700×300×24×36，钢材为Q345B。

试验采用位移进行循环加载，图3给出了4个节点的弯矩M-转角θ试验滞回曲线。由图3可以看出，4个新型节点滞回曲线整体形状相似，均有明显的捏拢现象，且随着扩孔尺寸增大，滞回曲线的包络面积也越大，节点的延性和耗能能力也更强。

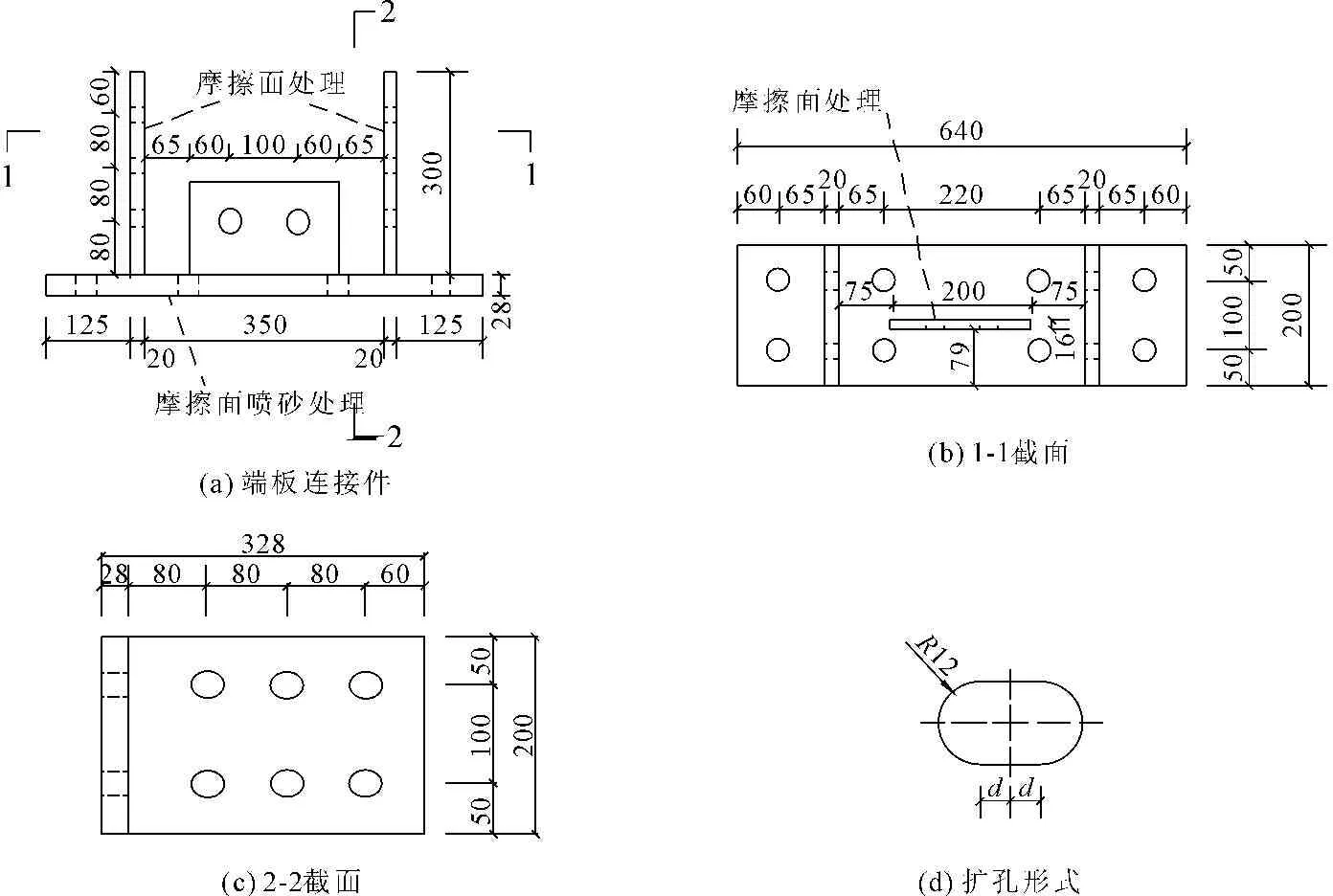
图2 端板连接件(单位：mm)

2 滞回规则的简化

通过对图3中各节点试验滞回曲线分析可以发现，该新型节点在往复荷载作用下分别经历了初始弹性、滑移和滑移承压三个阶段。图4给出了不同阶段下新型节点滞回曲线的简化模型，该三阶段简化滞回模型的走势规律为：(1) 正、反向加、卸载曲线对称；(2) 在弹性阶段，节点加载刚度与卸载刚度相同；(3) 在弹性阶段之后，节点的卸载刚度、捏拢点和承压点弯矩均存在退化现象；(4) 节点由卸载点卸载并再加载至捏拢点之间的滞回曲线刚度保持一致；(5) 各级加载循环曲线在经过捏拢滑移平台之后将指向上一次同向加载循环曲线的卸载点继续加载。

由图4可知，只要确定了图中的若干关键参数，即可清晰描述该新型节点的全过程滞回曲线。

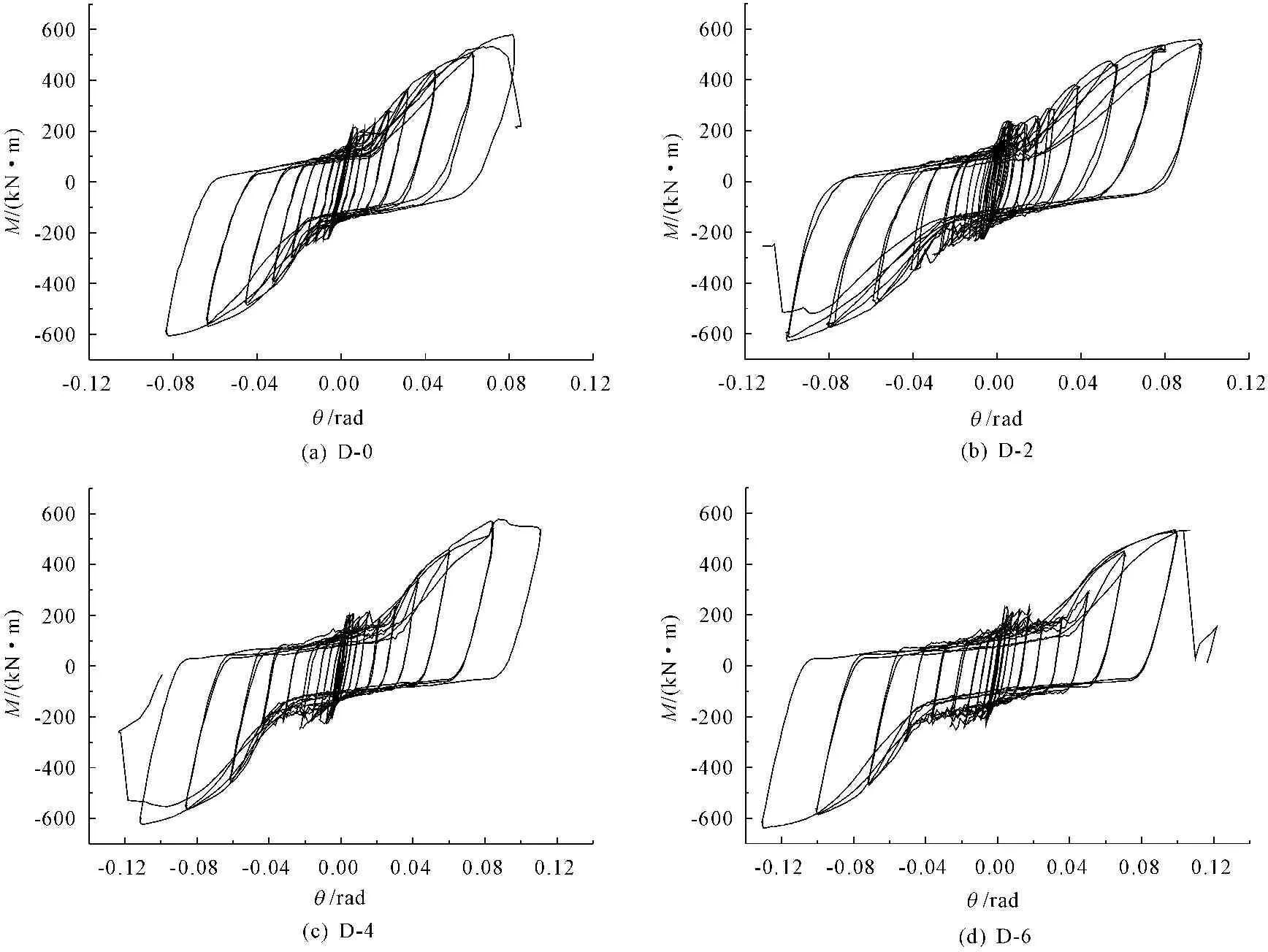
图3 新型节点的弯矩M-转角θ试验滞回曲线

图4 新型节点处于不同阶段的简化滞回曲线

3 滞回规则参数的确定

3.1 卸载刚度Kr

根据上述假定，当加载级处于弹性阶段时新型节点的卸载刚度Kr1与弹性阶段刚度K1相同：

Kr1=K1

(1)

在达到滑移阶段之后，新型节点各级循环的卸载刚度Kr2,i均有较为明显的退化趋势。对试验数据进行无量纲化[1]处理，用Kr2,i/K1、θmax,i/θA作为纵坐标和横坐标变量，可以绘制出D-0、D-2、D-4和D-6节点在各级循环下的无量纲卸载刚度与转角的关系(见图5)，其中θmax,i为卸载点转角，i为节点进入滑移阶段之后的加载循环次数，其数值等于当前加载级下的累积循环次数扣除弹性阶段的加载循环次数，QA为骨架曲线模型中的滑移转角。

图5 卸载刚度拟合曲线

对图5中的数据进行拟合，由图5可以看出拟合曲线与卸载刚度的退化趋势相近，以对数函数的形式退化，拟合出的卸载刚度退化方程如下：

Kr2,i/K1=-0.101ln(θmax,i/θA)+0.9372

(2)

3.2 捏拢点弯矩ME,i及转角θE,i

图6为新型节点捏拢点弯矩与加载次数的关系图，从图6中可以看出新型节点的正向与负向捏拢点弯矩随加载循环次数的增加呈现明显的线性退化趋势，因此本文以加载循环次数i 作为参数建立其退化方程：

(3)

式中：ME,i为新型节点各级循环曲线捏拢点弯矩；i含义同前，即为节点进入滑移阶段之后的加载循环次数；MA为骨架曲线滑移弯矩(本文将其视为捏拢点弯矩的初始值)；μ1为捏拢点弯矩退化参数。

提升水质保障。2016年，省水利厅出台《关于加强农村饮水安全工程水质检测工作的实施意见》，从检测单位、检测指标、检测频率等方面提出明确要求。各县（区）建立了完整的水质监测体系，根据检测结果，制定解决措施和办法，全力保障水质安全。2017年以来，年均集中培训检测人员400余人，年均检测水样近3万份。

图7列出了D-0、D-2、D-4、D-6节点相邻两次的捏拢点弯矩比值，并同时计算出其平均值为0.91(图7中横线)。由图7可知，该平均值可近似作为捏拢点弯矩退化参数μ1。于是新型节点的各级循环捏拢点弯矩可表达为：

ME,i=0.91iMA

(4)

各级循环的捏拢点转角θE,i则可根据捏拢点弯矩ME,i、对应的卸载点弯矩Mmax,i、卸载点转角θmax,i以及卸载刚度Kr2,i求出：

(5)

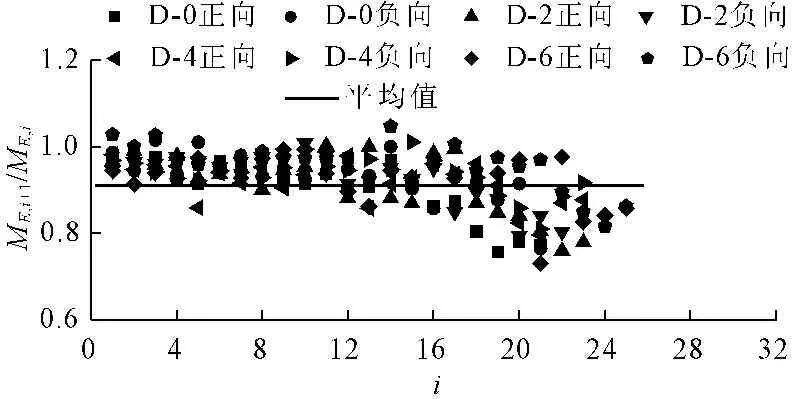
图6 各级循环下捏拢点弯矩变化规律

图7 捏拢点弯矩退化参数

3.3 承压点弯矩MF,i及转角θF,i

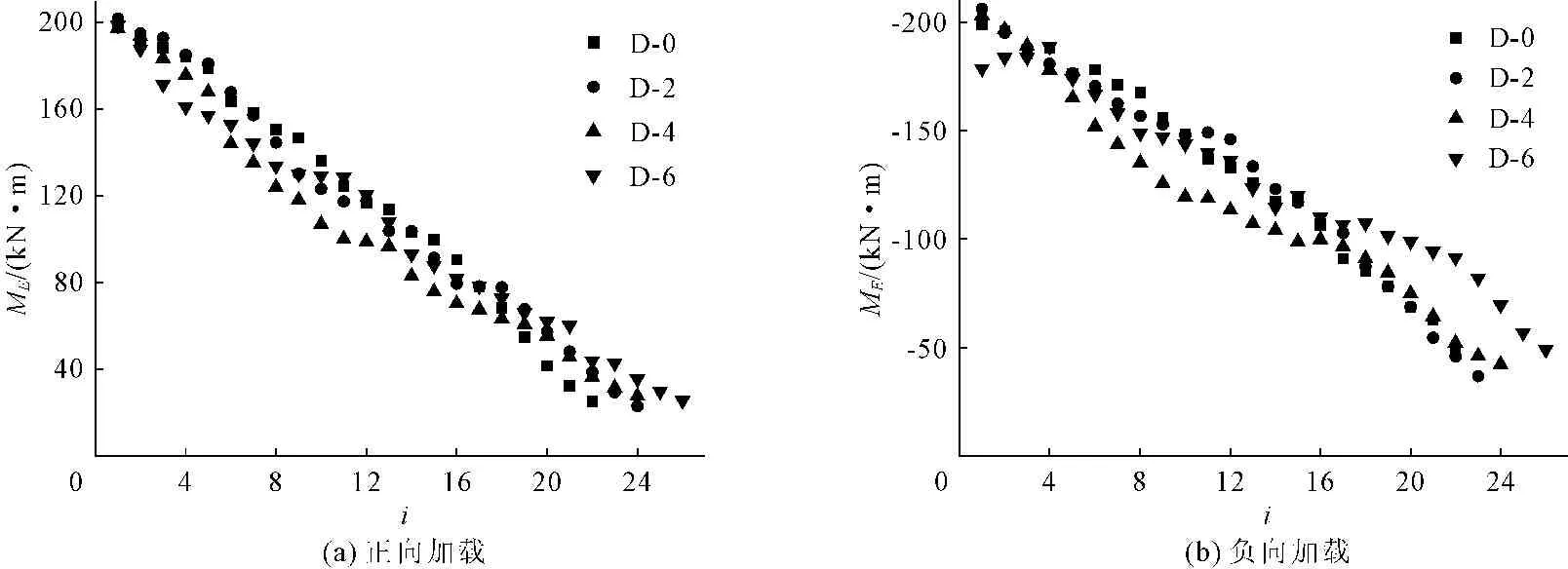
图8为新型节点承压点弯矩与加载循环次数的关系图，从图8中可以看出承压点弯矩MF,i数据相对离散，但有较为明显的退化趋势，因此同样认为其退化规律与加载循环次数i有关。承压点弯矩MF,i退化方程建议采用公式(6)计算：

(6)

式中：MF，i为节点各级循环曲线承压点弯矩；i为节点在螺栓承压之后的加载循环次数，其数值等于当前加载级下的累积循环次数扣除加载级处于弹性阶段与滑移阶段时的加载循环次数；MB为骨架曲线承压弯矩(本文将其视为承压点弯矩的初始值)，μ2为承压点弯矩退化参数。

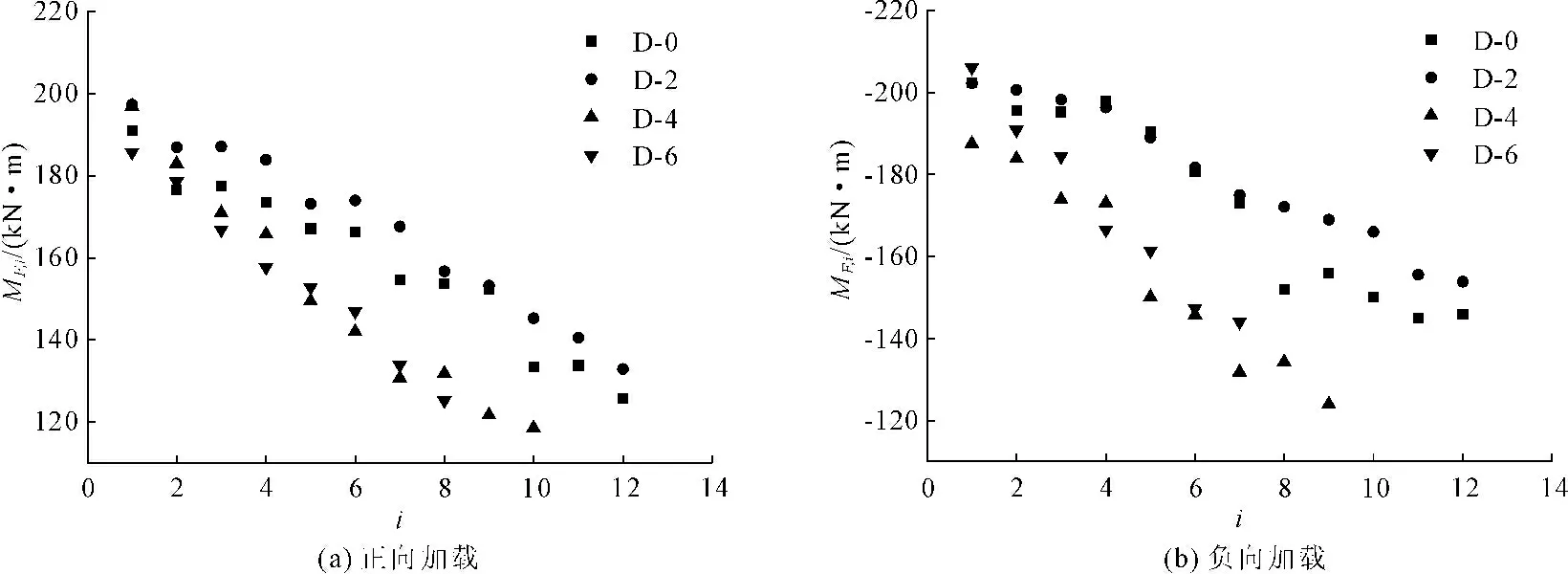
图8 各级循环下承压点弯矩变化规律

计算各新型节点相邻两次的承压点弯矩比值，列于图9中，其平均值为0.96(图9中横线)。由图9可知，各承压点弯矩比值点较为平均地分布于平均线两侧，因此可取承压点弯矩退化参数μ2=0.96，则新型节点的各级循环承压点弯矩可由下式确定：

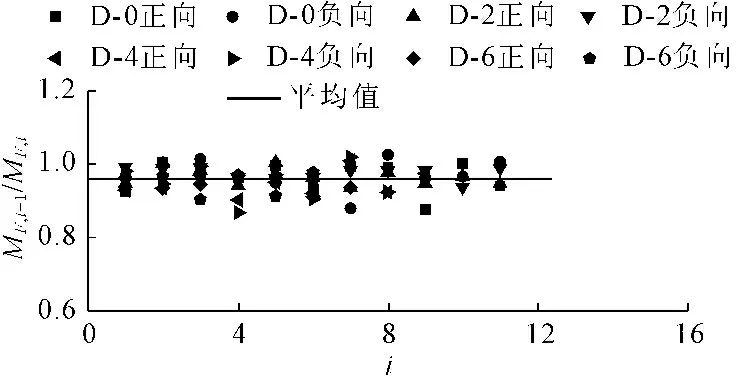
MF,i=0.96iMB (7)

图9 承压点弯矩退化参数

通过对各新型节点滞回曲线分析可知，随着加载循环次数的增加，承压点转角θF,i也随之增大，这主要是由于节点的塑性随着循环次数的增加而不断发展，端板连接件及梁构件的塑性变形增大了承压点转角。图10为新型节点承压点转角与加载循环次数的关系图，从图10中可以看出承压点转角θF,i基本随着循环次数的增加而呈递增关系，因此亦认为其与加载循环次数i有关。承压点转角θF,i退化方程建议采用公式(8)计算：

(8)

图10 承压点转角变化规律

计算各新型节点相邻两次的承压点转角比值，列于图11中。同样可以发现所有比值均比较集中地分列于其平均值(1.04)两侧，因此可取承压点转角增大参数μ3=1.04，于是新型节点的各级循环承压点转角可表达为：

θF,i=1.04iθB

(9)

3.4 捏拢滑移刚度

当加载级处于滑移阶段时，滞回曲线的捏拢滑移刚度取为捏拢点与上一次循环的反向卸载点间的割线刚度，按式(10)计算；

(10)

当加载级处于滑移承压阶段时，滞回曲线的捏拢滑移刚度Kr3,i为捏拢点与承压点间的割线刚度，按式(11)计算。

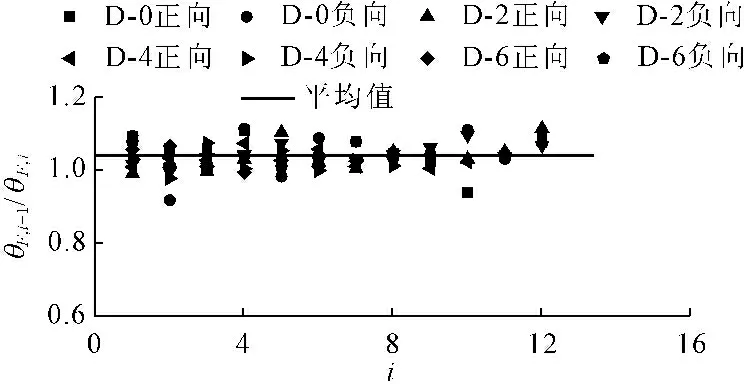
(11)

图11 承压点转角增大参数

4 恢复力模型的建立

综合以上分析，根据文献[15]所建立的骨架曲线模型和本文提出的滞回规则及特征点参数，可建立扩孔型端板连接节点的恢复力模型，如图12所示。

恢复力模型的行走路径为：

(1) 弹性阶段：加载和卸载均沿着骨架曲线弹性阶段进行，即正向加载刚度及反向加载刚度均为初始转动刚度K1，正向卸载刚度以及反向卸载刚度均为Kr1(=K1、式(1))。

(2) 滑移阶段：从卸载点2按卸载刚度Kr2i(式(2))经过卸载和再加载阶段到达捏拢点3(式(4)、式(5))，随后按捏拢滑移刚度Kr3,i(式(10))再加载至上一次加载的卸载点4，再从卸载点4点按卸载刚度Kr2,i(式(2))经过卸载和再加载阶段到捏拢点5(式(4)、式(5))，随后按捏拢滑移刚度Kr3,i(式(10))再加载至上一次加载的卸载点2(若该次循环卸载点与上一次循环不同，则继续沿骨架曲线加载至该次循环卸载点)。

(3) 滑移承压阶段：从卸载点12点按卸载刚度Kr2,i(式(2))经过卸载和再加载阶段到达捏拢点13(式(4)、式(5))，按捏拢滑移刚度Kr3,i(式(11))经过捏拢滑移平台到达承压点14(式(7)、式(9))，随后再加载至上一次加载的卸载点15，再从卸载点15点按卸载刚度Kr2,i(式(2))经过卸载和再加载阶段到捏拢点16(式(4)、式(5))，按捏拢滑移刚度Kr3,i(式(11))经过捏拢滑移平台到达承压点17(式(7)、式(9))，随后再加载至上一次加载的卸载点12(若该次循环卸载点与上一次循环不同，则继续沿骨架曲线加载至该次循环卸载点)。

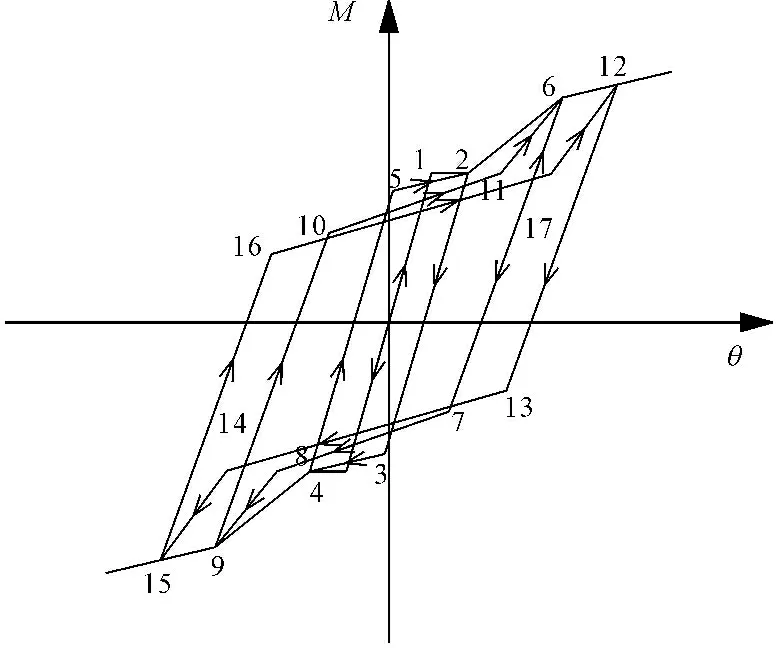
图12 新型节点恢复力模型

5 恢复力模型与试验结果对比

运用本文提出的新型节点恢复力模型绘制D-0、D-2、D-4和D-6节点滞回曲线，并将其与试验滞回曲线进行对比，如图13所示。从整体上看，各节点恢复力模型曲线与试验滞回曲线比较贴近，其包络面积相近，且各关键点(如捏拢点、承压点等)及各刚度参数均比较接近。由此验证了本文针对新型节点建立的恢复力模型的准确性，这为该类新型节点的工程应用，特别是弹塑性反应分析奠定基础。需要说明的是，D-0节点的恢复力模型曲线在循环初期几乎没有滑移段，与试验滞回曲线略有差异，这主要是因为D-0的恢复力模型是按照扩孔参数为0 mm进行计算的，而在实际试验节点中，螺杆与孔壁之间是存在1 mm～1.5 mm的间隙。

6 结 论

针对一种采用扩孔形式的新型端板连接节点，本文通过对已有节点试验的滞回曲线走势规律进行分析，提出了该新型节点的简化滞回模型，并应用数值分析与拟合等方法确定了简化滞回模型中各关键特征参数。通过与试验滞回曲线的对比，验证了本文所提出的新型节点简化滞回模型的有效性和准确性。该恢复力模型的建立，可为采用新型节点连接的钢框架结构弹塑性分析提供借鉴。

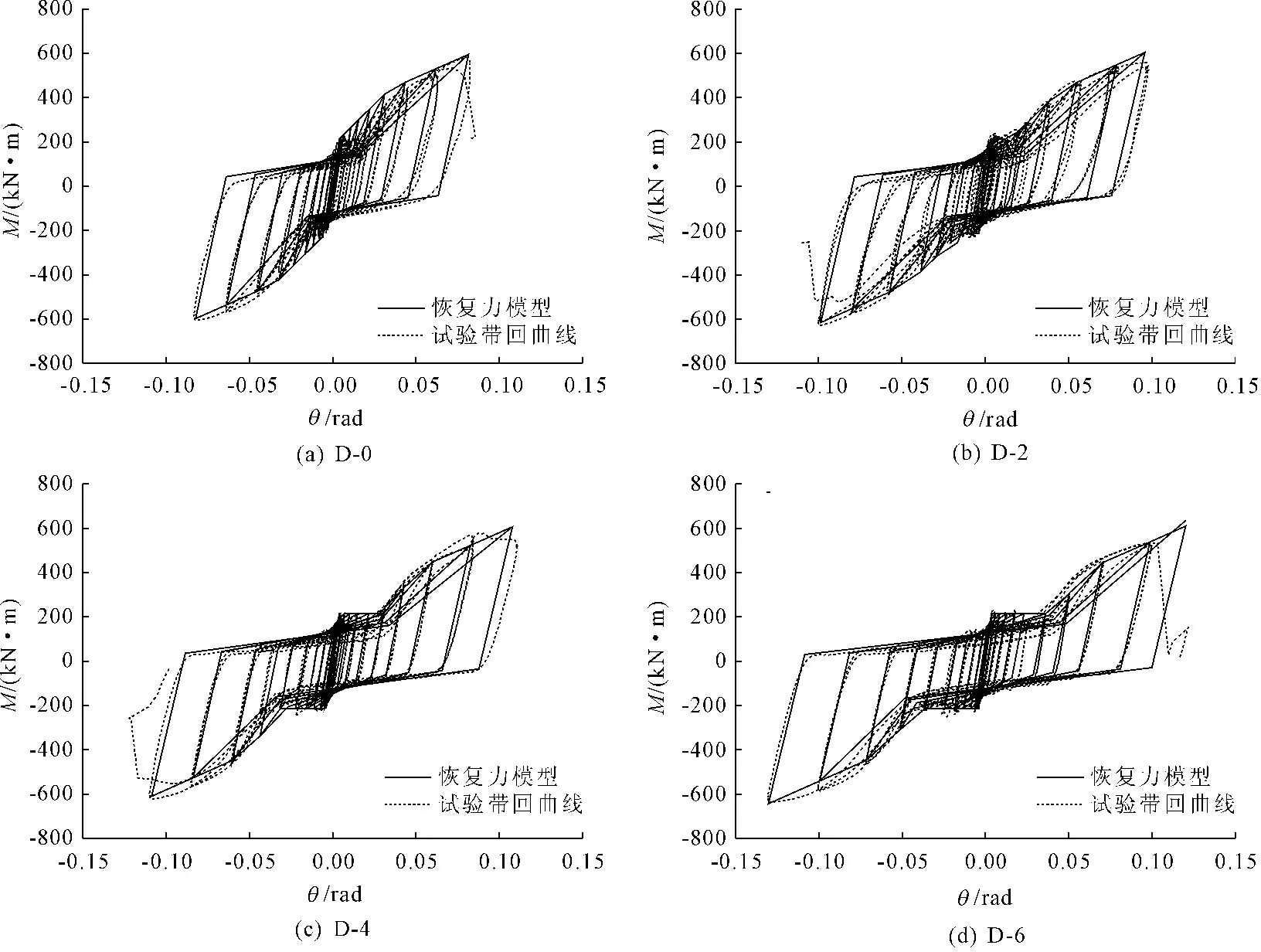
图13 新型节点恢复力模型与试验滞回曲线比较

[1] Chen W F, Goto Y, Liew J Y R. Stability design of semi-rigid frames[J]. Journal of Constructional Steel Research, 1996,38(1):89-91.

[2] Faella C, Piluso V, Rizzano G. Structural Steel Semirigid Connections: Theory, Design, and Software[M]. Boca Raton: CRC Press, 1999.

[3] Hu J W, Leon R T, Park T. Mechanical models for the analysis of bolted T-stub connections under cyclic loads[J]. Journal of Constructional Steel Research, 2012,78:45-57.

[4] Yang J G, Lee S K, Moon J K, et al. Prediction models for the initial rotational stiffness and ultimate plastic moment for a double split tee connection[J]. International Journal of Steel Structures, 2014,14(2):213-222.

[5] Abolmaali A S, Kukreti A R. Moment-rotation hysteresis behavior of top and seat angle steel frame connections[J]. Journal of Structural Engineering, 1999，125(8):810-820.

[6] Qiang Xuhong, Bijlaard Frans S K, Kolstein Henk, et al. Behaviour of beam-to-column high strength steel endplate connections under fire conditions-Part 1: Experimental study[J]. Engineering Structures, 2014,64(4):23-38.

[7] Mohamadi-shooreh M R, Mofid M. Parametric analyses on the initial stiffness of flush end-plate splice connections using FEM[J]. Journal of Constructional Steel Research, 2008,64(10):1129-1141.

[8] Guo Bing, Gu Qiang, Liu Feng. Experimental behavior of stiffened and unstiffened end-plate connections under cyclic loading[J]. Journal of Structural Engineering, 2006,132(9):1352-1357.

[9] 施 刚,石永久,王元清.钢框架梁柱端板连接的非线性有限元分析[J].工程力学,2008,25(12):79-85.

[10] 潘朝阳,樊宝锋,刘铭轩.循环荷载作用下梁柱半刚性连接钢框架受力特性分析[J].钢结构,2013,28(6):23-26.

[11] 王 涛.端板连接弯矩-转角关系及半刚性钢框架抗震性能的研究[D].广州：华南理工大学,2013.

[12] 雷 克,王先铁,张营营.钢管混凝土框架高强螺栓—端板节点的性能研究[J].水利与建筑工程学报,2010,8(3):150-153.

[13] American Institute of Steel Construction (AISC). Prequalified Connections for Special and Intermediate Steel Moment Frames for Seismic Applications: ANSI/AISC 358-16[S]． Draft Version, USA: Chicago (IL), 2015.

[14] 黄向宁.扩孔型端板连接钢结构新型节点性能研究[D].福州:福州大学,2014.

[15] 黄冀卓,庄元婷,林楚修.扩孔型端板连接新型钢结构节点骨架曲线模型[J].水利与建筑工程学报,2017,15(1):19-24,47.

Restoring Force Model for a New Type of End-plate Connections with Slotted Holes

HUANG Jizhuo, ZHU Junqiu, LIN Chuxiu

(CollegeofCivilEngineering,FuzhouUniversity,Fuzhou,Fujian350116,China)

Aiming at a new type of end-plate connections with slotted holes, restoring force model of this connection type was developed in this paper. Based on analysis of the tested hysteretic curves of connection specimens, the overall hysteretic curves of connections under cyclic load were decomposed into three simplified hysteretic models respectively corresponding to the three different behavioral phases: elasticity, slippage, and slippage combined with compression. Then, the hysteresis rules of such connections were proposed. By means of numerical analysis and fitting method, key characteristic parameters of the simplified hysteretic models were determined. Subsequently, restoring force model for this type of connections was developed in combination with the known skeleton curve model. The comparison results showed that the restoring force model for the new type of end-plate connections is in good agreement with the experimental results, which could provide theoretical support for the application of steel frames with this new-type connection in seismic areas.

end-plate; connection; slotted hole; hysteresis rule; steel structure; restoring force model

10.3969/j.issn.1672-1144.2017.04.002

2017-03-19

2017-04-26

国家自然科学基金项目(51278125)；福建省高等学校新世纪优秀人才支持计划项目(JA14026)

TU

A

1672—1144(2017)04—0006—07