改进蚁群算法在含DG配电系统可靠性评估应用

王 晨,刘 洪，钟建伟*,姜 芮,秦明亮

(1.湖北民族学院 信息工程学院,湖北 恩施 4450002; 2.国网恩施供电公司，湖北 恩施 445000；3.湖北省电力公司,湖北 武汉 430077)

改进蚁群算法在含DG配电系统可靠性评估应用

王 晨1,刘 洪2，钟建伟1*,姜 芮1,秦明亮3

(1.湖北民族学院 信息工程学院,湖北 恩施 4450002; 2.国网恩施供电公司，湖北 恩施 445000；3.湖北省电力公司,湖北 武汉 430077)

分布式电源(Distributed Generation,DG)接入配电网,使得网络的拓扑结构复杂性增加.使用最小路法能较好的分析此状态下的配电网,并且其计及了分支线保护等三方面的影响,能够处理有无备用电源和有无备用变压器的情况.在传统蚁群算法的基础之上通过使用轮盘赌与自适应信息素挥发系数对其进行改进,改进后的的蚁群算法收敛性大大提高,并通过Matlab验证了IEEE RBTS Bus6 系统F4的主馈线可靠性,结果表明该方法能很好的反映DG对配电网的供电可靠性影响,并且能快速分析配电网的拓扑结构,具有很强的实用性.

分布式电源；配电网；可靠性；蚁群算法；轮盘赌；自适应信息素挥发系数.

在电力系统中配电网是的作用把电网、电源与用户设备三者相互联接起来,其由输电线路、 一次配电线路、 配电站、 配电变压器、二次配电线路等组成.配电系统的可靠性指标实际上是整个电力系统结构及运行特性的集中反映[1-8].

据不完全统计,用户停电故障中80%以上是由电力系统中配电环节故障引起的[2].这说明配电系统可靠性对用户优质供电起关键作用,并且配电系统又有其自身的特点：其设备数目巨大,安装位置相对分散[2].因此如何快速的评估配电系统可靠性是保证用户优质供电的关键问题.

配电网可靠性评估技术的传统方法一般分为模拟法和解析法2 类[1].模拟法是利用统计学方法,对独立元件的故障概率进行采样与统计,计算并估计其元件状态.模拟法具有很强的灵活性,其缺点是计算时间长但精度低,其一般用于发、输电系统可靠性评估.解析法是利用元件的基本参数,建立其数学模型,并使用数值计算方法求得系统的可靠性指标.在现代大规模并行寻优的受自然启发的智能优化算法已成为许多学科的一个重要研究方向,如遗传算法、蚁群算法、粒子群优化算法、差分进化算法等[9-16]以成为研究的热点这些优化算法在处理非线性、多约束、多变量、不连续问题上克服了常规算法的局限性,显示出了很强的寻优能力.故此本文提出一种基于蚁群算法的最小路配电系统可靠性评估算法,能迅速、高效地解决配电网可靠性评估问题.

1 配电网可靠性指标与计算公式

负荷的停电时间以及停电次数主要影响配电系统供电可靠性,因此其定义为：衡量系统对用户持续供电能力,其定量化的表达方式为可靠性指标.配电系统可靠性指标可分为 2 类,一类是基本指标,另一类是配电系统的专用指标[17-23].

1.1 基本指标

常用的负荷指标有：负荷故障率λ(次/a)；负荷平均停电时间U(h/a)；负荷平均停电持续时间r(h/次).负荷与电源在正常配电网中一般为串联关系.计算公式如下：

λ=∑λi

(1)

U=∑λiri

(2)

r=U/λ

(3)

其中:λi为元件i的故障率,ri为元件 i 的平均修复时间.

1.2 专用指标

配电系统专用指标指反映系统停运的严重程度和重要性.其中包含[1]：

表1 专用指标的简写与英文全称

2 含DG的配电网可靠性评估

2.1 孤岛划分方法

本文应用文献[5]中关于孤岛的划分的办法.首先评估各负荷重要性,并且对重要性不同的负荷赋予不同的权重指标.其次定义等值负荷即：负荷的规模与负荷点的权重系数乘积.在含分布式电源配网中划分其孤岛.其目标为让孤岛里的等值负荷求和值为最高：

(4)

(5)

(6)

其中：E1max为负荷的等效和；ωi为负荷点i的权重系数；Li为负荷值；PDG为分布式电源的额定容量；D为孤岛中全体负荷点占有的拓扑面积.

2.2 含DG最小路法可靠性评估

配电系统在现实中一般使用开环运行并以辐射状供电方式,它是可靠性评估的典型方式,简单含DG的配电网接线图(见图1).对加入DG后配电网可靠性评估算法流程如图2,先计算电源到各负荷的最小路,之后将系统中在最小路上的元件规定为最小路元件,反之为非最小路元件.

图1 简单含DG的配电网接线图Fig.1 Simple containing DG distribution network wiring diagram

对于最小路上元件,从负荷点向回探查,沿最小路求各节点等效可靠性指标,最后计算出系统的可靠性指标；对于非最小路的元件,依据实际配电网结构将非最小路上可靠性指标归算到相应最小路上,进而对各个负荷点的可靠性指标.例如根据图1,相对于点B,支路a的可靠性需换算到点A上,主馈线负荷点LP3、LP4和分支线c、d的影响也需换算到B上,从而进行最小路中的元件与节点的计算.本算法统筹了各个支线保护、隔离开关、分段断路器和分布式电源对系统的作用,并只需进行最小路中元件与节点的计算.

图2 最小路算法流程图Fig.2 Shortest path algorithm flow chart

3 蚁群算法求最短路径

3.1 最短路径问题

定义在赋权图G(V,{E})中V是包含n个节点的集合,E是包含h条边(弧段)的集合,〈i,j〉是E中从节点i至j的边,ωi，j是边〈i,j〉所对应的的非负权值.定义a,b分别为图G(V,{E})中的起点和目标点,求图G(V,{E})的最优路径就是寻找从a点到b点的一条具有最小权值总和的路径.

3.2 蚁群算法求解最短路径

蚁群算法是由Dorigo、Maniezzo和Colorni等于1991年首先提出来，它属于自然启发式算法[24-26].蚁群算法的基本原理如是：在自然界中蚂蚁组成为群居社会,虽然蚂蚁单个个体行动简单,但由单个个体组成社会群体时,其群体行为却相当复杂.蚂蚁群体(社会)组成的最大特点是团队协作.蚂蚁之间团队协作表现最为突出的的一点就是觅食过程,蚂蚁之间通过寻找各个体间遗留的“信息素”多少,来寻找到到达“食物”处的最短路径.但是对于个体蚂蚁而言则难于登天.生物学家发现,虽然蚂蚁没有视觉但蚁群却可以轻而易举的找到从蚁穴到食物源的最短路径,这是因为蚂蚁个体之间在觅食过程中会分泌一种名之为“信息素”的物质,并使之粘附在所经过的路径上以向其它蚂蚁传递信息.首先其余蚂蚁可以“闻”到这种物质,其次其余蚂蚁可以判断“信息素”浓度的大小,已决定自己的行进方向.但是这种“信息素”有一种特点,其浓度会随着时间的推延而逐渐挥发,这就导致蚂蚁行进的路径长短和走过此路径上蚂蚁数量成为“信息素”的决定因素.如果走过这条路径上的蚁群越多那么其“信息素”的浓度会越高,进而会有更多的蚂蚁闻到这种“信息素”,选择从这条道路上走过的概率就会增大,与此同时,其它路径上的“信息素”会慢慢衰减,这样就形成了一种正反馈机制.最终蚁群会找到从“蚁穴”到“食物源”的最短路径.

1)在基本蚁群算法中设待求拓扑图为Path,蚂蚁的个数为m,点i与点j间距离为di,j,同时刻同路径的信息素浓度为τi,j.

2)蚂蚁开始爬行,蚂蚁从一点i选择到另一点j通过信息浓度来选择,并在其中用禁忌表tabu记录蚂蚁爬过的节.

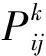
(7)

其中:ηij表示路径(i,j)的能见度,反映由节点i转移到节点j的启发程度.α表示信息启发式因子,β表示启发式因子,allowed表示蚂蚁k下一步允许选择的节点集合，则有:allowed=1-tabu.由于挥发性是信息素的主要特征,故而蚂蚁个体在走过n节点时,信息素浓度会有所挥发,需要对信息素浓度进行更新.其信息素浓度更新公式为:

(8)

(9)

其中:k表示第k个蚂蚁,t+n为时刻,P为信息素蒸发系数,值在(0,1)之间 ,Δτij表示本次迭代中“信息素”增量,初值置0.蚁群算法流程图如图3所示.

图3 蚁群算法流程图Fig.3 Ant colony algorithm flow chart

传统蚁群算法拥有很多优点,诸如并行性、自组织性,特别是在搜索较好解的能力.但是当开始时“信息素”不足,其搜索过程将会显现出盲目,收敛度将会大大降低.

3.2 蚁群算法的改进

1)轮盘赌算法.轮盘赌算法是一种较为常用的比例选择算法,其来源于遗传算法中选择因子的求取,主要目的是避免算法陷入局部最优解.而在蚁群算法中,第k个蚂蚁需要访问j节点,但是j节点不一定为应用式(7)求得概率最大的节点,相反j节点只能为应用式(7)求得概率值较大的集中的一个节点.所以,在应用蚁群算法求解最短路问题时,当算法运算完式(7),本文应用轮盘赌算法求解转移概率.第一步,应用式(7)计算第k个蚂蚁原有节点上访问下一个节点的最大转移概率.第二步,讲这些概率值求和后做积累概率值统计.随后依据积累概率值的大小将之分配到轮盘中对应“区域”.最后生成随机数,查看随机数落在轮盘中所对应“区域”,那么这个 “区域”将是下一个访问的节点.

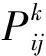
2节点：[A/(A+B+C+D+E+F),(A+B)/(A+B+C+D+E+F)]

3节点：[(A+B)/(A+B+C+D+E+F),(A+B+C)/(A+B+C+D+E+F)]

4节点：[(A+B+C)/(A+B+C+D+E+F),(A+B+C+D)/(A+B+C+D+E+F)]

5节点：[(A+B+C+D)/(A+B+C+D+E+F),(A+B+C+D+E)/(A+B+C+D+E+F)]

6节点：[(A+B+C+D+E)/(A+B+C+D+E+F),1]

最后生成在[0,1]区间的随机数,其落在那个区域哪个区域记为下一个访问的节点.

2)自适应信息素挥发系数.在传统蚁群算法中,蚂蚁常常会选择含信息量最大的路径,这样固定模式下的信息素更新,常常会造成“早熟”停滞现象.因此自适应的改变信息素蒸发系数ρ,成为解决这类问题的最佳方案.若ρ的值过大,已搜索解重新被提取的概率将增大,同理从未被选择的路径上其信息素则几乎为0,蚁群算法的全局寻优能力则大大降低；若ρ的值过小,信息素消失缓慢则将延长蚁群算法的搜索时间.所以在蚁群算法中先给定ρ以较大值,通过迭代计算式0.95ρ(t-1)来动态化减小ρ的值,ρ的值连续减小,可以提高算法的全局寻优能力.

(10)

其中ρmin为ρ的最小值.

4 配电网可靠性评估算例

本文应用IEEE-RBTSBus6主馈线F4系统如图4所示,系统参数包括：负荷点23个,隔离开关21个,

图4 含DG的RBTS Bus 6系统主馈线F4结Fig.4 Feeder F4 of RBTS-6 Bus Distribution System with DG

熔断器23个,配电变压器23台,断路器4台和DG1个.各原始数据如表2、3所示[3],设隔离开关动作时间为0.5 h,DG容量为1 MW.发生故障时,隔离开关动作率100%,熔断器熔断率100%.Ⅰ类、Ⅱ类、Ⅲ类负荷权重系数：ω1=0.47、ω2=0.32、ω3=0.21分别计算不考虑计及分布式电源和在29处分别加入1.5 MW的分布式电源的可靠性指标.

表2 设备可靠性指标

表3 线路和负荷数据

表4 算法时间

算法比较：本文分别以IEEE-RBTS2,IEEE-RBTS4,IEEE-RBTS6馈线系统结构为算例对本算法进行计算,在Matlab2010进行仿真计算，仿真见表4、5.

表5 考虑分布式电源接入后配网供电可靠性指标

5 结论

本文首先分析分布式电源接入配电网的可靠性计算模型.在积极孤岛划分的情况下使用改进蚁群算法进行最小路计算.通过与其他算法的比较,说明改进蚁群算法能够迅速的计算出最小路具有收敛速度快的特点,在现代复杂配电网的现状下,进行快速的进行可靠性评估,可以迅速的发现配电网的薄弱环节并进行治理；如果网络的可靠性较低,则可以加装继电保护装置如隔离开关等以增加配电系统的可靠性.

[1] 陈文高.配电系统可靠性实用基础[M].北京:中国电力出版社,1998:54-77．

[2] 郭永基.电力系统可靠性原理和应用[M].北京:清华大学出版社,1986.

[3] ALLAN R N,BILLINTON R,SJARIEF I,et al.A reliability test system for educational purposes:basic distribution system data and results [J].IEEE Trans on Power Systems,1991,6(2):813-820.

[4] WANG P,BILLINTON R,GOEL L.Probability distribution evaluation of distribution system reliability indices using a time sequential simulation technique[C]//2000 Canadian Conference on Electrical and Computer Engineering.Halifax,NS:Sous le patronage de IEEE Canadian Atlantic Section IEEE Canada,2000,2:760-764．

[5] BILLINTON R,WANG P.Teaching distribution system reliability evaluation using Monte Carlo simulation[J].IEEE Trans on Power Systems,1999,14(2):397-403．

[6] 杨莳百,戴景宸,孙启宏.电力系统可靠性分析基础及应用[M].北京:水利电力出版社,1986.

[7] 别朝红,王秀丽,王锡凡.电力系统可靠性评估的混合法研究[J].中国电力,2001,34(3):26-29．

[8] HEYDT G T,GRAF T J.Distribution system reliability evaluation using enhanced samples in a Monte Carlo approach[J].IEEE Trans on Power Systems,2010,25(4):2006-2008.

[9] 段海滨,王道波,朱家强,等.蚁群算法理论及应用研究的进展[J].控制与决策,2004,19(12):1321 -1326.

[10] 张鹏,郭永基.基于故障模式影响分析法的大规模配电系统可靠性评估[J].清华大学学报(自然科学版),2002(3):353-357.

[11] BILLINTON R,LI W Y.Reliability assessment of electric power systems using Monte Carlo methods [M].New York and London:Plenum Press,1994:209-254.

[12] ROLLAND E,SCHILLING D A,CURRENT J R.An efficient tabu search procedure for p-Median problem [J].European Journal of Operational Research,1996,96(2):329-342．

[13] 叶志伟,郑肇葆.蚁群算法中参数α、β、ρ设置的研究—以TSP 问题为例[J].武汉大学学报(信息科学版),2004,29 (7):597-601.

[14] DOERGO M,MANIEZZO V,COLORNT A.The ant system:optimization by a colony of coorperating Agents[J].IEEE Transactions onSystems,Man,and Cybernetics—Part B,1996，26(1):29-41.

[15] 别朝红,王秀丽,王锡凡.复杂配电系统的可靠性评估[J].西安交通大学学报,2000,34(8):9-13.

[16] 杨文宇,余健明,同向前.基于最小割集的配电系统可靠性评估算法[J].西安理工大学学报,2001,17(4):387-391．

[17] 李卫星,李志民,刘迎春.复杂辐射状配电系统的可靠性评估[J].中国电机工程学报,2003,23(3):69-79．

[18] SRINIVAS M,PATNAIK L M．Adaptive probabilities of crossover and mutation in genetic algorithm[J].IEEE transaction on systems man and cybernetics,1994,24(4):656-667．

[19] 梁才浩,段献忠.分布式发电及其对电力系统的影响[J].电力系统自动化,2001,25(6):53-56．

[20] 钱科军,袁越.分布式发电对配电网可靠性的影响研究[J].电网技术,2009,32(11):74-78.

[21] BILLINTON R,ALLAN R N.Reliability evaluation of power systems[M].London:Pitman Advanced Publishing Program,1984.

[22] GOLDBERG D E.Genetic algorithm in search,optimization and machine learning[M].Reading M A,USA:Addison-Wesley Publishing Company,Inc,1989.

[23] HUANG Junhui,Ge Shaoyun,Han Jun,et al.A diagnostic method for distribution networks based on power supply safety standards[J].Protection and Control of Modern Power Systems,2016,1(1):1-8.

[24] 王芳,李美安,段卫军.基于动态自适应蚁群算法的云计算任务调度[J].计算机应用,2013(11):3160-3162，3196.

[25] 王勋,朱建民,贺毅朝.基于遗传算法求解NPC的研究[J].河南科技学院学报(自然科学版),2014,42(6):40-45.

[26] 王军,刘三民,刘涛.基于蚁群优化的选择性集成数据流分类方法[J].长江大学学报(自然科学版),2017,23(5):37-43,85.

责任编辑：时 凌

Application of Improved Ant Colony Algorithm in Reliability Evaluation of DG Power Distribution System

WANG Chen1,LIU Hong2,ZHONG Jianwei1*,JIANG Rui1,QIN Mingliang3

(1.School of Information Engineering,Hubei University for Nationalities,Enshi 445000,China; 2.State Grid Enshi Power Supply Company,Enshi 445000,China; 3 Hubei Provincial Electric Power Company,Wuhan 430077,China )

Distributed generation (DG) access to the distribution network makes the network topology more complex.The minimum path method can be used to better analyze the distribution network in this state,and it takes into account the impact of the branch line protection,disconnector,segmented circuit breakers and can deal with the situation of whether or not there is a standby power supply or transformer.Based on the traditional ant colony algorithm,the convergence of the improved ant colony algorithm is greatly improved by using rosette and adaptive pheromone volatilization coefficient.The algorithm of IEEE RBTS Bus6 system F4 is verified by Matlab.The results show that this method can well reflect the effect of DG on the power supply reliability of the distribution network,and it can quickly analyze the topology of the distribution network and has a strong practicality.

distributed power supply;distribution network;reliability;ant colony algorithm;roulette;adaptive pheromone volatilization coefficient

2017-03-27.

国家自然科学基金项目(51177060).

王晨(1990-)，男，硕士生，主要从事配电系统可靠性问题的研究;*

钟建伟(1972-),男,硕士,教授,主要从事配电系统可靠性问题的研究.

1008-8423(2017)03-0333-06

10.13501/j.cnki.42-1569/n.2017.09.019

TM930.12

A