松弛变量法求解一类离散系统最优切换问题的全局最优解

何金凤

(重庆师范大学 数学科学学院，重庆 401331)

松弛变量法求解一类离散系统最优切换问题的全局最优解

何金凤

(重庆师范大学 数学科学学院，重庆 401331)

考虑一类离散系统的最优切换问题，最优切换问题是离散优化问题，是NP难的.采用了松弛法来求解这类问题，将原问题转化为一个容易求解的连续优化问题.在文中证明了连续优化问题与原问题的最优解是等价的，并通过数值例子验证了松弛法的快速性与有效性.

松弛变量；最优切换；切换序列

切换系统是一种特殊的混合系统，由一系列连续或离散的子系统以及协调这些子系统的切换规则所组成.在现实生活中也有很多的实际应用，例如：汽车系统、飞机和空中交通管制系统等等.本文主要讨论线性离散系统、线性型性能指标的最优控制综合问题.

当前，需要研究如何找到一个切换序列使目标函数值达到最优，在切换系统的最优切换问题中已经受到了广泛关注，关于这个问题的研究有许多理论和计算结果在相应的文献中都能找到.文献[1]介绍了一般的混合系统模型，文献[2]提出了求解混合系统最优控制问题的极大化原则.文献[3-12]提出了梯度法，并且利用这种方法找到最优切换序列.

本文考虑线性目标函数在离散时间切换系统中的最优切换序列，其中在每个时间点仅仅只有一个活动的子系统.按照这个线性子系统和目标函数的结构特征，在状态方程中加入松弛变量，这就是松弛法，它是解决最优控制问题的一种新方法.

1 问题描述

本文主要考虑一个离散时间切换问题，它有N个子系统如下：

x(t+1)=Ai(t)x(t),t∈I,i=1,2,…,N

(1)

初始条件为x(0)=x0，其中，

x(t)=(x1(t),x2(t),…,xN(t))T∈Rn,I={0,1,…,T-1}.

假设切换系统的一个切换顺序可以用函数σ(t)来表示，对于任意t∈I，有σ(t)∈{1,2,…,N}，当时σ(t)=i，表示在t时刻采用第i个子系统.

于是，系统就变为x(t+1)=Aσ(t)(t)x(t)，那么最优切换问题表述如下：

问题1 寻找一个σ(t)函数，使得目标函数

(2)

达到最小值.

通过上面的问题表述，可以看出σ(t)是一个离散变量，问题1是一个离散优化问题.由于对于每一个t,σ(t)有N种取法，所以σ(t)的所有可行解有NT个，它随着T的增大而指数性增大，因此，它是NP难问题，求解非常困难.

2 问题求解

离散优化问题一般需要穷举法才能得到全局最优解.本文主要采用松弛法，将问题1转化为连续优化问题并求出其全局最优解.为此，引入松弛变量

wi(t),t∈I

(3)

表示第i个子系统在t时刻的权重函数，它需要满足以下条件：

那么，将权重函数作用于每一个子系统后，切换系统转化为以下形式:

(4)

初始条件:

x(0)=x0

(5)

其中:令w=(w(0),w(1)，…，w(T-1)),w(t)=(w1(t),w2(t),…,wN(t))T定义集合：

那么∀t∈I，w(t)∈W，因此w∈W×W×…×W=WT.

问题2 寻找一个w∈WT，使得目标函数:

(6)

达到最小值.

问题2是一个离散系统的最优控制问题，其中w(t)是控制函数.由于w(t)是连续变量，则问题2可以转化为一个连续优化问题，对它的求解就变得非常容易了.

接下来，将通过求解连续优化问题2，从而得出问题1的全局最优解.

引理1 若u=(u(1),u(2),…,u(N))∈W，并且∀i，有u(i)等于0或1，那么有且只有一个i∈{1,2,…,N}，使得u(i)=1,u(j)=0，i≠j.

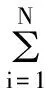
根据引理1，可以得到下面的定理.

定理1 问题2存在一个最优解w*的取值是0或者1，即w*等于0或者1，∀t∈I，i∈{1,2,…,N}.

证明 通过状态方程(4)和初始条件(5)，发现这些状态方程都是关于变量w的函数.把状态方程带入问题2的目标函数中，可以表示为：

(7)

当时t≥1，要求出最优解，则需要对函数(7)进行相应的归纳整理.假设找不到一个最优解w*在t1时刻的值不是0或1，那么把t≠t1的变量固定，则此时函数中的变量就只有w(t1)，从而目标函数中的变量就从N×T个变为只有N个，分别是w1(t1)，w2(t1)，…，wN(t1).由于目标函数(7)中关于wi(t)的项都是线性的，把目标函数(7)归纳整理总能得到这样的模型:

J(w(t1))=a1w1(t1)+a2w2(t1)+…+aNwN(t1)+c

(8)

这是一个线性规划模型，可以求解这个问题得出最优的w(t1)，并且w(t1)是在边界上，即它的取值是0或1，于是与假设矛盾.因此，肯定能找到一个最优解w*使得它的取值为0或1，证毕.

通过定理1的证明可知，引入松弛变量把问题变为连续的线性规划问题是可行的，并且还能求出最优的切换序列.

定理2 问题(2)至少存在一个最优解为问题1的最优解.

3 示例分析

将列举两个例子，分别采用穷举法和松弛法进行求解，然后分析比较这两种方法的结果，计算是在Matlab 2007中完成的.在下面的例子中都是考虑N=4的离散时间切换系统问题，也就是有4个子系统，时间T=10.

例1 考虑以下子系统的切换：

设初始条件以及p0为:x0=(1，1，0)T,p0=(1，1，1)T.

表1 切换序列及相应的目标函数值

首先，利用穷举法进行求解，不难发现穷举法需要搜索的可行解是410个，并且运行结果大约为85.644s，其中目标函数值为1 811，能得到最优的切换顺序为w={4,2,4,2,4,2,4,2,4,2}. 然而，如果应用松弛法求解，能够得到相同的目标函数值，以及最优的切换序列，所花费的时间仅仅需要1.794s.因此，通过以上两种方法的求解，松弛法明显比穷举法有效.其中运用松弛法搜索的部分序列在表1中给出.

例2 考虑以下子系统的切换:

设初始条件和p0为:x0=(1，-1，0)T,p0=(1，1，1)T.

表2 切换序列及相应的目标函数值

通过Matlab软件，使用松弛法和穷举法计算出的最优切换序列为w=(4,4,4,2,1,1,1,1,1,1)，其中松弛法运行时间为1.42s，目标函数值为-169.971.而运用穷举法计算出目标函数值也是-169.971，所花的时间为122.336s，因此，松弛法在时间和迭代次数上都给问题的求解带来了很大的方便.其中运用松弛法搜索的部分序列在表2中给出.

4 结论

本文主要考虑了离散时间切换系统的最优切换问题，其中，子系统和目标函数都是线性的.并且提出运用松弛法求解离散时间切换系统问题，表明通过把离散时间切换问题转化为连续的优化问题，运用松弛法求解最优切换序列是可行的.通过用松弛法与一般的穷举法进行比较，发现运用松弛法求解这一类问题非常有效.

[1] PICCOLI B.Hybrid systems and optimal control[J].Proc of the 37th IEEE Conference on Decision and Control,1998(1):13-18.

[2] SUSSMANN H J.Amaximum priciple for hybrid optimal control problems[J].Proc of the 38th IEEE Conference on Decision and Control,1999(1):425-430.

[3] XU X,ANTSAKLIS P J.Optimal control of switched autonomous systems[J].Proc of the 41nd IEEE Conference on Decision and Control,2002,4:4 401-4 406.

[4] EGERSTEDT M,WARDI Y,DELMOTTE F.Optimal control of switching times in switched dynamical systems[J].Proc of the 42nd IEEE Conference on Decision and Control,2002,3:2 138-2 143.

[5] EGERSTEDT M,WARDI Y,AXELSSON H.Transition-time optimization for switched-mode dynamical systems[J].IEEE Transactions on Automatic Control,2006,51(1):110-115.

[6] XU X,ANTSAKLIS P J.Optimal control of switched systems based on parameterization of the switching instants[J].IEEE Transactions on Automatic Control,2004,49:2-16.

[7] LI R,TEO K L,WONG K H,et al.Control parametrization enhancing transform for optimalcontrolof switched systems[J].Mathematical and Conputer Modelling,2006,43(11/12):1 393-1 403.

[8] LEE H W J,TEO K L,JENNING L S.Control parametrization enhancing techniques for optimal discrete-valued control problems[J].Automatica,1999,35:1 401-1 407.

[9] TEO K L,JENNING L S,LEE H W J,et al.The Control parametrization enhancing transform for constrained optimal control problems[J].Journal of Australian Mathematical Society,Series B,1999,40:314-335.

[10] BENGEA S C,DECARLO R A.Optimal control of switching systems[J].Automatica,2005,41:11-27.

[11] AXELSSON H,WARDI Y,EGERSTEDT M,et al.Gradient descent approach to optiomal mode scheduling in hybrid dynamical systems[J].Journal of Optimization Theory and Applications,2008,136(2):167-186.

[12] WARDI Y,EGERSTEDT M.Algorithm for optimal mode scheduling in switched systems[J].American Control Conference,2012，41:4 546-4 551.

责任编辑：高 山

On the Global Optimal Solution for the Optimal Switching Problem of a Class of Discrete Switched Systems

HE Jinfeng

( School of Mathematical Sciences,Chongqing Normal University,Chongqing 401331,China)

In this paper,we consider a class of optimal switching problem in discrete time.The optimal switching problem is a discrete optimization problem,which is NP-hard.We apply the relaxation method to solve a class of optimal switching problem,where the problem is transformed into a continuous optimization problem,which is easy to find the solution.We prove that the optimal solution of continuous optimization problem is equivalent to that of original problem.Numerical examples are provided to show that the relaxation method is efficient and effective.

relaxation variable; optimal switching; switching sequence

2017-03-16.

国家自然科学基金项目(61473326)；重庆市自然科学基金项目(cstc2017jcyjAX0161);重庆师范大学研究生科研创新项目(YKC17016).

何金凤(1990-)，女，硕士生，主要从事最优控制的研究.

1008-8423(2017)03-0282-04

10.13501/j.cnki.42-1569/n.2017.09.008

O232

A