Buck电路输出电流的神经网络PID控制

田家俊，钟建伟

(1.国网恩施供电公司,湖北 恩施 445000；2.湖北民族学院 信息工程学院,湖北 恩施 445000)

Buck电路输出电流的神经网络PID控制

田家俊1，钟建伟2

(1.国网恩施供电公司,湖北 恩施 445000；2.湖北民族学院 信息工程学院,湖北 恩施 445000)

简述了降压斩波电路的电路模型,从其原理上解释其非线性输出的原因.其次,描述了传统控制的局限性和神经网络的研究现状,介绍了神经网络的特征和功能.再者,通过神经网络的模型,对BP算法进行了数学公式推导,给出了BP算法的详细思路和具体过程,采用Matlab软件编程实现BP神经网络算法,并将算法训练后的BP神经网络运用到非线性函数的逼近中去.最后,使用Matlab软件下的Simulink模块搭建了降压斩波电路,再分别搭建传统PID控制和神经网络PID控制的结构模型对其进行控制仿真,得到相应的输出电流电压仿真结果图.仿真结果表明,BP神经网络控制器具有更好的控制效果,相比较闭环PID控制器,能够有效克服经典PID控制器在被控对象具有非线性、时变不确定性和难以建立精确的数学模型时,出现的控制结构复杂、参数整定不良和性能欠佳等缺点.

降压斩波电路；神经网络；PID控制

1 引言

1.1 传统控制理论的局限性

控制理论经历了现代控制理论和大理论两个重要的发展阶段.在严格精确的数学模型基础之上,对系统分析、综合和设计的控制,由于很大程度的依赖于精确数学模型,使其应用领域受到了很大程度的限制.而科学技术和信息化高速发展的今天,人们要求实现大规模、复杂和不确定性自动控制系统,由于控制对象的严重非线性,数学模型的不确定性,系统工作点变化剧烈等因素,设计这些系统时,必须提出并遵循一些比较苛刻的假设,而这些假设在应用中往往与实际不相吻合,一般无法获得精确的数学模型,传统控制存在着难以弥补的严重缺陷[1-3].这就促使人们提出了新的控制技术和方法.

1.2 传统PID控制的特点

传统PID控制是历史悠久、应用广泛的经典控制方法,虽然后来出现了很多新的控制方法,但是大多数都是在原有的传统PID控制方法的基础上的一些改进.目前正在运行的控制回路中,90%以上还是PID控制器.在PID控制器中,比例部分产生与偏差值成正比的输出信号,以便消除偏差；积分部分产生与偏差积分成正比的输出信号,可以消除系统的静态误差；微分部分产生与偏差变化率成正比的输出信号,以便缩短过渡过程时间,减少超调量,加快控制器的调节速率.如果在工作者经验的基础上,通过调整这三个部分的大小,得到恰当的系数参数,便可以使PID控制器得到快速、平稳和准确的调节效果.

因此,PID控制器的设计关键问题是如何选取恰当的比例、积分、微分系数,而这些参数的整定的困难使得PID控制器的应用受到限制.实际上,PID控制规律是一种线性的控制规律,这就使得它具有了传统控制理念中通用弱点,即仅在简单的线性单变量控制系统中有较好的控制效果,而在复杂控制系统中效果难以达到控制要求.

1.3 神经网络和PID控制相结合的研究现状

图1 神经元网络和PID控制现有结合方式一Fig.1 Neural network and PID control of the existing combination of a way

1)采用神经元确定PID参数.在原来传统的PID控制器的基础上,加入一个或多个神经元网络模型.利用神经元的自适应学习功能,可以调整和确定PID参数,其结构如图1所示.

此控制器分为虚线内PID控制部分和神经元网络两个部分:虚线内PID部分,是按照传统PID控制器的结构来构成的,对系统偏差信号进行比例、积分和微分处理,通过加权相加重值比例、积分和微分系数；神经网络部分,一般采用多层前向网络,可以根据系统的输入和输出的信息,通过反复的学习和调整所需的PID参数[4-5].

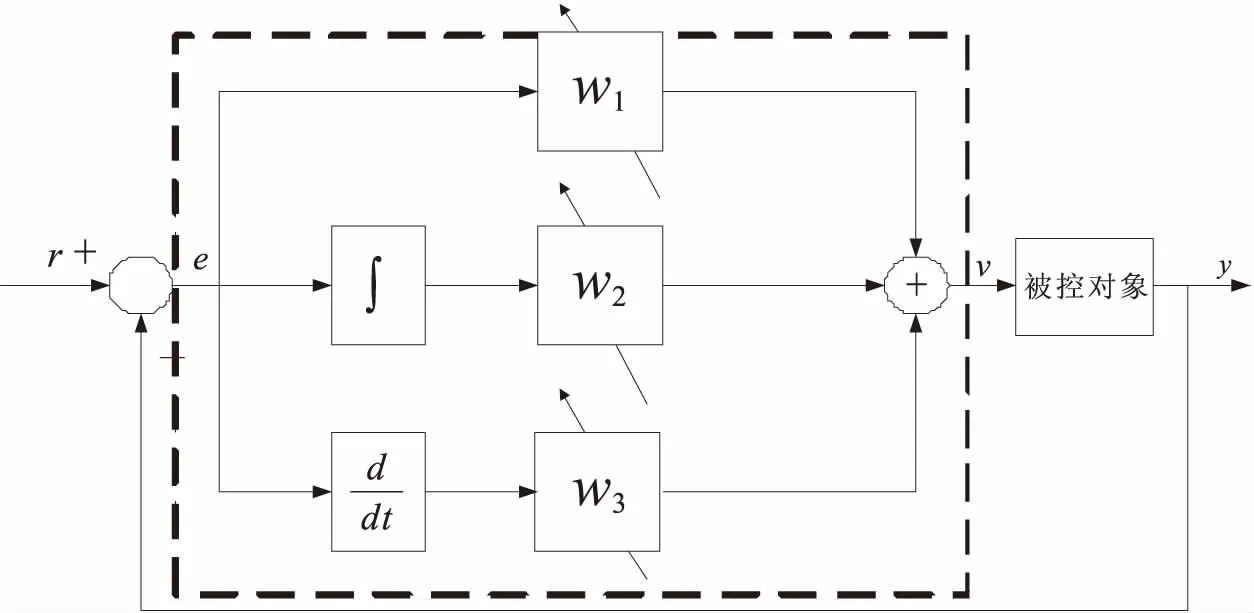
图2 神经元网络和PID控制现有结合方式二Fig.2 Neural network and PID control of the existing combination of two

2)单神经元结构PID控制器.单神经元结构PID控制器的结构模型如图2所示.虚线内表示的是单神经元网络结构.它系统中的比例、积分和微分的系数是根据输入信号的采样[6-9],分别对系统的比例、积分和微分的偏差,通过不断整定单神经元的输入权重值一一对应比例、积分和微分系数[10-11].

2 基于神经网络的PID控制器

2.1 常规PID控制的Simulink仿真模型

在Matlab软件仿真中,设计一个简单的对象模型,并假设在对象模型中含有纯滞后环节,通过Simulink模块来模拟该系统.加入了输入和外加扰动信号,Simulink模型的结构如图3所示.其中用来表示PID控制器的数学表示为:

(1)

在PID模块中的参数可以由实际PID控制器参数直接计算出来:

p=Kp,I=Kp/Ti,D=Kp×Td,N=N/Td

2.2 神经元PID控制器的Simulink仿真模型

由仿真结果(见图4，5)可知,神经网络无超调量,而传统PID控制器超调量为40%左右.由此可以得出结论:在不增加算法复杂性的前提下,神经网络控制器可以提高收敛速度,并且可以达到全局最优.神经网络控制器是不需要精确数学模型的无模型控制.能有效地提高系统的实用性和鲁棒性,可以实现在线整定控制参数,具有很强的自适应和自学习能力.

图3 传统PID 控制器结构图 图4 传统PID 和神经网络PID 控制器Simulink 模型

Fig．3 Traditional PID controller structure diagram Fig．4 Traditional PID and neural network PID controller simulink model

图5 传统PID和神经网络PID控制器波形Fig.5 Traditional PID and Neural Network PID Controller Waveforms

3 基于神经网络PID零电流准谐振BUCK变换器

使用Matlab中的Simulink模块来建立零电流开关准谐振BUCK变换器的仿真电路模型,取输入电压200 V,电感L=40μF,电容C=0.03μF,负载R=3.8Ω.建立仿真模型如图6所示.

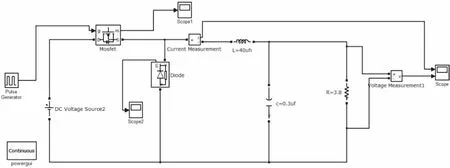
图6 零电流准谐振BUCK型DC-DC变换器仿真模型Fig.6 Simulation Model of Zero-current Quasi-resonant BUCK Type DC-DC Converter

1)仿真实验1:ZCS-QR BUCK变换器的开环控制.在开环控制系统中,不加入任何控制器,并且由一个脉冲信号发生器来触发软开关功率变换器中的MOSFET管.通过设定脉冲信号发生器的参数,就可以来调节功率开关管的开通和关断的时间,得到系统相应的输出电压或电流.在这里选择脉冲信号发生器的脉冲信号周期为0.000 2 s,占空比为50%.开环控制的结构图如图6所示,它在t=0.1 、0.01 s内的电流电压仿真如下图7、8所示.

图7 ZCS-QR BUCK变换器开环条件下t=0.1 s内输出电流电压波形Fig.7 ZCS-QR BUCK converter under open-loop conditions t=0.1 s within the output current voltage waveform

图8 ZCS-QR BUCK变换器开环条件下t=0.01 s内输出电流电压波形Fig.8 ZCS-QR BUCK converter under open-loop conditions t=0.01 s within the output current voltage waveform

从仿真结果可以看出,在没有外界干扰的开环控制中,可以通过手动调整触发信号的占空比,就可以达到较好的控制效果.但是,这种没有反馈环节控制方式,其灵活性很差,超调量较大.当系统的负载发生变化时,整个系统是不具有调节性的,而且输出电压或电流变化很大,不具有控制的稳定性.然而对于实际应用中,开环控制易于受到外界如电压波动、负载扰动、电磁等各类干扰,这就难以达到理想控制的结果.

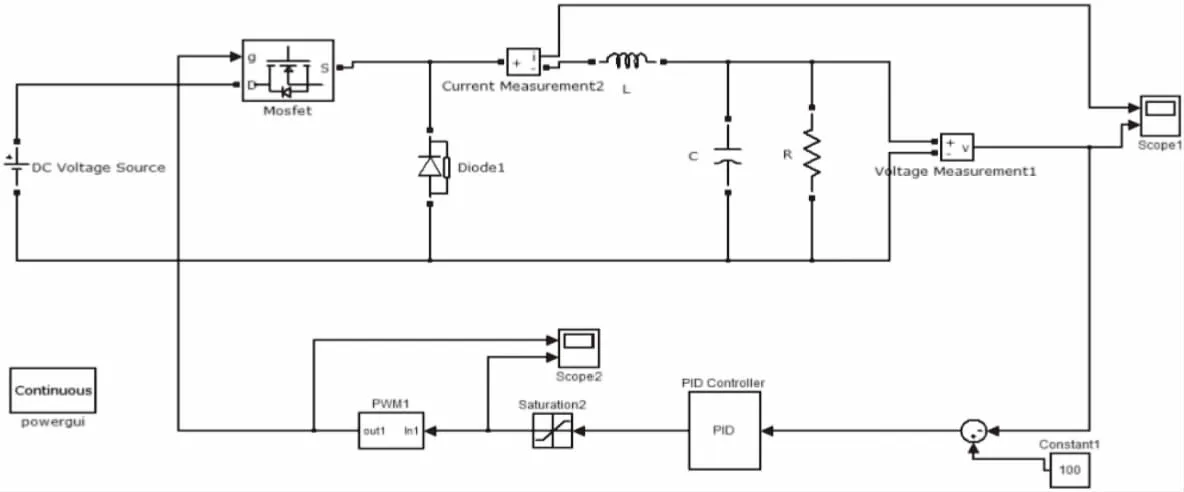
图9 ZCS-QR BUCK变换器闭环传统PID控制仿真模型Fig.9 Simulation model of closed-loop traditional PID control for ZCS-QR BUCK converter

2)仿真实验2:ZCS-QR BUCK变换器的闭环传统 PID控制.通过采用输出信号反馈环节,将传统 PID控制器作用到它的输入端就构成了闭环控制,电路中的参数同图6中的电路参数相同,其仿真电路模型如图9所示.

从图9中可以看出,采用传统PID控制器比其他控制设计方法相对简单,还能有更好的控制效果.但是,比例、积分、微分的系数很难调整到最佳,这需要有丰富经验的长期工作者来进行调整到最优值.

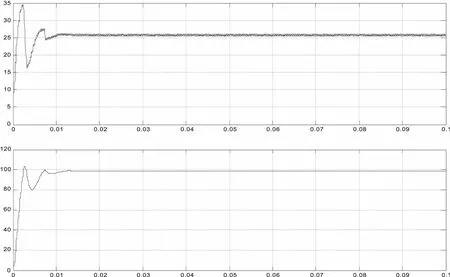
图10 传统PID控制器输出电流电压波形Fig.10 Traditional PID controller output current voltage waveform

在稳态情况下,在t=0.009 s左右达到稳定值,PID控制与开环控制的相差不是很大,电压纹波很小,非常平稳.在暂态过程的动态响应中,PID控制比开环控制的输出电压的超调量小的多.因此,传统PID控制也可以达到很好的控制效果.

3)仿真实验3:ZCS-QR BUCK变换器的PID神经网络控制.用PID神经网络部分来代替图9中的PID控制器部分,形成了PID神经网络的控制方式,其中PID神经网络控制器的具体结构前面章节已经详细介绍,这里是采用基于s函数的BP神经网络PID控制器.电路中参数不变,其仿真电路模型如图10所示.

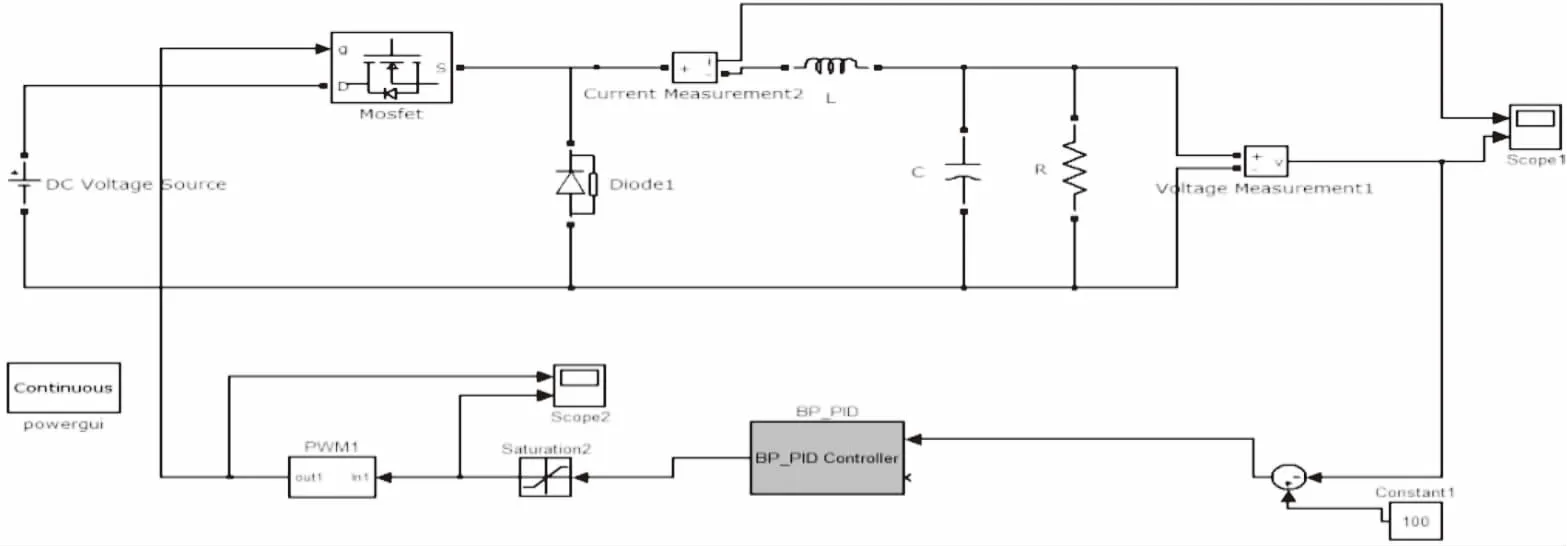
图11 ZCS-QR BUCK变换器闭环神经网络PID控制仿真模型Fig.11 ZCS-QR BUCK converter closed loop neural network PID control simulation model

如图11所示,从仿真图可以看出,在t=0.01 s以后稳态情况下,神经网络PID控制器的输出电压非常稳定,纹波很小,系统稳态误差较小.在t=0～0.01 s暂态情况下,超调量非常小,上升时间较短,系统响应速度快,因此,采用PID神经网络控制器比其他控制器的控制效果好.但是神经网络PID控制有一个学习训练的过程(从图上看t=0.005 s左右),会在一段时间后才能达到稳定值.

4 结论

图12 神经网络PID控制器输出电流电压波形Fig.12 Neural network PID controller output current voltage waveform

在BP神经网络理论和传统PID控制技术的科学基础下,提出了一种基于BP神经网络的新型PID控制方法:将其应用于Buck电路闭环系统的控制,并与传统的PID控制的效果进行比较.仿真结果表明,训练后的BP神经网络具有较强的自我学习和自我修正能力,改善系统控制的优越性,从而进一步提高了控制器的性能.下一步何将基于BP神经网络的PID控制器应用到实际的控制系统中去,并针对不同特性(如非最小相位系统、不稳定系统等)的系统时进行研究,以期达到较好的控制效果.

[1] 蒋宗礼.人工神经网络导论[M].北京:高等教育出版社,2001:15-90.

[2] 陈桦,程云艳.BP神经网络算法的改进及在MATLAB中的实现[J].陕西科技大学学报,2004,22:45-47.

[3] 闻新,周露,王丹力,等.MATLAB神经网络应用设计[M].北京:科学出版社,2001:10-50.

[4] DE Paor A M，MALLEY M O.Controllers of Ziegler Nichols type for unstable processes [J].International Journal of Control,1989,49(4),1273-1284.

[5] 周开利,康耀红.神经网络模型及其MATLAB仿真程序设计[M].北京：清华大学出版社，2006:10-43.

[6] SHU H L,PI Y G.PID neural networks for time-delay systems[J].Computers and Chemical Engineering,2000,24:859-862.

[7] 牛建军,吴伟,陈国定.基于神经网络自整定PID控制策略及其仿真[J].系统仿真学报,2005,17(6):1425-1427.

[8] 丛爽.神经网络、模糊系统及其在运动控制中的应用[M].合肥:中国科学技术大学出版社,2001:20-31.

[9] V Etxebarria.Adaptive Control of Discrete Systems Using Neural Networks[J].IEE Proc Pt D,Control Theory and Application,1994,141(4):209-215.

[10] 郝万君,乔焰辉,李泽,等.基于模糊模型的一类不确定非线性系统协调优化控制[J].苏州科技学院学报(自然科学版),2015,32(4):40-45,2.

[11] 张同君.BP神经网络在水利发电控制系统中的应用[J].河北科技师范学院学报,2016,30(1):62-67.

责任编辑：时 凌

Neural Network PID Control of Output Current of Buck Circuit

TIAN Jiajun1,ZHONG Jianwei2

(1.State Grid Enshi Power Supply Company,Enshi 445000,China；2.School of Information Engineering,Hubei University for Nationalities,Enshi 445000,China)

This paper introduces briefly the circuit model of buck chopper circuit and theoretically explains the reason for its nonlinear output.Secondly,it describes the limitations of traditional control and the research status of the neural network,and introduces the characteristics and function of the neural network.Moreover,through the model of neural network,it makes the mathematical formula derivation for BP algorithm and gives a detailed idea and the specific process of BP algorithm.Matlab software programming is used to realize BP neural network algorithm,and the BP neural network of the algorithm after training is applied to nonlinear function approximation.Finally,the Simulink module of Matlab software is used to build the buck chopper circuit,then the structure models of traditional PID control and neural network PID control are respectively set up for control simulation,and the simulation results of output current and voltage are obtained.The simulation results show that the BP neural network controller has better control effect.Compared with the closed loop PID controller,the BP neural network controller can effectively overcome such disadvantages as complex control structure,poor parameter setting and poor performance of the traditional PID controller in the case of non-linear controlled object,time-varying uncertainty and difficulty in establishing an accurate mathematical model.

buck chopper;neural network;PID control

2017-02-22.

湖北省自然科学基金计划项目(2013CFC125).

田家俊(1986-),男(土家族),主要从事电力系统运行与控制的研究；*

钟建伟(1972-),男(土家族),硕士，教授,主要从事电力系统运行与控制的研究.

1008-8423(2017)03-0347-05

10.13501/j.cnki.42-1569/n.2017.09.022

TM762

A