线性规划模型无穷多最优解的一种检验方法

余胜平,吴庆华,刘 坤,陈加毫

(湖北工程学院 数学与统计学院 湖北 孝感 432000)

线性规划模型无穷多最优解的一种检验方法

余胜平,吴庆华,刘 坤,陈加毫

(湖北工程学院 数学与统计学院 湖北 孝感 432000)

针对线性规划模型有解时的两种情形(唯一最优解和无穷多最优解),提出了一种判别最优解是否唯一的方法.该方法通过一系列线性规划模型,可计算出所有决策变量的取值范围.根据这些取值范围,判断最优解是否唯一.进一步给出了一种策略,可确定原问题的一个唯一最优解.最后,数值实验验证了该方法的可行性和有效性.

线性规划;无穷多最优解;唯一最优解

线性规划作为运筹学的一个分支,在经济、管理、工程、技术等领域中有着广泛的应用,许多实际问题都可通过线性规划模型来求解.如:决策分析中方案的分类[1]、数据包络分析中决策单元的比较和排序[2]、模糊矩阵对策[3],等等.通常,当线性规划模型有解时,线性规划的最优解可分为唯一最优解和无穷多最优解两种情形.线性规划的无穷多个最优解一方面给决策人提供了多种最优方案,增加了选择的灵活性；另一方面,却给计算结果带来了不确定性,需要进一步考虑其他因素,以确定合适的最优解.一些研究者研究了线性规划有无穷多最优解的条件以及无穷最优解的表示形式.如文献[4]根据凸多面体的表示定理,给出了标准型线性规划最优解的一般表达式和计算全部最优解的步骤.文献[5]则给出了线性规划有无穷多最优解的判别方法和表达式.然而,这些方法都只是从理论上进行分析,无法利用现有的软件和算法在求解线性规划时,直接判断线性规划最优解是否唯一.另外,在计算机软件和算法普遍使用的今天,提出了许多算法求解线性规划[6-8],但这些软件和算法一般只能得到一个最优解,当线性规划模型存在无穷多最优解时,通常不同的软件和算法得到的最优解有可能不同.文献[9]虽然利用Excel软件敏感性报告中非基变量检验数值来判断是否唯一,但该方法并不适用决策变量较多时的情形.为了解决这一问题,本文利用Matlab软件给出了一种判别线性规划模型最优解是否唯一的方法,并且通过求解一系列相同约束条件的线性规划模型,可得到每个决策变量的取值范围.当线性规划有无穷多最优解时,提出了一种策略确定原模型的最优解,此最优解在该策略下是唯一的.

1 线性规划模型的基础知识

考虑如下的线性规划模型：

(1)

其中:x=(x1,x2,…,xn)T为决策变量;c=(c1,c2,…,cn)T是变量的价值系数;A和Aeq分别为不等式和等式约束系数矩阵;b、beq是不等式和等式约束条件对应的右端项向量,LB,UB分别为决策变量x的上、下界向量.此线性规划模型的可行域记为S1,即S1={x|Ax≤b,Aeqx=beq,LB≤x≤UB}

线性规划模型的一个典型特征是目标函数和约束函数均为线性函数,因此,线性规划模型具有一些良好的性质.如:当可行域S1非空时,S1一定为凸集；线性规划模型是一种特殊的凸规划模型,其局部最优解一定是全局最优解,最优值是唯一确定的,等等.然而,当可行域S1非空时,线性规划模型的最优解分为无界解、唯一解或无穷多最优解三种情形.而现有的优化算法或软件一般只能确定一个最优解.当线性规划模型有无穷多最优解时,通常,不同软件得到的最优解也可能不同.本文利用优化软件检验线性规划模型是否为唯一解或无穷多最优解.

2 线性规划模型唯一解或无穷多最优解的检验方法

假设模型(1)的最优值为z*,最优解为x*,一般来说,当可行域非空时,x*是唯一解或无穷多最优解,z*是唯一确定的.记N={1,2,…,n},为了得到每个决策变量xi(i∈N)的最大值或最小值,可构造如下的模型(2)和模型(3),它们具有相同的可行域.

和

对于模型(1),有如下的结论:

定理1 模型(1)的最优解一定是模型(2)和(3)的可行解.

证明 假设模型(2)和(3)的可行域为S2,由于x*为模型(1)的最优解,则x*∈S1,且CTx*=z*.

从而x*∈S2,故模型(1)的最优解是模型(2)和(3)的可行解.

定理1说明了当模型(1)存在最优解时,模型(2)和(3)一定是可行的.

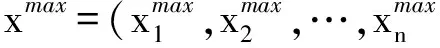
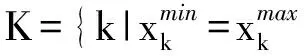
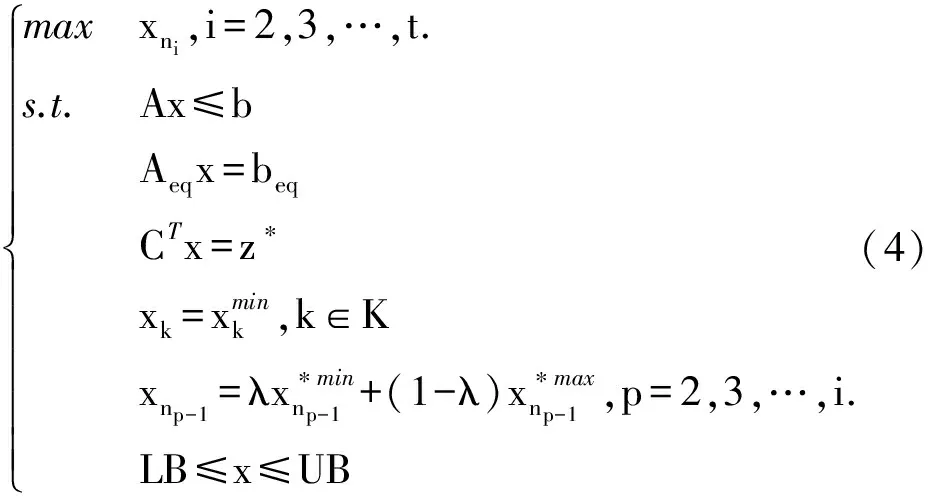
和

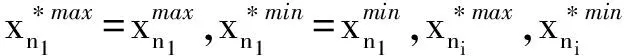
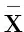
第1步:求解模型(1),得到最优值z*；

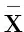
3 算例

(6)

其中c=(0.079 8,0.073 5,0.065 7,0,0,0)T,

11

利用Matlab软件计算,可得到模型(1)的最优值为z*=1,在模型(1)中增加约束条件CTx=1,依次求解模型(2)和(3),得到所有变量的取值范围见表1.

表1 决策变量的取值范围

决策变量的最大取值和最小取值并不完全相同,根据定理2,则模型(1)有无穷多最优解.给定不同的值,依次求解模型(4)和(5),可得到其对应的唯一最优解,这些解均为模型(1)的最优解,结果见表2.

表2 不同的值时模型(1)的最优解

4 小结

线性规划模型有无穷多最优解时给决策人提供了多种解决方案,增加了选择的灵活性,同时也给计算结果带来了不确定性,本文利用优化软件给出了一种判别方法,可得到所有决策变量的取值范围.也提出了一种策略得到原线性规划问题的一个最优解,该解在此策略下是唯一确定的.本文方法为决策人利用软件判断线性规划最优解是否唯一,以及确定唯一的最优解提供了一种思路.

[1] ZOPOUNIDIS C,DOUMPOS M.Multicriteria classification and sorting methods:A literature review[J].European Journal of Operational Research,2002,138(2):229-246.

[2] LOTFI F H,JAHANSHAHLOO G R,Khodabakhshi M,et al.A Review of Ranking Models in Data Envelopment Analysis[J].Journal of Applied Mathematics,2013,2013(15):3600-3611.

[3] 杨洁,李登峰.求解梯形模糊矩阵对策的线性规划方法[J].控制与决策,2015,30(7):1219-1226.

[4] 薛声家,左小德.确定线性规划全部最优解的方法[J].数学的实践与认识,2005,35(1):101-105.

[5] 徐永仁,张绍斌,董绍斌.线性规划问题无穷多最优解的判别及表达式[J].哈尔滨工业大学学报,2004,36(1):102-105.

[6] 雍龙泉.求解线性规划的几种方法[J].江西科学,2007,25(2):202-205.

[7] KHOBRAGADE N W,VAIDYA N V,LAMBA N K.Approximation algorithm for optimal solution to the linear programming problem[J].International Journal of Mathematics in Operational Research,2014,6(2):139-154.

[8] 曾国斌.线性规划问题的相关算法研究[J].赤峰学院学报(自然科学版),2014,30(5)(下):1-2.

[9] 李如兵,宗凤喜.Excel中线性规划问题无穷多最优解情况的判别[J].曲靖师范学院学报,2014,33(3):12-14.

责任编辑：时 凌

A Method to Test the Multiple Alternative Optimal Solutions for Linear Programming Model

YU Shengping,WU Qinghua,LIU Kun,CHEN Jiahao

(School of Mathematics and Statistics,Hubei Engineering University,Xiaogan 432000,China)

If there exists at least a solution for the linear programming model,the solutions can usually be divided into the unique optimal solution and multiple alternative optimal solutions.In this paper,a method is presented to justify whether the solution for linear programming is unique or not.The ranges of all decision variables can be calculated to test the uniqueness of optimal solution using a series of linear programming models.A strategy is provided to determine the final solution,which can be proved to be unique and optimal solution for the original linear programming model.Finally,a numerical example is given to illustrate the feasibility and effectiveness of the proposed method.

linear programming;alternative optimal solutions;unique optimal solution

2017-05-21.

国家自然科学基金项目(11601138);湖北省教育厅科学研究计划项目(B2017168)；湖北省大学生创新创业训练计划项目(201710528002).

余胜平(1980-),女,硕士,讲师,主要从事最优化理论与方法的研究.

1008-8423(2017)03-0278-04

10.13501/j.cnki.42-1569/n.2017.09.007

O221.1

A