一种新型电磁作动器电磁力影响参数分析*

2017-09-12宁一高张仰成

振动、测试与诊断 2017年4期

关键词：匝数作动器电磁力

宁一高 ,石勇 ,张仰成

(1.哈尔滨工程大学动力与能源工程学院哈尔滨，150001)(2.北京卫星制造厂北京，100190)

一种新型电磁作动器电磁力影响参数分析*

宁一高1,石勇1,张仰成2

(1.哈尔滨工程大学动力与能源工程学院哈尔滨，150001)(2.北京卫星制造厂北京，100190)

针对各参数对一种新型电磁作动器电磁力影响机理的问题，利用ANSYS软件建立了该电磁作动器的电磁力仿真计算模型，并对加工好的样机电磁力进行试验测量。结果表明，仿真计算结果能够与试验数据很好的吻合，最大相对误差仅为11.6%，从而验证了仿真模型的有效性。利用该仿真模型分析了齿高、线圈匝数、齿数、气隙、衔铁厚度和轭铁厚度等参数对电磁力的影响，揭示了其影响机理,为这种电磁作动器的进一步优化设计奠定了基础，对类似结构的电磁执行器的设计具有一定的参考价值。

电磁作动器；电磁力；仿真计算；试验测量；影响参数

引言

动力机械是舰船的主要振动噪声源之一，其严重损害船员的身心健康，影响舰船的战斗能力。采用隔振装置将动力设备弹性安装，能够有效减小传递到船体结构上的振动，是舰船减振降噪的最重要技术手段之一[1]。半主动隔振系统与被动式隔振系统相比，具有能适应外扰频率变化，有效隔离低频振动的优点；与主动隔振系统相比，需要的附加能源少、价格低，且整个系统比较简单、可靠性高[2]。

作动器是隔振系统的关键部件，对隔振效果起到至关重要的作用。半主动隔振系统的作动器根据原理主要分为可变阻尼式和可变刚度式两大类，已经得到了较为广泛的研究。Guglielmino等[3]对液压驱动摩擦式阻尼器进行了研究。Suda等[4]对电磁阻尼器进行了研究。文献[5-6]对磁流变液阻尼器进行了研究。李锐等[7]以短型浮置板轨道隔振为例，对磁流变隔振器阻尼参数进行了优化研究。文献[8]对智能弹簧进行了研究。周卓亮[9]利用齿形结构的电磁弹簧，设计了可变刚度隔振器，并进行了初步的半主动隔振试验。石勇等[10]设计了一种新型变齿距齿宽电磁作动器，相比定齿距齿宽电磁作动器具有线性度好、易控制等优点。

电磁力是电磁作动器的最重要性能指标之一。针对变齿距齿宽电磁作动器涉及机、电、磁多物理场耦合导致其各参数对电磁力的影响机理还不清楚的问题，笔者采用ANSYS软件建立了电磁作动器的仿真模型，并对该模型进行了试验验证。利用该仿真模型分析了各参数对电磁力的影响规律，并揭示了相应的影响机理。

1 新型电磁作动器结构和工作原理

以图1所示的单自由度隔振系统为例，设其沿垂直方向受到的外扰力为F=F0sin(ωt),传至地面的力的幅值为FT，则力的传递率为

(1)

由式(1)可以看出，在不同的外扰频率ω下，恰当地改变系统的刚度k、阻尼c或质量m都可以降低力的传递率，从而改善隔振效果。

图1 单自由度隔振系统Fig.1 Single-degree-of-freedom vibration-isolation system

笔者研究的新型电磁作动器是通过在不同工况下改变系统刚度来实现良好隔振效果的，其结构如图2所示，它是根据反应式步进电机的原理工作的。可以看出，在壳体、法兰和衔铁相对的工作面上开有变齿宽的小齿，相对的齿面间存在一定大小的气隙。当不发生振动时，壳体、法兰上的齿和衔铁上的齿是对齐的，作动器对外不产生作用力。当发生振动时，衔铁上的齿与壳体、法兰上的齿发生相对位移，作动器就会对外产生轴向作用力，力的大小与相对位移的大小在一定范围内基本成线性关系。通过改变线圈绕组上驱动电流的大小，可以改变作动器的位移-力特性曲线的斜率，即改变系统的刚度，从而实现良好的隔振效果。

1-壳体；2-线圈架；3-法兰；4-轴承端盖；5-直线轴承；6-主轴；7-弹性圆柱销；8-衔铁；9，10-螺栓图2 新型电磁作动器结构图Fig.2 Schematic of novel electromagnetic actuator

2 仿真模型的建立

2.1 有限元计算的数学原理

求解电磁场问题的基本公式为麦克斯韦微分方程组，但由于电磁变量相互交织在一起，且都为矢量，求解难度大。通过定义标量电势和矢量磁势把电场和磁场变量进行分离，得到独立的磁场偏微分方程为

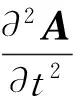
(2)

其中：A为矢量磁势(Wb/m)；J为传导电流密度矢量(A/m2)；μ为磁导率(H/m)；ε为介电常数(F/m)。

电磁作动器电磁力的求解属于有源静态场问题，其电磁场方程可以简化为泊松方程形式。考虑其完全轴对称的结构特点，采用二维轴对称模型进行分析，A和J只有z坐标分量。于是，磁场分布转化为磁势函数的二维边值问题[11]

(3)

其中：Ht为磁场强度的切向分量(A/m)；Γ1为狄里克莱边界条件，即第1类边界条件，应用于除对称轴外的边界；Γ2为诺依曼边界条件，即第2类边界条件，应用于对称轴。

求出Az后，由矢量磁势的定义，电磁感应强度可由下式进行求解

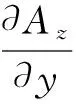
(4)

其中：ex和ey分别为x轴和y轴方向的单位向量。

笔者采用虚功法求解电磁力

(5)

(6)

其中：Wm为积分区域V内的磁场能量；s为虚位移；Fs为物体受到的s方向的电磁力；λ=const表示虚位移发生过程中磁链不变。

2.2 几何建模和网格划分

该电磁作动器中的轴承端盖、线圈架为铝合金材料LY12，其磁导率接近于空气，因此建模时将其当做空气处理，与周围空气连成一片。弹性圆柱销、螺栓和倒角等微小结构以及直线轴承对电磁力的计算影响非常小，建模时予以忽略。衔铁、法兰和壳体材料均为电工纯铁DT4，其导磁性能用B-H曲线定义，其中法兰和壳体采用紧配合，建模时忽略其微小间隙，将法兰和壳体当作一个整体，而法兰、壳体上的齿与衔铁上的齿间留有工作气隙，为0.5 mm。主轴和线圈均为非导磁材料，相对磁导率和空气一样，均设为1。为考虑模型周围的漏磁，将作动器周围一定距离的空气也纳入求解场域中，用长度为200 mm，宽度为50 mm的空气包围作动器模型。采用ANSYS参数化设计语言建立电磁作动器的二维轴对称模型，衔铁与壳体相对位移为零时的模型如图3所示。选择的电磁场分析单元为二维8节点单元PLANE53，设置其单元表现为轴对称。由于几何模型很不规则，直接采用自由网格划分，并控制网格精度等级为3。

图3 几何模型Fig.3 Geometry model

图4 有限元网格划分Fig.4 Finite element mesh generation

2.3 施加载荷和求解

将主轴和衔铁定义为一个单元组件，对其施加力标志，并对线圈施加一定大小的电流载荷。因为主轴材料和空气的磁导率都非常小，故假设求解域以外没有漏磁，即满足磁通量平行条件，将模型对称轴和空气边界上的磁势Az均设置为零。

考虑到求解的非线性，将加载类型设置为斜坡加载，分两个载荷步求解，每个载荷步再设置若干载荷子步，并设置每个载荷子步的迭代次数。求解后，可在通用后处理器中查看电磁场分析结果。

3 试验和仿真结果的对比

图5 试验台实物图Fig.5 Figure of test-bed

如图5所示，将位移传感器、被测作动器、拉压力传感器和电缸依次安装在试验支架上，并保持良好的同轴度。位移传感器的输出为一个电压信号，通过采集卡送入电脑内，利用电压与位移一一对应的关系，通过LabVIEW软件编程求得相应位移。力的测量是利用拉压力传感器中压电晶体的压电效应产生电荷，通过电荷放大器放大后将力实时数字显示。试验时，利用电缸推动被测作动器主轴移动一定位移后停止，调节电源，测出不同电流下作动器输出的电磁力。改变作动器主轴位移，测出对应不同电流下的电磁力。得到不同电流下电磁力与位移的关系，将其与仿真结果进行比较，如图6所示。可以看到，仿真结果与试验数据具有很好的一致性，最大误差仅为11.6%，从而证明了有限元模型的准确性。

图6 不同驱动电流下电磁力仿真值与试验值的对比Fig.6 Comparison of measured and simulation electromagnetic force under different drive current

4 相关参数对电磁力影响规律分析

影响电磁作动器电磁力的参数有齿距、齿宽、齿高、齿数、气隙、衔铁厚度、轭铁厚度、线圈匝数、齿间相对位移和驱动电流等，部分参数如图7所示。

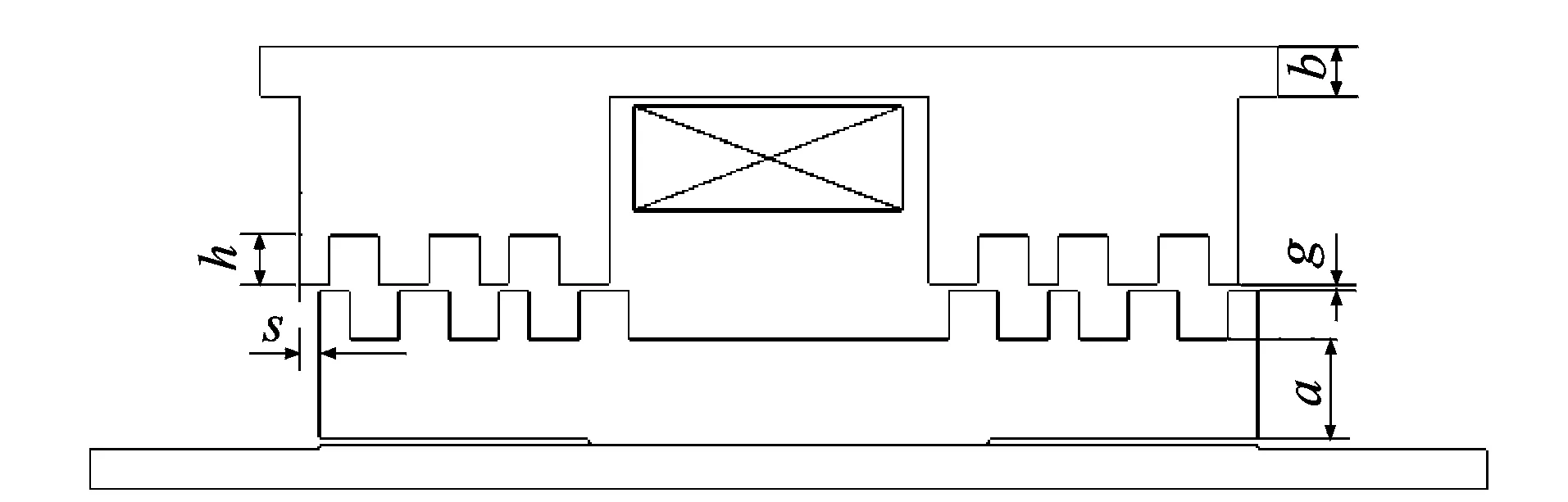
a-衔铁厚度；b-轭铁厚度；h-齿高；g-气隙；s-齿间相对位移图7 电磁作动器结构参数图Fig.7 Structure parameters of electromagnetic actuator

齿距和齿宽对作动器电磁力的大小有一定影响，但主要是影响作动器电磁力-位移特性曲线的形状[12]，在这里不作研究。由于电磁力随齿间相对位移的变化规律比较明确，即在一定范围内基本呈线性关系，故笔者只选取相对位移为2 mm时的情况进行研究。驱动电流不同时，各参数变化对电磁力的影响规律不相同，故研究每个参数对电磁力的影响规律时，都计算其在1，2，4和6 A 4种驱动电流下的变化曲线并进行对比分析。其余6个参数的基准值和取值范围如表1所示，其中，1组齿包括1对大齿和1对小齿。分析某个参数对作动器电磁力的影响时，剩下5个参数取基准值。

表1 参数基准值及变化范围Tab.1 Reference value and variations of parameters

4.1 齿高

图8 不同驱动电流下齿高对电磁力的影响Fig.8 Influence of tooth height on electromagnetic force under different drive current

从图8可以看出，在较大驱动电流下，电磁力随齿高增大呈现先增大后减小的趋势。这是因为增加齿高，一方面会使齿槽散磁减少，导致经过齿部的磁通量增加，进而使工作气隙磁感应强度增大，作动器电磁力增大；另一方面会增大铁磁部分的磁阻，导致磁路中的磁通量有所减少，作动器电磁力降低。可见，齿高改变引起的电磁力变化是这两种因素综合作用的结果。初始时，随着齿高的增加，齿槽散磁的减少导致电磁力增大起主导作用；当齿高增加到一定程度时，齿槽内的散磁小到可以忽略不计，此时经过齿部的磁通量不再增加，电磁力不再增大，导致铁磁部分磁阻增加成为影响电磁力变化的主要因素，使整个磁路磁通量减小，作动器电磁力减小。

在较小驱动电流下，齿高从1 mm增加到7 mm，电磁力随着齿高的增加不断增大，并没有出现减小的趋势，只是增大的程度越来越小。可见，齿高增加导致磁阻增加，进而导致电磁力减小的影响随驱动电流的减小而减少。

4.2 线圈匝数

在不同驱动电流下，电磁力随线圈匝数增加均表现出增大的趋势,如图9所示。这是因为在驱动电流一定的条件下，线圈匝数增加，会使激励匝数增大，从而提高电磁力。需要注意的是，在线圈窗口面积一定的条件下，增加线圈匝数必然导致导线线径的减小，使线圈所能承载的最大安全电流减小。当线圈匝数增大到一定程度时，磁路必将趋于饱和，这将限制电磁力的进一步增大；同时，线圈匝数增多以及导线线径的减小也导致线圈电阻迅速增大，引起热损耗增加。

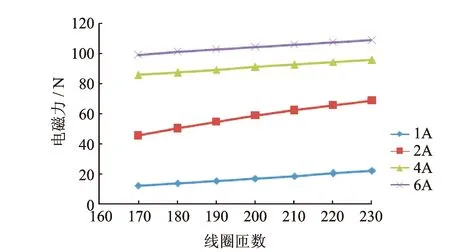
图9 不同驱动电流下线圈匝数对电磁力的影响Fig.9 Influence of coil turns on electromagnetic force under different drive current

4.3 齿数

电磁作动器的电磁力是由多个齿对间的电磁力叠加而成。在各个齿对间的电磁力不变的情况下，若增加齿数，会使总的电磁力成倍增加。然而，增加齿数必然导致经过每个齿对的磁通量减少，各个齿对间的电磁力减小，从而使作动器总的电磁力有减小的趋势。齿数改变对电磁力的影响是这两种因素共同作用的结果。从图10看出，在小驱动电流的情况下，电磁力随齿数的增加而增大；在中等驱动电流的情况下，电磁力随齿数的增加先增大后减小；在大驱动电流的情况下，电磁力随齿数的增加而减小。这说明齿数增多导致经过各齿对的磁通量减小，使电磁力减小的影响随驱动电流的增大而增加。

图10 不同驱动电流下齿数对电磁力的影响Fig.10 Influence of tooth number on electromagnetic force under different drive current

4.4 气隙

由于空气的磁导率远小于电工纯铁DT4的磁导率，故在整个磁路中气隙的磁阻占整个磁路磁阻的绝大部分，减小气隙能够有效减小磁路磁阻、增大磁通量，提高电磁力。从图11中看到，在小驱动电流下，电磁力随气隙的减小而增大。在较大驱动电流的情况下，电磁力随气隙的减小表现出先增大后减小的趋势。这是因为随着气隙的减小，磁路磁阻迅速减小，使磁场在衔铁和轭铁等处产生饱和现象，导致齿间气隙处的磁感应强度的增大受到限制。同时，由于气隙等效导磁面积扩大系数近似与气隙大小成正比[13]，故减小气隙使得齿间气隙的等效导磁面积减小。电磁力与气隙磁感应强度的平方以及等效导磁面积成正比，导致了在较大驱动电流和较小气隙的情况下，电磁力随气隙减小反而变小。

图11 不同驱动电流下气隙对电磁力的影响Fig.11 Influence of air gap on electromagnetic force under different drive current

4.5 衔铁厚度

从图12可以看出，在不同驱动电流下，增加衔铁厚度均能使电磁力增大，且随着驱动电流的增大，电磁力随衔铁厚度增大的幅度越来越大。这是因为增大衔铁厚度会使铁磁部分的磁阻减少，导致整个磁路的磁通量增加，作动器电磁力增大。同时，衔铁厚度的增加会引起衔铁上齿的工作表面直径变大，而衔铁上齿的工作表面直径近似与电磁力成正比[14]，导致电磁力增大。因此，在不同驱动电流下，随着衔铁厚度增加，电磁力都呈现增大的趋势。增加衔铁厚度，还会使磁通沿衔铁轴向的流通面积增加，导致衔铁部分的磁感应强度相对降低，磁场就不会在衔铁部分出现过早饱和，所以驱动电流越大，增大衔铁厚度引起的电磁力增大越明显。

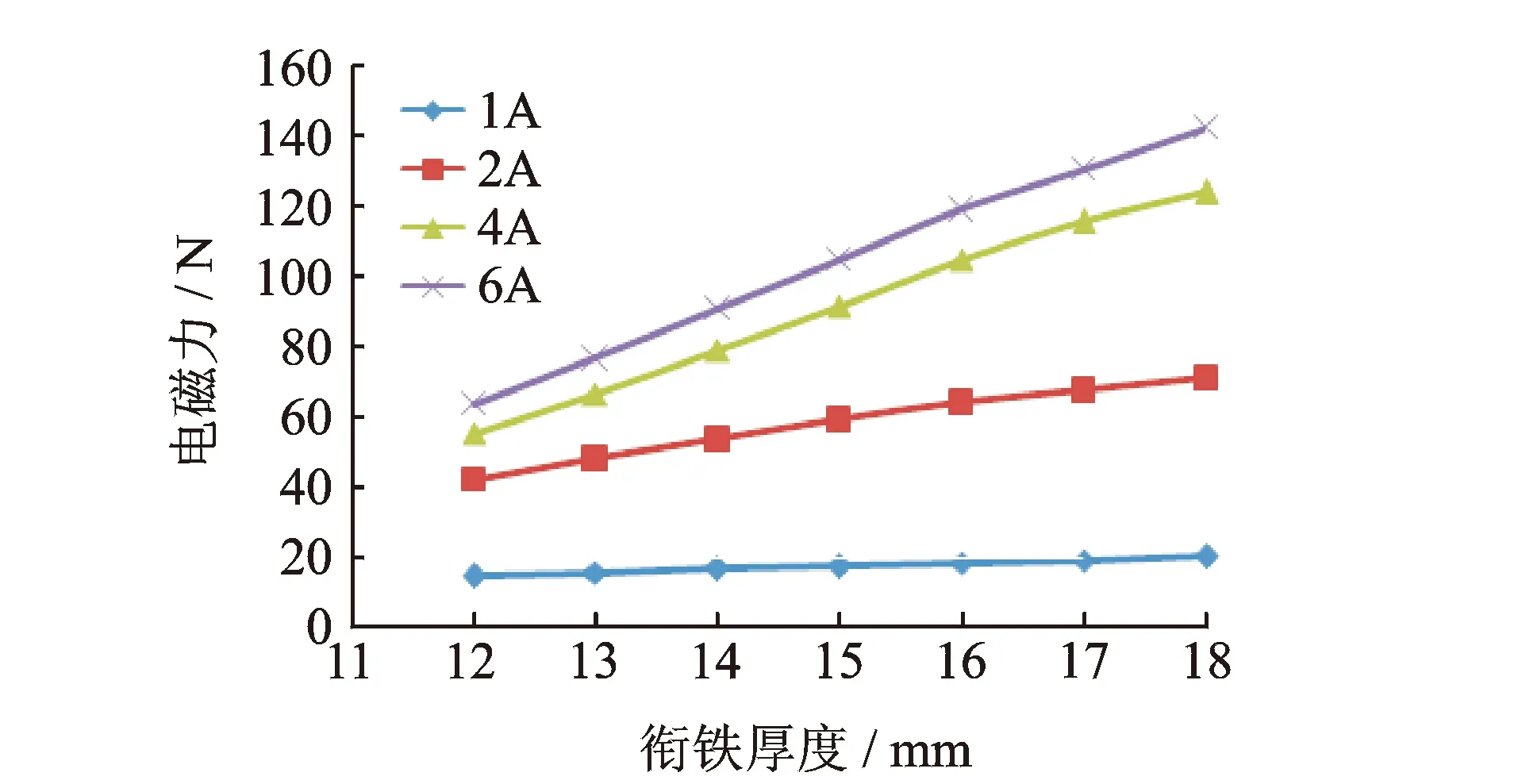
图12 衔铁厚度对电磁力的影响Fig.12 Influence of armature thickness on electromagnetic force under different drive current

4.6 轭铁厚度

图13 轭铁厚度对电磁力的影响Fig.13 Influence of yoke thickness on electromagnetic force under different drive current

从图13看出，当轭铁厚度从2 mm增加到5 mm左右时，电磁力显著增加；当轭铁厚度超过5 mm后，继续增加轭铁厚度，电磁力基本不再增大。这主要是由于增大轭铁厚度可以减小轭铁磁阻，从而使电磁力增大，这种增大作用在一定范围内比较明显，超过一定范围后就几乎不起作用了，反而增大了作动器的尺寸，浪费了材料。同时，在电磁力随轭铁厚度增大而显著增加的区段，随驱动电流增大，电磁力增大的幅度也有所增加。可见，轭铁厚度增加使电磁力增大的影响在大驱动电流时更明显一些。

5 结论

1) 利用ANSYS软件建立了新型电磁作动器仿真计算模型，对加工好的样机电磁力进行了试验测量。结果表明，仿真计算值与试验数据能够很好吻合，最大误差仅为11.6%，证明了所建立仿真模型的准确性，为进一步研究提供了有力工具。

2) 利用试验验证的仿真模型分析了齿高、线圈匝数、齿数、气隙、衔铁厚度和轭铁厚度等参数对电磁力的影响规律：a.在较大驱动电流下，电磁力随齿高增大先增大后减小，在小驱动电流下，电磁力呈现逐渐增大的趋势；b.在不同驱动电流下，电磁力随线圈匝数增多均呈现增大趋势；c.在小驱动电流下，电磁力随齿数增多而增大，在中等驱动电流下，电磁力随齿数增多先增大后减小，在大驱动电流下，电磁力随齿数增多而减小；d.在小驱动电流下，电磁力随气隙减小而增大，在较大驱动电流下，电磁力随气隙减小先增大后减小；e.在不同驱动电流下，电磁力随衔铁厚度增加均呈现增大趋势，且驱动电流越大，电磁力增大越明显；f.在不同驱动电流下，轭铁厚度在一定范围内增大时，电磁力明显增大，超过这一范围后电磁力基本不再增加。

[1] 何琳，徐伟.舰船隔振装置技术及其进展[J].声学学报，2013,38(2)：128-136.

He Lin,Xu Wei.Naval vessel machinery mounting technology and its recent advances[J].Acta Acustica,2013,38(2):128-136.(in Chinese)

[2] Karnopp D，Crosby M J，Harwood R A.Vibration control using semi-active force generators[J].Journal of Engineering for Industry， 1974,96(2):619-626.

[3] Guglielmino E,Edge K A.A controlled friction damper for vehicle applications [J].Control Engineering Practice,2004,12(4):431-443.

[4] Suda Y,Shiiba T,Hio K,et al.Study on electromagnetic damper for automobiles with nonlinear damping force characteristics (road test and theoretical analysis)[J].Vehicle System Dynamics ,2004,41(S):637-646.

[5] Carlson J D,Jolly M R.MR fluid elastomer and foam devices[J].Mechatronics,2000,10(2):555-569.

[6] Jolly M R,Bender J W,Carlson J D.Properties and applications of commercial magnetorheological fluids[J].Journal of Intelligent Material Systems and Structures,1999,10(1):5-13.

[7] 李锐，杜鹏飞，徐文韬，等.基于无量纲分析的磁流变隔振器阻尼参数优化[J].振动、测试与诊断，2014,34(1)：39-45.

Li Rui,Du Pengfei,Xu Wentao,et al.Damping parameter optimization of magneto-rheological isolator via dimensionless analysis [J].Journal of Vibration,Measurement &Diagnosis,2014,34(1):39-45.(in Chinese)

[8] Chen Yong,Zimcik D G，Wickramasinghe V K,et al.Research of an active tunable vibration absorber for helicopter vibration control[J].Chinese Journal of Aeronautics,2003,16(4):203-211.

[9] 周卓亮.可变刚度隔振器研究[D].哈尔滨：哈尔滨工程大学，2006.

[10]石勇，刘友，袁志国.一种柴油机半主动电磁作动器的设计及特性仿真[J].机械设计与研究，2010,26(1)：97-100.

Shi Yong,Liu You,Yuan Zhiguo.A semi-active electromagnetic actuator and its characteristics simulation for vibration isolation of diesel engine[J].Machine Design and Research,2010,26(1):97-100.(in Chinese)

[11]王泽忠.简明电磁场数值计算[M].北京：机械工业出版社，2011:106-122.

[12]项海筹，邵敏.电磁式固有频率可控动力消振器的研究[J].中国机械工程，1992,3(1)：14-16.

Xiang Haichou,Shao Min.Research on electromagnetic natural frequency controllable dynamic vibration absorber[J].China Mechanical Engineering,1992,3(1):14-16.(in Chinese)

[13]官瑞杨，魏新劳，聂洪岩.铁心电抗器气隙等效导磁面积计算[J].哈尔滨理工大学学报，2014,19(4)：6-11.

Guan Ruiyang,Wei Xinlao,Nie Hongyan.The calculation of air gap equivalent cross-sectional area in core reactor[J].Journal of Harbin University of Science and Technology,2014,19(4):6-11.(in Chinese)

[14]Liu Xueguang,Feng Xiaoxiao,Shi Ye,et al.Development of a semi-active electromagnetic vibration absorber and its experimental study[J].Journal of Vibration and Acoustics,2013,135(5)：0510151-0510159.