SiCl自由基X2Π和A2Σ＋态的光谱性质

2015-12-01施德恒孙金锋朱遵略

计算物理 2015年5期

关键词：驱动电流

刘慧，邢伟，施德恒，孙金锋，朱遵略

（1.信阳师范学院物理电子工程学院，信阳 464000；2.河南师范大学物理与电子工程学院，新乡 453007）

杨振1，路兴强1，2，龚学余1

（1.南华大学核科学技术学院，湖南衡阳 421001；2.浙江大学聚变理论与模拟中心，浙江杭州 310027）

文章编号：1001⁃246X（2015）05⁃0610⁃07

SiCl自由基X2Π和A2Σ＋态的光谱性质

刘慧1，邢伟1，施德恒2，孙金锋2，朱遵略2

（1.信阳师范学院物理电子工程学院，信阳 464000；2.河南师范大学物理与电子工程学院，新乡 453007）

采用内收缩多参考组态相互作用（icMRCI）方法结合Dunning等相关一致基，计算SiCl自由基X2Π和A2Σ＋态的势能曲线.讨论参考能和相关能外推对X2Π和A2Σ＋态光谱的影响.对势能进行相对论修正及核价修正计算.拟合势能曲线得到X2Π和A2Σ＋态的光谱常数.它们与实验结果一致.利用Breit⁃Pauli算符，计算旋轨耦合效应，得到X2Π1/2和X2Π3/2的势能曲线、并计算它们的光谱常数.求解双原子分子核运动的径向Schrödinger方程，获得无转动SiCl自由基2个Λ⁃S态及X2Π态的耦合分裂态的全部振动态.得到J＝0时X2Π态的自旋⁃轨道耦合常数、较高振动态的惯性转动常数以及X2Π1/2和X2Π3/2的振动能级等分子常数.

势能曲线；光谱常数；能量外推；自旋－轨道耦合

0 引言

SiCl自由基在半导体工业中具有重要作用.在化学沉积过程中，SiCl自由基是一种重要的反应产物.自1913年Jevons首次观察了SiCl自由基的电子谱［1］以来，已有多人对SiCl自由基开展了实验［2－12］和理论研究［13－14］，获得了若干光谱常数及分子常数.

分析文献［1－14］发现，一方面，对SiCl（X2Π，A2Σ＋）自由基的理论研究有限［13－14］，且计算结果与实验结果偏离较大；另一方面，无论是实验研究还是理论计算，很少报导SiCl的耦合分裂态X2Π1/2和X2Π3/2的光谱.理论预测分子Ω态准确的势能曲线和光谱对实验研究和理论方法的改进有重要意义.

1 理论方法

量化计算中基组达不到完备基组极限是产生误差的一个主要来源.为了提高计算精度，通常采用外推方法减小误差.我们曾经使用总能量外推方法较准确地预测一些分子的势能曲线及光谱性质［15－16］.但这些外推计算未考虑参考能和相关能收敛速度不一致的问题.实际计算中，相关能收敛缓慢.因此参考能和相关能按照相同的收敛指数外推会带来一定的误差.我们用不同的收敛指数将参考能和相关能分别外推来获得势能曲线.

采用内收缩多参考组态相互作用（icMRCI）方法结合Dunning等［17－19］的相关一致基，aug⁃cc⁃pV X Z（X ＝T，Q，5，6），计算SiCl（X2Π，A2Σ＋）的势能曲线.计算是在MOLPRO2010软件包［20］中执行的.

参考能和相关能的总和构成分子的总能量［21－22］

其中，参考能和相关能分别按照下述公式外推至完全基组极限，－α

其中，E∞，ref和E∞，corr是外推至完全基组极限的参考能和相关能．EX，ref和EX，corr是由aug⁃cc⁃pVXZ（X＝T，Q，5，6）基组计算得到的参考能和相关能.指数α和β为经验参数.

这里，使用相邻的aug⁃cc⁃pV X Z和aug⁃cc⁃pV（X－1）Z基组计算得到的参考能EX，ref和EX－1，ref及相关能EX，corr和EX－1，corr，根据（2）式和（3）式导出外推的参考能和相关能分别为

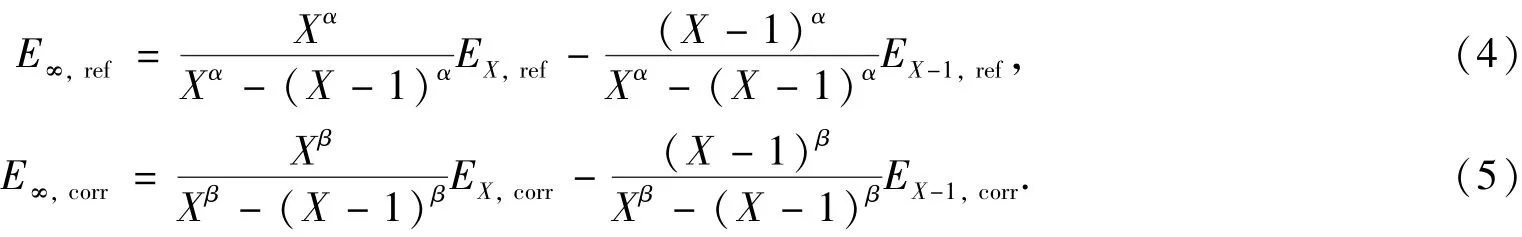
由E∞，ref和E∞，corr可以得到完全基组极限的总能量为

首先采用自旋限制的HF方法得到基态的分子轨道；接着，以HF轨道作为初始轨道，利用完全活性空间自洽场（CASSCF）方法进行轨道优化；再以CASSCF波函数作为参考态，进行icMRCI计算，得到价态范围内SiCl自由基X2Π和A2Σ＋态的势能曲线.

核价相关效应对小分子的能量有较大影响，相对论效应对能量的影响也不容忽略.我们对aug⁃cc⁃pV6Z势能曲线和相邻最大基组aug⁃cc⁃pV5Z和aug⁃cc⁃pV6Z的外推势能进行了核价相关修正和相对论修正.核价相关修正计算使用的基组是aug⁃cc⁃pCV5Z（用CV表示）.相对论修正（用DK表示）计算利用了3阶Douglas⁃Kroll Hamilton近似和cc⁃pV5Z⁃DK相对论收缩基.

利用Breit⁃Pauli算符，计算自旋－轨道效应对SiCl自由基2个Λ⁃S态能量的影响，得到X2Π1/2，X2Π3/2和态的势能曲线、并预测它们的光谱常数.在计算中，Si和Cl原子选择了aug⁃cc⁃pCV5Z基组.

利用SiCl自由基2个Λ⁃S态耦合分裂前后的势能曲线，通过求解核运动的径向Schrödinger方程，获得无转动SiCl自由基的2个Λ⁃S态及X2Π的2个Ω态的全部振动态，计算与每一振动态的振动能级和惯性转动常数等.

2 结果与讨论

2.1 基组外推及各种修正

2.1.1 基组对SiCl（X2Π，A2Σ＋）态平衡位置处的参考能和相关能的影响

将icMRCI/aug⁃cc⁃pV X Z（X＝T，Q，5，6）理论水平下计算的SiCl（X2Π，A2Σ＋）态平衡位置处的参考能和相关能列于表1.

表1中数据显示，随着基组由aug⁃cc⁃pVTZ增大到aug⁃cc⁃pV6Z，X2Π和A2Σ＋态平衡位置处的参考能逐渐降低，相关能逐渐增大，相关能在总能量中的比例逐渐增大.可见，参考能和相关能收敛快慢不同.

2.1.2 基组及外推对SiCl（X2Π，A2Σ＋）态的光谱常数的影响

利用aug⁃cc⁃pV X Z（X＝T，Q，5，6）基组计算了SiCl自由基X2Π及A2Σ＋态的势能曲线.拟合势能曲线得到X2Π态的Re，ωe和De及A2Σ＋态的Re，ωe和Te.这些结果列入表2.将参考能与相关能分别按照（4）式和（5）式外推（选择合适的经验指数α 和β）.根据（6）式得到外推势能曲线.限于篇幅，表2只给出了相邻两个最大基组aug⁃cc⁃pV5Z和aug⁃cc⁃pV6Z的外推结果（表示为56）（其中，α和β分别取3.4和2.4）.为便于比较，我们将最近实验确定的D0［12］和 ωe及 ωexe

［10］结合，利用De＝D0＋ωe/2－ωexe/4导出De，并列入表中.

表1 不同基组下SiCl（X2Π，A2Σ＋）平衡位置处的参考能和相关能Table 1 Reference energy and correlation energy w ith different basis sets

表2 基组、外推及各种修正对SiC l（X2Π和A2Σ＋）的光谱常数的影响Table 2 Spectroscopic parameters w ith different basis sets，extrapolation and core⁃valence correlation and scalar relativistic corrections for SiCl（X2Πand A2Σ＋）

分析表2中数据发现，对于X2Π态，随着基组增大，Re，ωe和De呈现收敛趋势.其中，Re逐渐缩短，ωe和De逐渐增大，且它们向实验结果趋近.但Re，ωe和De与实验结果［5，12］出入较大.在CASSCF/aug⁃cc⁃pV6Z理论水平下，Re，ωe和De与实验结果［5，12］的相对误差分别达到1.20％，3.50％和13.76％.

对于A2Σ＋态，随着基组增大，Re，ωe和Te均收敛.其中，Re逐渐缩短，ωe逐渐减小，Te逐渐增大.它们与实验结果［8］偏离也较大.在CASSCF/aug⁃cc⁃pV6Z理论水平下，Re，ωe和De与实验结果［8］的相对误差分别达到2.55％，8.75％和5.37％.

出现这些结果的原因在于，CASSCF波函数只考虑了多组态因素及活性空间内的相关.而MRCI波函数既考虑了静态相关又考虑了动态相关.基于上述考虑，我们采用icMRCI方法以获得更充分的相关能，并将参考能和相关能分别外推得到X2Π及A2Σ＋态的势能曲线.由此计算了X2Π的Re，ωe和De及A2Σ＋的Re，ωe和Te.它们与实验结果［5，8，12］符合较好.以X2Π态为例，采用参考能和相关能分别外推得到的Re，ωe和De与实验结果［5，8，12］的相对误差分别为0.18％、0.27％及0.55％.而采用总能量外推时的相对误差分别为0.19％，0.33％和0.67％.显然，前者考虑了参考能和相关能收敛速度的不同，因而得到的光谱常数与实验结果［5，8，12］更趋一致.可见，要获得分子准确的能量，在外推计算中必须考虑参考能和相关能收敛快慢不同的问题.上述比较说明，本文进行参考能和相关能外推计算时选择的参数α和β值是适当的，所得到的外推势能曲线可以较准确地描述分子的性质.

2.1.3 核价相关和相对论修正对SiCl（X2Π，A2Σ＋）的光谱常数的影响

由核价相关修正和相对论修正的势能曲线拟合得到SiCl自由基X2Π态的光谱常数Re，ωe和De和A2Σ＋态的Re，ωe和Te.这些常数也列入表2.

由表2可以看出，与aug⁃cc⁃pV6Z的结果相比，对于X2Π态，核价相关修正使Re和De减小、ωe增大；相对论修正使Re增大、ωe和De减小；当同时考虑核价相关修正和相对论修正时，Re和De减小、ωe增大.对于A2Σ＋态，核价相关修正使Re减小、ωe和Te增大；相对论修正使Re和ωe增大、Te减小；当同时考虑核价相关修正和相对论修正时，Re和Te减小、ωe增大.在外推势能曲线加上核价相关修正和相对论修正后，得到的X2Π态和A2Σ＋态结果与实验结果［5，8，12］一致.其中，X2Π态的Re，ωe和De与实验结果［5，12］的相对误差分别仅为0.06％，0.24％和0.08％.A2Σ＋态的Re和Te与实验结果［8］的相对误差分别为0.15％和0.62％.可见，经过各种修正的外推势能曲线可以更准确地描述SiCl自由基的光谱性质.后续的计算都是在这一势能曲线基础上进行的.

2.2 光谱常数

2.2.1 Λ⁃S态光谱常数

利用上述核价相关修正和相对论修正后的外推势能曲线，计算得到SiCl自由基X2Π和A2Σ＋态的光谱常数（Te，De，Re，ωe，ωexe，Be，αe）.这些结果与实验结果［1－9，10，12］及其他理论结果［13－14］一并列入表3中.

表3 SiCl自由基X2Π和A2Σ＋态的光谱常数与实验和其它理论计算结果Table 3 Spectroscopic parameters w ith experimental and theoretical results for SiC l（X2Πand A2Σ＋）radical

文献［13－14］报道了SiCl自由基X2Π态的理论研究.Gosavi等［13］采用HF⁃SCF方法和较小的6⁃31G∗基组计算了该态的Re和ωe.其Re较实验结果［1］偏大2.09％（UHF⁃SCF）和1.99％（RHF⁃SCF）.其ωe偏离最近的实验结果［10］约1.94％.Li等［14］利用CCSD（T）方法和基组外推得到了该态的Re，ωe和De.其Re和ωe与实验结果［1，5］符合较好，相对误差仅为0.24％［5］和0.26％［10］.但是，De与实验值［12］偏离较大，达到3.17％.本文X2Π态的光谱常数Re，ωe，Be和αe与实验结果［3－6，10，12］符合很好.它们与最近的实验结果［10］的相对误差分别为0.06％，0.06％，0.12％和0.49％.各个文献报道的De存在较大差异，本文的De值与实验结果［12］一致（相对误差只有0.08％）.

对于A2Σ＋态，Gosavi等［13］利用HF⁃SCF/6⁃31G∗理论方法计算了该态的Re，它与实验值［8］偏离较大，相对误差分别为7.45％（UHF⁃SCF）和6.80％（RHF⁃SCF）.其采用CISDQ理论方法计算得到的Te与实验结果相差923.8cm－1（4.00％）.本文的Te，Re和Be与实验结果［8］符合较好，它们之间的偏离分别仅为0.62％，0.15％和0.30％.

2.2.2 Ω态光谱常数

自旋－轨道耦合效应对准确预测分子能量意义重大.利用Breit⁃Pauli算符计算自旋－轨道耦合对SiCl自由基2个Λ⁃S态能量产生的影响.在计算中，Si和Cl原子选择了aug⁃cc⁃pCV5Z基组.在自旋－轨道耦合作用下，2Π态分裂为2Π1/2和2Π3/2.而2Σ＋态不发生分裂.根据计算得到的X2Π1/2，X2Π3/2和A2Σ＋1/2的势能曲线，拟合得到它们的光谱常数.其中，A2Σ＋态耦合前后势能曲线的形态未受影响，其光谱常数De，Re，ωe，ωexe，Be，αe的变化微小，可忽略不计.只有该态的激发能Te发生了较为显著改变，升高了101.18cm－1.

将X2Π1/2和X2Π3/2态的光谱常数与实验结果［1］列入表4中以便于比较.

表4 SiCl自由基X2Π1/2和X2Π3/2态的光谱常数与实验结果Table 4 Spectroscopic parameters w ith experimental data for X2Π1/2and X2Π3/2states of SiCl radical

根据计算可知，自旋－轨道耦合导致SiCl自由基X2Π态平衡位置处能量分裂达到202.36cm－1.它与实验结果［1－2，5，9－10］基本吻合.文献［1］报道了X2Π1/2和X2Π3/2的αe值，从表4看，结果与之相符.但是，没有找到其它光谱常数的实验或理论报导.

2.3 分子常数

限于篇幅，表5列出了X2Π态及其2个Ω态的前15个振动态的分子常数G（υ），Bυ和Aυ．为便于比较，将实验结果［6］一同列入表中.文献［7］报导的X2Π态的B0及文献［1］给出的X2Π1/2和X2Π3/2的B0未列入表中.

表5 X2Π态的G（υ），Bυ，Aυ及X2Π1/2和X2Π3/2态的G（υ），Bυ（单位：cm－1）Table 5 Vibrational levels and inertial rotation constantsw ith measurements for X2Π1/2and X2Π3/2states（Unit：cm－1）

从表5可以看出，对于X2Π，本文预测的G（υ）与实验结果［6］一致.例如，υ＝0，3，11时，它们之间的相对误差分别为0.25％，0.29％和0.40％.对于Bυ，本文的B0＝0.255 613cm－1，与实验值0.2552cm－1相符（相对误差仅0.16％）［7］.

文献［1］报道了X2Π1/2和X2Π3/2态的B0，分别为0.2551和0.2556cm－1.本文的B0与其一致，二者之间的偏离分别只有0.17％和0.05％.上述比较表明，本文得到的耦合分裂态的势能曲线是准确的，计算的光谱常数和分子常数是可靠的.可以为今后的相关研究提供参考.

3 结论

采用icMRCI理论方法结合Dunning等相关一致基，aug⁃cc⁃pV n Z（n＝T，Q，5，6），计算了SiCl自由基X2Π和A2Σ＋态的势能曲线.利用参考能和相关能分别外推得到2个Λ⁃S态的外推势能曲线.对势能曲线进行了相对论修正及核价相关效应修正.拟合经过修正的势能曲线得到了SiCl（X2Π，A2Σ＋）的光谱常数.通过自旋－轨道耦合计算，获得X2Π1/2和X2Π3/2的势能曲线，并计算了它们的光谱常数.结果与已有的实验结果符合较好.求解核运动的径向Schrödinger方程，找到了2个Λ⁃S态及X2Π态的2个Ω态的全部振动态.针对每一振动态，计算了与其对应的振动能级、惯性转动常数等分子常数以及X2Π态的自旋轨道耦合常数.它们与已有的实验结果一致.计算了SiCl自由基X2Π态的J＝0时自旋－轨道耦合常数、较高振动态的惯性转动常数及其2个Ω态的振动能级和大部分惯性转动常数.

［1］ Verma R D.A2Δ－2Πtransition of SiCl［J］.Can JPhys，1964，42：2345－2356.

［2］ Oldershaw G A，Robinson K.Ultraviolet absorption spectrum of siliconmono⁃chloride［J］.JMol Spectrosc，1971，38：306 －313.

［3］ Billingsley J.The absorption and emission spectrum of siliconmonoiodide［J］.JMol Spectrosc，1972，43：128－147.

［4］ Rai SB，Singh J，Upadhya K N，et al.Fine structure in the B⁃X system of SiCl［J］.JPhys B：Atom Mol Phys，1974，7：415－419.

［5］ Bredohl H，Demoulin P，Houbrechts Y，et al.Rotational analysis of the B⁃X transition of SiCl［J］.JPhys B：Atom Mol Phys，1981，14：1771－1776.

［6］ Venkataramanaiah M，Lakshman SV J.Potential energy curves and dissociation energy of SiCl［J］.JQuant Spectrosc Radiat Transfer，1981，26：11－13.

［7］ Tanimoto M.Themicrowave spectrum of the SiCl radical［J］.JMol Spectrosc，1984，103：330－336.

［8］ Huber K P，Herzberg G.Molecular spectra and molecular structure IV，constants of diatomicmolecules［M］.Princeton，NJ：Van Nostrand⁃Reinhold，1979：595－596.

［9］ Meijer G，Jansen B，Ter Meulen JJ，etal.High⁃resolution spectroscopy on the B2Σ＋，υ′＝0←X2Π，υ″＝1 transition in SiCl ［J］.Chem Phys Lett，1987，136：519－526.

［10］ Mélen F，Dubois I，Bredohl H.New rotational analysis of the B′2Δ－X2Πrtransition of SiCl［J］.JMol Spectrosc，1990，139：361－368.

［11］ Rajamanickam N，Dhuvaragaikannan N，Mohamed K R.Dissociation energies of LuD and SiClmolecules from experimental potential energy curves［J］.Acta Physica Hungarica，1994，74（4）：385－389.

［12］ Hildenbrand D L，Lau K H，Sanjurjo A.Experimental thermochemistry of the SiCl and SiBr radicals；Enthalpies of formation of species in the Si⁃Cl and Si⁃Br systems［J］.JPhys Chem A，2003，107：5448－5451.

［13］ Gosavi R K，Strausz O P.Molecular orbital studies of the spectral and structural properties of chlorosilylidyne，SiCl［J］. Chem Phys Lett，1986，131：243－246.

［14］ Li H D，Feng H，Sun W G，et al.Diatomic silylynes，germylynes，stannylynes，and plumbylynes：Structures，dipole moments，dissociation energies，and quartet⁃doublet gaps of E H and EX（E＝Si，Ge，Sn，Pb；X＝F，Cl，Br，I）［J］. Inorganic Chemistry，2013，52：6849－6859.

［15］ Liu H，Shi D H，Sun J F，et al.Calculations on thirteenΛ⁃S states of PO radical：Electronic structure，spectroscopy and spin⁃orbit coupling［J］.JQuant Spectrosc Radiat Transfer，2013，121：9－22.

［16］ Liu H，ShiD H，Sun JF，et al.Potential energy curves，spectroscopic constants and spin⁃orbit coupling：A theoretical study on twelve tripletΛ⁃S states of Ge2molecule［J］.Eur Phys JD，2013，67：47－14.

［17］ Dunning TH.Gaussian basis sets for use in correlated molecular calculations.I.The atoms boron through neon and hydrogen ［J］.JChem Phys，1989，90：1007－1023.

［18］ Mourik T V，Dunning T H.Gaussian basis sets for use in correlated molecular calculations.VIII.Standard and augmented sextuple zeta correlation consistent basis sets for aluminum through argon［J］.Int JQuantum Chem，2000，76：205－221.

［19］ De Jong W A，Harrison R J，Dixon D A.Parallel Douglas⁃Kroll energy and gradients in NWChem：Estimating scalar relativistic effects using Douglas⁃Kroll contracted basis sets［J］.JChem Phys，2001，114：48－53.

［20］ Werner H⁃J，Knowles P J，Lindh R，etal.MOLPRO（a package of ab initio programs）［CP/OL］.Version 2010.1.http：∥www.molpro.Net.

［21］ Truhlar D G.Basis⁃set extrapolation［J］.Chem Phys Lett，1998，294：45－48.

［22］ Halkier A，Helgaker T，Jørgensen P，etal.Basis⁃set convergence in correlated calculations on Ne，N2，and H2O［J］.Chem Phys Lett，1998，286：243－252.

文章编号：1001⁃246X（2015）05⁃0617⁃06

外部驱动电流抑制双撕裂模的发展

杨振1，路兴强1，2，龚学余1

（1.南华大学核科学技术学院，湖南衡阳 421001；2.浙江大学聚变理论与模拟中心，浙江杭州 310027）

摘要：在Hall MHD方程组中引入外部驱动电流项，数值模拟外部驱动电流对双撕裂模不稳定性的影响.结果表明，在x点加入反向外部驱动电流对撕裂模的发展有抑制作用，周期性的外部驱动电流对双撕裂模不稳定性的抑制效果较好，能控制磁岛的尺度在相互驱动的临界尺度以下，避免发生双撕裂模非线性磁场重联的爆发，随着驱动电流周期变大抑制效果变坏，在一定限度内随着驱动电流强度增大抑制效果变好，在一定范围内随着驱动电流宽度变小抑制效果变好.

关键词：撕裂模；驱动电流；MHD

0 引言

撕裂模不稳定性大致可分为三大类：即，m≫1，m＞1和m＝1，m表示极向模数．m≫1类型的高模数撕裂模不稳定性，主要引起的是微观不稳定性，研究表明，它增强等离子体的输运［1］，造成等离子体能量损失.对比于m≫1类型来说，m＞1和m＝1类型的破坏性更严重，这两种类型主要是引起等离子体宏观撕裂模不稳定性，甚至可能引起等离子体破裂［2－3］.对于（m，n）＝（1，1）的撕裂模不稳定性，它与等离子体的锯齿波不稳定性相关（n是环向模数）；大量的研究表明（m，n）＝（2，1）撕裂模不稳定性是引起等离子体破裂的主要原因之一，抑制撕裂模不稳定性是目前提高托卡马克装置的约束性能亟待解决的难题.当双撕裂模处在非线性重联阶段时，等离子体动能增长非常迅速，并在有理面上形成剪切流［4］，其破坏性比单撕裂模更严重，所以研究抑制双撕裂模不稳定性的方法具有重大意义.

抑制撕裂模不稳定性的方法有多种，总体来说，是通过直接或间接改变有理面附近的磁剪切来抑制撕裂模不稳定性［5］.目前抑制撕裂模的研究大部分集中在通过局部加热［6－8］或者外部驱动电流［9－10］来改变有理面附近的磁场，从而起到影响撕裂模磁岛发展的作用.

一般而言，抑制撕裂模的方法主要是在磁岛内部加入扰动来抑制撕裂模不稳定性的发展，因而大多数数值模拟都将外部驱动电流的位置选择在磁岛的O点处.外部驱动电流效应是通过欧姆定律方程引入的，合理的外部驱动电流可以减小磁岛的尺度，抑制磁岛增长［11］.本文在Hall MHD方程组的基础上，通过欧姆定律方程引入外部驱动电流效应，模拟外部驱动电流的引入对双撕裂模不稳定性发展的影响，寻求利用外部驱动电流来抑制双撕裂模不稳定性增长的有效方法.

1 物理模型

在大环径比的托卡马克装置中，ε≪1，ε＝a/R，a是托卡马克小圆截面半径，R是大环半径.采用托卡马克平板近似的平衡位形，忽略环效应.标准的磁场可以表示为

为了模型的简化，假设所有变量在环向是常量，在数学上的表述为∂/∂y＝0，将一个空间三维问题简化为二维问题．平板模型中，，，，分别代表托卡马克的极向，环向和径向，ψ是磁通函数.

驱动电流在含Hall效应的欧姆定律［12］中表达式

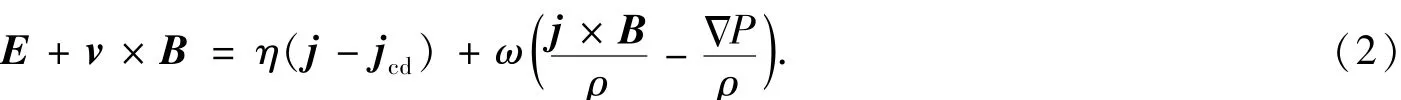
由方程（1），（2）以及连续方程，运动方程，麦克斯韦方程组和状态方程联立，经简化后方程组为

其中，v是等离子体流速，η是等离子体电阻，P是等离子体压强，j是等离子体电流密度（满足自洽场的麦克斯韦方程组），jcd是外部驱动电流（由外部驱动力产生的非感应电流，不满足等离子体自洽场的麦克斯韦方程组）密度，其表达形式

B是磁场，E是电场，其中，欧姆定律中含有Hall项，ω为Hall系数，δ为驱动电流宽度.方程组各个变量由B0，a，TA＝a/vA，ψ0＝aB0等进行归一化.TA，vA分别Alfven时间和Alfven速度.

数值模拟采用二维三分量的MHD模型，径向采用自由边界，极向采用周期边界条件；初始的平衡电流［13］选用分布在两个有理面的哈里斯电流片，初始磁场表示为

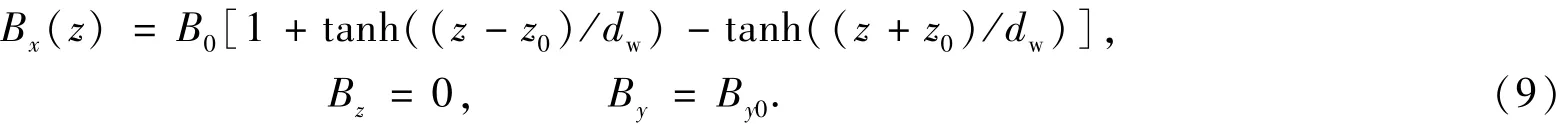
初始的电流和压强满足

本文中z0＝0.5，dw＝0.4，其中，±z0表示有理面的位置，dw表示电流片的宽度，初始等离子体的速度为零.

2 数值模拟结果与分析

2.1 x点反方向驱动电流加载时间对双撕裂模发展的影响

撕裂模不稳定性在两个有理面上发展，开始的增长率以单撕裂模不稳定性增长，随着磁岛逐渐长大，磁岛间相互驱动，进入到双撕裂模发展阶段，在此期间磁场重联非常迅速，磁能将迅速转化为系统的动能，因此系统动能迅速增加，之后由于双撕裂模不稳定性增长非常迅速，严重破坏了托卡马克内磁场位形，撕裂模不稳定性发展也很快进入了衰退期.双撕裂模非线性重联前，在两个磁岛的x点附近加入反向的外部驱动电流，模拟结果如图1所示，x⁃（none）表示没有外部驱动电流时，等离子体动能随时间的演化曲线；x⁃（175），x⁃（200），x⁃（225），分别表示在175，200和225个TA（Alfven时间）时刻加入外部驱动电流，从图中可以看出加入驱动电流的时间越早，更易对等离子体动能的增长起到抑制作用，图1表明，外部驱动电流加入越早，等离子体动能迅速增长的时间相对延后，即对撕裂模的抑制效果更好.

图1 外部驱动电流加入时间对等离子体动能增长的影响Fig.1 Evolution of plasma kinetic energywith different current drive time

2.2 x点附近加入反向周期性电流对双撕裂模发展的影响

在两个磁岛的x点附近加入周期性的反向外部驱动电流，周期为40TA的外部驱动电流变化的形式如图2所示，j0表示外部驱动电流密度幅值，数值模拟结果如图3所示，x⁃（none）代表没有外部驱动电流时等离子体动能变化曲线，x⁃（40），x⁃（60），x⁃（80），x⁃（100），分别代表以40，60，80，100个TA为周期的外部驱动电流，从图3的动能曲线发展情况来看，外部驱动电流的周期越短，动能开始增长越早，而在t＝50TA至275TA时等离子体动能增长相对较慢，但是，在t＞250TA时，较长周期的外部驱动电流对应的等离子体动能增长更缓慢一些.图3表明，周期性的外部驱动电流对双撕裂模不稳定性的抑制效果比较好.

图2 周期性外部驱动电流Fig.2 Periodic current drive

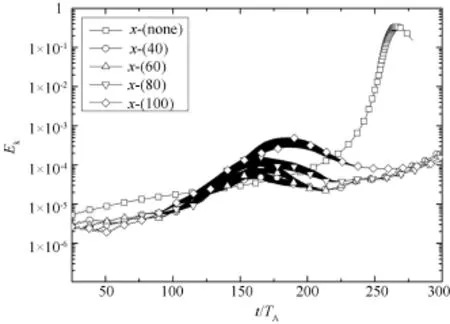
图3 不同周期的外部驱动电流对等离子体动能发展的影响Fig.3 Evolution of plasma kinetic energy with different periodic current drive

为进一步了解周期变化的外部驱动电流对双撕裂模不稳定性的影响，对比加入周期为80TA的外部驱动电流和未加外部驱动电流两种情况的模拟区域环向电流jy剖面演化过程，其中，图4（a），（c），（e），（g）表示无外部驱动电流情况下模拟区域的电流jy剖面随时间的演化过程，图4（b），（d），（f），（h）表示加入周期为80TA的外部驱动电流后模拟区域的电流jy剖面随时间的演化过程.从jy和磁场的演化情况可以很明显的看出加入外部驱电流后磁岛的尺度增长明显变缓.结合图3中等离子体动能变化曲线，表明加入周期变化的外部驱动电流后，等离子体动能曲线并未有出现无外部驱动电流时等离子体动能的非线性增长阶段，即图3，225TA后等离子体动能迅速增长的情况，这表明在加入外部驱动电流后磁岛的发展一直处于两个磁岛单独发展的状态，即磁岛的尺度并未达到双撕裂模非线性磁场重联的临界尺度.

图4 无外部驱动电流时模拟区域环向电流剖面的演化图（a），（c），（e），（g）及加入周期为80 TA的外部驱动电流时模拟区域环向电流剖面的演化图（b），（d），（f），（h）Fig.4 Evolution of current profileswithout current drive（a），（c），（e），（g）and with periodic current drive（80TA）（b），（d），（f），（h）

2.3 周期性的外部驱动电流宽度对双撕裂模发展的影响

为了研究周期性变化的外部驱动电流宽度对双撕裂模不稳定性发展的影响，保持外部驱动电流的强度不变，其周期维持在80TA，仅改变外部驱动电流的宽度.数值模拟结果如图5，其中，x⁃w0.05，x⁃w0.08，x⁃w0.1，x⁃w0.2分别表示驱动电流宽度为归一化长度的0.05倍，0.08倍，0.1倍和0.2倍时，等离子体动能随时间的演化曲线，模拟结果表明在一定范围内外部驱动电流的宽度越窄，外部驱动电流对撕裂模的抑制效果越好，当宽度达到0.2时，外部驱动电流不能使等离子体避免双撕裂模相互驱动，发生快速磁重联.

2.4 周期性的外部驱动电流强度对双撕裂模发展的影响

为了研究周期性变化的外部驱动电流强度对双撕裂模不稳定性发展的影响，保持外部驱动电流的宽度和周期等不变，仅改变外部驱动电流的强度.数值模拟结果如图6所示，其中x⁃80 6.25和x⁃80 3.125分别表示周期为80 TA，电流强度分别占初始电流强度的6.25％和3.125％的外部驱动电流加入后等离子体动能随时间的演化曲线；x⁃（none）表示没有外部驱动电流时等离子体动能随时间的演化曲线.结果表明周期性的外部驱动电流的加入可以抑制双撕裂模的增长，而且一定限度内（不足以驱动产生新的磁岛），外部驱动电流越强抑制效果越明显，当外部驱动电流强度低于一定值时，只能起到延缓作用，不能抑制撕裂模的增长，如，当外部驱动电流强度只占初始电流强度的3.125％时，不能完全抑制双撕裂模的增长.

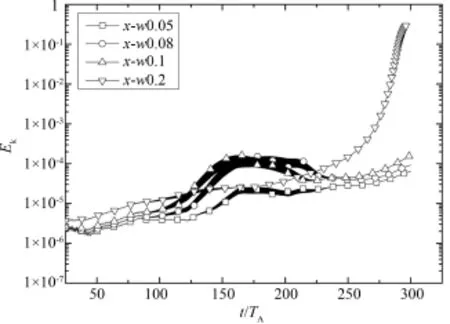
图5 外部驱动电流强度对等离子体动能发展的影响Fig.5 Evolution of plasma kinetic energy with differentwidth of current drive

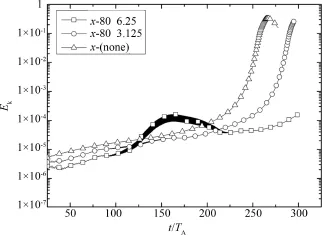
图6 外部驱动电流强度对等离子体动能发展的影响Fig.6 Evolution of plasma kinetic energy with different intensity of current drive

3 结论

对含有外部驱动电流效应的Hall MHD方程组进行数值模拟，研究外部驱动电流对撕裂模不稳定性发展的影响，寻求利用外部驱动电流抑制双撕裂模不稳定性发展的有效方法.模拟结果表明在x点加入与初始电流方向相反的外部驱动电流对撕裂模的发展有抑制作用，进一步的模拟表明周期性变化的外部驱动电流对双撕裂模不稳定性的抑制效果较好，可以控制磁岛的尺度在相互驱动的临界尺度以下，避免双撕裂模非线性磁场重联的爆发；同时还对外部驱动电流的频率，宽度和强度进行了数值模拟，结果表明：在模拟范围内，不同频率的外部驱动电流都能较好地抑制撕裂模不稳定性增长，相比较而言周期为80TA时效果更理想；在模拟范围内，外部驱动电流的宽度越窄，对撕裂模的抑制效果越好；在一定限度内（不足以驱动产生新的磁岛），外部驱动电流的强度越大，对撕裂模的抑制效果越好.通过观察磁岛形成后模拟区域环向电流jy分布的剖面图，如图4（c）所示，可以发现在磁岛形成后，磁岛内部的环向电流jy会被展平、变小，而磁场重联区域的环向电流jy则会逐渐增大.在两个磁岛的x点加入与原电流方向相反的驱动电流，使得x点的环向电流变小，从而影响磁场重联的过程；外部驱动电流越早加入，就能越早的起到减小磁场重联速率的作用；如果加入到x点的驱动电流太小，对磁场的重联速率影响甚微，所以驱动电流要足以影响到磁场重联速率；在总驱动电流大小不变的情况下，加入x点的外部驱动电流宽度越宽，加在重联区域的有效电流越小，抑制效果相对变弱.

参考文献

［1］ Hazeltine R D，Strauss H R.Tokamak heat transport due to tearingmodes［J］.Phys Rev Lett，1976，37：102. ［2］ Wesson J.Tokamaks［M］.Oxford：Oxford University Press，1997，305.

［3］ McGuire K M，Robinson D C.Major disruptions in the TOSCA tokamak［J］.Phys Rev Lett，1980，44，1666.

［4］李新霞，路兴强，龚学余.双撕裂模非线性演化过程中有理面上的剪切流［J］.计算物理，2011，28（6）：831－834.

［5］ Yang Xiaoqing，Wang Shaojie，Yang Weihong.Stabilization of tearingmodes by oscillating the resonant surface［J］.Physics of Plasmas，2012，19：072503.

［6］ Hoshino K，Mori M，Yamamoto T，et al.Avoidance of qa＝3 disruption by electron cyclotron heating in the JFT⁃2M tokamak ［J］.Phys Rev Lett，1992，69：2208.

［7］ Classen IG J，Westerhof E，Domier CW，et al.Effect of heating on the suppression of tearingmodes in tokamaks［J］.Phys Rev Lett，2007，98：035001.

［8］ Petty C C，La Haye R J，Luce T C，et al.Complete suppression of the m＝2/n＝1 neoclassical tearingmode using electron cyclotron current drive in DIII⁃D［J］.Nucl Fusion，2004，44：243.

［9］ Westerhof E，Lazaros A，Farshi E，et al.Tearingmode stabilization by electron cyclotron resonance heating demonstrated in the TEXTOR tokamak and the implication for ITER［J］.Nucl Fusion，2007，47：85.

［10］ Liu Y，Gong X，Yang L，et al.Numerical solution of fullwave equation for fastwave current drive in Tokamak［J］.Chinese J Comput Phys，2012，29（3）：375－382.

［11］ Hegna CC，Callen JD.Interaction of bootstrap⁃current⁃drivenmagnetic islands［J］.Phys Fluids B，1992，4：1855.

［12］ Zhang C L，Ma ZW，Dong JQ.A simulation study of hall effect on double tearingmodes［J］.Plasma Sci Technol，10：407. ［13］ Chen L，LeiW，Wu B.Numerical study on effectof equilibrium current profile on resisitivewassmode stability［J］.Chinese J Comput Phys，2013，30（6）：902－908.

Abstract： Effects of external current drive on instability of double tearingmode in Hall MHD equations are numerically investigated. It shows that double tearingmode can be suppressed by antiparallel external current drive at x⁃point of tearingmodemagnetic islands. Periodic external current drive controls island width under a threshold and stabilizes double tearing mode.With increasing period depression effect becomes worse.If frequency，density and width of periodic external current drive are adopted suitably，depression effect becomes better.

Key words： current drive；tearingmode；MHD

Spectroscopic Properties of SiCl（X2Π，A2Σ＋）Radical

LIU Hui1，XINGWei1，SHIDeheng2，SUN Jinfeng2，ZHU Zunlue2（1.College of Physics＆Electronic Engineering，Xinyang Normal University，Xinyang 464000，China；2.College of Physics＆Electronic Engineering，Henan Normal University，Xinxiang 453007，China）

Potential energy curves（PEC）of ground X2Πand A2Σ＋states of SiCl radical are calculated with internally contracted multireference configuration interaction approach in combination with Dunning’s correlation⁃consistentbasis sets.Reference energy and correlation energy are extrapolated to complete basis set limit.Scalar relativistic and core⁃valence correlation corrections are calculated. Spectroscopic parameters of X2Πand A2Σ＋states are obtained.With Breit⁃Pauli operator，PECs of X2Π1/2and X2Π3/2states are computed.Spectroscopic parameters of twoΩstates are determined.Vibrationmanifolds are evaluated for twoΛ⁃Sand twoΩstates of non⁃rotation SiCl radical by numerically solving radical Schrödinger equation of nuclearmotion.For each vibrational state，vibrational levels and inertial rotation constants，spin⁃orbital coupling constants of X2Πstate are determined.

potential energy curve；spectroscopic parameter；extrapolation of energy；spin⁃orbital coupling

Stabilization of Double Tearing M ode by External Current Drive

YANG Zhen，LU Xingqiang，GONG Xueyu （School ofNuclear Science and Technology，University of South China，Hengyang，Hunan 421001，China）

O561.3

.2 文献标志码：A

2014－08－29；

2014－12－08

国家自然科学基金（61077073），河南省科技计划项目（142300410201）及河南省教育厅科技计划重点项目（14B140023）资助项目

刘慧（1969－），女，硕士，副教授，主要从事原子与分子光谱研究，E⁃mail：liuhuixytc＠126.com

Received date： 2014－08－29；Revised date： 2014－12－08

收稿日期：2014－10－20；修回日期：2015－02－05

基金项目：国家热核聚变实验堆（ITER）计划专项（2014GB108002），国家自然科学基金（41104094，11375085）、教育部博士点基金（20114324120002）和南华大学核聚变与等离子体物理创新团队课题（NHCXTD03）资助项目