基于MKurt-MOMEDA的齿轮箱复合故障特征提取*

2017-09-12王志坚王俊元赵志芳吴文轩张纪平寇彦飞

振动、测试与诊断 2017年4期

关键词：峭度齿轮箱特征提取

王志坚，王俊元，赵志芳，吴文轩，张纪平，寇彦飞

(中北大学机械与动力工程学院太原， 030051)

基于MKurt-MOMEDA的齿轮箱复合故障特征提取*

王志坚，王俊元，赵志芳，吴文轩，张纪平，寇彦飞

(中北大学机械与动力工程学院太原， 030051)

针对齿轮箱中旋转零部件的故障信号是周期性的冲击信号这一特性，提出了一种基于多点峭度(multipoint kurtosis,简称MKurt)和多点最优最小熵反褶积(multipoint optimal minimum entropy deconvolution adjusted，简称MOMEDA)的齿轮箱复合故障特征提取方法。利用MKurt可以有效提取齿轮箱中被噪声淹没的冲击性振动信号的周期，实现对振动信号振动源的追踪。根据故障的周期设置合理的周期区间，通过MOMEDA对原信号进行降噪，进一步提取原信号的周期性冲击。通过仿真信号和实测数据的分析和验证，证明了MKurt-MOMEDA方法可以准确有效地诊断齿轮箱复合故障故障特征。

多点峭度；最优最小熵反褶积；复合故障；特征提取

引言

齿轮箱是复杂机械系统使用最广泛的机械，其中齿轮、轴承等零部件也最易损坏。当齿轮箱中轴由于不对中、齿轮和轴承的内外圈或滚动体发生故障时，传动系统将会受到影响，振动信号会出现周期性脉冲信号[1-3]。当齿轮箱出现多种故障时，传感器测取的信号为各种源信号的叠加信号，这些源信号在传递过程中往往发生不同程度的畸变或混叠，在复合故障中表现的尤为明显。因此，复合故障特征之间互相耦合、相互干扰，尤其在强背景噪声下，微弱故障常被噪声淹没，难以提取特征信息。可见，多故障特征的提取仍然是一个大的挑战[4-6]。

峭度作为无纲量参数，其值与轴承或齿轮的转速、尺寸和载荷均无关，但对冲击信号特别敏感，适用于表面损伤、早期裂纹的故障诊断[7]，可通过峭度反映信号的奇异程度，但其不能提供更多的关于故障位置等信息。文献[8]提出了基于峭度图的信号处理方法，并成功应用于轴承和齿轮的故障诊断中。文献[9]将最小熵反褶积(minimum entropy deconvolution,简称MED)用于滚动轴承与齿轮故障诊断，此方法的基本原理是利用最大峭度值作为迭代终止条件[10]，通过解卷积最优的滤波器，使信号突出少数大的尖脉冲。王志坚等[11-12]通过MED和总体经验模态分解(ensemble empirical mode decomposition,简称EEMD)二次降噪的方法提取轴承的微弱故障特征，但MED降噪只能突出少数大的尖脉冲，对复合故障的微弱成分的特征提取无能为力。为了弥补MED的局限性，McDonald等[13]提出最大相关峭度反褶积(maximum correlated kurtosis deconvolution，简称MCKD)算法。此方法引入相关峭度的概念，以相关峭度最大化作为目标函数，通过迭代算法优化最佳滤波器，成功地运用在齿轮的故障诊断中。利用MCKD方法可以有效提取故障信号中被噪声淹没的周期冲击成分,抑制信号中的噪声,实现信号降噪,提升原信号的峭度[14]。MCKD受两个参数的限制，分别为滤波器的长度和故障周期，使其不具有自适应性。通过大量仿真信号分析发现，滤波器长度增大将增加计算量，故障周期必须取整，若为非整数，需要对其重采样并取整。由于MCKD只能提取出有限个冲击成分，因此该方法在很大程度上受到约束。McDonald等[15]提出了MOMEDA的齿轮箱故障诊断方法，此方法适用于周期性故障特征提取，它使用一个时间目标向量定义解反褶积确定所得的脉冲位置。该算法不需要迭代即可获取最佳滤波器，也不需先验确定故障的周期。笔者通过多点峭度谱图确定故障周期的大小，设置合理的故障区间，通过MOMEDA提取故障特征。该方法有效识别封闭式功率流试验台的复合故障特征。

1 多点优化最小熵反褶积

Cabrelli[16]对脉冲反褶积提出了一种新的准则，称为D范数，并用几何学证明了反褶积问题。D范数反褶积问题可以通过一个准确的非迭代求解方法对滤波器系数进行求解。文献[15]提出一种基于多重D范数(multi D-norm，简称MDN)的多脉冲目标识别的反褶积算法主要应用于周期性脉冲的故障特征提取，并引入了MOMEDA。

假设采集到的响应信号为

(1)

其中：e(n)为噪声；x(n)为冲击序列；h(n)为传递函数；y(n)为采集到的振动信号。

MOMEDA算法本质就是寻找一个FIR滤波器，通过输出信号x(n)尽可能恢复输入信号y(n)。

MOMEDA是一种针对位置已知的多脉冲目标识别反褶积算法，能够识别连续的冲击脉冲。引入的最大值问题的解即为MOMEDA。

(2)

(3)

其中:t为确定脉冲位置和权重的常数矢量。

利用归一化水平表示达到的最佳目标解，可提取不同采样率的故障周期，也可以识别同一采样频率下不同故障特征的周期。因此，通过目标矢量t可实现脉冲信号的分离和位置的确定。

通过对滤波器系数(f=f1,f2,…,fL)求导数，得到式(3)的极值为

(4)

(5)

进一步简化为

t1M1+t2M2+…+tN-LMN-L=X0t

通过导数等于0解出极值，式(5)变为

(6)

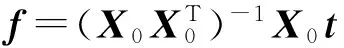
MOMEDA滤波器和输出解可概括为

(7)

(8)

(9)

目标矢量t和输出结果具有相同的长度(N-L+1)，目标矢量表示在输出中解反卷积脉冲的位置和权重，控制了脉冲的位置，且MOMEDA方法通过非迭代取得最优解，为旋转机械周期性故障诊断提供了基础。OMEDA可对M个连续的目标矢量进行如下计算，此时式(7)，(9)变成式(10)，(11)。

(10)

(11)

通过MOMEDA降噪，求解反褶积的位置是唯一的，对单一故障而言，不需要考虑周期是否为整数或滤波器的长度对降噪的影响。在整个采样区间内，每个周期都会出现一个周期性冲击脉冲。多级传动的齿轮箱内部特征频率分布较宽，故障周期为多个时，对复合故障的追踪效果不佳。为了准确提取复合故障特征，引入了多点峭度作为特征提取的度量标准。

(12)

当输出结果y与目标矢量t相同时，MKurt归一化得到

(13)

得到标准化因子

(14)

最终，标准化的多点峭度被定义为

(15)

此定义是基于峭度提出的，但其目标矢量在受控位置处被扩展为多个脉冲，进一步被归一化。实际上旋转机械每转动一周，可能存在两个或多个故障冲击成分，多点峭度达到峰值时可能对应的故障周期并非只有一个。当多点峭度达到峰值时，对应的采样点数(周期)即为故障周期，也可能为周期的整数倍或半倍等。因此，多点峭度可以对故障周期和周围的非故障进行区分，其中多点峭度和采样点数均为无量纲量。

为了提取复合故障特征，首先，计算原信号的多点峭度，确定复合故障的周期；其次，设置合理的故障周期区间，假设某复合故障存在两个故障周期，分别为40和120，如果设置一个故障周期区间为[10～200]，通过MOMEDA降噪时只能提取较强的冲击成分，另一故障将被误认为噪声造成误诊断现象，此时可设置两个周期区间，分别为[10～80]和[100～150],每个周期区间含有唯一的故障周期；最后，分别对原信号进行MOMEDA降噪，即可分别获取这两个周期区间的冲击脉冲。

仿真信号如图1所示。复合信号e由噪声信号a、正弦信号b和冲击信号1组成。其中，冲击性周期为90，信号e可知冲击信号1已被噪声淹没。为了确定冲击性信号1的周期，对其求解多点峭度，结果如图2所示。在周期为30，45，90，180和270处均出现峰值，分别对应于冲击性信号1周期的半倍、1/3和整数倍关系。如图3所示，为了进一步提取冲击脉冲信号1，对组合信号e进行MOMEDA降噪,成功提取周期为90的冲击信号。

文献[15]和上述仿真信号分别对单一故障特征提取，为了验证此方法提取多故障特征的能力，对含有两个冲击成分如图1的仿真信号f进行分析，它包含了两个冲击成分，周期分别为90和140。图4对应其多点峭度谱图，显然在谱峰处周期为30，45，90，180，270，360分别对应冲击信号1的1/3倍、0.5倍和整数倍；70，140，280分别对应冲击信号2的0.5倍和整数倍。多点峭度可以确定多故障对应的周期，为了进一步提取故障信号，需要设定恰当的周期范围。因为两个冲击周期分别为90和140，因此分别设定周期为[50～100]，[100,150]，设定步长ΔT=0.1，经过MOMEDA降噪成功提取出冲击信号1和2，如图5，6所示。

图1 仿真信号Fig.1 Simulation signal

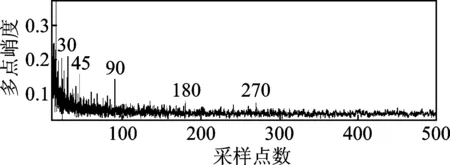
图2 仿真信号e的多点峭度谱图Fig.2 Multipoint kurtosis spectrum of simulation signal e

图3 仿真信号e的MOMEDA降噪Fig.3 MOMEDA noise reduction of Simulation signal e

图4 仿真信号f的多点峭度谱图Fig.4 Multipoint kurtosis spectrum of simulation signal f

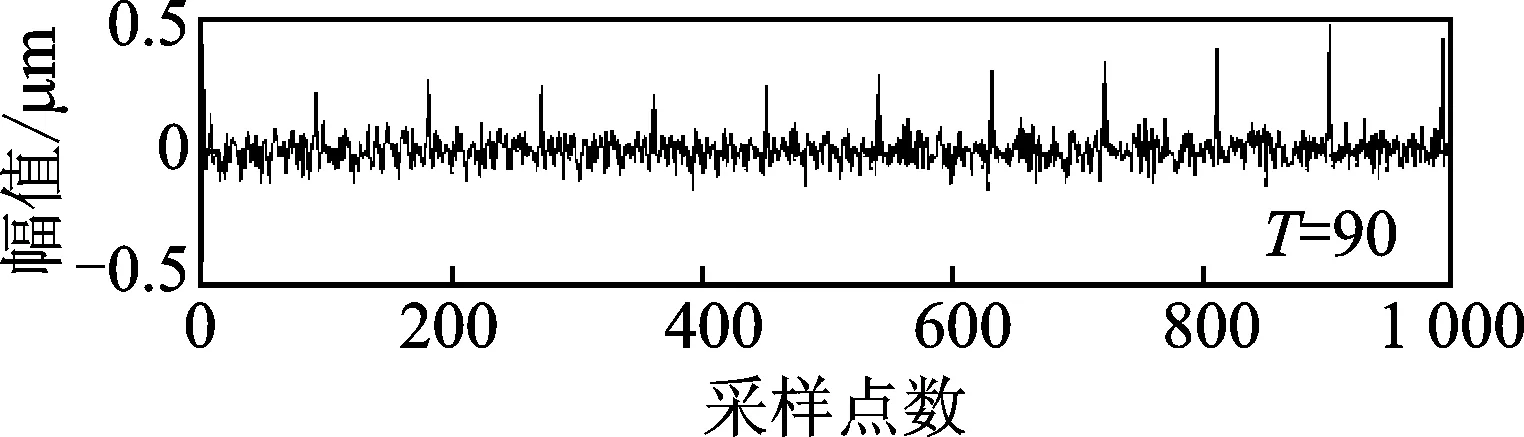
图5 仿真信号f的MOMEDA降噪提取冲击信号1Fig.5 MOMEDA noise reduction of Simulation signal f to extract the impact signal 1

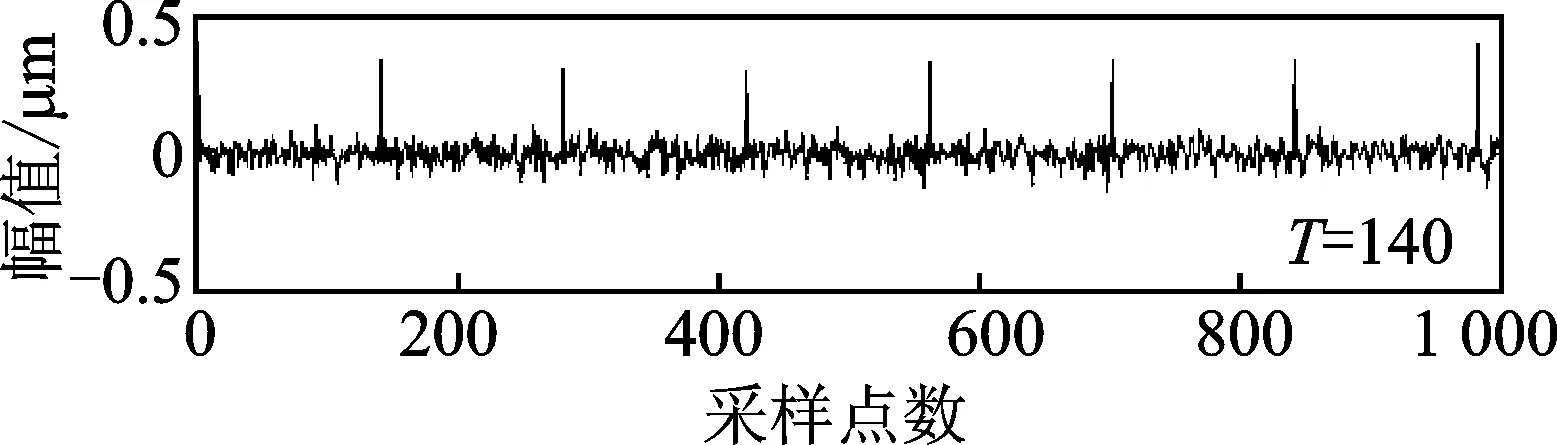
图6 仿真信号f的MOMEDA降噪提取冲击信号2Fig.6 MOMEDA noise reduction of Simulation signal f to extract the impact signal 2

2 齿轮箱多故障特征识别

试验装置如图7所示，试验齿轮为18个，试验轴承型号为32212，试验齿轮的传动比为1∶1，采取半齿啮合，转速为1 200r/min，采样频率为8kHz，正常和故障的齿轮和轴承试验负载均加载到1kNm，采集信号的传感器型号为YD77SA三向加速度传感器(灵敏度为0.01V/ms2)，采样数为2 048个，轴的转动周期为400，轴承滚珠故障周期为111.1，齿轮的啮合频率为360Hz，齿轮的啮合周期为22.4。齿轮箱故障类型为两个：第1个为齿轮点蚀故障，如图8所示；第2个为轴对不中，齿轮轴每转动一周可产生一个周期性冲击[12]。

图7 齿轮传动试验台Fig.7 Rig for gear transmission testing

图8 轴承齿轮故障示意图Fig.8 Gear fault diagram

图9 健康齿轮时域波形Fig.9 Time-domain waveform of healthy gear

图10 点蚀齿轮时域波形Fig.10 Time-domain waveform of pitting gear

图11 健康齿轮箱多点峭度谱图Fig.11 Multipoint kurtosis spectrum of healthy gear box

图12 故障齿轮箱多点峭度谱图Fig.12 Multipoint kurtosis spectrum of faulty gear box

图13 故障齿轮箱MOMEDA降噪Fig.13 MOMEDA noise reduction of faulty gear box

同一个加速度传感器同一个方向测得齿轮箱健康和故障的振动信号时域波形如图9，10所示。正常齿轮振动波形比较平滑且幅值较小，当齿轮箱出现故障时，会出现明显冲击振动，幅值有所增加，基本上是正常齿轮幅值的4倍左右，且有明显周期成分出现，周期为400，对应轴的转动周期，另一冲击成分在时域波形中并不能确定。为了确定故障位置，分别对健康和故障下的振动数据进行多点峭度谱图分析，如图11，12所示。显然，周期为22.4，44.8，67.2和134.4代表齿轮的啮合周期及其倍数的关系，100.8，201.6和403.2代表轴的转动周期及其因子。通过对比可知，齿轮故障多点峭度的峰值明显强于健康齿轮箱的峰值，峰值保持在两倍左右，说明齿轮有缺陷。如图13所示，为了进一步提取冲击成分，设置周期区间为[10～50]和[350～450]，通过MOMEDA降噪，成功提取齿轮的点蚀故障和轴的不对中故障。

3 结论

1) MOMEDA克服了MED和MCKD的缺点，可以将每个周期的故障冲击提取出来，但只能对单一故障特征提取。

2) MKurt能够求解复合故障冲击性周期，在周期的倍数或半倍处均有谱峰出现。在噪声环境中此方法具有免疫性，为了进一步提取冲击性脉冲，可通过设置降噪周期的区间来控制解卷积的脉冲位置。

3) 该方法为复合故障特征提取提供了一种新思路，具有一定的工程应用价值。

[1] Georgoulas G,Loutas T,Stylios C D,et al.Bearing fault detection based on hybrid ensemble detector and empirical mode decomposition[J].Mechanical Systems &Signal Processing,2013,41(1-2):510-525.

[2] Randall R B,Antoni J.Rolling element bearing diagnostics-a tutorial[J].Mechanical Systems &Signal Processing,2011,25(2):485-520.

[3] Lei Yaguo,He Zhengjia,Zi Yangyang.EEMD method and WNN for fault diagnosis of locomotive roller bearings[J].Expert Systems with Applications an International Journal,2011,38(6):7334-7341.

[4] Bachschmid N,Pennacchi P,Vania A.Identification of multiple faults in rotor systems[J].Journal of Sound &Vibration,2002,254(2):327-366.

[5] Patel T H,Darpe A K.Coupled bending-torsional vibration analysis of rotor with rub and crack[J].Journal of Sound &Vibration,2009,326(3):740-752.

[6] Wang Yanxue,Liang Ming.Identification of multiple transient faults based on the adaptive spectral kurtosis method[J].Journal of Sound &Vibration,2012,331(2):470-486.

[7] 张超,陈建军.基于LMD和Lempel-Ziv指标的滚动轴承故障损伤程度研究[J].振动与冲击,2012(16):77-82.

Zhang Chao,Chen Jianjun.Fault severity assessment for rolling element bearings based on LMD and Lempel-Ziv index[J].Journal of Vibration and Shock,2012(16):77-82.(in Chinese)

[8] 彭畅,柏林,刘小峰.基于鲁棒性小波包峭度图的滚动轴承故障诊断[J].振动、测试与诊断,2016(1):11-16.

Peng Chang,Bo Lin,Liu Xiaofeng.Robust wallet transform-based kurtogram for the fault diagnostics of rolling element bearing[J].Journal of Vibration,Measurement &Diagnosis,2016(1):11-16.(in Chinese)

[9] Sawalhi N,Randall R B,Endo H.The enhancement of fault detection and diagnosis in rolling element bearings using minimum entropy deconvolution combined with spectral kurtosis[J].Mechanical Systems &Signal Processing,2007,21(6):2616-2633.

[10]张丹,隋文涛.MED方法及在滚动轴承故障诊断中的应用[J].机床与液压,2014(23):185-187.

Zhang Dan,Sui Wentao.MED method and application in fault diagnosis of rolling element bearings[J].Machine Tool &Hydraulics,2014(23):185-187.(in Chinese)

[11]王志坚,韩振南,刘邱祖,等.基于MED-EEMD的滚动轴承微弱故障特征提取[J].农业工程学报,2014,30(23):70-78.

Wang Zhijian,Han Zhennan,Liu Qiuzu,et al.Weak fault feature extraction of rolling bearing based on MED-EEMD[J].Transactions of the Chinese Society of Agricultural Engineering,2014,30 (23):70-78.(in Chinese)

[12]Wang Zhijian,Han Zhennan.A novel procedure for diagnosing multiple faults in rotating machinery[J].ISA Transactions,2015 (55):208-218.

[13]McDonald G L,Zhao Qing,Zuo Ming.Maximum correlated kurtosis deconvolution and application on gear tooth chip fault detection[J].Mechanical Systems and Signal Processing,2012,33:237-255.

[14]武兵,贾峰,熊晓燕.基于最大相关峭度反褶积的轴承故障诊断方法[J].振动、测试与诊断,2014(3):570-575.

Wu Bing,Jia Feng,Xiong Xiaoyan.Bearing fault diagnosis based on maximum correlated kurtosis deconvolution[J].Journal of Vibration,Measurement &Diagnosis,2014(3):570-575.(in Chinese)

[15]Mcdonald G L,Zhao Qing.Multipoint optimal minimum entropy deconvolution and convolution fix:application to vibration fault detection[J].Mechanical Systems &Signal Processing,2016,82:461-477.

[16]Cabrelli C A.Minimum entropy deconvolution and simplicity:a noniterative algorithm[J].Geophysics,1985,50(3):394-413.