单点激光连续扫描测振的薄壁圆筒件模态测试*

伍济钢，袁继广，蒋 勉，张双健

(湖南科技大学机械设备健康维护湖南省重点实验室 湘潭，411201)

单点激光连续扫描测振的薄壁圆筒件模态测试*

伍济钢，袁继广，蒋 勉，张双健

(湖南科技大学机械设备健康维护湖南省重点实验室 湘潭，411201)

针对薄壁圆筒构件模态测试的需求，提出了基于单点激光连续扫描测振的薄壁圆筒构件模态测试方法。根据纯模态分析理论，在研究两端固定细弦自由振动的基础上，理论上建立了单点激光测振仪在两端固定的自由振动细弦上做连续扫描所得的振动信号和弦的模态振型之间的关系，研究了并提出了激光测振仪输出信号的处理方法。搭建了单点激光连续扫描测振的薄壁圆筒构件模态测试平台，对薄壁圆筒构件进行了模态实测，获得了薄壁圆筒构件前五阶固有频率和相应的模态振型，并对测试结果进行了有限元模态分析验证。结果表明，模态振型一致,固有频率误差在5%以内，证明了提出方法的正确性和有效性。

单点激光连续扫描； 振动测量； 薄壁圆筒构件； 模态测试

引 言

薄壁圆筒构件具有重量轻、材料用量少和结构紧凑等优点，广泛应用于工业生产各个领域。薄壁圆筒构件刚度较低，在设备运行过程中易产生过度振动形成振动噪声甚至引起故障，因此必须对薄壁圆筒构件进行模态测试。

国内外学者对薄壁构件的振动及模态测量问题进行了大量研究。传统的采用振动传感器加力锤锤击的模态宽频测试方法会因粘贴传感器引入附加质量而改变薄壁构件的模态，同时存在测点少、空间分辨率低等问题[1-2]。激光测振技术以其非接触式测量、测量精度高等特点在振动测量中得到了广泛的应用，解决了传感器对薄壁构件产生附加质量的问题，同时也没有安装空间的限制。Stanbridge等[3]运用多普勒激光测振仪测得了平板的工作振型。Maio等[4]以旋转的碟式刀片为研究对象，研究了多普勒激光测振仪在旋转对称结构工作振型测量上面的应用。卢喜丰等[5]以中空的薄壁长方体模型和白车车身为研究对象，采用单点激光测振仪对其进行试验模态分析，得到在固支条件下模型各个面的固有频率及振型，克服了单头激光测振系统难于测试三维空间结构模态的局限性。李旺益等[6]通过对飞机模型纯模态试验，提出了一种把纯模态试验理论和激光测振相结合的激光纯模态测试方法。文献[7-9]设计了试验平台，将圆筒固定在带有旋转台的振动台上，通过旋转台的旋转带动圆筒结构的转动，结合激光测振技术，实现了对圆筒结构的工作振型测量，但在测量过程中会引入一些不相干的振动，从而影响振动测试结果。可见，采用先进的激光测振技术进行薄壁圆筒构件的模态测试是工业生产的必然需求[10]。

针对薄壁圆筒模态测试的需求，笔者提出了单点激光连续扫描测振的薄壁圆筒模态的模态测试方法，对薄壁圆筒构件进行高效、高精度和全视野振动测量，实现了薄壁圆筒构件的快速、高精度、高分辨率模态测试。

1 单点激光连续扫描测振的薄壁圆筒构件模态测试原理

1.1 测试方案

如图1所示，模态测试系统由4部分组成，分别为薄壁圆筒构件及其悬挂支撑、棱镜直线和旋转扫描运动及其控制系统、激光测振仪及其支撑、激振系统。薄壁圆筒构件用4根柔性绳悬挂实现自由支撑，4根柔性绳的固有频率相对于薄壁圆筒构件的第1阶固有频率要小得多，对测试结果影响非常小。棱镜直线运动为一套导轨导槽结构，工作时导槽固定，导轨由伺服电机驱动进行移动；棱镜旋转运动通过伺服电机旋转轴上用夹具固定了一45°直角棱镜实现，以改变激光在薄壁圆筒里的方向，使激光直射到薄壁圆筒的内壁，伺服电机旋转实现内壁的圆周扫描。激振系统中的振动控制器会产生正弦信号，经功率放大器放大加载到激振器上，带动薄壁圆筒构件产生同频振动。同时，激振器的振动信号经加速度传感器反馈到振动控制器，保证激振器产生激振信号的精度。当伺服电机旋转时，相应测点的振动由激光测振仪转化为对应的电压信号。DAQ采集卡同步采集这一电压信号，经计算机分析处理得到扫描运动轨迹上的模态振型。

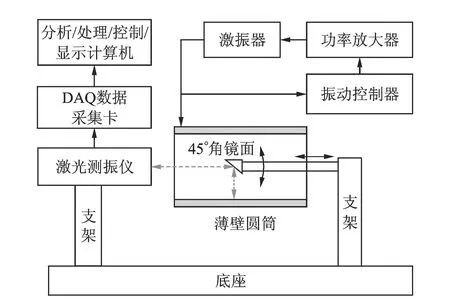
图1 单点激光连续扫描测振的薄壁圆筒构件模态测试方案Fig.1 Modal testing scheme for thin-sheet cylinder parts based on single-point laser continuous scanning vibrometry

1.2 扫描振动信号与模态振型的关系

激光测振仪扫描的轨迹为薄壁圆筒构件的圆周，根据其起始点可展开成一直线，用激光在两端固定的自由振动弦上连续扫描的输出振动信号来研究与其模态振型之间的关系。如图2所示，假设有一根细弦张紧于两固定点之间，弦的单位长度的质量为ρ(x)，在横向分布力f(x,t)作用下作横向振动，张力为T(x,t)，跨长为L，弦x处的横向位移函数为y=y(x,t)。

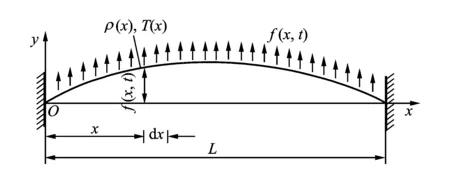
图2 两端固定的振动弦Fig.2 Vibrating string with both ends fixed

如图3所示，取微段弦线单元体dx并假设弦作微小横向振动，由牛顿定律可得

(1)

图3 微段振动弦线Fig.3 Micro section of vibrating string

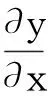
(2)

假设弦的单位长度质量ρ(x)=ρ，并为常数，横向位移y(x,t)为小量，弦内张力T可以视为常量，则式(2)简化为

(3)

如果f(x,t)=0，则弦的自由振动微分方程为

(4)

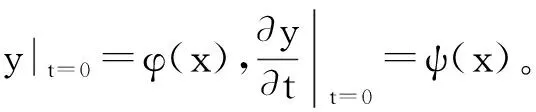
用分离变量法进行求解，得到

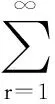
(5)

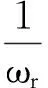
弦的振动为一系列振幅、频率和相位不同的驻波的叠加，即y(x,t)为弦在某一边界条件下的振动状态，而这一振动是由模态叠加所得。当激光在振动弦上以恒定速度v做连续扫描测振时，激光的位置和时间的关系可以用x=vt表示，将其代入式(5)，得到激光在弦上做连续扫描测振时输出振动位移的时域信号为

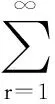
(6)

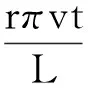
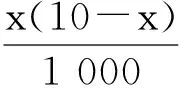
(7)

将x=vt代入式(7)，得到激光测振仪输出的振动位移时域图，如图4所示。当r分别等于1,2,3时，弦的前三阶模态振型和相应的激光测振仪输出的振动位移时域图中的上下交替包络线完全等同于在这一阶固有频率下的模态振型。这为研究激光连续扫描测量振动体的模态振型提供了理论基础。

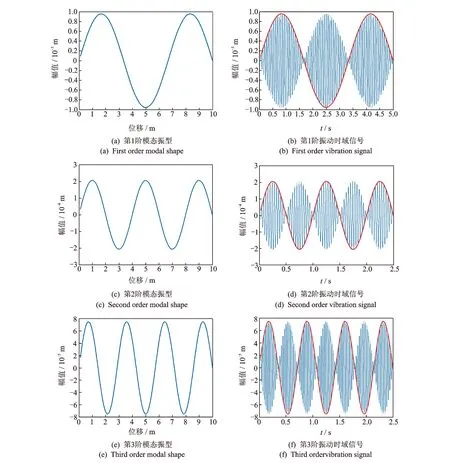
图4 振动弦前三阶模态振型及其相应的振动时域图Fig.4 Vibration mode of vibrating string in former three orders and its vibration time domain figures

1.3 激光测振仪的输出信号处理方法

为了得到测试对象在固有频率振动下相应的模态振型，必须对DAQ采集卡采集的激光测振仪的输出信号进行相应的信号处理。

图5为信号处理流程图。由DAQ采集卡输出的信号为电压信号，经灵敏度校核处理后转变为速度信号。在测量过程中信号不可避免地会加入很多噪声，因此必须对信号进行滤波。由于多普勒激光测振仪测得的电压信号对应的为振动速度，测试需要的是振动位移信号，因此必须将速度信号转化成位移信号。经位移信号幅值点的滑动平均，得到位移信号的上下交替包络线；但这些点构成的包络线可能会因为测量误差等因素影响其光滑度，所以还必须进行曲线拟合光滑处理，最后得到固有频率下的模态振型。

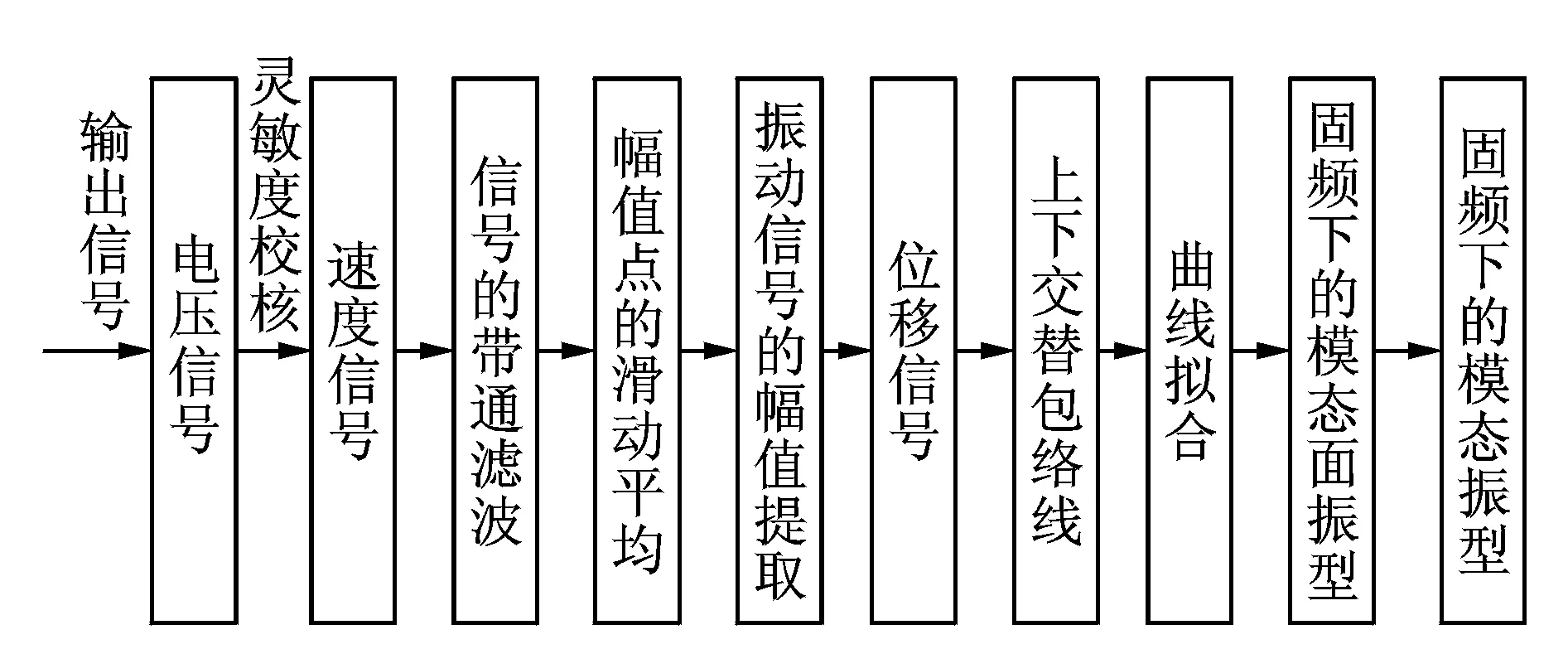
图5 激光测振仪输出信号处理工作流程Fig.5 Processing flow chart for outcoming signal of laser vibrometry

振动信号的包络线其实是振动信号每个周期的幅值点组成的曲线，分为上包络线和下包络线。在测试对象由稳定正弦激励信号激振产生的受迫振动中，上下包络线关于x轴对称。要求取上下交替包络线，先找到上包络线靠近x轴的极小值和下包络线靠近x轴的极大值作为判断条件。构造一个新的向量，按条件依次将幅值点赋给此向量，得到向量包含的上下交替包络线。具体流程如图6所示。

图6 上下交替包络线求取的程序流程Fig.6 Calculation flow chart for upper and lower alternate envelope

直角棱镜的匀速旋转最终使激光束在薄壁圆筒内表面以恒定的线速度运动，直接获得的是整个薄壁圆筒构件内壁的模态振型，还必须将其转化为真实的薄壁圆筒构件的模态振型。直角棱镜的角速度θ与激光束的线速度v的关系为

v=rθ

(8)

其中：r为圆筒的内半径。

二维平面振型变为三维立体振型的公式为

(9)

其中：(xk，yk)为变化后的坐标；Δy为平面振型中每个点所对应的幅值；θ0为激光束在薄壁圆筒构件内壁扫描对应的初始角；Δθ为直角棱镜旋转的角度增加量；k为对应的采集点序号。

1.4 激振位置选择

为了保证系统的可辨识性，一般要求激励点不应该靠近节点或者节线太近。这就要求最佳激励点的位移响应值不等于零。最佳激励点定义为

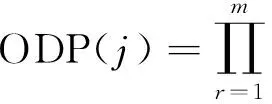
‖φjr‖

(10)

其中：r为模态阶数。

(11)

定义第j个自由度的平均驱动自由度加速度为

(12)

激励点的选择应避免选在最佳激励点的值为零的点。如果在这些点激振，激振力再大，模态也是很难被激出来。另外，应该选择自由加速度较大的位置，因为在这些点会导致激振器的附加质量对被测物体影响较大。考虑到各方面因素，激励点选择在靠近圆筒一端边缘上的某个点上[11]。

2 单点激光连续扫描测振的薄壁圆筒构件模态实测

2.1 测试平台的搭建

根据单点激光连续扫描测振的薄壁圆筒构件模态测试原理搭建测试平台，如图7所示。

图7 薄壁圆筒构件的模态测试平台Fig.7 Modal testing platform for thin-sheet cylinder parts

2.2 测试结果及分析

图8为薄壁圆筒构件模态测试扫频试验时的激振系统驱动电压。可以看出，在10～350 Hz之间，薄壁圆筒构件共有5阶固有频率，分别为39.9，123.0，153.9，169.3和293.6 Hz。分别在相应固有频率下对薄壁圆筒构件进行定频分析，给激振器施加相应的正弦激励，可激出各自的模态振型。通过单点激光连续扫描测振，获得相应的振动信号；对振动信号进行处理，获得每一阶频率下的振型。

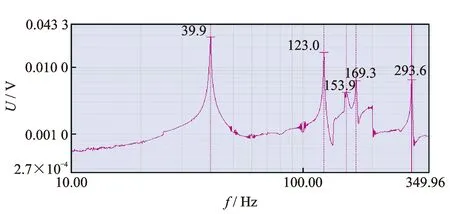
图8 扫频试验中激振系统的驱动电压Fig.8 Driving voltage of exciting system in in sweep frequency experiments

3 与薄壁圆筒构件有限元模态分析的对比

薄壁圆筒构件的内直径为284 mm，厚度为2 mm，高度为80 mm，材料为结构钢，密度为7 850 kg/m3，弹性模量为2×1011Pa，泊松比为0.3。利用ANSYS软件，在Workbench中对薄壁圆筒构件进行模态分析。图9为薄壁圆筒构件的有限元模型。

图9 薄壁圆筒构件的有限元模型Fig.9 Finite element model of thin-sheet cylinder parts

表1为有限元模态分析与模态实测的固有频率对比。薄壁圆筒构件有限元模态分析的前5阶固有频率分别为38.2，117.4，149.9，164.9和280.1 Hz，与模态实测得到的固有频率基本相同，误差保持在5%以内。

表1 有限元模态分析与模态实测的固有频率对比Tab.1 Results comparison of natural frequency between finite element analysis and experimental test

图10为薄壁圆筒构件有限元模态分析和模态实测的前五阶振型对比。可以看出：第1阶模态振型的截面都类似为一椭圆；两者的第2阶振型也类似为一椭圆，同时表现为在“椭圆”的长径处向外翻转，短径处向内翻转；第3阶振型都呈现为类似三菱柱的形状；两者的第4阶振型除了表现类似三菱柱的形状外，同时“三菱柱”的边也都有存在翻转；第5阶振型两者都呈现四棱柱的形状。可见，单点激光连续扫描测振得到的模态振型和有限元模态分析得到的模态振型基本一致，仅存在一些细微的差别，这主要是由于试验中一些复杂因素在仿真中无法模拟[12]而造成的。

图10 有限元模态分析和模态实测的前5阶振型对比Fig.10 Former five order vibration mode comparison between finite element analysis and experimental test

4 结束语

针对薄壁圆筒构件模态测试的需求，突破了激光连续扫描测振方法在视角上的制约，提出了薄壁圆筒构件模态振型的快速、高精度测试方法。根据纯模态分析理论，在研究两端固定细弦自由振动的基础上，理论上建立了单点激光测振仪在两端固定的自由振动细弦上做连续扫描所得的振动位移信号和弦的模态振型之间的关系，得出扫描所得的振动时域信号的上下交替包络线即为扫描路径的模态振型的结论。研究了振动信号的处理方法，提出了上下交替包络线的求取方法。搭建薄壁圆筒构件模态测试平台，对薄壁圆筒构件进行模态测试，获得薄壁圆筒构件前五阶固有频率和相应的模态振型，并对测试结果进行有限元模态分析验证。固有频率误差在5%以内、模态振型一致，证明了提出方法的正确性和有效性。

[1] 段海洋.薄壁圆柱壳振动特性的研究[D].沈阳:东北大学,2012.

[2] 刘彦琦,褚福磊.几何参数对旋转薄壁圆柱壳振动特性的影响[J].振动与冲击,2012(1):22-25.

Liu Yanqi,Chu Fulei.Effects of geometric parameters on vibration characteristics of rotating thin circular cylindrical shell[J].Journal of Vibration and Shock,2012(1):22-25.(in Chinese)

[3] Stanbridge A B,Martarelli M，Ewins D J.Measuring area vibration mode shapes with a continuous-scan LDV[C]∥Proceedings of the Fourth International Conference on Vibration Measurements by Laser Techniques.Ancona,Italy:International Society for Optics and Photonics，2000,4072:176-183.

[4] Maio D D,Ewins D J.Applications of continuous tracking SLDV measurement methods to axially symmetric rotating structures using different excitation methods[J].Mechanical Systems and Signal Processing,2010,24:3013-3036.

[5] 卢喜丰.实验模态分析与激光测振技术研究[D].成都:西南交通大学,2007.

[6] 李旺益.纯模态激光测试法的研究[D].南京:南京航空航天大学,2008.

[7] Daborn P M，Ind P R，Ewins D J.Enhanced ground-based vibration testing for aerodynamic environments[J].Mechanical Systems and Signal Processing,2014(49):165-180.

[8] Giuliani P，Maio D D，Schwingshackl C W,et al.Six degrees of freedom measurement with continuous scanning laser doppler vibrometer[J].Mechanical Systems and Signal Processing,2013(38):367-383.

[9] Zucca S,Maio D D,Ewins D J.Measuring the performance of underp latform dampers for turbine blades by rotating laser Doppler vibrometer[J].Mechanical Systems and Signal Processing,2012(32):269-281.

[10]肖良瑜,李建伟,宋大凤,等.立式屏蔽电机半速涡动异常振动试验分析[J].振动、测试与诊断,2015,35(2):316-321.

Xiao Liangyu,Li Jianwei,Song Dafeng,et al.Analysis of abnormal vibration of half speed eddy for vertical canned motor[J].Journal of Vibration,Measurement &Diagnosis,2015,35(2):316-321.(in Chinese)

[11]贺良国,刘永斌,张连生,等.基于压电激振的弹性模量测量方法[J].振动、测试与诊断,2014,34(6):1080-1083.

He Liangguo,Liu Yongbin,Zhang Liansheng,et al.Research on measuring method of elastic modulus by piezoelectric excitation resonance[J].Journal of Vibration,Measurement &Diagnosis,2014,34(6):1080-1083.(in Chinese)

[12]田永卫,闫楚良,张书明,等.飞机随机振动环境实测试验数据的归纳方法[J].振动、测试与诊断,2014,34(6):1129-1133.

Tian Yongwei,Yan Chuliang,Zhang Shuming,et al.Inductive method of flight test data measured from aircraft random vibration environment[J].Journal of Vibration,Measurement &Diagnosis,2014,34(6):1129-1133.(in Chinese)

10.16450/j.cnki.issn.1004-6801.2017.04.007

* 国家自然科学基金资助项目(51205122)

2015-06-10；

2015-08-24

TH113.1

伍济钢，男，1978年8月生，博士、副教授。主要研究方向为机械动力学和机器视觉测量等。曾发表《Rotor crack fault diagnosis based on base and multi-sensor adaptive weighted information fusion》(《Journal of Software》2012,Vol.7,No.7)等论文。 E-mail：jgwu@foxmail.com