固定式三向铣削测力仪的研究*

赵玉龙，李莹雪，,费继友，秦亚飞，李秀源

(1.西安交通大学机械制造系统工程国家重点实验室 西安，710049)(2.大连交通大学动车运用与维护工程学院 大连，116028)

◀专家论坛▶

固定式三向铣削测力仪的研究*

赵玉龙1，李莹雪1，2,费继友2，秦亚飞1，李秀源1

(1.西安交通大学机械制造系统工程国家重点实验室 西安，710049)(2.大连交通大学动车运用与维护工程学院 大连，116028)

由于铣刀在铣削过程中切削位置不同，固定型铣削测力仪将产生输出误差。为降低铣削位置变化对传感器输出的影响，研制了一种四竖直敏感梁结构的应变型固定式三维铣削测力仪。研究表明,当铣削位置范围限定时，该测力仪可以将输出信号误差维持在可用范围，并分别进行了静态力测量和动态铣削实验。在静态力测量实验中，在70 mm×70 mm×15 mm工件上，传感器解耦偏差不大于5.58%；在动态切削实验中，使用相同加工参数在不同位置处铣削，传感器测得的铣削力峰峰值最大相差3.73%。对该铣削测力仪的研究为解决竖直方向高刚度的应变型固定式铣削力传感器的解耦问题提供了新的思路和参考。

固定式三向铣削测力仪；应变式传感器；竖直弹性梁；偏心受力；偏心受力解耦

引 言

铣削力是判断刀具状态、预测加工质量、改进刀具设计参数和优化加工工艺等重要依据[1-4]，对铣削力的测量一直是智能装备领域的核心研究课题之一。应变型固定式铣削测力仪因其相对低廉的成本和易于维护的简单结构成为铣削力测量的重要手段之一[5]。固定式铣削力传感器使用时安装在铣台上，工件固定在传感器顶板上。固定式测力仪上的受力点会随铣刀的加工位置不断变化，当铣削力的作用点不与传感器顶板中心重合时，测力仪的敏感梁可能会发生附加变形，传感器的输出信号与中心受力时相比可能发生变化，这为求解传感器统一的解耦矩阵带来了问题。

由三向测力仪的解耦矩阵可知，当受力点变化时，测量电路中主测量分量的输出变化和交叉耦合分量的变化是影响传感器解耦精度的两个主要因素。黄震等[6]在对高频响铣削测力仪的解耦研究中发现，如不引入与受力点位置相关的力矩标定矩阵，在10 mm×4 mm×4 mm工件上，传感器的三向测量误差分别达到8% ～ 9%,20% ～ 35%和60% ～ 90%。文献[7]发现在装夹16方外圆车刀时，由于车刀刀尖相对于刀柄中心的偏移量的不同(最大偏移约为12 mm)，使垂直式八角环结构三维车削测力仪的对称梁间的交叉耦合输出分量最大相差3.18%。许林云等[8]在对平行式八角环三向测力传感器的研究中，通过改变贴片位置，降低力Fz在以Fx为主测量分量测量电路中的输出，使受力点沿x和y方向移动时，交叉耦合不大于7.76%。袁哲俊等[9]设计的四直筋式铣削测力仪利用应变片串联补偿方法，将受力点移动引起的主测量分量和交叉耦合分量的变化进行了抵消。笔者[10]也利用相似的方法对十字梁结构铣削力传感器进行了解耦测量，使静态力解耦偏差不大于4.87%。以上对固定式测力仪的解耦研究，目前仅有水平直梁结构的测力仪设计来降低受力点的三维位置移动的影响，但该传感器竖直方向刚度较低，对提高动态性能不利。笔者对竖直方向刚度较大的测力仪、降低受力点位移效应的解耦方法作为研究重点进行测力仪设计。

笔者提出的竖直梁固定式三向铣削测力仪不需额外的受力点位置识别补偿算法，仅凭解耦矩阵可在35 mm×35 mm×15 mm的偏移范围内，将主测量分量的输出误差限制在不大于4.98%、交叉耦合分量的输出误差限制在不大于3.69%的范围内。这既符合机床测力传感器的静态标定要求(力加载点位置偏移时，主测量分量输出变化不大于5%，交叉耦合分量输出变化不大于10%)[11]，又为研制具有高刚度的并联式敏感梁结构铣削力传感器打下基础。

1 传感器偏心力解耦原理分析

设计的三向竖直梁固定式铣削测力仪的弹性体结构和测量电路如图1所示。测量电路全部使用惠斯通半桥电路，R为应变片初始阻值；R0为定值电阻值；测量电路X,Y和Z的主测量分量分别为Fx,Fy和Fz。采用敏感梁局部坐标系进行应变分析，以各梁的纵向轴线为x轴，以该轴线与底座的交点作为原点。xL为局部坐标系中的坐标变量，应变片1 ～ 16分别沿轴向粘贴在xL= 0或xL=l处，应变片17 ～ 32两两垂直，分别粘贴在xL=l/2附近。

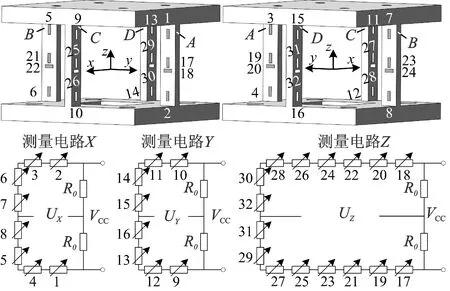
图1 固定式铣削力传感器示意图Fig.1 Diagrams of fixed milling force sensor

将固定式铣削测力仪的载物平台和工件视作刚体，当敏感梁质量相对较小时，根据力的平移定理，施加的偏心外力可以等效为通过该刚体底面中心点的外力与一个附加力偶之和，此力偶矩等于该原始偏心外力对该中心之矩。以该中心受力时传感器的输出信号为基准，当传感器在大小和方向相同的非中心外力作用下，欲保持输出信号不变，比较前后两者输入的区别，测力仪在附加力偶单独作用下的输出信号需尽量减少，理想状态下为零。如表1所示，将该附加力偶分解到直角坐标系上，分别对传感器在单一力偶矩分量作用下的输出信号进行讨论。

表1 附加力偶的矢量分解Tab.1 Vector decomposition of additional moments

1.1 Mxy或Myx作用下的传感器输出

当Mxy或Myx施加在刚体底面中心所在xy平面时，敏感梁变形如图2(a)所示。传感器单个敏感梁上的表面轴向应变为

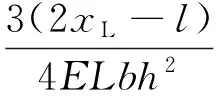
(1)

其中：b，h和l分别为敏感梁的宽度、厚度和长度；L为传感器中心台面边长的一半；E为材料的弹性模量；i为敏感梁A～D的编号；Mxy可替换为Myx。

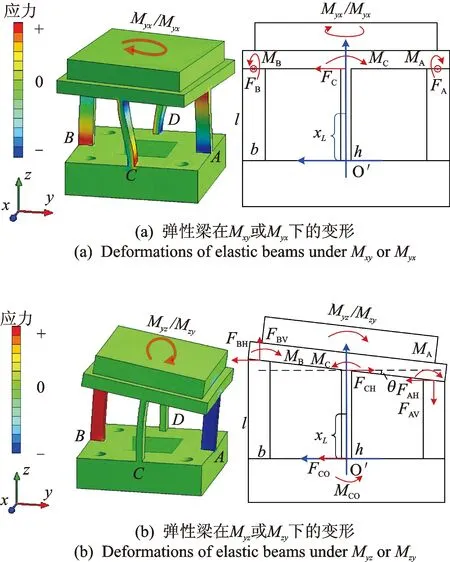
图2 弹性梁在偏心力作用下的变形Fig.2 Deformations of elastic beams under eccentric forces

将xL带入式(1)，传感器测量电路的输出为

UX(Mxy)=UY(Mxy)=UZ(Mxy)=0

(2)

其中：U为测量电路的输出电压。

可见，Mxy和Myx对传感器输出端的影响可以通过惠斯通电桥电路消除。当Mxy和Myx作用于传感器时，对测量电路的输出基本没有影响。

1.2 Myz或Mzy作用下的传感器输出

当Myz或Mzy施加在刚体底面中心yz平面时，敏感梁的变形如图2(b)所示。各敏感梁侧壁轴线上的轴向应变为

(3)

其中：Mzy可替换为Myz。

将xL的值带入式(3)，传感器测量电路输出电压为

(4)

由式(4)可知，Mzy或Myz对测量电路X和Z基本无影响，但对测量电路Y的影响无法完全通过惠斯通电桥电路消除。

y向附加力偶分量作用的情况与x向力偶作用近似，通过以上分析，将传感器非中心受力与中心受力时输出相比较，非中心受力对测力仪的输出影响如表2所示。其中:Y代表有影响;N代表无影响。

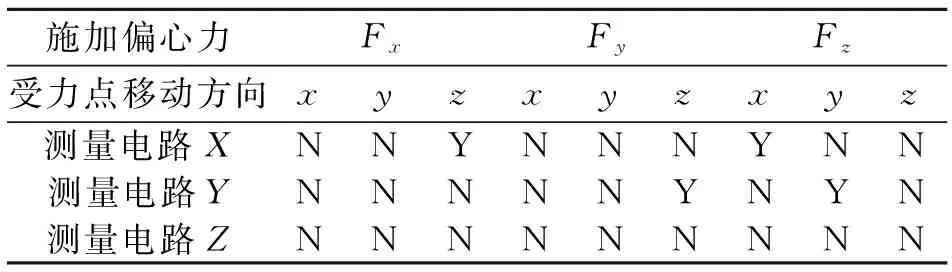
表2 非上板底面中心点受力对传感器输出的影响Tab.2 The influence of eccentric force on sensor output

1.3 敏感梁尺寸优化对传感器输出的影响

除了表2列出的27种偏心力作用的情况下，仍有4种情况下传感器的输出信号受到受力点位置移动的影响，但这部分误差可以通过尺寸优化降低。以传感器上板中心受力的输出电压为基准，受力点沿x或y方向移动时，测量电路X或Y在Fz的作用下的输出误差EX(Fz)或EY(Fz)用式(5)表示

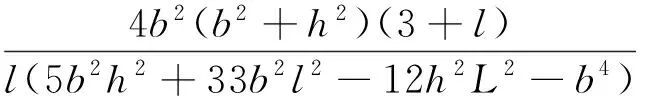
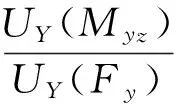
(5)

其中：UY(Fy)为Fy作用于刚体底面中心时测量电路Y的输出；Ly为力的作用点到该中心的y向距离；EY，Ly和UY(Fy)可以被EX，Lx和UX(Fx)代替。

当受力点沿z方向移动时，测量电路X或Y的输出误差EX(Fx)或EY(Fy)可表示为

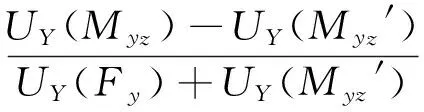
(6)

其中：Lz为力的作用点到传感器上板底面中心点的z向距离；载物台z向厚度记为Lz’；EX(Fx)和EY(Fy)的表达式相同。

由式(5)和式(6)可知，以上输出误差都与Q成正比，传感器的尺寸优化使用其中一项作为目标函数即可，此处选用EX(Fz)。由于需要满足5b≤l和5h≤l，考虑到对贴片操作空间的要求，取l=50 mm，则b≤10 mm，h≤10 mm，取L=50 mm，传感器上板厚度为10 mm，此时Ly=35 mm。在保持弹性梁横截面面积基本不变的前提下，选取5对(b，h)计算EX(Fz)，如图3所示。使用ANSYS软件对敏感区应变进行仿真，利用应变量与输出电压的线性关系计算EX(Fz)。当施力点位于Lx=Ly= 50 mm时，仿真结果如图3所示。

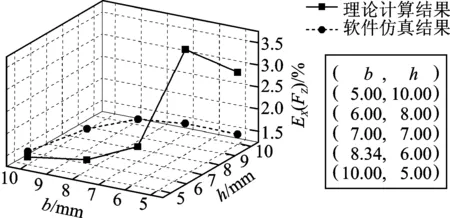
图3 Fz在测量电路X中引起的信号输出误差Fig.3 The output errors of measuring circuit X under Fz

如图3所示，当b=10 mm，h=5 mm时，EX(Fz)较小(理论计算结果为1.43%，仿真结果为1.55%)，且受传感器上板厚度等其他因素的影响最小。因此，选用该尺寸制作传感器敏感梁，会将4种无法完全消除的力作用点的偏心影响降到最低。

2 传感器静态受力实验

2.1 传感器的制作

如图4所示，传感器上板尺寸为100mm×100mm×10mm，竖直梁尺寸为5mm×10mm×50 mm，材质为17-4PH不锈钢，选用蚌埠天光传感器公司生产的1 kΩ单栅半导体应变片贴装，并在应变片表面敷以硅胶进行保护。

图4 四竖直梁传感器实物图Fig.4 A photograph of the sensor with four vertical beams

2.2 传感器静态力标定实验

使用80 mm×80 mm×15 mm工件，选择传感器载物台面及工件表面上的6个位置点分别进行力的加载实验，实验环境如图5所示。使用深圳三思UTM6104电子万能实验机施加静态力，使用美国福禄克8846A台式数字万用表对测量电路的电压输出进行测量，使用台湾固纬GPS-3303C稳压电源对测量电路提供5 V直流供电。为更准确地测量传感器的输出值，使用美国德州仪器INA128芯片分别对输出信号进行放大，测量电路X，Y和Z的放大倍数约为99，99和209。

图5 传感器静态力受力实验Fig.5 Sensor static force loading test

利用ANSYS软件估算静态力的施力范围，在工件角点上施加三轴向分量分别为60 N的外力时，工件水平和竖直方向上的最大位移为19.60 μm。因此，静态力施加范围为0 ～ 60 N，加载的单向静态力的大小先线性增加，再线性减少，变化步长为6 N，力保载时间为25 s，每个位置点进行3次实验，以3次测量得到的数据平均值进行计算。

2.2.1 传感器的偏心输出误差

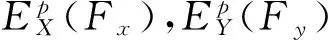
(p=2,3,…,6;Fi′=6,12,…,60)

(7)

其中：ΔU为输出电压和无加载时相比的变化量；p为施力点的位置；i=X则i′=x;i=Y则i′=y;i=Z则i′=z。

如图6所示，当外力作用点在距传感器上板面中心35 mm×35 mm×15 mm的空间范围内移动时，传感器测量电路主测量分量的输出变化不超过4.98%，交叉干扰分量输出变化不大于3.69%。参考现阶段对固定式三维铣削力传感器的解耦研究，当受力点位置变化时，四直筋式测力仪交叉干扰不超过4%[9]，十字梁铣削力传感器输出信号偏差最大不超过5.60%[10]。因此，优化尺寸后的竖直梁固定式铣削力传感器在抑制铣削位置变化对输出信号产生的影响上具有一定的实用价值。

2.2.2 传感器的静态解耦误差

利用最小二乘法将所有测量数据进行线性拟合，得到传感器的解耦矩阵如式(8)所示，输出电压单位为mV。将在相同受力位置、受相同大小的单向力作用时的传感器三路输出电压分别相加，作为UX，UY和UZ，使用式(8)进行矩阵解耦。将力分量数值与万能实验机施加的标准静态力比较，误差如图7所示，最大解耦误差不超过5.58%。

(8)

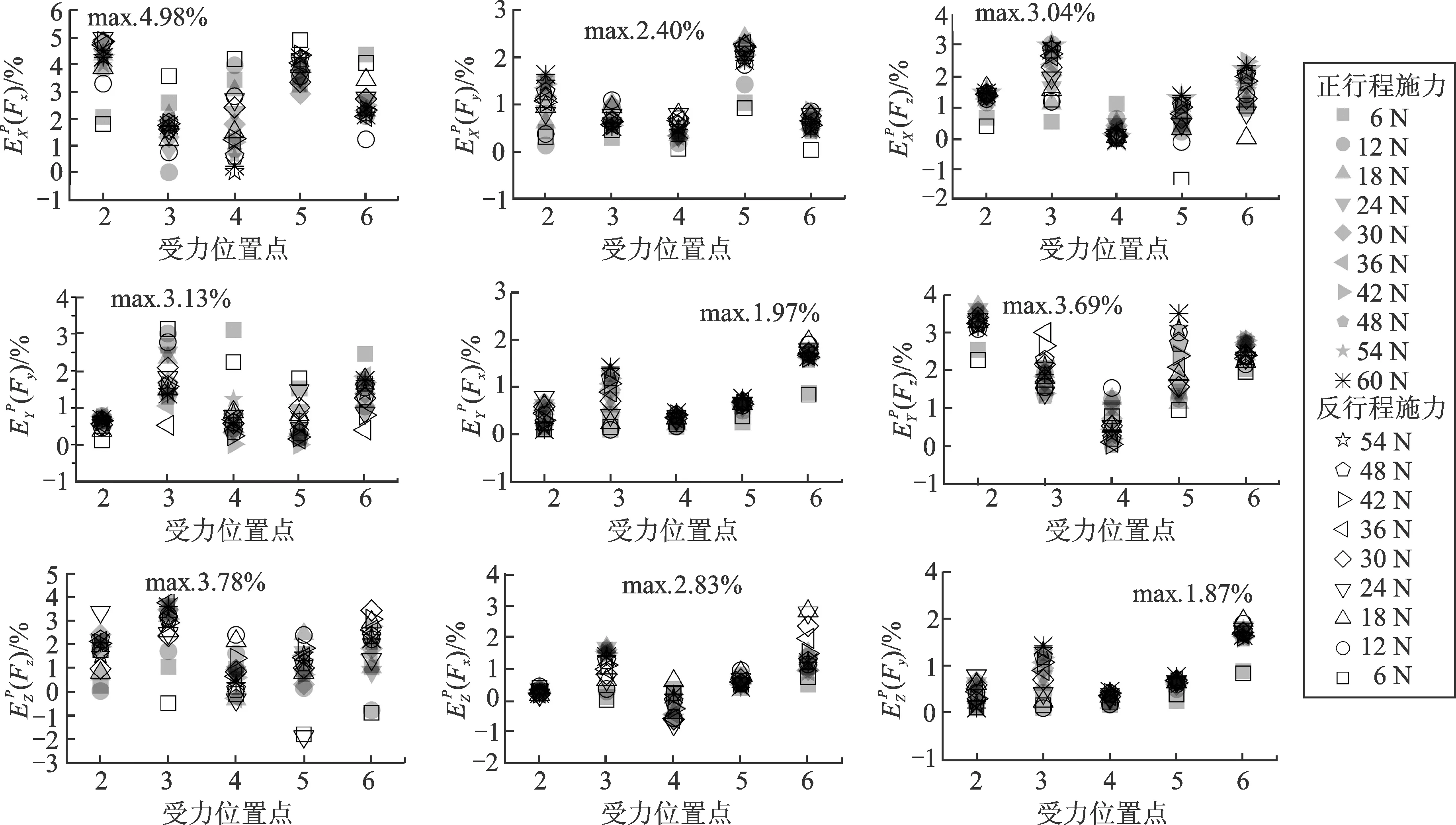
图6 静态受力情况下的测量电路输出误差Fig.6 Errors of measuring circuits under static forces

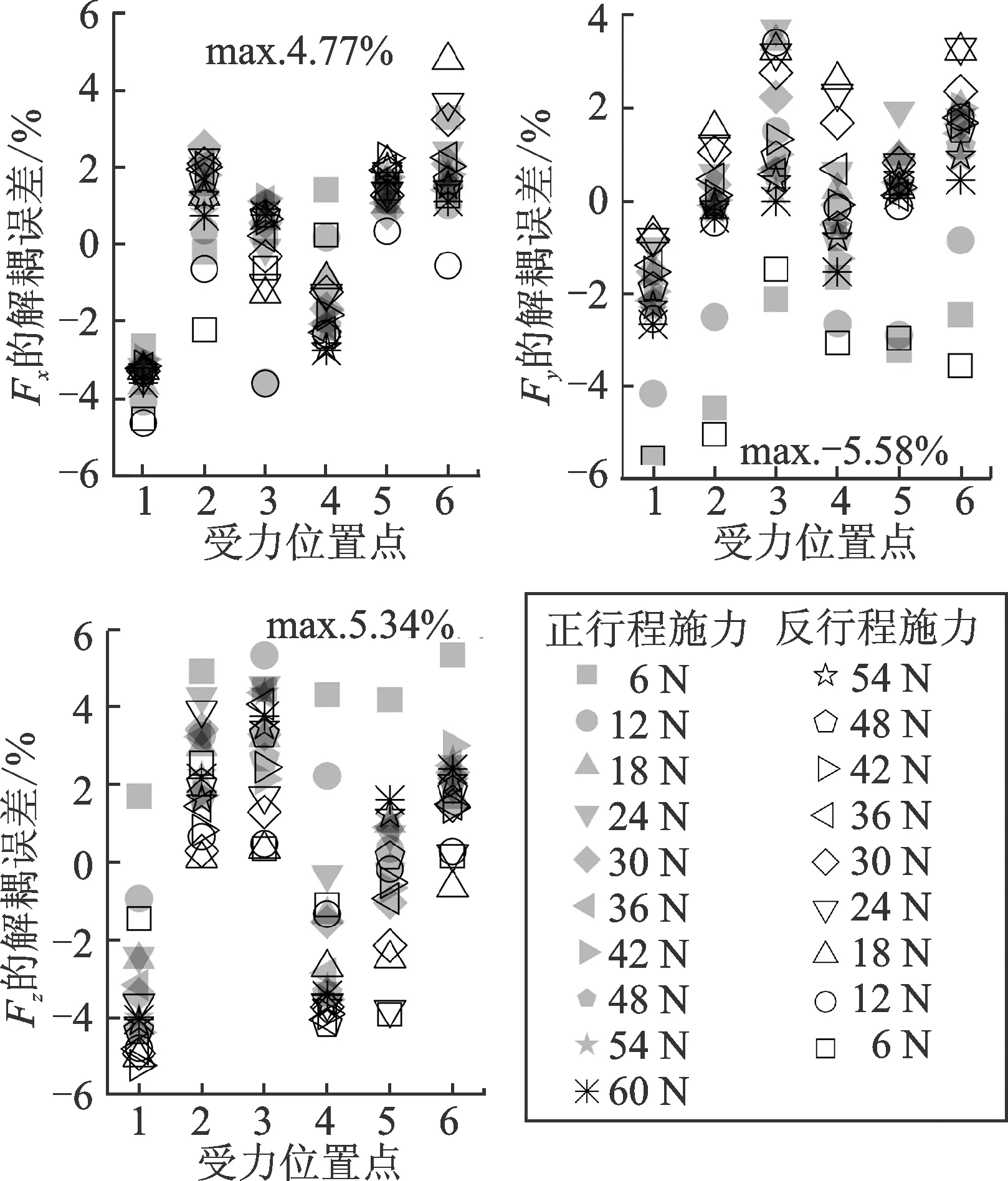
图7 传感器受力位置点1～6处的解耦误差Fig.7 Sensor decoupling errors for force applied points 1～6

由于基于时域的铣削力刀具磨损判别方法多通过观察切削力平均值的相对增长趋势实现，且当刀具出现磨损时，平均铣削力增长速度极快。例如，在微铣削力加工中，当直径为2 mm、铣刀磨损约0.04mm时，Fx和Fy分别增长约3.18和3.25倍[12]。因此，笔者研发的竖直梁固定式铣削力传感器在解算精度上基本可以满足铣削过程在线监测系统的要求。另外，若将解耦矩阵使用软件算法进行优化，得到的测力仪解耦误差可能更小，这里不再进一步讨论。

3 传感器铣削实验

3.1 传感器动态解耦矩阵的确定

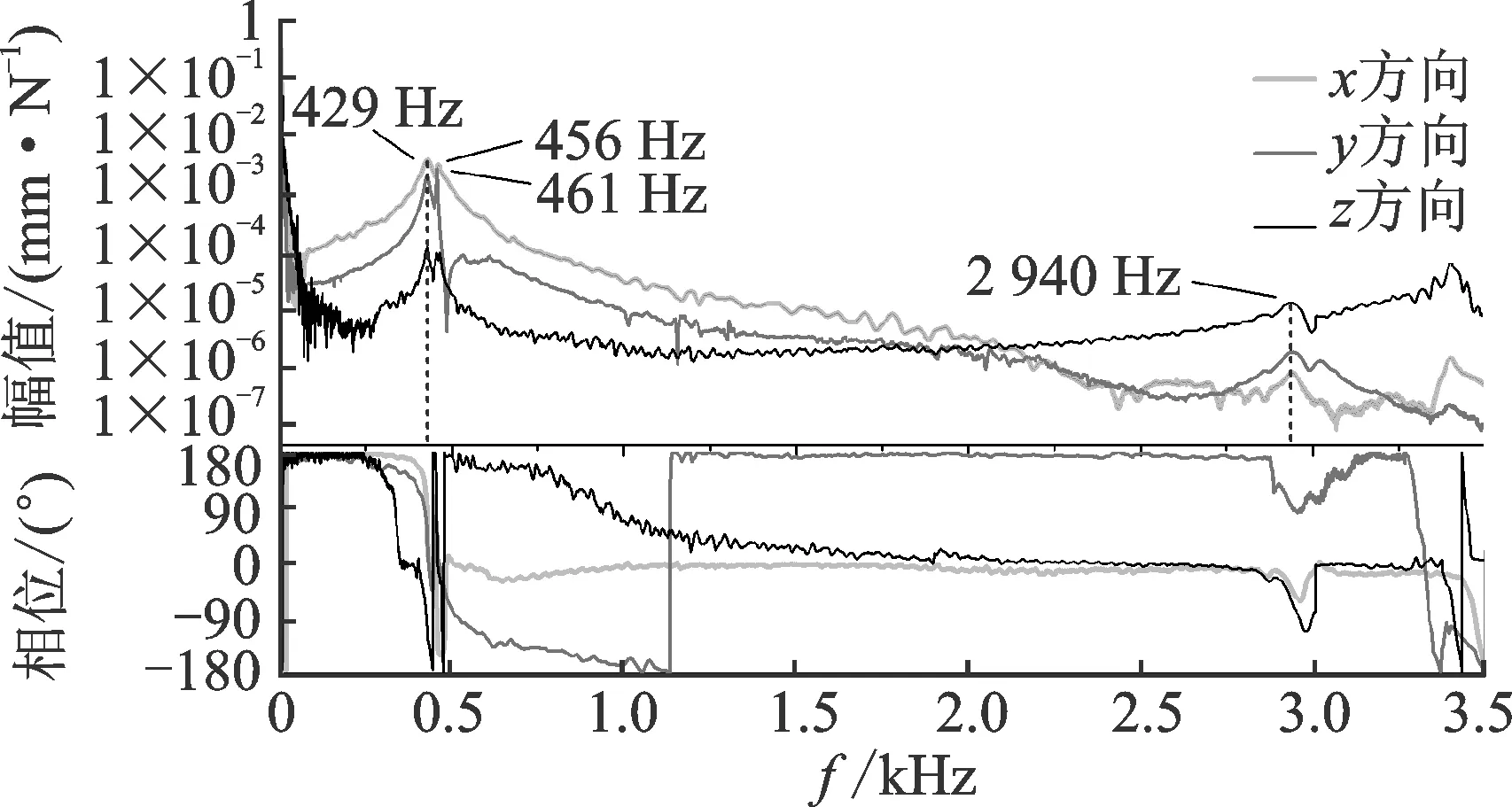
图8 传感器弹性梁中点的位移频响曲线Fig.8 The frequency response curves of the displacement of the elastic beam midpoint

测量时，在传感器上夹持80 mm×80 mm×15 mm的45号钢质工件，使用美国PCB 086E80力锤分别沿水平和竖直方向敲击工件，将PCB 356A66压电型加速度计分别粘贴在传感器弹性梁侧表面的中点和轴线上端点处，通过德国西门子SCADAS305移动数据采集系统对力和加速度信号进行采集和处理。图8为在梁中点处测得的三向位移频响曲线。在梁端点测得的频响曲线与该图相似，这里不再绘出。如图8所示，传感器的一阶共振频率约为429 Hz。当铣削激励信号远小于共振频率时，忽略压电型传感器低频测量的误差，测得的加速度计位移幅频特性曲线均小于1，且相频特性曲线与0 Hz时基本一致。当使用静态力标定矩阵替代动态力标定矩阵对铣削数据进行解耦时，几乎不影响求解出的力分量间的相对比例关系。在不考虑工件质量变化的情况下，由于测量结果是通过振动系统间接得到的，传感器实际所受铣削力将与该解耦结果近似呈线性关系。

3.2 传感器铣削实验

铣削实验环境如图9(a)所示，选用直径d0为16 mm的三刃高速钢立铣刀以顺铣方式沿x方向进行切削。传感器电压输出使用美国泰克MSO4104示波器进行记录，采样频率不小于10 kHz，所得信号经过400 Hz低通滤波器滤波。图9(b)中①～④为实验中的切除部分，铣削出的台阶贯穿整个工件。4组实验铣削参数如表3所示。其中，实验1与实验2,3和4的铣削参数相同，但加工位置不同。编辑加工步骤时，尽量保证实验1和实验2，3和4间的工件质量相差较小。

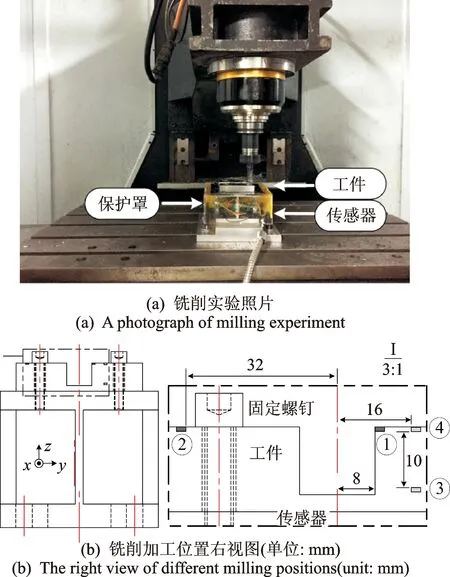
图9 传感器铣削实验Fig.9 Sensor milling experiment

使用式(8)的解耦矩阵求解被测力，实验1和3的铣削力时域波形和Fx的频谱图如图10所示。刀刃产生的激励信号的频率可以从图中读出，由于实验2与实验1波形近似，实验4与实验3波形近似，其余图形不再一一列出。以各组实验中进入稳定铣削状态下的数据为基础，将主轴旋转周期内的峰峰值平均，计算结果如表4所示。

表3 铣削实验参数Tab.3 Milling parameters in experiments

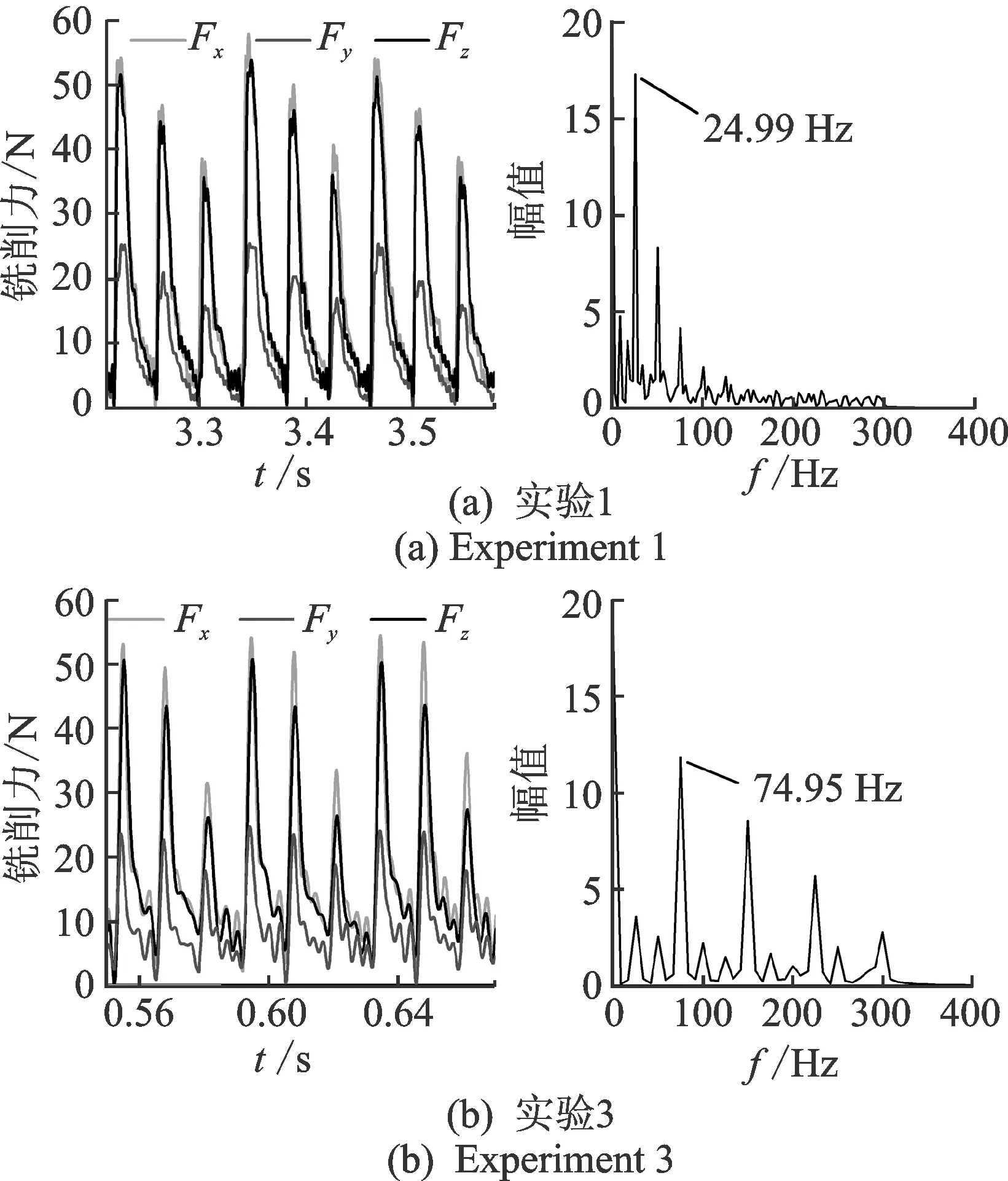
图10 铣削力时域和频域图Fig.10 Milling forces in both time and frequency domain

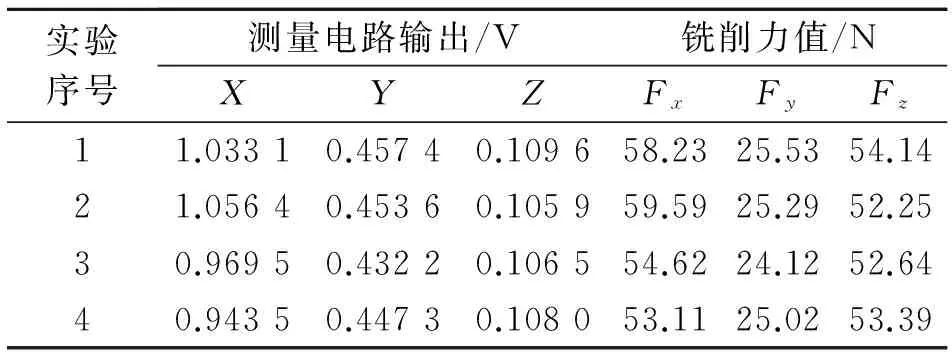
表4 铣削实验结果Tab.4 The results of milling experiment

根据高速钢铣刀铣削碳钢的经验公式[13]，Fx与Fy的比值约在2～2.57(0.8/0.4～0.9/0.35)之间，Fx与Fz的比值约在1～1.2(0.8/0.8～0.9/0.75)之间。根据表4的测量数据，Fx/Fy和Fx/Fz的计算结果如表5所示。解耦得到的铣削力分量间的比值与理论值基本相符，证明了解耦方法的正确性。

根据表4，将实验1与实验2，3，4的测量结果进行对比。分别以实验1和3的数据作为基准，传感器在不同铣削位置处测得的力分量的差值如表6所示。以中心点为基准，在水平等效相距24 mm或竖直相距10.75 mm的不同位置处切削，传感器测得数据的最大偏差为3.73%。这再次证明了当偏心外力作用在工件上时，笔者提出的竖直梁结构三维铣削测力仪可以减弱其对输出信号的影响。

表5 铣削力分量测量值比值Tab.5 The ratio of measured milling force components

表6 不同铣削位置间的测量量差值Tab.6 Output differences between milling positions

4 结束语

设计了一种应变型固定式竖直梁结构三向铣削测力仪，可以有效抑制由于铣削过程中受力点的偏移对传感器输出信号造成的影响。从理论上阐明了当受力点在一定空间范围内移动时，测力仪通过应变片串联可以直接消除大部分情况下的输出信号变化，通过尺寸优化可以将其余情况下的输出变化维持在可用范围内。利用静态力测量实验和动态铣削实验分别验证了传感器设计的可行性。静态施力实验中，当受力点维持在距传感器载物台面中心35 mm×35 mm×15 mm范围内时，传感器最大解耦偏差为5.58%。在工件上水平等效相距24 mm或竖直相距10.75 mm的不同位置处切削，传感器的铣削力信号峰峰值最大相差3.73%。本研究为解决竖直方向高刚度的应变型固定式铣削测力仪的解耦问题提供了新的思路和参考。

[1] Saglam H,Unuvar A.Tool condition monitoring in milling based on cutting forces by a neural network [J].International Journal of Production Research,2003,41(7):1519-1532.

[2] 石莉，贾春德，孙玉龙.应用小波研究动态铣削力及预报铣削颤振[J].哈尔滨工业大学学报，2006，38(10):1778-1780.

Shi Li,Jia Chunde,Sun Yulong.Research on dynamic milling force with wavelet analysis and forecasting milling chatter[J].Journal of Harbin Institute of Technology,2006,38(10):1778-1780.(in Chinese)

[3] Chen C H,Wang Y C,Lee B Y.The optimal design of micro end mill for milling SKD61 tool steel[J].International Journal of Advanced Manufacturing Technology,2013,68:165-173.

[4] Zhang Huiping,Li Zhenjia,Zheng Minli,et al.Cutting tool path choice based on the fluctuation of cutting force in NC milling[C]∥Proceedings of the 9th International Symposium on Advances in Abrasive Technology.Dalian:Trans Tech Publications Ltd,2007:441-446.

[5] Rizal M,Ghani J A,Nuawi M Z,et al.A review of sensor system and application in milling process for tool condition monitoring[J].Research Journal of Applied Sciences,Engineering and Technology,2014,7(10):2083-2097.

[6] 黄震，赵威.高频响铣削测力仪结构设计与试验研究[D].南京：南京航空航天大学，2014.

[7] Zhao You,Zhao Yulong,Liang Songbo,et al.A high performance sensor for triaxial cutting force[J].Sensors,2015,15(4):7969-7984.

[8] 许林云，刘军，李赵春.八角环三向测力传感器的研究[J].南京林业大学学报：自然科学版，2008，4：121-124.

Xu Linyun,Liu Jun,Li Zhaochun.Study on triaxial forces sensor of octagonal ring[J].Journal of Nanjing Forestry University:Natural Sciences Edition,2008,4:121-124.(in Chinese)

[9] 袁俊哲,冯玉成,任玉伦.铣削测力仪[J].哈尔滨工业大学学报,1977,4:27-47.

Yuan Junzhe,Feng Yucheng,Ren Yulun.Milling dynamometer[J].Journal of Harbin Institute of Technology,1977,4:27-47.(in Chinese)

[10]Li Yingxue,Zhao Yulong,Fei Jiyou,et al.Development of a tri-axial cutting force sensor for the milling process[J].Sensors,2016,16(3):1-23,405.

[11]褚家麟.机床测力仪的标定及使用(CIRP推荐资料) [J].振动、测试与诊断，1983,4:46-57.

Chu Jialin.Calibration and application of machine tool dynamometer (CIRP recommended resource) [J].Journal of Vibration,Measurement &Diagnosis,1983,4:46-57.(in Chinese)

[12]赵显日.刀具磨损对微铣削力变化影响的理论与试验研究[J].组合机床与自动化加工技术,2015,7:19-22.

Zhao Xianri.Study on the variation of micro milling forces and specific cutting forces with tool wear[J].Modular Machine Tool and Automatic Manufacturing Technique,2015,7:19-22.(in Chinese)

[13]陆建中，孙家宁.金属切削原理与刀具[M].4版.北京：机械工业出版社，2005：161-163.

10.16450/j.cnki.issn.1004-6801.2017.04.001

* 国家杰出青年科学基金资助项目(51325503)

2016-12-13

TP212

赵玉龙，男，1968年3月生，教授、博士生导师。现为长江学者特聘教授、科技部中青年科技创新领军人才、国家自然基金委杰出青年基金、国务院特殊津贴专家、国家“百千万人才”和国家中青年突出贡献专家。主要研究方向为MEMS技术、传感器技术及微纳制造领域基础理论和工程应用。曾发表《A novel high temperature pressure sensor on the basis of SOI layers》(《Sensors and Actuator,A Physical》2003,Vol.108)等论文。 E-mail：zhaoyulong@mail.xjtu.edu.cn