室内光环境质量的模糊综合评价方法研究

王秀华，付保川，吴宏杰

（1.苏州科技大学 数理学院，江苏 苏州 215009；2.苏州科技大学 电子与信息工程学院，江苏 苏州 215009）

室内光环境质量的模糊综合评价方法研究

王秀华1，付保川2*，吴宏杰2

（1.苏州科技大学 数理学院，江苏 苏州 215009；2.苏州科技大学 电子与信息工程学院，江苏 苏州 215009）

针对原有室内的照明质量评价中存在的概念划分不明确的问题，将模糊综合评价方法应用到室内光环境质量评价中，构建出基于模糊综合评价的评价模型。根据学校建筑照明标准，选取相关评价因素并对室内照明质量划分成等级，通过选择合理的隶属函数构建单因素评价矩阵，并利用评价因子权重系数方法，构建了基于模糊综合评价的室内光环境质量评价模型。将该模型应用于室内的照明系统并对其进行评价，测试结果表明，基于该评价模型的评价结果与实际情况相吻合，从而说明了该评价方法的有效性。

室内光环境；模糊综合评价；隶属函数；权重系数

良好的光环境是视觉健康的有力保障。据统计，人的一生中80%以上的时间是在室内度过，且87%的信息则是通过视觉神经系统来获取的[1]，因此，室内光环境质量对信息获取尤为重要。

室内光环境是指与空间形状有关的光照（照度水平和分布、照明的形式）和颜色（色调、色饱和度、室内颜色分布、颜色显现）对生理和心理产生的影响。而光环境评价则是对室内光照及颜色进行一系列复合分析研究及评估，从而确定光环境的质量优劣。

目前，关于室内照明评价的方法主要有以下几种[2]：（1）主观评价法。主观评价法是荷兰费舍教授等学者根据人的心理感受提出了用视觉满意度曲线评价室内照明水平的方法。该方法主要是指专家评定法，其基本思想是通过评定者的主观意愿决定整个评价过程，其缺点在于评价的随机性较大。（2）因素分析法。因素分析法是同济大学杨公侠教授应用试验心理学中量表法提出。它是利用数学方法对观察到照明过程中出现的情况进行由此及彼的处理，并且得到影响照明的本质因素。该方法可以使复杂的研究课题简单化并且保持其基本的信息量。但是该方法忽略了各因素之间的关联性。（3）行为观察法。行为观察法同样是杨公侠教授应用试验心理学中量表法提出的。其基本思想是指评价者在自然条件下有目的、有计划地通过直接观察并记录被评价对象的行为外部表现，以此作为判断被评价对象的资料。其缺点在于评价者得到的观察结果容易受自身生理限制和主观意识影响，从而导致该方法不能真实反映室内照明的质量状况。行为观察法的因素分析法是一种客观的数学程序，但是它并没有完全摆脱主观判断的思想。（4）模糊数学法。中国建筑科学院物理研究所肖辉乾教授、张耀根教授，重庆大学陈仲林教授及湖北孝感学院王建华副教授分别利用模糊数学方法对照明光环境进行了评价。该方法考虑了室内光环境质量等级界限的内在模糊性，但是在评价过程中数据往往是由评价者人为给定的，并非精确测量给出的，因此，评价结果主观性较强。室内光环境评价因子的评判集在概念上具有较大的模糊性，在判断过程中往往给不出非此即彼的明确划分[3]。对于这种概念界限划分不明确的事物可以借助模糊综合评价法进行评判。笔者将应用模糊综合评价的方法对室内光环境进行评价。

1 模糊综合评价方法

模糊综合评价法就是按照给定的标准，通过模糊变换对某类事物中的各个因素分别进行单一评价，然后通过众多的单一评价对此类事物进行整体评价，这种方法称为模糊综合评价。模糊模型已经成功的应用到了多个领域[4]，但要注意的是在评价过程中要考虑各因素在整体评价中所占的权重。其具步骤如下[5]：

（1）确定模糊综合评价对象的因素集 U＝{u1，u2，…，un}，其中 ui（i=1，2，…，n）代表对评价对象起作用的因素。

（2）给出评判集 V＝{v1，v2，…，vm}，其中 vj（j=1，2，…，m），表对该事物品质的 m 种不同等级的划分。

（3）单因素评价。即建立一个从U到V的模糊映射

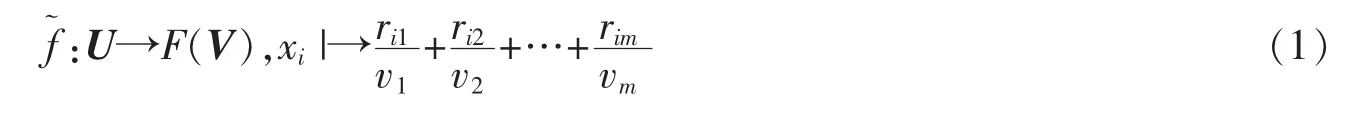
其中，0≤rij≤1，i=1，2，…，n；j=1，2，…，m。 rij是第 i个评价因素对第 j种评价等级的隶属度。

表示，R为单因素评价矩阵。

（4）确定权重集A＝{a1，a2，…，an}。其中，ai表示第i个评价因素在模糊综合评价过程中所占的影响比重。

（5）模糊综合评价。即将模糊权重集A与单因素评价矩阵R进行模糊关系合成得到模糊综合评判矩阵B。

其中，bj（j=1，2，…，m）表示这类事物达到第 j种评判等级的程度。其评价结果是 bj（j=1，2，…，m）中的最大值。

2 室内光环境质量模糊综合评价模型

2.1 确定评价对象因素集

影响室内照明质量的因素主要有照度水平、亮度分布、光色、显色性、眩光、透光方向和造型立体感等。这些因素取值的不同直接影响到室内照明质量的优劣。根据学校建筑标准，文中将着重选取照度水平、显色性、统一眩光值作为评价对象的因子，构成评价因素集 U＝{μ1，μ2，μ3}。

2.2 确定评语集

室内照明质量分级是室内照明质量评价的基本依据。根据GB50034-2013《建筑照明设计标准》，将教室一般照明的照度、显色性（Ra）和统一眩光值（UGR）划分为三级。其中，一级表示照明质量好，二级表示照明质量中等，三级表示照明质量差。 于是得到评价集 V＝{v（好），v（中等），v（差）}。 简记为 V＝{v1，v2，v3}。

在学校照明中，照明评价主要是从课桌面照度、显色性和统一眩光值三个方面进行评价的。其中，学校教室的照度值一般为100～300 lx。光的显色性是指照明光源对物体色表的影响。人工光源用Ra作为评价显色性的指标。光源的显色性指数越高，它的显色性越好，与参照光源一样，其显色指数为100。一般认为Ra=80～100显色性优良，Ra=50～79显色性一般，Ra＜50显色性差。1995年国际照明委员会（CIE）提出了统一眩光值（UGR）的概念作为评价不舒适眩光的定量指标。不同的值对应着不同的不舒适眩光感受，见表1。

表1 不同值对应着不同的不舒适眩光感受

对于学校状况，我国提出了学校建筑照明标准值，见表2。

表2 教育建筑标准值

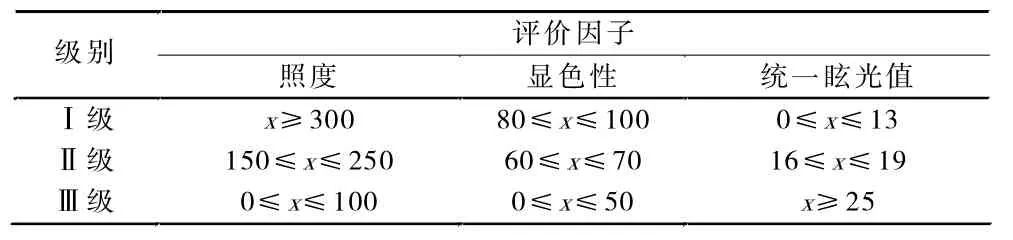
表3 室内照明质量分级

依据目前我国有关室内照明质量分级标准，构成评语集 V={v1，…，vm}，vi↔yi0。 设评价对象集为 P={p1，…，pl}，pk↔xk0，其中，yi0=（yi0（1），…，yi0（n）），xk0=（xk0（1），…，xk0（n）），yi0（j）表示等级 i中第 j种影响因素的标准值，xk0（j）表示第k个评价对象的第j种影响因素的检测值。室内照明质量等级划分见表3。

2.3 数据标准化

由于各指标的含义及目的不同，因此，指标值通常具有不同的量纲和数量级，为了消除量纲和数量级不同带来的不可对比性，使各指标之间具有可比性，需对原始数据进行标准化处理。采用初始化算子对各因素序列进行量纲统一的量化处理，其具体计算公式为

其中，xk0（j）表示第k个评价对象的第j种评价因子的检测值，s（j）表示评价标准序列中第j种评价因子的标准值，xk（j）表示标准化后第k个评价对象的第j种评价因子的标准值。

2.4 构建模糊关系矩阵

2.4.1 评价因子隶属关系的确定

隶属度是描述评价因子与评价等级之间的相关程度的参数[6]。由于确定照明质量是一个模糊的概念，照明质量分级标准也是模糊的，所以采用隶属度（rij）来划分界限。

在计算评价因子隶属度时，需要选择一个合适的隶属度函数，文中选用体型隶属度函数[7]，其具体公式如下：

（1）偏小型

（2）中间型

（3）偏大型

在式中：（1）用来计算偏小型的隶属度函数；（2）用来计算中间型的隶属度函数；（3）用来计算偏大型的隶属度函数。 其中 ai（i=1，2，3，4）为参数，对应不同的因素取不同的 ai。

2.4.2 构建模糊关系矩阵

根据教室内照明的实际情况，计算相应的照度水平、统一眩光值和检测光源的显色性。代入上面的隶属函数中去，就能得到相应的隶属度[8]。

对室内照明因素集U={照度μ1，显色性μ2，统一眩光值μ3}中每一个因素进行单因素评判，然后将会在评判集 V={v（好），v（中等），v（差）}中得到一组相应的数据。 例如，对于得到的照度值 μ1，通过上述隶属函数可以求得它隶属于 v（好）的隶属度为 r11，隶属于 v（中等）的隶属度为 r12，隶属于 v（差）的隶属度为 r13。 即

类似地，可以得到

因此，可以建立相应的模糊评价矩阵R。R是各个评价因子到各个等级隶属度的一种转换。即得到

2.5 确定评价对象权重集

在复杂的评价过程中，需要考虑的因素往往很多，因素还分为不同的层次，这时，应用模糊综合评判的单级模型，因素权重的分配很难合理[9]，权重矩阵要考虑各评价因子在总体中的地位，确定评价因子的权重是衡量参与评价的各个因子之间对室内照明质量影响的相对重要程度，根据各因子对室内照明质量的影响分别给予不同的权重值[10]。因此，需要将各单因子的实测值和给定的标准值分别代入权重计算公式，即可得到各单因子的权重，即因子权重集 A＝{a1，…，an}。其中，ai（i=1，2，3）表示对应的各项评价因子的重要程度。在模糊综合评价中，给出了很多赋权方法。文中将采用指数超标法求各个因子的权重。光环境质量分数指数

2.6 确定模糊综合评价结果向量

当模糊关系矩阵R和权重模糊矩阵A确定后，可以通过最大-最小合成运算[11]得到模糊综合评价矩阵B，即 B=A◦R。 根据最大隶属度原则，取 bj=max（b1，b2，…，bn）∈B，那么该评价对象级别属于第 j级。

3 实例验证

笔者以苏州科技大学某教室为例进行研究。该教室长 12.3 m，宽 7.7 m，高 3.3 m，室内共有 9排 11列课桌，课桌高0.75 m，现按标准将教室分为9个区域。室内均匀分布着16套36 W的T8荧光灯（根据北京松下照明公司提供的数据可知该T8荧光灯的显色指数为85），灯距桌面 2.5 m。

下面按表4中工况对各个区域内的照度进行测量。

通过2016年11月15日上午10：45-12：25之间的测量可以得到照度实测值见表5。

表4 工况表

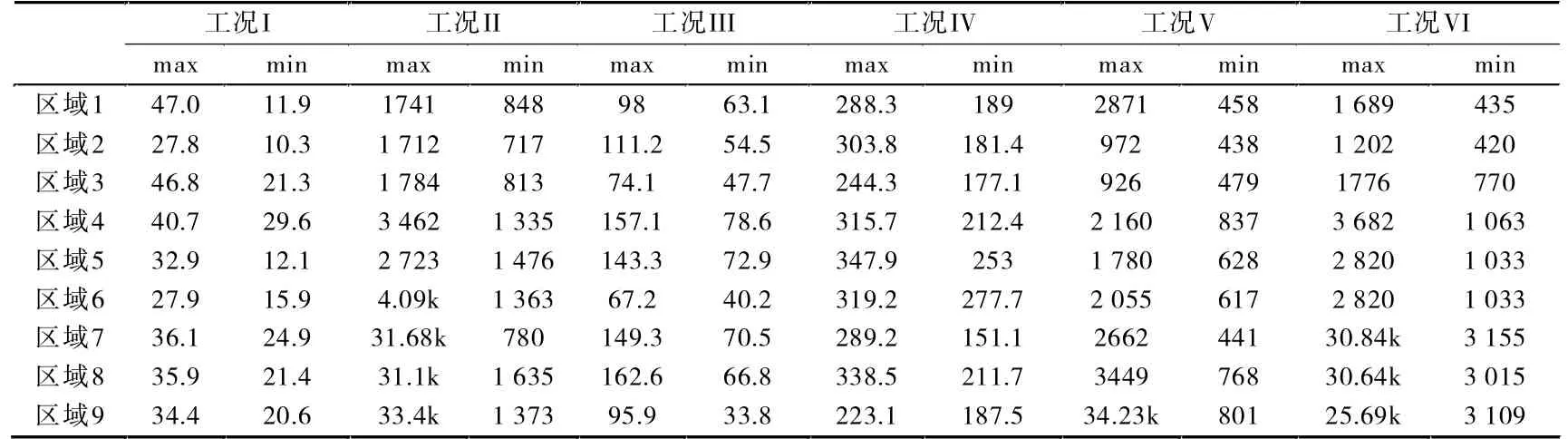
表5 照度实测值（单位：lx）

通过测量及计算可得：工况Ⅰ的室内最小照度为10.3 lx，最大照度为47.0 lx，平均照度为27.6 lx。工况Ⅱ的室内最小照度为717 lx，最大照度为33.4k lx，平均照度为1 520.9 lx（除去三个太阳直射处的测量值）。工况Ⅲ的室内最小照度为33.8 lx，最大照度为162.6 lx，平均照度为88.16 lx。工况Ⅳ的室内最小照度为151.1 lx，最大照度为347.9 lx，平均照度为250.6 lx。工况Ⅴ的室内最小照度为438 lx，最大照度为34.23k lx，平均照度为1 373.06 lx（除去一个太阳直射处的测量值）。工况Ⅵ的室内最小照度为420 lx，最大照度为30.84k lx，平均照度为1 870.67 lx（除去三个太阳直射处的测量值）。选取适当的参数分别关于照度、Ra和UGR的梯形分布隶属函数图像如图1。

图1 分布隶属函数图像

其中，图 1（a）、图 1（d）和图 1（g）是隶属于一级的图像，图 1（b）、图 1（e）和图 1（h）是隶属于二级的图像，图 1（c）、图 1（e）和图 1（i）是隶属于三级的图像；图 1（a）、图 1（b）、图 1（c）分别是关于照度的偏大型、中间型和偏小型隶属度函数图像，此处取 a1=100，a2=150，a3=250，a,4=300；图 1（d）、图 1（e）、图 1（f）分别是关于 Ra的偏大型、中间型、偏小型梯形隶属度函数图像，此处取 a1=50，a2=60，a3=70，a,4=80；图 1（g）、图 1（h）、图 1（i）分别是关于UGR的偏小型、中间型、偏大型梯形隶属度函数图像，此处取a1=13，a2=16，a3=19，a,4=25。

文中主要讨论工矿Ⅳ，根据上文可知，工矿Ⅳ的平均照度为250.6 lx，显色指数（Ra）为85，通过统一眩光值公式求得该教室内的统一眩光值为14.6[12]。将照度值250.6 lx代入图1（a），可以得到照度隶属于一级的隶属度为0.012，代入图1（b）可以得到照度隶属于二级的隶属度为0.988，代入图1（c）可以得到照度隶属于三级的隶属度为 0；同理，将显色指数（Ra）为 85 分别代入图 1（d）、图 1（e）、图 1（f）分别得到相应的隶属度为 1、0 和 0；把统一眩光值（UGR）为 14.6 代入图 1（g）、图 1（h）、图 1（i）分别得到相应的隶属度 0.53、0.47 和 0。

通过上述隶属度可以得到单因素评判矩阵

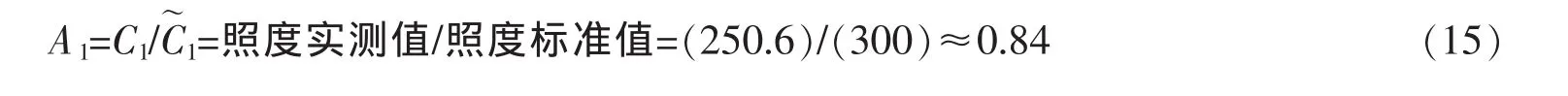
类似地，可以得到

通过公式（13）对各个单项权重进行归一化处理，即

可以求得

即得出权重集为

根据因素集对室内照明质量影响权重A和总体隶属函数模糊关系矩阵R，将A和R进行复合运算，采用加权平均型评价.得到综合评判结果[13]。即公式（3）

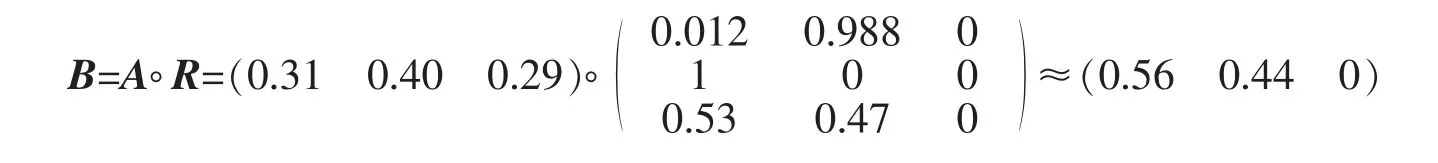
根据最大隶属度原则，在室内照明质量评价时，选取最大的bj作为对应的评价等级。很显然，maxbi=b1，由评价结果可以得出该教室内的照明质量较大程度上隶属于一级，并且在一定程度上隶属于二级。

根据上述方法，可以分别计算出该教室9个区域的模糊综合评价结果见表6。

根据9个区域的模糊评价结果可以得到图2。

根据图2很显然可以得到室内各个区域的光环境质量都隶属于一级，同时，可以看出各个区域之间的光环境质量是存在细微差别的，根据隶属于一级值的不同，对9个区域按照从大到小进行排列得到：区域5＞区域6＞区域 8＞区域 4＞区域 9＞区域3＞区域7＞区域1＞区域 2。因此，可以得到该教室区域5、区域6的照明质量相对于其他几个区域更好一些。

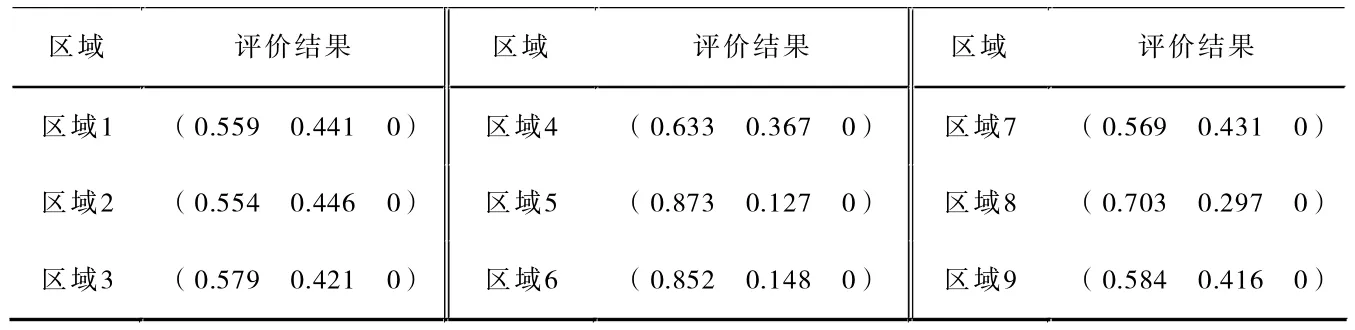
表6 区域的模糊综合评价结果

图2 各区域模糊综合评价结果

4 结语

目前对于照明评价的方法有多种。但是相比较于以往其他方法，模糊综合评价法的评价结果更能够真实客观的反映照明质量的实际情况，并且该方法简单可行便于推广。光环境评价过程中影响因素众多，模糊综合评价方法能够很好的综合各个因素之间的权重关系对光环境进行合理准确的判断。通过运用模糊综合评价方法对室内光环境评价进行建模，并应用到某大学教室进行实例验证，对得到的最终结果进行综合分析，其测试结果表明，所测数据与教室的客观实际情况相吻合。

[1]黄晨.建筑环境学[M].北京：机械工业出版社，2007.

[2]王书晓.办公室光环境评价体系研究[D].北京：中国建筑科学研究所，2007.

[3]LI Y.Study on Fuzzy mathematics and its applications[J].International Conference on Advances in Mechanical Engineering&Industrial Informatics，DOI：10.2991/ameii-16.2016.25.

[4]ZHANG B，WANG J，ZHANG J.Dynamic model of reheating furnace based on fuzzy system and genetic algorithm[J].Control Theory&Applications，2003，20（2）：293-296.

[5]梁保松，曹殿立.模糊数学及其应用[M].北京：科学出版社，2007.

[6]梁淑轩，吴虹.环境空气质量动态变化规律的模糊数学综合评价[J].干旱区资源和环境，2010，24（6）：77-81.

[7]杨晓艳，鲁红英.基于模糊综合评判的城市环境空气质量评价[J].中国人口·资源与环境，2014，24（5）：143-146.

[8]LI Menglong，MA Weiping.Research on Fuzzy mathematics-based evaluation system of gyms in colleges and universities[J].International Journal of Digital Content Technology and its Applications，2012，6（7）：110-118.

[9]杨苹，杨俊华，吴捷.变权重模糊综合评判模型及其在故障诊断中的应用[J].控制理论与应用，2000，17（5）：707-710.

[10]张淑琴，白艳丽，张洪林.模糊数学在室内空气质量评价中的应用[J].环境科学与管理，2006，31（9）：188-189.

[11]谢季坚，刘承平.模糊数学方法及其应用[M].武汉：华中科技大学出版社，2013.

[12]北京照明学会照明设计专业委员会.照明设计手册[M].北京：中国电力出版社，2013.

[13]陈仲林，奚于成.建筑光环境评价方法[J].重庆建筑工程学院学报，1993，15（3）：35-39.

Fuzzy comprehensive evaluation method for indoor light environment quality

WANG Xiuhua1， FU Baochuan2*，WU Hongjie2
（1.School of Mathematics and Physics，SUST，Suzhou 215009，China；2.School of Electronic&Information Engineering，SUST，Suzhou 215009，China）

In order to solve the unclear division of concepts in the evaluation of indoor lighting quality,we applied the fuzzy comprehensive evaluation method into the evaluation of indoor light environment quality and constructed a model based on this method.According to the standard of school building lighting,we selected relevant factors and graded the indoor lighting quality.Through the selection of membership functions,we constructed single factor evaluation matrix.Then with the evaluation factor weight coefficient method,we constructed the indoor light environment quality evaluation model based on fuzzy comprehensive evaluation.The application of this model shows that the actual situation and the evaluation result based on this model are consistent,which proves the effectiveness of this evaluation method.

indoor light environment；fuzzy comprehensive evaluation；membership function；weight coefficient

O29 MR（2010）Subject Classification：00A69

A

2096－3289（2017）03－0030－07

责任编辑：谢金春

2017－01－10

国家自然科学基金资助项目（61672371）；江苏省住房城乡建设厅科技项目（2016ZD49）；苏州科技大学科研基金资助项目（XKQ201517）

王秀华（1990-），男，山东潍坊人，硕士研究生，研究方向：工程中的数学技术。

*通信作者：付保川（1964-），男，博士，教授，硕士生导师，E-mail：fubc@163.com。