集装箱船全航线智能预配问题研究*
2017-09-11汪圆圆陈顺怀
汪圆圆 陈顺怀
(高性能船舶技术教育部重点实验室 武汉 430063)
集装箱船全航线智能预配问题研究*
汪圆圆 陈顺怀
(高性能船舶技术教育部重点实验室 武汉 430063)
针对挂靠多港口集装箱船的全航线预配问题,以倒箱量最少、船舶纵向强度最优为目标,提出该问题的0-1整数规划模型.利用基于规则的方法,并分别采用混合整数规划算法、蚁群算法和遗传算法求解之.结果表明,在待配载箱数较少时,混合整数规划算法快速,且得到的解为最优解.给出了基于以上三种算法及一定的装箱规则的全航线智能配载算法.采用该算法模拟计算得出了8 Bay集装箱船全航线智能预配结果,保证了倒箱量为0,且考虑到了纵向强度目标,即集装箱重心距离船舯的距离最小.
集装箱船;预配;整数规划;遗传算法;蚁群算法
0 引 言
集装箱预配问题是一类较为复杂的组合优化问题,其求解的复杂度随集装箱所占Bay位数的增加而呈爆炸式增长,预配需考虑如何通过合理配载使船舶具有较合理的浮态并且使船舶重量合理分布,以保障船舶的快速性和结构强度的安全.多年以来,国内外学者对此问题进行了一系列的研究.
张维英等[1-3]提出首先将集装箱按货物种类、尺寸和目的港组成同类箱组,以同类箱组为处理单元,以倒箱数量最少、船舶载箱率最高及不同目的港集装箱占用Bay位数量最少为目标,以满足船舶纵向强度和吃水差要求为约束条件,采用超尺寸装箱完成集装箱在船上的纵向布置,并产生配载的总布置图.而后在预配的基础上,针对单一目的港集装箱和混合目的港集装箱Bay位,分别以初稳性高度最优及横倾力矩最小、倒箱量最少为目标,采用基于指派问题的禁忌搜索算法和隐式图启发式搜索算法进行求解.而其给出的全航线配载算例中,没有赋予每个集装箱重量,实际上得到的全航线配载结果是无意义的.
Ambrosino等[4]提出一种针对集装箱配载问题的分解启发式算法,将集装箱配载问题分为三个子问题,预配问题则相当于这三个问题中的第一个问题.其采用系统的配载优化策略,运用启发式搜索策略,在理论上解决了大型集装箱船的配载问题.Avriel等[5]将集装箱配载问题转换为图着色问题,并且证明了当Bay位列数大于4时,无能力约束倒箱问题为NP完全问题.但并未给出具体求解策略及相关算例.Araújo等[6]将Pareto前沿与聚类搜索算法相结合,提出一种Pareto聚类搜索算法(pareto clustering search,PCS),以倒箱量最少和船舶稳定性最优为目标,得到了在船舶挂靠不同数目的港口时,采用该算法得到的前沿要优于其他两种算法.Pacino等[7]提出一种能够快速产生近优配载计划的二步分解算法,采用混合整数规划模型,松弛整数约束,使整个解产生的时间小于330 s,且解的效果良好.孙俊清等[8]讨论了停泊多港口的集装箱运输班轮全航线配载问题,以船舶稳性为约束,倒箱量为目标,建立了0-1整数规划模型,并采用改进的遗传算法求解之.其优势在于其算法的设计,而其劣势在于对集装箱全航线配载问题模型的建立过于简单,没有考虑到重量的合理分布,这显然是不合理的.
本文将针对文献[3]中的算例进行修改和一定的拓展,以倒箱量最少、船舶纵向强度最优为目标(模拟算例未考虑吃水差),提出该问题的0-1整数规划模型,并分别采用混合整数规划算法、蚁群算法和遗传算法求解之.结果表明,在待配载箱数较少时,混合整数规划算法快速,且得到的解为最优解.给出了基于以上三种算法及一定装箱规则的全航线智能预配算法,最后采用该算法模拟计算得出了8Bay集装箱船全航线智能预配结果.
1 配载问题的数学模型
1.1 问题描述
预配即按船上Bay为装载单元,将集装箱按类别(如尺寸、目的港、不同种类箱等)组成同类箱组,以同类箱组为装载单元,采用合适的装箱算法确定同类箱组在船上纵向布置,完成配载的总布置图,见图1.

图1 箱位排布俯视图
在图1中,以L1,L2,…,Lm为箱位的纵向排布顺序,按自船首至船尾增序排列.其所包含的箱位数量分别为r1,r2,…,rm,距船舯的位置为x1,x2,…,xm,图中显示了TEU和FEU箱位的排布示意.
以t表示装箱矩阵,即
(1)
式中:tij为装载港为i,卸载港为j的集装箱数量,j>i,否则tij=0,并且装箱矩阵元素符合下述关系为
(2)
式中:tn为第n港的装箱量.
则问题可以描述为:将tn个集装箱配载入图1的m个Bay位中,其中这tn个集装箱可以分为若干个同类箱组,如何配载可使得所产生的倒箱量,即先卸载集装箱被后卸载集装箱压在下面的次数最少、船舶的纵向强度最优.
1.2 数学模型的建立
假设与装箱矩阵对应的重量矩阵为
(3)
式中:wij为装载港为i,卸载港为j的集装箱重量.设待配载同类箱组分别为1,2,…,n,集装箱船Bay位号从首至尾分别为1,2,…,m,则集装箱船预配问题即如何将这n个同类箱组配载至这m个Bay位中,使得倒箱量最少、结构强度最优.
在集装箱全航线配载过程中,将配载变量定义为cij,表示将第i个箱组装载于第j个Bay位,见表1.

表1 配载变量定义
在配载过程中,对于混装Bay位,将按照先卸载港后装,后卸载港先装的规则,从而保证不产生倒箱量.由此,给出如下集装箱全航线配载0-1整数规划模型为
(4)
(5)
(6)
(7)
wi≤[w] (i=1,2,…,m)
(8)
n≤m
(9)
ti≤ri(i=1,2,…,m)
(10)
upID≤downID
(∀BayID∈MixedBay)
(11)
ShiftNums≤[Nums]
(∀BayID∈MixedBay)
(12)
式(4)表示所有集装箱组对船舯的力矩越小越好,集装箱船的总纵强度以左右集装箱组对于船舯的力矩来表示,因此,该值越小,表示总纵强度越好.式(5)~(7)表示配载变量约束,即配载变量只能取0或者1之间的一个,且表1的任意一行、任意一列相加都要为1,即每一个箱组只能占用一个Bay位,每一个Bay位只能被一个箱组所占据.式(8)表示每一个Bay位所装载的集装箱重量不得超过该Bay所允许装载的集装箱最大重量.式(9)表示箱组个数不得超过集装箱船的Bay位总数.式(10)表示任意箱组中的集装箱数目不得超过其所占据的Bay位中的集装箱箱位数量.式(11)表示对于混合Bay,卸载港编号小的集装箱不得处于卸载港编号大的集装箱之下,即保证先卸载港的集装箱后装,后卸载港的集装箱先装.式(12)表示在整个装配过程产生的倒箱量不超过[Nums],本文模拟算例将之取为0.
2 全航线智能预配算法
目前,针对全航线配载问题的算法多基于经典装箱算法[9],以Bay位利用率、倒箱量为目标进行配载,而后校核强度、吃水差等约束条件.本文则以强度、倒箱量为目标,并遵循若干装卸规则,对挂靠多港口的集装箱船全航线配载问题提出一种全航线智能预配算法.
Azevedo等[10]针对集装箱船配载问题,提出6种装载规则和2种卸载规则.Benedito等[11]提出在混合Bay装载过程中,先卸载港后装载,后卸载港先装载的规则.利用以上这些规则,可以减小集装箱全航线配载问题的求解难度.
全航线智能预配算法的基本步骤如下.
步骤1 将集装箱船Bay位按自船艏至船艉进行编号,记作:BayID=1,2,…,m,其所包含的箱位数量分别为r1,r2,…,rm,距船舯的位置分别为x1,x2,…,xm.
步骤3 按上节所述0-1整数规划模型,采用混合整数规划算法或两种智能算法(遗传算法、蚁群算法)求解之,得到第1港装载结果.
在蚁群算法求解过程中,将距离函数定义为
(13)
其他诸如概率函数、信息素更新规则等的定义与基本蚁群算法一致,且采用蚁周模型进行更新[12].
步骤4 船舶航行至第2港,先清空卸载港编号为本港的集装箱,于其他港卸载的集装箱保持不变,卸载完成后,更新船舶Bay位属性,在第2港,箱子的拆分、重量的分配要视当前集装箱对于船舯的力矩而定,规定船舯往船艏为正方向,则如果当前力矩为正值,且 需要补充箱子的Bay位位置为负,则取同一卸载港重箱进行补充;反之,取同一卸载港轻箱补充.若补充后,剩余箱子数目小于被补充Bay位原有箱子数目,则不进行补充.补充完成后,按卸载港编号从大到小进行配载,对于数量不超过Bay位容量的,作为一个箱组进行配载,对于数量超过Bay位容量的,要对其进行拆分,拆分时,要不选择最轻箱进行拆分,要不选择最重箱进行拆分,视当前力矩值的正负及Bay位位置而定.当有多种Bay位可选时,调用混合整数规划算法或者智能算法求解之.如此往复,直到所有箱子都配载完毕,便得到第2港配载方案.
步骤5 对除目的港以外的其他港进行相同操作,并在目的港清空Bay位中的所有集装箱,得到整个全航线预配方案.
3 结果与分析
假设某集装箱船在某一航线上将要挂靠6个港口,该船上共有8个Bay位,均装TEU,相邻两Bay位之间的间距都为100 mm,每一Bay位的最大容量都为46箱.另一艘集装箱船同样在这一航线上挂靠6个港口,该船上共有40个Bay位,亦均装20英尺的标准箱,相邻两Bay位之间的间距都为100 mm,每一Bay位的最大容量都为200箱,箱子的重量有3种规格,即7,12和18 t.8 Bay集装箱船的装箱矩阵及与之对应的重量矩阵分别为

表2为三种算法对8 Bay集装箱船在第1港口装载后的求解结果比较.其中蚁群算法和遗传算法都计算100代.遗传算法中,交叉概率取0.75,变异率取0.25,种群数量取200,精英个体数取30.蚁群算法中,蚂蚁数量取5,信息素启发因子α取2,期望启发式因子β取3,信息素挥发系数ρ取0.3,信息素常量Q取1 000.并在同一台计算机上进行计算.
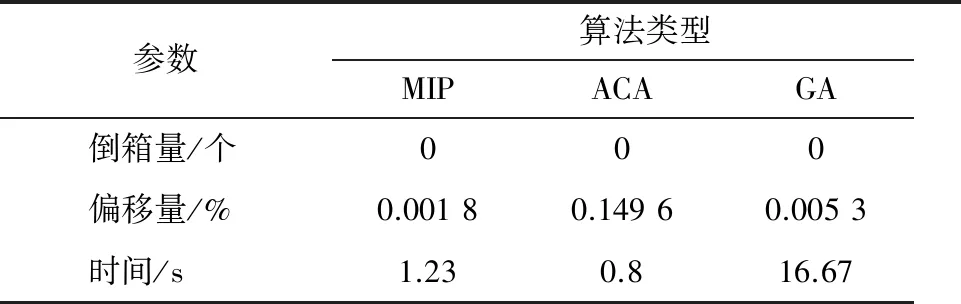
表2 不同算法的计算结果
模拟集装箱Bay位总长为49.164 m,在各港装载后的重心纵向偏移量见表3.按照第2部分的全航线智能预配算法,可得采用混合整数规划求解8Bay集装箱船的结果,见表4.

表3 重心纵向偏移量

表4 全航线预配结果
注:a(i,j,w)表示装载港为i,卸载港为j的集装箱数量为a,重量为w;a1(i,j,w1)+a2(k,q,w2)+…,表示混装Bay位,且按装载顺序相加.
4 结 束 语
本文针对挂靠多港口集装箱船的全航线预配问题,采用了基于规则的方式,以倒箱量最少、船舶纵向强度最优为目标,并结合三种算法即混合整数规划算法、蚁群算法和遗传算法,提出了针对该问题的智能预配算法.采用该算法,可以得到船舶在首港预配的最优解及后续港预配的近似最优解.模拟实验结果表明所提出的算法可行,为集装箱船舶的全航线多目标预配问题提供了一个可用的模型,为Bay位排箱(进一步优化稳性与横倾)奠定基础.并可为其他船舶的智能配载问题作参考。
[1]张维英.集装箱船全航线配载智能优化研究[D].大连:大连理工大学,2006.
[2]张维英,林焰,纪卓尚,等.集装箱船全航线Bay位排箱优化模型[J].上海交通大学学报,2007,41(2):199-204.
[3]张维英,林焰,纪卓尚,等.集装箱船全航线预配优化模型与算法研究[J].大连理工大学学报,2008,48(5):673-678.
[4]AMBROSINO D, SCIOMACHEN A, TANFANI E. A decomposition heuristics for the container ship stowage problem[J]. Journal of Heuristics,2006,12(3):211-233.
[5]AVRIEL M, PENN M, SHPIRER N. Container ship stowage problem: complexity and connection to the coloring of circle graphs[J]. Discrete Applied Mathematics,2000,103(1):271-279.
[7]PACINO D, DELGADO A, JENSEN R M, et al. Fast generation of near-optimal plans for eco-efficient stowage of large container vessels[C]∥ International Conference,2011(2):286-301.
[8]孙俊清,陈忱,刘凤连.考虑船舶稳定性的多港口集装箱配载问题[J].计算机工程与应用,2012,48(32):236-243.
[9]卫家骏.集装箱船智能配载研究[D].大连:大连海事大学,2012.
[10]AZEVEDO A T D, ARRUDA E F D, NETO L L D S, et al. Solution of the 3D stochastic stowage planning for container ships through representation by rules[C]∥ International Workshop on Knowledge Discovery, Knowledge Management and Decision Support,2013:120-129.
[11]BENEDITO M P L, SANTOS A G D. Evolutionary algorithm and ant colony optimization for a container stowage problem[J]. Discrete Applied Mathematics,2015(1):55-58.
[12]汪定伟.智能优化方法[M].北京:高等教育出版社,2007.
A Research on Intelligent Pre-stowage Planning Problem for Containerships in Full Routes
WANG Yuanyuan CHEN Shunhuai
(KeyLaboratoryofHighPerformanceShipTechnology,MinistryofEducation,Wuhan430063,China)
In order to solve the pre-planning problem for containerships in full routes using an intelligent way, a 0-1 integer programming for the problem is put forward by setting the number of shift and ship longitudinal bending moment value as goals. By the rule based methods, the problem is solved by the Mixed Integer Programming Algorithm (MIPA), Ant Colony Algorithm (ACA) and Genetic Algorithm (GA), respectively. It shows that when the scale of the problem is small, the MIPA is very efficient, and the optimal solution can be found by it. An intelligent algorithm for pre-planning problem of containerships in full routes based on the MIPA, ACA and GA is given, respectively. Finally, the pre-planning result of a containership with 8 bays is shown, it assures that the number of shift is zero, and the ship longitudinal bending moment value is considered as the objective, which means the longitudinal offsets of the center of gravity is minimized.
containerships; pre-stowage; integer programming; Genetic Algorithm; Ant Colony Algorithm
2017-06-15
U695.22
10.3963/j.issn.2095-3844.2017.04.034
汪圆圆(1992—):男,硕士生,主要研究领域为智能船舶
