静磁场任意分布电流的镜像源研究

谢宝昌

(上海交通大学 电子信息与电气工程学院， 上海 200240)

静磁场任意分布电流的镜像源研究

谢宝昌

(上海交通大学 电子信息与电气工程学院， 上海 200240)

“电磁场”教材给出了静磁场平行交界面无限长直载流导线的镜像结果。本文利用矢量磁位研究任意分布电流静磁场平面镜像问题，发现交界面衔接条件只能确定镜像场源的水平分量，而垂直分量需要根据电流连续性原理确定，并且垂直和平行于交界面电流密度分量的镜像结果不同，研究结果有助于学生对空间分布电流密度磁介质平面镜像方法的完整理解。

静磁场; 交界面条件; 镜像法; 矢量磁位

0 引言

“电磁场”教材给出了无限长直载流导线的平面磁介质镜像结果[1,2]，但实际问题中，电流不仅存在平行交界面分量，而且有垂直交界面分量。

本文针对静磁场任意电流密度平面镜像问题，利用电流连续性、矢量磁位及其交界面衔接条件确定镜像场源，使得静磁场平面镜像内容更加完整。

1 静磁场平面镜像问题

设以z=0为分界面，上、下两个半空间填充磁介质，磁导率分别为μ1和μ2，在上半空间有任意分布电流密度J，如图1(a)所示。

(a) (b) (c) 图1 磁介质平面镜像

2 镜像法求解矢量磁位

根据镜像法原理确定空间场量必须分区域求解。对于上半空间(z>0)的磁场，已知场源J(x0,y0,z0)，将下半空间磁介质参数改为μ1，并在镜像位置设置镜像电流密度J1(x0,y0, -z0)。对于下半空间(z<0)的磁场，将上半空间磁介质参数改为μ2，并在已知场源J(x0,y0,z0)位置增加镜像电流密度J2(x0,y0,z0)，自然这两个电流密度可以合成为一个电流密度。

利用矢量磁位求解场量比较方便，因静磁场磁感应强度B无散，引入矢量磁位A使得B=▽×A，并且根据库仑规范▽×A=0，得到矢量磁位满足泊松方程

▽2A=-μJ

(1)

以坐标原点为矢量磁位参考点，式(1)的解为

(2)

由此可知图1上、下半空间的矢量磁位分别为

(3a)

(3b)

其中，场点矢径r=axx+ayy+azz，源点矢径s=axx0+ayy0+azz0，镜像源点矢径s1=axx0+ayy0-azz0，V1为V的镜像区域，dV1为dV的镜像体元，即dV1=-dV，矢量磁位A1等式右边第二项体积分等同于区域V中的体积分。

3 矢量磁位满足的交界面条件

交界面条件是磁感应强度B法向分量连续，对应矢量磁位A切向分量连续，磁场强度H切向分量连续。因为H=B/μ=▽×A/μ，于是得到

az×A1(r0)=az×A2(r0)

(4a)

μ2az×▽×A1(r0)=μ1az×▽×A2(r0)

(4b)

其中，交界面上场点矢径r0=axx+ayy。

4 镜像场源的确定

考虑到镜像关系，由式(3a)和(3b)代入式(4a)得到矢量磁位切向分量连续满足的方程:

(5)

其中，源点矢径s平行平面分量s0=axx0+ayy0。

式(5)右边为常矢量，左边为r0的函数，则有

μ1(Jp+J1p)=μ2(Jp+J2p)

(6)

其中，平行于交界面的场源分量分别为Jp，J1p和J2p。

类似地，由式(3a)和(3b)代入式(4b)得到磁场强度切向分量连续时矢量磁位满足的方程:

(7)

化简后得到

(8)

其中，垂直于交界面的镜像场源分量分别为J1z和J2z。

根据电流连续性原理，电流密度J的散度为零

▽·J=▽·Jp+▽·Jz=0

(9)

式(9)中的电流密度也可以是镜像电流源，电流密度矢量线是闭合的，式(8)第二项利用分步积分对z0积分一次后并利用电流密度散度为零得到

(10)

将式(10)代入式(8)得到

(11)

由此可见，镜像场源平行于交界面的分量满足

J1p=-J2p

(12)

由式(6)和式(12)得到平行于交界面的镜像电流密度与给定电流密度分量的关系:

J1p=-J2p=kmJp

(13)

其中，km=(μ2-μ1)/(μ2+μ1)。

由式(9)和(13)得到垂直于交界面的镜像电流密度与给定电流密度分量的偏导数关系

(14a)

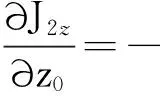
(14b)

于是，垂直于交界面的镜像场源与给定电流密度分量满足：J1z=J2z=-kmJz

(15)(谢宝昌文)

由式(13)和(15)得到镜像电流密度与给定电流密度的关系:

J1(s1)=km[Jp(s)-Jz(s)]，z0>0

(16a)

J2(s)=-kmJ(s)，z0>0

(16b)

5 结语

本文对静磁场任意电流分布的镜像问题进行了研究，结果表明仅仅依靠交界面条件只能确定平行镜像电流分量，垂直镜像电流分量需要根据电流连续性原理确定，而且还发现垂直和平行于交界面电流密度分量的镜像结果不同。本研究有助于学生对空间分布电流密度磁介质平面镜像方法的完整理解。

[1] 周希朗. 电磁场[M]. 北京：机械工业出版社，2014年

[2] 谢宝昌. 电磁能量[M]. 北京：机械工业出版社，2016年

Research on Mirror Image Source of Arbitrary Current Density in Magneto-static Field

XIE Bao-chang

(SchoolofElectronicInformationandElectricalEngineering,ShanghaiJiaoTongUniversity,Shanghai200240,China)

Mirror image source of infinitive long current line with respect to planar interface is given in textbook of Electromagnetic Field. The problem of arbitrary current density distribution is investigated based on magnetic vector potential in this paper. Only horizontal components of the mirror image sources can be determined by boundary conditions while for the vertical components we must adopt the principle of current continuity. Furthermore, the difference between perpendicular and parallel component is found in the results, which is helpful for student to wholly understand the mirror image method of magnetic media planar interface.

magneto-static field; boundary conditions; mirror image method; magnetic vector potential

2016-06-28;

2016-09- 22

谢宝昌(1965-)，男，博士，副教授，主要从事电机与电器的教学与研究工作，Email：bcxie@sjtu.edu.cn

TM153

A

1008-0686(2017)04-0034-03