浅析“绳、杆速度牵连模型”

宋海峰

(江苏省天一中学，江苏 无锡 214101)

浅析“绳、杆速度牵连模型”

宋海峰

(江苏省天一中学，江苏 无锡 214101)

图1

“绳、杆速度牵连模型”是高中物理教学中的一个难点,也是各高校自主招生和竞赛出题的热点．对一些简单的、常见的“绳、杆速度牵连模型”,学生由于平时的反复训练基本能应付外,对一些稍微复杂、陌生的“绳、杆速度牵连模型”,学生在处理时就常常会思维混乱进而无从下手．究其原因,就是学生对此类问题只会生搬硬套,知其然而不知其所以然．笔者在辅导学生自主招生时布置了一道相关习题,根据学生的作业反馈谈谈此类问题常见错误及原因和一般处理的方法．

1 题目

图2

如图1所示,两只小环O和O′分别套在静止不动的竖直杆AB和A′B′上,一根不可伸长的绳子一端系在A′点上,穿过环O′,另一端系在环O上．若环O′以恒定速度v′向下运动,当∠AOO′=α时,求环O的速度v?

2 常见错误及原因分析

常见错误1.环O′以v′向下运动,绳子O′A′以v′向上运动,绳子不可伸长,则绳子O′O以v′斜向上运动,再将v′分解到竖直方向和水平方向,如图2所示,则v′在竖直方向上的分量就是环O的速度,即v=v′cosα.

原因分析：造成上述错误的原因,就是没有分清合运动与分运动的概念,错误地认为绳子O′O的速度v′就是环O的合速度(合运动),因此将v′直接进行分解．这里涉及合运动的概念,何为合运动?物体实际的运动就是合运动．显然,环O由于杆AB的约束,实际竖直向上运动,这个运动才是合运动,将这个合速度按效果沿绳子和垂直绳子分解才合理．

图3

常见错误2.如图3所示,把环O和环O′的速度分解,然后根据速度关联问题中的结论“刚性绳、杆上各点在同一时刻具有相同的沿绳、沿杆的分速度”,即v′cosα=vcosα,得v=v′．

原因分析：此种解法虽然分清了合运动和分运动的概念,抓住了环O、环O′的合运动,但生搬硬套速度关联问题中“刚性绳、杆上各点在同一时刻具有相同的沿绳、沿杆的分速度”的结论,而未注意到将环O、环O′速度分解后两分速度方向相反,即相向运动,其效果是使绳子缩短,它们根本不可能相等．所以在使用一些有用结论的同时,要注意知识迁移的条件,避免出现表面类似但本质不同的知识之间,在迁移过程中产生相互干扰和破坏,即产生负迁移．

3 正确的解法

方法1.微元法.

设经过时间Δt,环O、环O′前进的位移分别为

图4

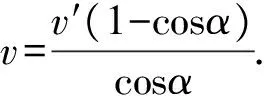
点评:使用微元法时可设想物体发生一个微小位移,分析由此引起的牵连物体的位移,再找到位移间的关系,进而求出牵连物体间速度的关系．微元法是分析、解决物理问题的常用方法,它贯穿于高中物理知识体系．作为大学知识在高中物理中的应用,“微元法”不但可以丰富学生处理问题的方法,而且可以拓展学生的思维．对于高三的学生特别是要参加自主招生的学生,应当熟练掌握．教师在平时的教学中可以不断向学生渗透,潜移默化,优化学生的思维品质．

方法2.速度分解法.

类比:如图5所示,甲车用绳子通过定滑轮以不变的速度v1拉水平面上的乙车,当绳与水平方向成α角时,求乙车的速度v2?

图5

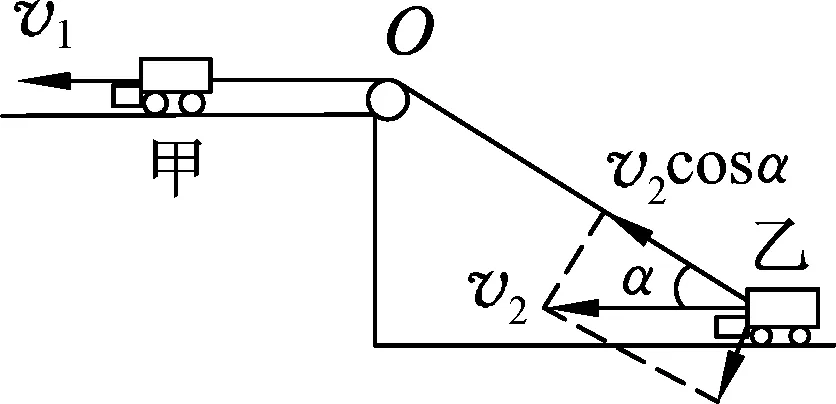
图6

图7

基于“绳子不能伸缩”,绳子上各点的速率应该相等,甲车运动的速率就是绳子运动的速率,而乙车的实际速度为v2,方向水平向左,将其沿绳子和垂直绳子分解,如图6所示,则v1=v2cosα.

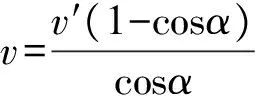
点评:使用速度分解法的前提是正确判断研究对象的合运动(实际运动),分析清楚分运动产生的实际意义和效果,这一点是解答问题的关键．此方法中,笔者灵活选取环O′为参考系,采用类比法将复杂的、陌生的情景转化为学生熟悉的情景,使所求问题简单化,易于学生理解和接受,从而起到帮助学生巩固知识、加深认识和提高能力的作用．教师在平时的教学中要注重引导学生通过联想、类比等方法,找出新旧事物在认知结构中共同的本质东西,充分利用迁移规律,由已知悟出未知,举一反三、触类旁通地去分析解决问题,从而提升学生的核心素养．

方法3.应用能量转化及守恒定律.

图8

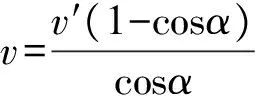
点评:显然这种方法不仅计算简单而且学生也易于理解,但处理此类问题时要注意不能直接计算绳子对两个环做的功,因为功是一个过程量,而题目要求的速度是一个瞬时量,所以我们可以转化为绳子做功的瞬时功率为0来处理,同时也要注意使用瞬时功率公式P=Fvcosα时不能忘了夹角．

思维是世界最美丽的火花,教师在教学中要结合解题突出学生创新思维的训练,不仅可使学生的“学”时刻保持机敏状态,激发求知、求异、求新的兴趣,而且换个角度,换个思维,或许暂时的困顿就柳暗花明了．

2017-02-13)